Deck 9: Nonlinear Differential Equations and Stability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/76
Play
Full screen (f)
Deck 9: Nonlinear Differential Equations and Stability
1
Consider the linear system 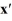 =
= 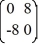 x.
x.
Identify all the eigenvalues.
A) = -8i
B) = 8
C) = -8
D) = 8i
E) = 0
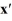 =
= 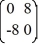 x.
x.Identify all the eigenvalues.
A) = -8i
B) = 8
C) = -8
D) = 8i
E) = 0
= -8i
= 8i
= 8i
2
Consider the linear system 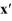 =
= 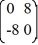 x.
x.
The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source
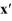 =
= 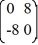 x.
x.The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source
center
3
Consider the linear system 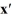 =
= 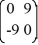 x.
x.
The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable
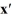 =
= 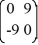 x.
x.The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable
a stable
4
Consider the linear system 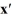 =
= 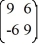 x.
x.
Identify all the eigenvalues.
A) = -15i
B) = 3i
C) = 15i
D) = -6i
E) = 6i
F) = -3i
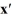 =
= 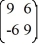 x.
x.Identify all the eigenvalues.
A) = -15i
B) = 3i
C) = 15i
D) = -6i
E) = 6i
F) = -3i

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
5
Consider the linear system 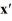 =
= 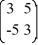 x.
x.
The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source
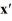 =
= 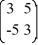 x.
x.The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
6
Consider the linear system 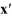 =
= 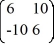 x.
x.
The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable
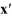 =
= 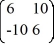 x.
x.The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
7
Consider the linear system 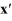 =
= 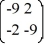 x.
x.
Identify all the eigenvalues.
A) = 7i
B) = -11i
C) = -7i
D) = -2i
E) = 11i
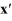 =
= 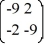 x.
x.Identify all the eigenvalues.
A) = 7i
B) = -11i
C) = -7i
D) = -2i
E) = 11i

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
8
Consider the linear system 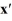 =
= 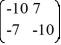 x.
x.
The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source
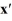 =
= 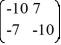 x.
x.The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
9
Consider the linear system 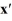 =
= 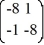 x.
x.
The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable
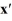 =
= 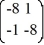 x.
x.The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
10
Consider the linear system 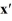 =
= 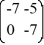 x.
x.
Identify all of the eigenvalues.
A) = -7
B) = 7
C) = 0
D) = 5
E) = -5
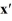 =
= 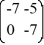 x.
x.Identify all of the eigenvalues.
A) = -7
B) = 7
C) = 0
D) = 5
E) = -5

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
11
Consider the linear system 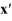 =
= 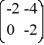 x.
x.
Identify which two of the following are fundamental solution vectors for this system.
A)
B)
C)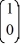
D)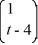
E)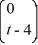
F)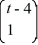
 =
= 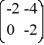 x.
x.Identify which two of the following are fundamental solution vectors for this system.
A)

B)

C)
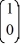
D)
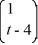
E)
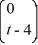
F)
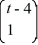

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
12
Consider the linear system 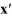 =
= 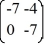 x.
x.
The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source
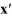 =
= 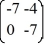 x.
x.The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
13
Consider the linear system 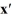 =
= 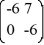 x.
x.
The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable
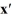 =
= 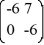 x.
x.The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
14
Consider the linear system 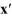 =
= 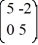 x.
x.
Identify all of the eigenvalues.
A) = 5
B) = -5
C) = 0
D) = 2
E) = -2
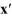 =
= 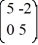 x.
x.Identify all of the eigenvalues.
A) = 5
B) = -5
C) = 0
D) = 2
E) = -2

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
15
Consider the linear system 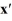 =
= 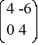 x.
x.
Identify which two of the following are fundamental solution vectors for this system.
A)
B)
C)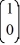
D)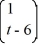
E)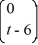
F)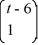
 =
= 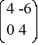 x.
x.Identify which two of the following are fundamental solution vectors for this system.
A)

B)

C)
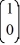
D)
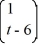
E)
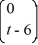
F)
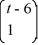

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
16
Consider the linear system 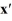 =
= 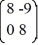 x.
x.
The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source
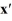 =
=  x.
x.The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
17
Consider the linear system 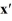 =
= 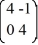 x.
x.
The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable
 =
= 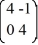 x.
x.The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
18
Consider the linear system 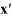 =
= 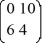 x.
x.
Identify all of the eigenvalues.
A) = -6
B) = -10
C) = 0
D) = 10
E) = 6
 =
= 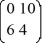 x.
x.Identify all of the eigenvalues.
A) = -6
B) = -10
C) = 0
D) = 10
E) = 6

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
19
Consider the linear system 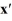 =
= 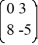 x.
x.
The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source
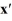 =
= 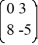 x.
x.The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
20
Consider the linear system 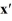 =
= 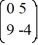 x.
x.
The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable
 =
= 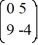 x.
x.The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
21
Consider the linear system 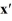 =
= 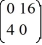 x.
x.
Identify all of the eigenvalues.
A) = -8
B) = -4
C) = 0
D) = -16
E) = 4
F) = 16
G) = 8
 =
= 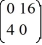 x.
x.Identify all of the eigenvalues.
A) = -8
B) = -4
C) = 0
D) = -16
E) = 4
F) = 16
G) = 8

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
22
Consider the linear system 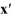 =
= 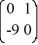 x.
x.
The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source
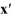 =
= 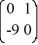 x.
x.The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
23
Consider the linear system 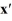 =
= 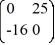 x.
x.
The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable
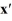 =
= 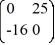 x.
x.The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
24
Consider the linear system 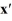 =
= 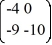 x.
x.
Identify all of the eigenvalues.
A) = -4
B) = 4
C) = 0
D) = -9
E) = 9
F) = -10
G) = 10
 =
= 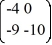 x.
x.Identify all of the eigenvalues.
A) = -4
B) = 4
C) = 0
D) = -9
E) = 9
F) = -10
G) = 10

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
25
Consider the linear system 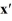 =
= 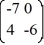 x.
x.
The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source
 =
= 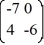 x.
x.The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
26
Consider the linear system 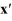 =
= 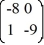 x.
x.
The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable
 =
= 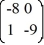 x.
x.The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the linear system 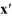 =
= 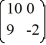 x.
x.
Identify all of the eigenvalues.
A) = 10
B) = -10
C) = 0
D) = -9
E) = 9
F) = -2
G) = 2
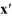 =
= 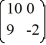 x.
x.Identify all of the eigenvalues.
A) = 10
B) = -10
C) = 0
D) = -9
E) = 9
F) = -2
G) = 2

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
28
Consider the linear system 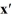 =
= 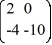 x.
x.
The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source
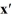 =
= 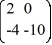 x.
x.The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
29
Consider the linear system 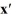 =
= 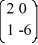 x.
x.
The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable
 =
= 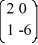 x.
x.The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
30
Consider the linear system 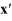 =
= 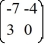 x.
x.
Identify all of the eigenvalues.
A) = 0
B) = 4
C) = -4
D) = 3
E) = -3
 =
= 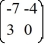 x.
x.Identify all of the eigenvalues.
A) = 0
B) = 4
C) = -4
D) = 3
E) = -3

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
31
Consider the linear system  =
= 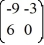 x.
x.
The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source
 =
= 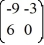 x.
x.The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
32
Consider the linear system 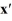 =
= 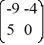 x.
x.
The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable
 =
= 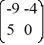 x.
x.The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
33
Consider the linear system 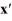 =
= 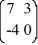 x.
x.
Identify all of the eigenvalues.
A) = 0
B) = -3
C) = 3
D) = -4
E) = 4
 =
= 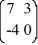 x.
x.Identify all of the eigenvalues.
A) = 0
B) = -3
C) = 3
D) = -4
E) = 4

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
34
Consider the linear system 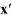 =
= 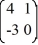 x.
x.
The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source
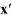 =
= 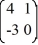 x.
x.The origin is a ________.
A) spiral sink
B) center
C) spiral source
D) nodal sink
E) saddle point
F) degenerate node
G) nodal source

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
35
Consider the linear system 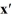 =
= 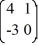 x.
x.
The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable
 =
= 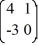 x.
x.The origin is ________ critical point.
A) a stable
B) an unstable
C) an asymptotically stable

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
36
For which of the following systems is the origin a saddle point?
A)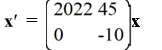
B)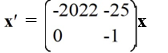
C)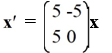
D)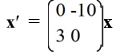
A)
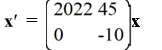
B)
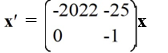
C)
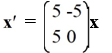
D)
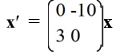

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
37
The trajectories of some nonzero solutions of this system converge to the origin as t while many other solutions do not.
A)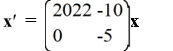
B)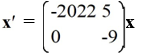
C)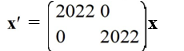
D)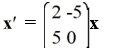
E)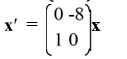
A)
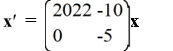
B)
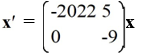
C)
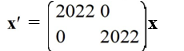
D)
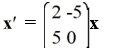
E)
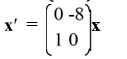

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
38
Every nonzero solution of this system spirals away from the origin.
A)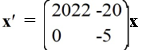
B)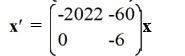
C)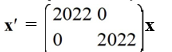
D)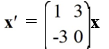
E)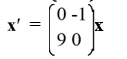
A)
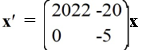
B)
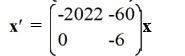
C)
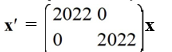
D)
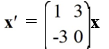
E)
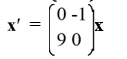

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
39
For which of the following systems do all solution trajectories converge to the origin as t ?
A)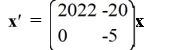
B)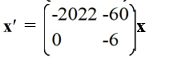
C)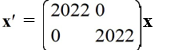
D)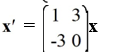
E)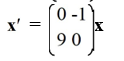
A)
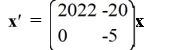
B)
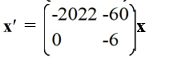
C)
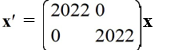
D)
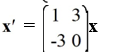
E)
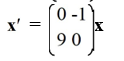

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
40
For which of the following systems is the origin a degenerate node?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
41
For which of the following systems is every solution periodic?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
42
Which of the following is a critical point of this nonlinear system?
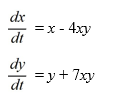
Select all that apply.
A) (7, -4)
B) (-7, 4)
C)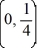
D) (0, 0)
E)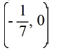
F)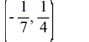
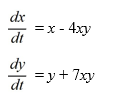
Select all that apply.
A) (7, -4)
B) (-7, 4)
C)

D) (0, 0)
E)
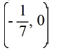
F)
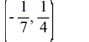

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
43
Which of the following is a critical point of this nonlinear system?
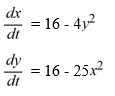
Select all that apply.
A)
B)
C)
D)
E)
F)
G)
H)
I)
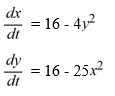
Select all that apply.
A)
B)
C)
D)
E)
F)
G)
H)
I)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
44
Which of the following is a critical point of this nonlinear system?
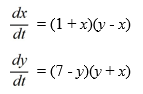
Select all that apply.
A) (1, -1)
B) (-7, -7)
C) (1, 7)
D) (-1, 1)
E) (-1, 7)
F) (-7, 7)
G) (7, 7)
H) (0, 0)
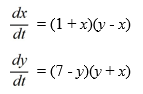
Select all that apply.
A) (1, -1)
B) (-7, -7)
C) (1, 7)
D) (-1, 1)
E) (-1, 7)
F) (-7, 7)
G) (7, 7)
H) (0, 0)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
45
Find an equation of the form H(x, y) = C, where C is an arbitrary real constant, satisfied by the trajectories of the following nonlinear system:
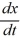 = 6y
= 6y
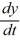 = -10 x
= -10 x
A)
B)
C)
D)
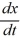 = 6y
= 6y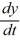 = -10 x
= -10 xA)
B)
C)
D)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
46
Find an equation of the form H(x, y) = C, where C is an arbitrary real constant, satisfied by the trajectories of the following nonlinear system:
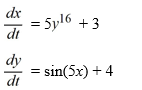
A)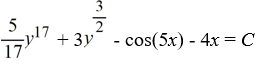
B)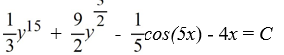
C)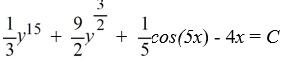
D)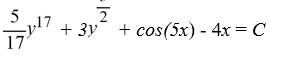
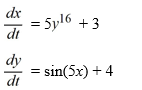
A)
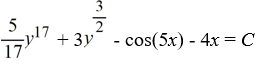
B)
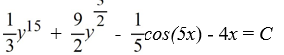
C)
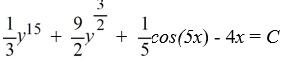
D)
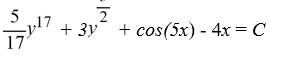

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
47
Consider the following nonlinear system:
 =
= 
 +
+ 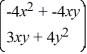
Let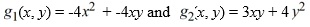 Express x and y using polar coordinates and determine which of these statements is true.
Express x and y using polar coordinates and determine which of these statements is true.
A) The system is locally linear near the origin.
B) The system is not locally linear near the origin because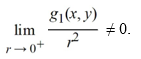
C) The system is not locally linear near the origin because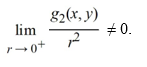
D) The origin is not an isolated critical point.
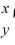 =
= 
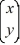 +
+ 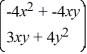
Let
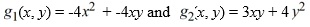 Express x and y using polar coordinates and determine which of these statements is true.
Express x and y using polar coordinates and determine which of these statements is true.A) The system is locally linear near the origin.
B) The system is not locally linear near the origin because
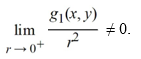
C) The system is not locally linear near the origin because
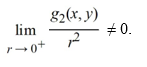
D) The origin is not an isolated critical point.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
48
Consider the following nonlinear system:
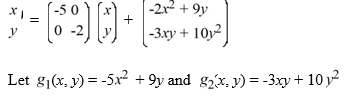
Express x and y using polar coordinates and determine which of these statements is true.
A) The system is locally linear near the origin.
B) The system is not locally linear near the origin because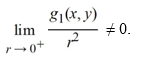
C) The system is not locally linear near the origin because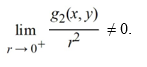 .
.
D) The origin is not an isolated critical point.
E) Both B and C.
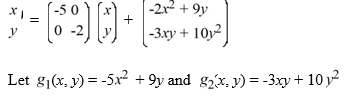
Express x and y using polar coordinates and determine which of these statements is true.
A) The system is locally linear near the origin.
B) The system is not locally linear near the origin because
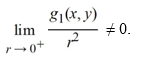
C) The system is not locally linear near the origin because
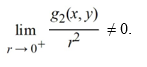 .
.D) The origin is not an isolated critical point.
E) Both B and C.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
49
Consider the following nonlinear system:
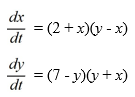
Which of the following is a critical point of this nonlinear system? Select all that apply.
A) (2, -2)
B) (-7, -7)
C) (2, 7)
D) (-2, 2)
E) (-2, 7)
F) (-7, 7)
G) (7, 7)
H) (0, 0)
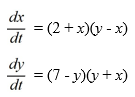
Which of the following is a critical point of this nonlinear system? Select all that apply.
A) (2, -2)
B) (-7, -7)
C) (2, 7)
D) (-2, 2)
E) (-2, 7)
F) (-7, 7)
G) (7, 7)
H) (0, 0)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
50
Consider the following nonlinear system:



Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
51
Consider the following nonlinear system:
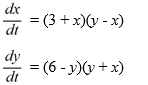
Which of the following statements are true? Select all that apply.
A) (-3, 3) is an asymptotically stable node.
B) (3, -3) is an unstable spiral node.
C) (-3, 3) is an unstable node.
D) (6, 6) is an unstable node.
E) (6, -6) is an unstable node.
F) (6, 6) is an asymptotically stable node.
G) (0, 0) is a saddle point.
H) (-6, -6) is an asymptotically stable node.
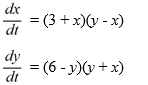
Which of the following statements are true? Select all that apply.
A) (-3, 3) is an asymptotically stable node.
B) (3, -3) is an unstable spiral node.
C) (-3, 3) is an unstable node.
D) (6, 6) is an unstable node.
E) (6, -6) is an unstable node.
F) (6, 6) is an asymptotically stable node.
G) (0, 0) is a saddle point.
H) (-6, -6) is an asymptotically stable node.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
52
Consider the following nonlinear system:
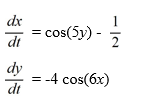
Which of the following is a complete list of the critical points of this nonlinear system?
A)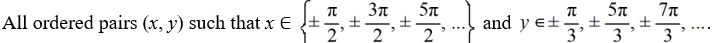
B)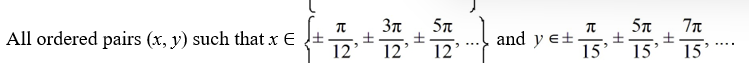
C)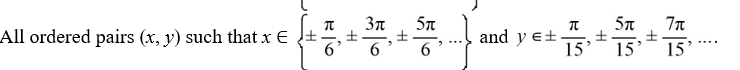
D)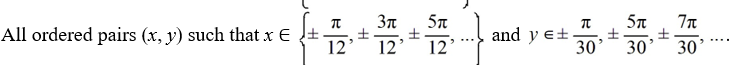
E)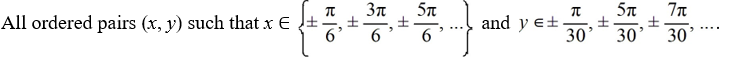
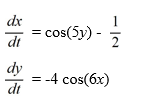
Which of the following is a complete list of the critical points of this nonlinear system?
A)
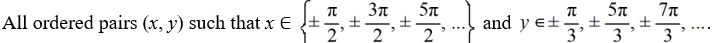
B)
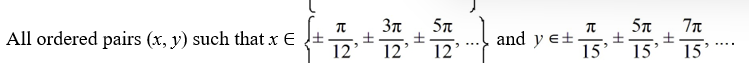
C)
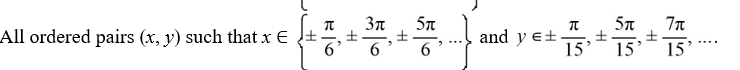
D)
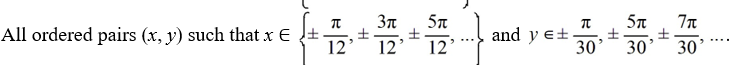
E)
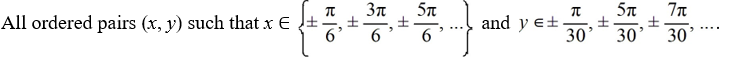

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
53
Consider the following nonlinear system:
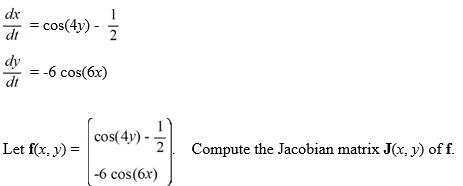
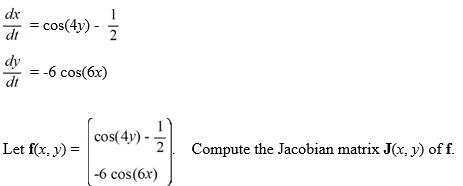

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
54
Consider the following nonlinear system:
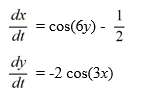
Which of the following statements are true? Select all that apply.
A) is an unstable saddle point.
B) is a stable center.
C) is a stable center.
D) is an asymptotically stable spiral point.
E) is an improper node.
F) is a stable center.
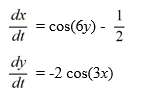
Which of the following statements are true? Select all that apply.
A) is an unstable saddle point.
B) is a stable center.
C) is a stable center.
D) is an asymptotically stable spiral point.
E) is an improper node.
F) is a stable center.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
55
Consider the following nonlinear system:
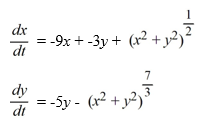
Which of the following statements is true?
A) The origin is an unstable spiral point.
B) The origin is an asymptotically stable node.
C) The origin is an asymptotically stable spiral point.
D) The origin is a stable sink.
E) The origin is a stable improper node.
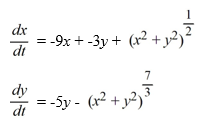
Which of the following statements is true?
A) The origin is an unstable spiral point.
B) The origin is an asymptotically stable node.
C) The origin is an asymptotically stable spiral point.
D) The origin is a stable sink.
E) The origin is a stable improper node.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
56
Consider this competing species model:
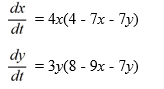
Which of these are critical points for this system? Select all that apply.
A)
B)
C)
D)
E)
F)
G)
H)
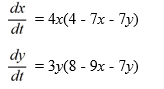
Which of these are critical points for this system? Select all that apply.
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
57
Consider this competing species model:
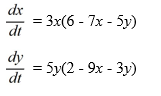
Which of the following statements are true? Select all that apply.
A) The entire first quadrant is the basin of attraction for the critical point .
B) The origin is an unstable node.
C) Both and are saddle points.
D) Both and are saddle points
E) All solution trajectories approach the origin as .
F) The critical point corresponds to coexistence in this model.
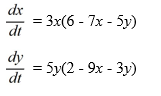
Which of the following statements are true? Select all that apply.
A) The entire first quadrant is the basin of attraction for the critical point .
B) The origin is an unstable node.
C) Both and are saddle points.
D) Both and are saddle points
E) All solution trajectories approach the origin as .
F) The critical point corresponds to coexistence in this model.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
58
Suppose ? is a real parameter. Consider this competing species model:
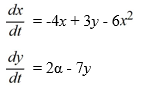
Which of these are true? Select all that apply.
A) The origin is a critical point of this system for all values of .
B) The -nullcline is the curve .
C) The -nullcline is the horizontal line .
D) The system has no critical points for values of
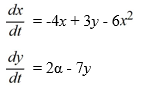
Which of these are true? Select all that apply.
A) The origin is a critical point of this system for all values of .
B) The -nullcline is the curve .
C) The -nullcline is the horizontal line .
D) The system has no critical points for values of

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
59
Suppose ? is a positive real parameter. Consider this competing species model:
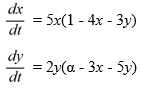
What are the nullclines for this system?
A) x = 0
B) y = 0
C)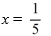
D) 4x + 3y = 1
E)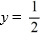
F)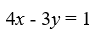
G)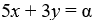
H)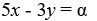
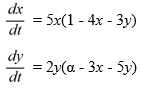
What are the nullclines for this system?
A) x = 0
B) y = 0
C)
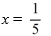
D) 4x + 3y = 1
E)
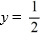
F)
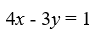
G)
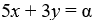
H)
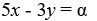

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
60
Suppose ? is a positive real parameter. Consider this competing species model:
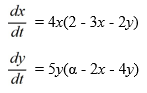
Which of these are critical points for this system? Select all that apply.
A)
B)
C)
D)
E)
F)
G)
H)
I)
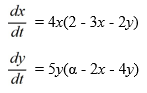
Which of these are critical points for this system? Select all that apply.
A)
B)
C)
D)
E)
F)
G)
H)
I)

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
61
Suppose α is a positive real parameter. Consider this competing species model:



Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
62
Suppose ? is a positive real parameter. Consider this competing species model:
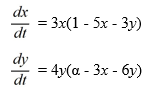
Which of the following statements is true?
A) The origin is an unstable node.
B) The origin is an unstable saddle point.
C) The origin is an asymptotically stable node.
D) The origin is a stable center.
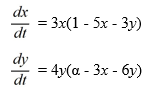
Which of the following statements is true?
A) The origin is an unstable node.
B) The origin is an unstable saddle point.
C) The origin is an asymptotically stable node.
D) The origin is a stable center.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
63
Consider the following Lotka-Volterra system of equations:
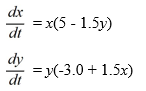
Determine all critical points for this system.
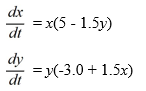
Determine all critical points for this system.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
64
Consider the following Lotka-Volterra system of equations:



Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
65
Consider the following Lotka-Volterra system of equations:
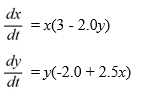
Which of these statements are true? Select all that apply.
A) The solution trajectories all spiral away from the point as
B) The solution trajectories are closed curves encircling the point .
C) The point is an unstable node.
D) The predator and prey populations exhibit a cyclic variation.
E) The origin is a saddle point.
F) The period of the solution trajectories is
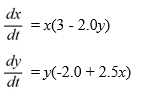
Which of these statements are true? Select all that apply.
A) The solution trajectories all spiral away from the point as
B) The solution trajectories are closed curves encircling the point .
C) The point is an unstable node.
D) The predator and prey populations exhibit a cyclic variation.
E) The origin is a saddle point.
F) The period of the solution trajectories is

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
66
Consider the function V(x, y) = 7 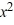 + xy + 5
+ xy + 5 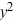 , where is a real number.Which of these statements is true?
, where is a real number.Which of these statements is true?
A) V(x, y) is negative definite, for every nonzero real number .
B) V(x, y) is positive definite, for every nonzero real number .
C) V(x, y) is negative definite, for every real number for which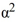 > 140.
> 140.
D) V(x, y) is positive definite, for every real number for which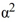 < 140.
< 140.
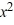 + xy + 5
+ xy + 5 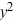 , where is a real number.Which of these statements is true?
, where is a real number.Which of these statements is true?A) V(x, y) is negative definite, for every nonzero real number .
B) V(x, y) is positive definite, for every nonzero real number .
C) V(x, y) is negative definite, for every real number for which
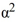 > 140.
> 140.D) V(x, y) is positive definite, for every real number for which
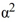 < 140.
< 140.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
67
Consider the following nonlinear system:
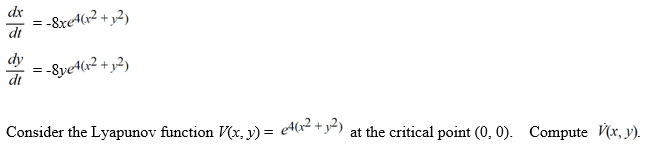
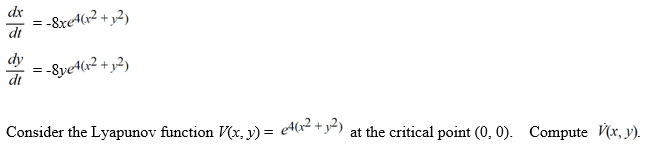

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
68
Consider the following nonlinear system:
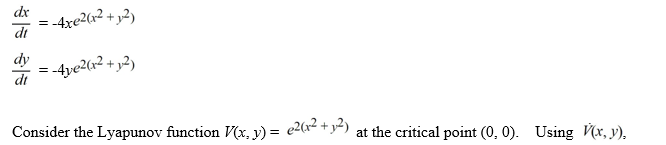
What can you conclude about this nonlinear system?
A) The origin is asymptotically stable.
B) The origin is an unstable node.
C) The basin of attraction for the origin is the entire xy-plane.
D) The origin is a center and all solution trajectories encircle it.
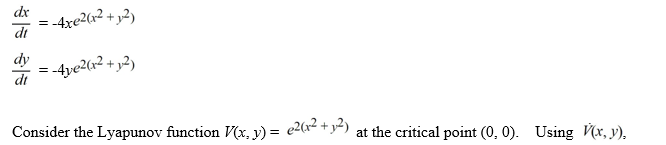
What can you conclude about this nonlinear system?
A) The origin is asymptotically stable.
B) The origin is an unstable node.
C) The basin of attraction for the origin is the entire xy-plane.
D) The origin is a center and all solution trajectories encircle it.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
69
Consider the following nonlinear system:
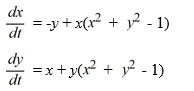
Convert this system into an equivalent system in polar form.
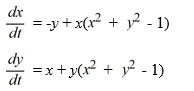
Convert this system into an equivalent system in polar form.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
70
Consider the following nonlinear system:
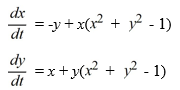
Which of these statements is true? Select all that apply.
A) There are no isolated closed trajectories for this system.
B) For r > 0, the corresponding solution trajectories spiral outward away from r = 1 in a counterclockwise fashion.
C) For 0 < r < 1, the corresponding solution trajectories spiral toward the origin in a counterclockwise fashion.
D) The unit circle is a semistable limit cycle.
E) The unit circle is an unstable limit cycle.
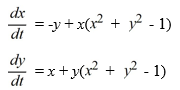
Which of these statements is true? Select all that apply.
A) There are no isolated closed trajectories for this system.
B) For r > 0, the corresponding solution trajectories spiral outward away from r = 1 in a counterclockwise fashion.
C) For 0 < r < 1, the corresponding solution trajectories spiral toward the origin in a counterclockwise fashion.
D) The unit circle is a semistable limit cycle.
E) The unit circle is an unstable limit cycle.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
71
Consider the following nonlinear system expressed in polar form:
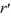 = r( r - 2)( r - 8)
= r( r - 2)( r - 8)
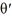 = 1
= 1
Which of these statements is true? Select all that apply.
A) r = 8 is a semistable limit cycle.
B) r = 2 is an asymptotically stable limit cycle.
C) For 2 < r < 8, the corresponding solution trajectories spiral outward away from r = 2 in a clockwise fashion.
D) For 0 < r < 2, the corresponding solution trajectories spiral toward the origin in a clockwise fashion.
E) For r > 8, the corresponding solution trajectories spiral outward away from r = 8 in a counterclockwise fashion.
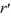 = r( r - 2)( r - 8)
= r( r - 2)( r - 8)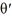 = 1
= 1Which of these statements is true? Select all that apply.
A) r = 8 is a semistable limit cycle.
B) r = 2 is an asymptotically stable limit cycle.
C) For 2 < r < 8, the corresponding solution trajectories spiral outward away from r = 2 in a clockwise fashion.
D) For 0 < r < 2, the corresponding solution trajectories spiral toward the origin in a clockwise fashion.
E) For r > 8, the corresponding solution trajectories spiral outward away from r = 8 in a counterclockwise fashion.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
72
Consider the following nonlinear system expressed in polar form: 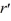 = r
= r 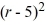 ( r - 7)
( r - 7)
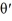 = -1
= -1
Which of these statements is true? Select all that apply.
A) All solution trajectories approach either r = 5 or r = 7 in a counterclockwise fashion.
B) r = 5 is a semistable limit cycle.
C) r = 7 is an unstable limit cycle.
D) For 0 < r < 5, the corresponding solution trajectories spiral toward r = 5 in a clockwise fashion.
E) For r > 7, the corresponding solution trajectories spiral outward away from r = 7 in a counterclockwise fashion.
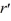 = r
= r 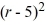 ( r - 7)
( r - 7)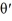 = -1
= -1Which of these statements is true? Select all that apply.
A) All solution trajectories approach either r = 5 or r = 7 in a counterclockwise fashion.
B) r = 5 is a semistable limit cycle.
C) r = 7 is an unstable limit cycle.
D) For 0 < r < 5, the corresponding solution trajectories spiral toward r = 5 in a clockwise fashion.
E) For r > 7, the corresponding solution trajectories spiral outward away from r = 7 in a counterclockwise fashion.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
73
Consider the van der Pol equation 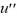 - 2.8(1 -
- 2.8(1 - 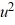 )
) 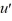 + u = 0.Write this equation as a nonlinear system in x and y, where x = u and y =
+ u = 0.Write this equation as a nonlinear system in x and y, where x = u and y = 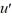 .
.
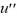 - 2.8(1 -
- 2.8(1 - 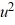 )
) 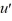 + u = 0.Write this equation as a nonlinear system in x and y, where x = u and y =
+ u = 0.Write this equation as a nonlinear system in x and y, where x = u and y = 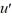 .
.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
74
Consider the van der Pol equation 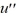 - 4.2(1 -
- 4.2(1 - 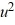 )
) 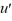 + u = 0.
+ u = 0.
The origin is an unstable node.
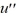 - 4.2(1 -
- 4.2(1 - 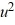 )
) 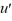 + u = 0.
+ u = 0.The origin is an unstable node.

Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
75
Consider the van der Pol equation 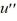 - 3.6(1 -
- 3.6(1 - 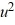 )
) 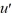 + u = 0.If a closed trajectory exists, it must encircle the origin.
+ u = 0.If a closed trajectory exists, it must encircle the origin.
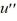 - 3.6(1 -
- 3.6(1 - 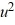 )
) 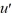 + u = 0.If a closed trajectory exists, it must encircle the origin.
+ u = 0.If a closed trajectory exists, it must encircle the origin.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck
76
Consider the van der Pol equation 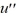 - 2.4(1 -
- 2.4(1 - 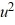 )
) 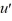 + u = 0.If a closed trajectory exists, then it must be contained within the vertical strip |x| < 1.
+ u = 0.If a closed trajectory exists, then it must be contained within the vertical strip |x| < 1.
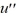 - 2.4(1 -
- 2.4(1 - 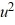 )
) 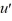 + u = 0.If a closed trajectory exists, then it must be contained within the vertical strip |x| < 1.
+ u = 0.If a closed trajectory exists, then it must be contained within the vertical strip |x| < 1.
Unlock Deck
Unlock for access to all 76 flashcards in this deck.
Unlock Deck
k this deck


