Deck 8: Numerical Methods
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/63
Play
Full screen (f)
Deck 8: Numerical Methods
1
The velocity (measured in meters per second) of an air-dropped container of food and supplies affixed to a parachute is described by the function v(t) = 66.8 tanh(0.20t), t 2.4, where t is measured in seconds. You are interested in approximating the vertical distance s(t) traveled by the package by time t = 2.50 seconds.Using a step size of h = 0.10 seconds, compute the vertical distance traveled in the first 2.50 seconds.
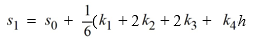
K1= ________
A) 66.8 tanh(0.20)
B) 66.8 tanh(0.20 × 2.4)
C)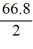 tanh(0.20 × 2.4)
tanh(0.20 × 2.4)
D)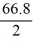 tanh
tanh 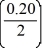
E) 66.8 tanh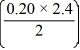
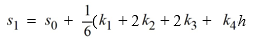
K1= ________
A) 66.8 tanh(0.20)
B) 66.8 tanh(0.20 × 2.4)
C)
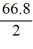 tanh(0.20 × 2.4)
tanh(0.20 × 2.4)D)
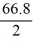 tanh
tanh 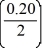
E) 66.8 tanh
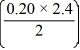
66.8 tanh(0.20 × 2.4)
2
The velocity (measured in meters per second) of an air-dropped container of food and supplies affixed to a parachute is described by the function v(t) = 57.2 tanh(0.12t), t 3.0, where t is measured in seconds. You are interested in approximating the vertical distance s(t) traveled by the package by time t = 3.05 seconds.Using a step size of h = 0.05 seconds, compute the vertical distance traveled in the first 3.05 seconds.
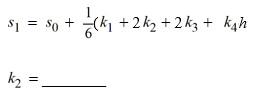
A) 57.2 tanh(0.12 × (3.0 + 0.05))
B) 57.2 tanh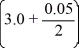
C)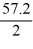 tanh(3.0 + 0.05)
tanh(3.0 + 0.05)
D) 57.2 tanh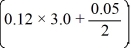
E)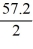 tanh
tanh 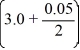
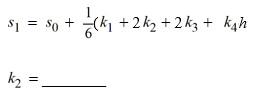
A) 57.2 tanh(0.12 × (3.0 + 0.05))
B) 57.2 tanh
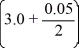
C)
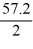 tanh(3.0 + 0.05)
tanh(3.0 + 0.05)D) 57.2 tanh
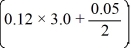
E)
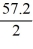 tanh
tanh 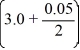
57.2 tanh 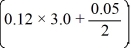
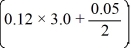
3
The velocity (measured in meters per second) of an air-dropped container of food and supplies affixed to a parachute is described by the function v(t) = 65.6 tanh(0.19t), t 3.0, where t is measured in seconds. You are interested in approximating the vertical distance s(t) traveled by the package by time t = 3.10 seconds.Using a step size of h = 0.10 seconds, compute the vertical distance traveled in the first 3.10 seconds.
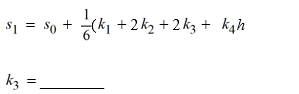
A) 65.6 tanh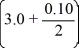
B) 65.6 tanh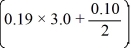
C)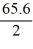 tanh
tanh 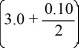
D)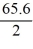 tanh(3.0 + 0.10)
tanh(3.0 + 0.10)
E) 65.6 tanh(0.19 × (3.0 + 0.10))
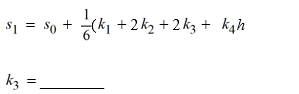
A) 65.6 tanh
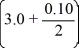
B) 65.6 tanh
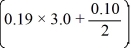
C)
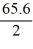 tanh
tanh 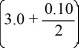
D)
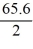 tanh(3.0 + 0.10)
tanh(3.0 + 0.10)E) 65.6 tanh(0.19 × (3.0 + 0.10))
65.6 tanh 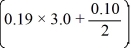
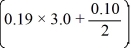
4
The velocity (measured in meters per second) of an air-dropped container of food and supplies affixed to a parachute is described by the function v(t) = 56 tanh(0.23t), t 3.2, where t is measured in seconds. You are interested in approximating the vertical distance s(t) traveled by the package by time t = 3.45 seconds.Using a step size of h = 0.25 seconds, compute the vertical distance traveled in the first 3.45 seconds.
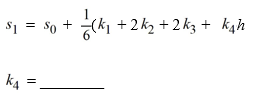
A) 56 tanh(0.23 × (3.2 + 0.25))
B) tanh(0.23 × (3.2 + 0.25))
C) 56 tanh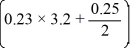
D)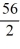 tanh(0.23 × (3.2+ 0.25))
tanh(0.23 × (3.2+ 0.25))
E)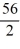 tanh
tanh 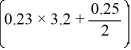
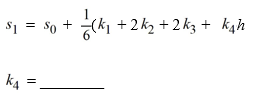
A) 56 tanh(0.23 × (3.2 + 0.25))
B) tanh(0.23 × (3.2 + 0.25))
C) 56 tanh
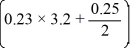
D)
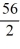 tanh(0.23 × (3.2+ 0.25))
tanh(0.23 × (3.2+ 0.25))E)
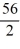 tanh
tanh 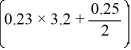

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
5
Consider the following initial value problem
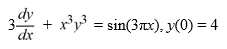
How would you need to rewrite this problem in order to apply the Runge-Kutta 4th order method to approximate the solution of this problem at a value of x?
A)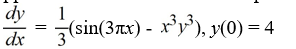
B)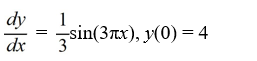
C)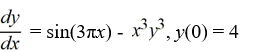
D)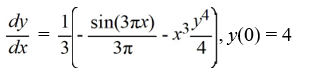
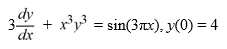
How would you need to rewrite this problem in order to apply the Runge-Kutta 4th order method to approximate the solution of this problem at a value of x?
A)
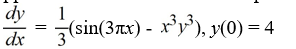
B)
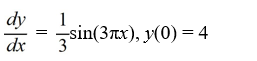
C)
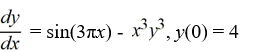
D)
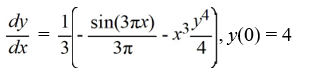

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
6
Consider the following initial value problem
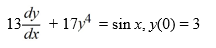
How would you need to rewrite this problem in order to apply Euler's method to approximate the solution of this problem at a value of x?
A)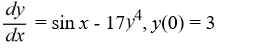
B)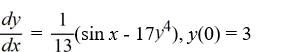
C)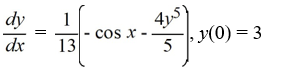
D)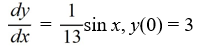
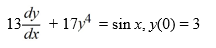
How would you need to rewrite this problem in order to apply Euler's method to approximate the solution of this problem at a value of x?
A)
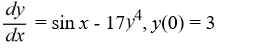
B)
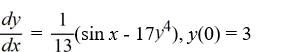
C)
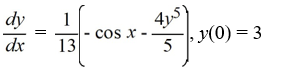
D)
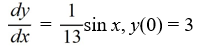

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
7
Consider the following initial value problem
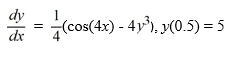
The following question pertains to the various computational steps and identifications involved in applying Runge-Kutta's 4th order method to evaluate y(0.7).
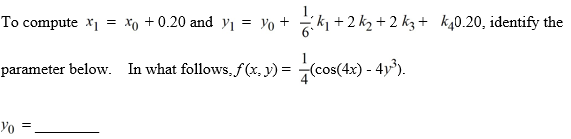
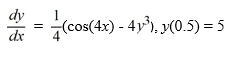
The following question pertains to the various computational steps and identifications involved in applying Runge-Kutta's 4th order method to evaluate y(0.7).
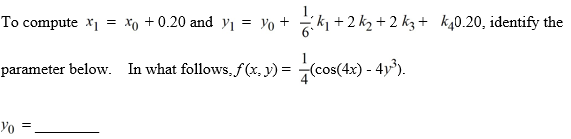

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
8
Consider the following initial value problem
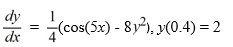
The following question pertains to the various computational steps and identifications involved in applying Runge-Kutta's 4th order method to evaluate y(0.55).
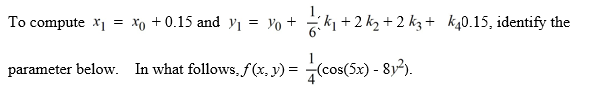
x0 = ________
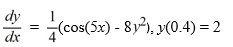
The following question pertains to the various computational steps and identifications involved in applying Runge-Kutta's 4th order method to evaluate y(0.55).
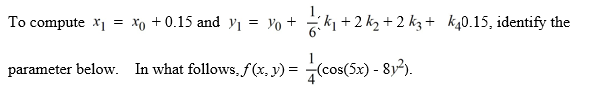
x0 = ________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
9
Consider the following initial value problem

A)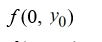
B)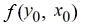
C)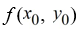
D)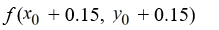

A)
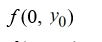
B)
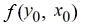
C)
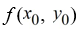
D)
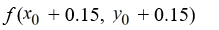

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
10
Consider the following initial value problem
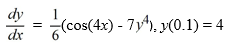
The following question pertains to the various computational steps and identifications involved in applying Runge-Kutta's 4th order method to evaluate y(0.15).
To compute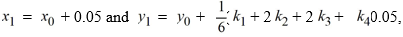
identify the parameter below. In what follows,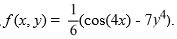
K2 = ________
A)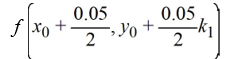
B)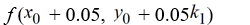
C)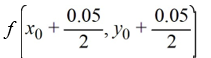
D)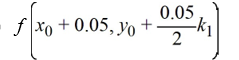
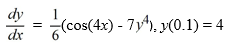
The following question pertains to the various computational steps and identifications involved in applying Runge-Kutta's 4th order method to evaluate y(0.15).
To compute
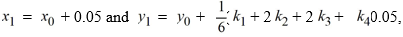
identify the parameter below. In what follows,
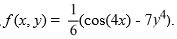
K2 = ________
A)
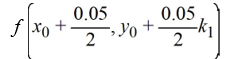
B)
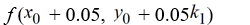
C)
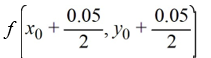
D)
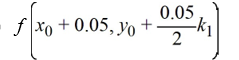

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
11
Consider the following initial value problem
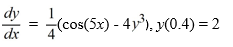
The following question pertains to the various computational steps and identifications involved in applying Runge-Kutta's 4th order method to evaluate y(0.6).
To compute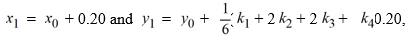
identify the parameter below. In what follows,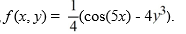
K3 = ________
A)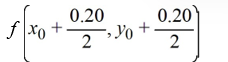
B)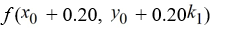
C)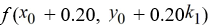
D)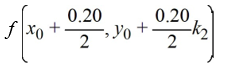
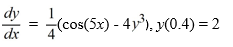
The following question pertains to the various computational steps and identifications involved in applying Runge-Kutta's 4th order method to evaluate y(0.6).
To compute
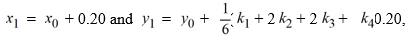
identify the parameter below. In what follows,
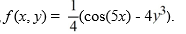
K3 = ________
A)
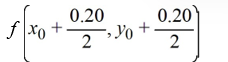
B)
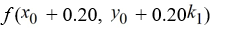
C)
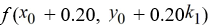
D)
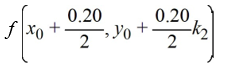

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
12
Consider the following initial value problem
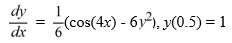
The following question pertains to the various computational steps and identifications involved in applying Runge-Kutta's 4th order method to evaluate y(0.7).
To compute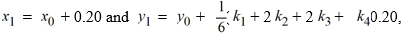
, identify the parameter below. In what follows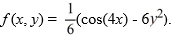
K4 = ________
A)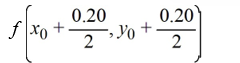
B)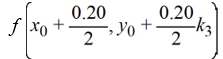
C)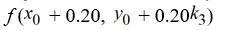
D)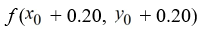
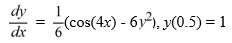
The following question pertains to the various computational steps and identifications involved in applying Runge-Kutta's 4th order method to evaluate y(0.7).
To compute
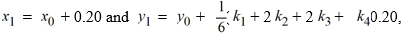
, identify the parameter below. In what follows
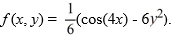
K4 = ________
A)
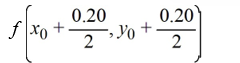
B)
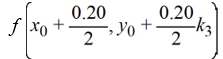
C)
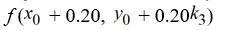
D)
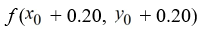

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
13
Given the initial value problem 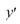 = 9y + 6t, y(0) = 5, how many steps n are needed for the Euler method to find an approximation for y(1.77) using a step size of h = 0.03?
= 9y + 6t, y(0) = 5, how many steps n are needed for the Euler method to find an approximation for y(1.77) using a step size of h = 0.03?
n ________
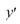 = 9y + 6t, y(0) = 5, how many steps n are needed for the Euler method to find an approximation for y(1.77) using a step size of h = 0.03?
= 9y + 6t, y(0) = 5, how many steps n are needed for the Euler method to find an approximation for y(1.77) using a step size of h = 0.03?n ________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
14
Given the initial value problem 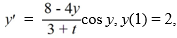 how many steps n are needed for the Euler method to find an approximation for y(4.6) using a step size of h = 0.06?
how many steps n are needed for the Euler method to find an approximation for y(4.6) using a step size of h = 0.06?
n = ________
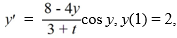 how many steps n are needed for the Euler method to find an approximation for y(4.6) using a step size of h = 0.06?
how many steps n are needed for the Euler method to find an approximation for y(4.6) using a step size of h = 0.06?n = ________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
15
Given the initial value problem 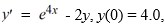 how many steps n are needed for the RK method to find an approximation for y(1.8) using a step size of h = 0.010?
how many steps n are needed for the RK method to find an approximation for y(1.8) using a step size of h = 0.010?
N = ________
A) n = 100
B) n = 180
C) n = 90
D) n = 360
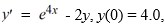 how many steps n are needed for the RK method to find an approximation for y(1.8) using a step size of h = 0.010?
how many steps n are needed for the RK method to find an approximation for y(1.8) using a step size of h = 0.010?N = ________
A) n = 100
B) n = 180
C) n = 90
D) n = 360

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
16
Consider the initial value problem 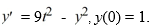 This question relates to using
This question relates to using
The Euler method to approximate the solution of this problem at t = 0.4 using a step size of h =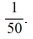
Which of the following identifications are correct when setting up Euler's method Select all that apply.
A)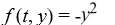
B)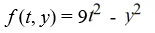
C)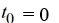
D)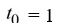
E)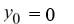
F)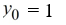
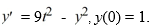 This question relates to using
This question relates to usingThe Euler method to approximate the solution of this problem at t = 0.4 using a step size of h =
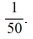
Which of the following identifications are correct when setting up Euler's method Select all that apply.
A)
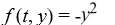
B)
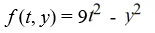
C)
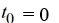
D)
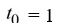
E)
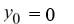
F)
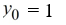

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
17
Consider the initial value problem 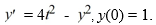 This question relates to using the Euler method to approximate the solution of this problem at t = 0.5 using a step size of h =
This question relates to using the Euler method to approximate the solution of this problem at t = 0.5 using a step size of h = 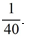 What are the correct values of
What are the correct values of 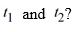
A)
B)
C)
D)
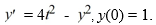 This question relates to using the Euler method to approximate the solution of this problem at t = 0.5 using a step size of h =
This question relates to using the Euler method to approximate the solution of this problem at t = 0.5 using a step size of h = 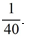 What are the correct values of
What are the correct values of 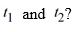
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
18
Consider the initial value problem 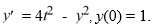 This question relates to using the Euler method to approximate the solution of this problem at t = 0.2 using a step size of h =
This question relates to using the Euler method to approximate the solution of this problem at t = 0.2 using a step size of h = 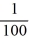
Y1 = ________
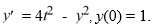 This question relates to using the Euler method to approximate the solution of this problem at t = 0.2 using a step size of h =
This question relates to using the Euler method to approximate the solution of this problem at t = 0.2 using a step size of h = 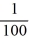
Y1 = ________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
19
Consider the initial value problem 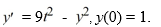 This question relates to using the Euler method to approximate the solution of this problem at t = 0.1 using a step size of h =
This question relates to using the Euler method to approximate the solution of this problem at t = 0.1 using a step size of h = 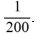 Which of the following equals
Which of the following equals 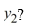
A)
B)
C)
D)
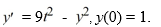 This question relates to using the Euler method to approximate the solution of this problem at t = 0.1 using a step size of h =
This question relates to using the Euler method to approximate the solution of this problem at t = 0.1 using a step size of h = 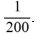 Which of the following equals
Which of the following equals 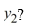
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
20
Consider the initial value problem 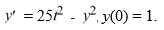 This question relates to using the backward Euler method to approximate the solution at t = 0.2, namely = y(0.2), using a step size of h = 0.02.
This question relates to using the backward Euler method to approximate the solution at t = 0.2, namely = y(0.2), using a step size of h = 0.02.
Which of these identifications are correct when setting up the backward Euler method? Select all that apply.
A)
B)
C)
D)
E)
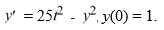 This question relates to using the backward Euler method to approximate the solution at t = 0.2, namely = y(0.2), using a step size of h = 0.02.
This question relates to using the backward Euler method to approximate the solution at t = 0.2, namely = y(0.2), using a step size of h = 0.02.Which of these identifications are correct when setting up the backward Euler method? Select all that apply.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
21
Consider the initial value problem 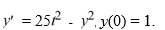 This question relates to using the backward Euler method to approximate the solution at t = 0.4, namely = y(0.4), using a step size of h = 0.02.
This question relates to using the backward Euler method to approximate the solution at t = 0.4, namely = y(0.4), using a step size of h = 0.02.
Which of these equations is the result of applying the backward Euler method to solve for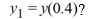
A)
B)
C)
D)
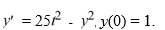 This question relates to using the backward Euler method to approximate the solution at t = 0.4, namely = y(0.4), using a step size of h = 0.02.
This question relates to using the backward Euler method to approximate the solution at t = 0.4, namely = y(0.4), using a step size of h = 0.02.Which of these equations is the result of applying the backward Euler method to solve for
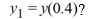
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
22
Consider the initial value problem 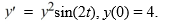 Use the Runge-Kutta method to approximate the solution at
Use the Runge-Kutta method to approximate the solution at 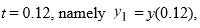 using a step size of h = 0.12.
using a step size of h = 0.12.
(a) Find the following constants needed for the Runge-Kutta method.
(i) K 1= ________
(ii) K 2= ________
(iii) K 3= ________
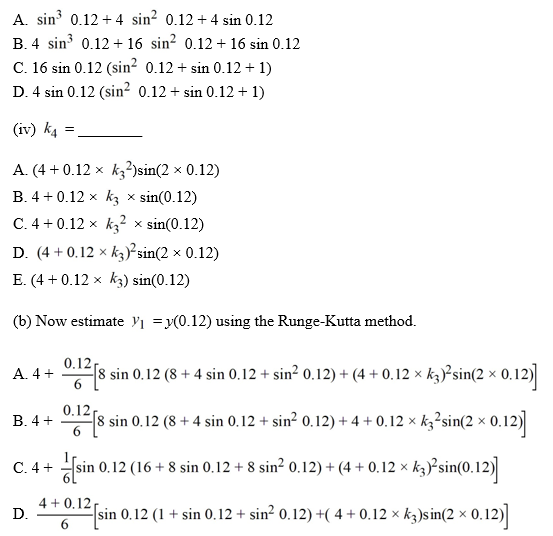
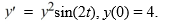 Use the Runge-Kutta method to approximate the solution at
Use the Runge-Kutta method to approximate the solution at 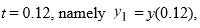 using a step size of h = 0.12.
using a step size of h = 0.12.(a) Find the following constants needed for the Runge-Kutta method.
(i) K 1= ________
(ii) K 2= ________
(iii) K 3= ________
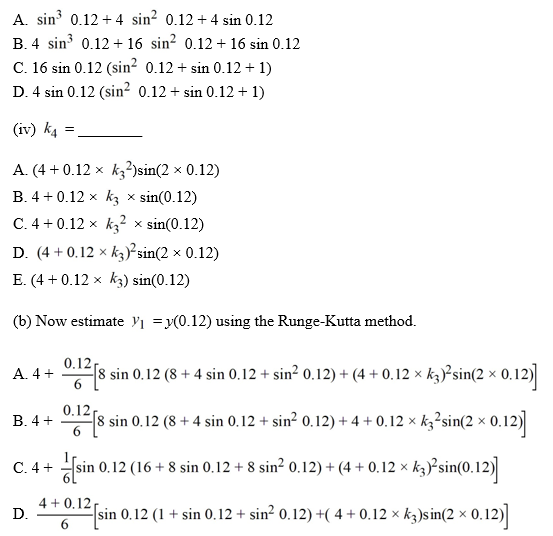

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
23
Consider the initial value problem 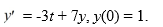 This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
Which of the following is the correct formula for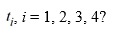
A)
B)
C)
D)
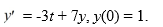 This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.Which of the following is the correct formula for
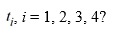
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
24
Consider the initial value problem 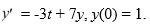 This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
For this problem, you will need these values to carry out the computations:
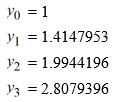
Which of the following is the correct formula for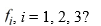
A)
B)
C)
D)
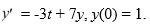 This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.For this problem, you will need these values to carry out the computations:
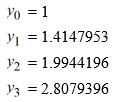
Which of the following is the correct formula for
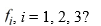
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
25
Consider the initial value problem ![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following is the predicted value for </strong> A) y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right] B) y_{3}+\frac{0.05}{24}\left[59\left(-3 \times 0.15+7 y_{3}\right)-55\left(-3 \times 0.10+7 y_{2}\right)-37\left(-3 \times 0.05+7 y_{1}\right)+9 \times 5\right] C) y_{3}+\frac{1}{24}\left[59\left(-3 \times 0.15+7 y_{3}\right)-55\left(-3 \times 0.10+7 y_{2}\right)-37\left(-3 \times 0.05+7 y_{1}\right)+9 \times 5\right] D) y_{3}+\frac{1}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]](https://storage.examlex.com/TBW1042/11eeb833_703c_0b25_9020_3dfd7ec29043_TBW1042_11.jpg) This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
For this problem, you will need these values to carry out the computations:
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following is the predicted value for </strong> A) y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right] B) y_{3}+\frac{0.05}{24}\left[59\left(-3 \times 0.15+7 y_{3}\right)-55\left(-3 \times 0.10+7 y_{2}\right)-37\left(-3 \times 0.05+7 y_{1}\right)+9 \times 5\right] C) y_{3}+\frac{1}{24}\left[59\left(-3 \times 0.15+7 y_{3}\right)-55\left(-3 \times 0.10+7 y_{2}\right)-37\left(-3 \times 0.05+7 y_{1}\right)+9 \times 5\right] D) y_{3}+\frac{1}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]](https://storage.examlex.com/TBW1042/11eeb833_703c_0b26_9020_11a22a46da11_TBW1042_11.jpg)
Which of the following is the predicted value for![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following is the predicted value for </strong> A) y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right] B) y_{3}+\frac{0.05}{24}\left[59\left(-3 \times 0.15+7 y_{3}\right)-55\left(-3 \times 0.10+7 y_{2}\right)-37\left(-3 \times 0.05+7 y_{1}\right)+9 \times 5\right] C) y_{3}+\frac{1}{24}\left[59\left(-3 \times 0.15+7 y_{3}\right)-55\left(-3 \times 0.10+7 y_{2}\right)-37\left(-3 \times 0.05+7 y_{1}\right)+9 \times 5\right] D) y_{3}+\frac{1}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]](https://storage.examlex.com/TBW1042/11eeb833_703c_0b27_9020_6385aa4eb0fd_TBW1042_11.jpg)
A)
B)
C)
D)
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following is the predicted value for </strong> A) y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right] B) y_{3}+\frac{0.05}{24}\left[59\left(-3 \times 0.15+7 y_{3}\right)-55\left(-3 \times 0.10+7 y_{2}\right)-37\left(-3 \times 0.05+7 y_{1}\right)+9 \times 5\right] C) y_{3}+\frac{1}{24}\left[59\left(-3 \times 0.15+7 y_{3}\right)-55\left(-3 \times 0.10+7 y_{2}\right)-37\left(-3 \times 0.05+7 y_{1}\right)+9 \times 5\right] D) y_{3}+\frac{1}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]](https://storage.examlex.com/TBW1042/11eeb833_703c_0b25_9020_3dfd7ec29043_TBW1042_11.jpg) This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.For this problem, you will need these values to carry out the computations:
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following is the predicted value for </strong> A) y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right] B) y_{3}+\frac{0.05}{24}\left[59\left(-3 \times 0.15+7 y_{3}\right)-55\left(-3 \times 0.10+7 y_{2}\right)-37\left(-3 \times 0.05+7 y_{1}\right)+9 \times 5\right] C) y_{3}+\frac{1}{24}\left[59\left(-3 \times 0.15+7 y_{3}\right)-55\left(-3 \times 0.10+7 y_{2}\right)-37\left(-3 \times 0.05+7 y_{1}\right)+9 \times 5\right] D) y_{3}+\frac{1}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]](https://storage.examlex.com/TBW1042/11eeb833_703c_0b26_9020_11a22a46da11_TBW1042_11.jpg)
Which of the following is the predicted value for
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following is the predicted value for </strong> A) y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right] B) y_{3}+\frac{0.05}{24}\left[59\left(-3 \times 0.15+7 y_{3}\right)-55\left(-3 \times 0.10+7 y_{2}\right)-37\left(-3 \times 0.05+7 y_{1}\right)+9 \times 5\right] C) y_{3}+\frac{1}{24}\left[59\left(-3 \times 0.15+7 y_{3}\right)-55\left(-3 \times 0.10+7 y_{2}\right)-37\left(-3 \times 0.05+7 y_{1}\right)+9 \times 5\right] D) y_{3}+\frac{1}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]](https://storage.examlex.com/TBW1042/11eeb833_703c_0b27_9020_6385aa4eb0fd_TBW1042_11.jpg)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
26
Consider the initial value problem ![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: To use the corrector formula, you need . Which of the following is the correct expression for ?</strong> A) 0.2 \times(-3)-7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) B) 7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) C) 0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) D) -7 \times\left[y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right]^{\prime}](https://storage.examlex.com/TBW1042/11eeb833_703c_0b29_9020_c9f8a5faaa07_TBW1042_11.jpg) This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
For this problem, you will need these values to carry out the computations:
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: To use the corrector formula, you need . Which of the following is the correct expression for ?</strong> A) 0.2 \times(-3)-7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) B) 7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) C) 0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) D) -7 \times\left[y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right]^{\prime}](https://storage.examlex.com/TBW1042/11eeb833_703c_0b2a_9020_85668c832878_TBW1042_11.jpg)
To use the corrector formula, you need![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: To use the corrector formula, you need . Which of the following is the correct expression for ?</strong> A) 0.2 \times(-3)-7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) B) 7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) C) 0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) D) -7 \times\left[y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right]^{\prime}](https://storage.examlex.com/TBW1042/11eeb833_703c_0b2b_9020_319b0011821e_TBW1042_11.jpg) . Which of the following is the correct expression for
. Which of the following is the correct expression for ![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: To use the corrector formula, you need . Which of the following is the correct expression for ?</strong> A) 0.2 \times(-3)-7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) B) 7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) C) 0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) D) -7 \times\left[y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right]^{\prime}](https://storage.examlex.com/TBW1042/11eeb833_703c_0b2c_9020_5d57575dd7dc_TBW1042_11.jpg) ?
?
A)
B)
C)
D)
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: To use the corrector formula, you need . Which of the following is the correct expression for ?</strong> A) 0.2 \times(-3)-7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) B) 7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) C) 0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) D) -7 \times\left[y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right]^{\prime}](https://storage.examlex.com/TBW1042/11eeb833_703c_0b29_9020_c9f8a5faaa07_TBW1042_11.jpg) This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.For this problem, you will need these values to carry out the computations:
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: To use the corrector formula, you need . Which of the following is the correct expression for ?</strong> A) 0.2 \times(-3)-7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) B) 7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) C) 0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) D) -7 \times\left[y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right]^{\prime}](https://storage.examlex.com/TBW1042/11eeb833_703c_0b2a_9020_85668c832878_TBW1042_11.jpg)
To use the corrector formula, you need
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: To use the corrector formula, you need . Which of the following is the correct expression for ?</strong> A) 0.2 \times(-3)-7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) B) 7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) C) 0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) D) -7 \times\left[y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right]^{\prime}](https://storage.examlex.com/TBW1042/11eeb833_703c_0b2b_9020_319b0011821e_TBW1042_11.jpg) . Which of the following is the correct expression for
. Which of the following is the correct expression for ![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: To use the corrector formula, you need . Which of the following is the correct expression for ?</strong> A) 0.2 \times(-3)-7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) B) 7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) C) 0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right) D) -7 \times\left[y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right]^{\prime}](https://storage.examlex.com/TBW1042/11eeb833_703c_0b2c_9020_5d57575dd7dc_TBW1042_11.jpg) ?
?A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the initial value problem ![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following show a portion of the formula for the corrected value of </strong> A) y_{3}+\frac{9 \times 0.05}{24}\left[0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) B) y_{3}-\frac{9 \times 0.05}{24}\left(0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) C) y_{3}+\frac{37 \times 0.05}{24}\left(7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) D) y_{3}-\frac{37 \times 0.05}{24}\left(7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right)](https://storage.examlex.com/TBW1042/11eeb833_703c_323e_9020_13a4ca37b6ab_TBW1042_11.jpg) This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
For this problem, you will need these values to carry out the computations:
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following show a portion of the formula for the corrected value of </strong> A) y_{3}+\frac{9 \times 0.05}{24}\left[0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) B) y_{3}-\frac{9 \times 0.05}{24}\left(0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) C) y_{3}+\frac{37 \times 0.05}{24}\left(7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) D) y_{3}-\frac{37 \times 0.05}{24}\left(7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right)](https://storage.examlex.com/TBW1042/11eeb833_703c_323f_9020_09cddb2cd944_TBW1042_11.jpg)
Which of the following show a portion of the formula for the corrected value of![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following show a portion of the formula for the corrected value of </strong> A) y_{3}+\frac{9 \times 0.05}{24}\left[0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) B) y_{3}-\frac{9 \times 0.05}{24}\left(0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) C) y_{3}+\frac{37 \times 0.05}{24}\left(7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) D) y_{3}-\frac{37 \times 0.05}{24}\left(7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right)](https://storage.examlex.com/TBW1042/11eeb833_703c_3240_9020_cb6077dbf68d_TBW1042_11.jpg)
A)
B)
C)
D)
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following show a portion of the formula for the corrected value of </strong> A) y_{3}+\frac{9 \times 0.05}{24}\left[0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) B) y_{3}-\frac{9 \times 0.05}{24}\left(0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) C) y_{3}+\frac{37 \times 0.05}{24}\left(7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) D) y_{3}-\frac{37 \times 0.05}{24}\left(7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right)](https://storage.examlex.com/TBW1042/11eeb833_703c_323e_9020_13a4ca37b6ab_TBW1042_11.jpg) This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.For this problem, you will need these values to carry out the computations:
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following show a portion of the formula for the corrected value of </strong> A) y_{3}+\frac{9 \times 0.05}{24}\left[0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) B) y_{3}-\frac{9 \times 0.05}{24}\left(0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) C) y_{3}+\frac{37 \times 0.05}{24}\left(7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) D) y_{3}-\frac{37 \times 0.05}{24}\left(7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right)](https://storage.examlex.com/TBW1042/11eeb833_703c_323f_9020_09cddb2cd944_TBW1042_11.jpg)
Which of the following show a portion of the formula for the corrected value of
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following show a portion of the formula for the corrected value of </strong> A) y_{3}+\frac{9 \times 0.05}{24}\left[0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) B) y_{3}-\frac{9 \times 0.05}{24}\left(0.2 \times(-3)+7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) C) y_{3}+\frac{37 \times 0.05}{24}\left(7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right) D) y_{3}-\frac{37 \times 0.05}{24}\left(7 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(-3 \times 0.15+7 y_{3}\right)-59\left(-3 \times 0.10+7 y_{2}\right)+37\left(-3 \times 0.05+7 y_{1}\right)-9 \times 5\right]\right)\right)](https://storage.examlex.com/TBW1042/11eeb833_703c_3240_9020_cb6077dbf68d_TBW1042_11.jpg)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
28
Consider the initial value problem 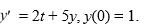 This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
Which of the following is the correct formula for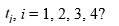
A)
B)
C)
D)
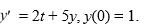 This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.Which of the following is the correct formula for
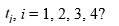
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
29
Consider the initial value problem 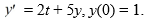 This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
For this problem, you will need these values to carry out the computations:
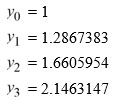
Which of the following is the correct formula for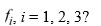
A)
B)
C)
D)
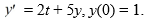 This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.For this problem, you will need these values to carry out the computations:
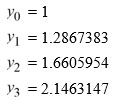
Which of the following is the correct formula for
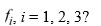
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
30
Consider the initial value problem ![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following is the predicted value for </strong> A) y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right] B) y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-37\left(2 \times 0.10+5 y_{2}\right)+9\left(2 \times 0.05+5 y_{1}\right)-1 \times 5\right] C) y_{3}+\frac{1}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-37\left(2 \times 0.10+5 y_{2}\right)+9\left(2 \times 0.05+5 y_{1}\right)-1 \times 5\right] D) y_{3}+\frac{1}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]](https://storage.examlex.com/TBW1042/11eeb833_703c_3249_9020_9bd561ff9a25_TBW1042_11.jpg) This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
For this problem, you will need these values to carry out the computations:
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following is the predicted value for </strong> A) y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right] B) y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-37\left(2 \times 0.10+5 y_{2}\right)+9\left(2 \times 0.05+5 y_{1}\right)-1 \times 5\right] C) y_{3}+\frac{1}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-37\left(2 \times 0.10+5 y_{2}\right)+9\left(2 \times 0.05+5 y_{1}\right)-1 \times 5\right] D) y_{3}+\frac{1}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]](https://storage.examlex.com/TBW1042/11eeb833_703c_324a_9020_259c3d72b679_TBW1042_11.jpg)
Which of the following is the predicted value for![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following is the predicted value for </strong> A) y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right] B) y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-37\left(2 \times 0.10+5 y_{2}\right)+9\left(2 \times 0.05+5 y_{1}\right)-1 \times 5\right] C) y_{3}+\frac{1}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-37\left(2 \times 0.10+5 y_{2}\right)+9\left(2 \times 0.05+5 y_{1}\right)-1 \times 5\right] D) y_{3}+\frac{1}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]](https://storage.examlex.com/TBW1042/11eeb833_703c_324b_9020_b1d6ec2c336f_TBW1042_11.jpg)
A)
B)
C)
D)
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following is the predicted value for </strong> A) y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right] B) y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-37\left(2 \times 0.10+5 y_{2}\right)+9\left(2 \times 0.05+5 y_{1}\right)-1 \times 5\right] C) y_{3}+\frac{1}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-37\left(2 \times 0.10+5 y_{2}\right)+9\left(2 \times 0.05+5 y_{1}\right)-1 \times 5\right] D) y_{3}+\frac{1}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]](https://storage.examlex.com/TBW1042/11eeb833_703c_3249_9020_9bd561ff9a25_TBW1042_11.jpg) This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.For this problem, you will need these values to carry out the computations:
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following is the predicted value for </strong> A) y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right] B) y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-37\left(2 \times 0.10+5 y_{2}\right)+9\left(2 \times 0.05+5 y_{1}\right)-1 \times 5\right] C) y_{3}+\frac{1}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-37\left(2 \times 0.10+5 y_{2}\right)+9\left(2 \times 0.05+5 y_{1}\right)-1 \times 5\right] D) y_{3}+\frac{1}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]](https://storage.examlex.com/TBW1042/11eeb833_703c_324a_9020_259c3d72b679_TBW1042_11.jpg)
Which of the following is the predicted value for
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following is the predicted value for </strong> A) y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right] B) y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-37\left(2 \times 0.10+5 y_{2}\right)+9\left(2 \times 0.05+5 y_{1}\right)-1 \times 5\right] C) y_{3}+\frac{1}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-37\left(2 \times 0.10+5 y_{2}\right)+9\left(2 \times 0.05+5 y_{1}\right)-1 \times 5\right] D) y_{3}+\frac{1}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]](https://storage.examlex.com/TBW1042/11eeb833_703c_324b_9020_b1d6ec2c336f_TBW1042_11.jpg)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
31
Consider the initial value problem ![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: To use the corrector formula, you need f<sub>4</sub> . Which of the following is the correct expression for f<sub>4</sub></strong> A) 0.2 \times 2-5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right] B) 5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right) C) 0.2 \times 2+5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right] D) -5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right]](https://storage.examlex.com/TBW1042/11eeb833_703c_595d_9020_97e1d504bb0a_TBW1042_11.jpg) This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
For this problem, you will need these values to carry out the computations:
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: To use the corrector formula, you need f<sub>4</sub> . Which of the following is the correct expression for f<sub>4</sub></strong> A) 0.2 \times 2-5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right] B) 5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right) C) 0.2 \times 2+5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right] D) -5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right]](https://storage.examlex.com/TBW1042/11eeb833_703c_595e_9020_f57932bf59be_TBW1042_11.jpg)
To use the corrector formula, you need f4 . Which of the following is the correct expression for f4
A)
B)
C)
D)
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: To use the corrector formula, you need f<sub>4</sub> . Which of the following is the correct expression for f<sub>4</sub></strong> A) 0.2 \times 2-5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right] B) 5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right) C) 0.2 \times 2+5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right] D) -5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right]](https://storage.examlex.com/TBW1042/11eeb833_703c_595d_9020_97e1d504bb0a_TBW1042_11.jpg) This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.For this problem, you will need these values to carry out the computations:
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: To use the corrector formula, you need f<sub>4</sub> . Which of the following is the correct expression for f<sub>4</sub></strong> A) 0.2 \times 2-5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right] B) 5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right) C) 0.2 \times 2+5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right] D) -5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right]](https://storage.examlex.com/TBW1042/11eeb833_703c_595e_9020_f57932bf59be_TBW1042_11.jpg)
To use the corrector formula, you need f4 . Which of the following is the correct expression for f4
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
32
Consider the initial value problem ![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following show a portion of the formula for the corrected value of </strong> A) y_{3}+\frac{9 \times 0.05}{24}\left(0.2 \times 2+5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) B) y_{3}-\frac{9 \times 0.05}{24}\left(0.2 \times 2+5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) C) y_{3}+\frac{37 \times 0.05}{24}\left(5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) D) y_{3}-\frac{37 \times 0.05}{24}\left(5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 57\right]\right)\right.](https://storage.examlex.com/TBW1042/11eeb833_703c_5960_9020_53f94286b202_TBW1042_11.jpg) This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
For this problem, you will need these values to carry out the computations:
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following show a portion of the formula for the corrected value of </strong> A) y_{3}+\frac{9 \times 0.05}{24}\left(0.2 \times 2+5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) B) y_{3}-\frac{9 \times 0.05}{24}\left(0.2 \times 2+5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) C) y_{3}+\frac{37 \times 0.05}{24}\left(5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) D) y_{3}-\frac{37 \times 0.05}{24}\left(5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 57\right]\right)\right.](https://storage.examlex.com/TBW1042/11eeb833_703c_5961_9020_3dd1cd44e1de_TBW1042_11.jpg)
Which of the following show a portion of the formula for the corrected value of![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following show a portion of the formula for the corrected value of </strong> A) y_{3}+\frac{9 \times 0.05}{24}\left(0.2 \times 2+5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) B) y_{3}-\frac{9 \times 0.05}{24}\left(0.2 \times 2+5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) C) y_{3}+\frac{37 \times 0.05}{24}\left(5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) D) y_{3}-\frac{37 \times 0.05}{24}\left(5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 57\right]\right)\right.](https://storage.examlex.com/TBW1042/11eeb833_703c_5962_9020_adc385b14f0c_TBW1042_11.jpg)
A)
B)
C)
D)
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following show a portion of the formula for the corrected value of </strong> A) y_{3}+\frac{9 \times 0.05}{24}\left(0.2 \times 2+5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) B) y_{3}-\frac{9 \times 0.05}{24}\left(0.2 \times 2+5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) C) y_{3}+\frac{37 \times 0.05}{24}\left(5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) D) y_{3}-\frac{37 \times 0.05}{24}\left(5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 57\right]\right)\right.](https://storage.examlex.com/TBW1042/11eeb833_703c_5960_9020_53f94286b202_TBW1042_11.jpg) This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.
This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05.For this problem, you will need these values to carry out the computations:
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following show a portion of the formula for the corrected value of </strong> A) y_{3}+\frac{9 \times 0.05}{24}\left(0.2 \times 2+5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) B) y_{3}-\frac{9 \times 0.05}{24}\left(0.2 \times 2+5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) C) y_{3}+\frac{37 \times 0.05}{24}\left(5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) D) y_{3}-\frac{37 \times 0.05}{24}\left(5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 57\right]\right)\right.](https://storage.examlex.com/TBW1042/11eeb833_703c_5961_9020_3dd1cd44e1de_TBW1042_11.jpg)
Which of the following show a portion of the formula for the corrected value of
![<strong>Consider the initial value problem This question is related to using the predictor-corrector method to estimate the solution y(0.2) using a step size of h = 0.05. For this problem, you will need these values to carry out the computations: Which of the following show a portion of the formula for the corrected value of </strong> A) y_{3}+\frac{9 \times 0.05}{24}\left(0.2 \times 2+5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) B) y_{3}-\frac{9 \times 0.05}{24}\left(0.2 \times 2+5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) C) y_{3}+\frac{37 \times 0.05}{24}\left(5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 5\right]\right)\right) D) y_{3}-\frac{37 \times 0.05}{24}\left(5 \times\left(y_{3}+\frac{0.05}{24}\left[55\left(2 \times 0.15+5 y_{3}\right)-59\left(2 \times 0.10+5 y_{2}\right)+37\left(2 \times 0.05+5 y_{1}\right)-9 \times 57\right]\right)\right.](https://storage.examlex.com/TBW1042/11eeb833_703c_5962_9020_adc385b14f0c_TBW1042_11.jpg)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
33
Consider the initial value problem 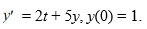 This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of .
This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of .
Which of these is the correct formula for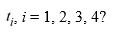
A)
B)
C)
D)
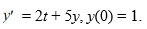 This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of .
This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of .Which of these is the correct formula for
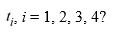
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
34
Consider the initial value problem 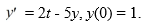 This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of h =0.05 .
This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of h =0.05 .
For the following problem, you will need these values to carry out the computation:

Which of the following is the value of
A)
B)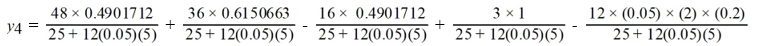
C)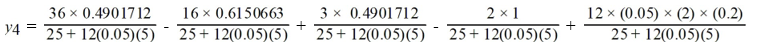
D)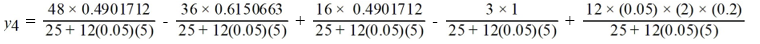
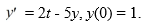 This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of h =0.05 .
This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of h =0.05 .For the following problem, you will need these values to carry out the computation:

Which of the following is the value of
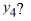
A)

B)
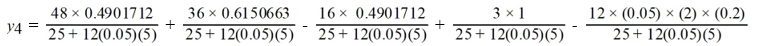
C)
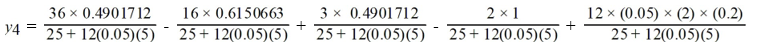
D)
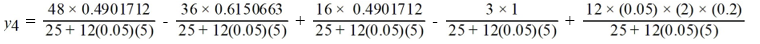

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
35
Consider the initial value problem 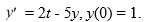 This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of h =0.05 .
This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of h =0.05 .
For the following problem, you will need these values to carry out the computation:

Which of the following expressions represents the error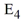 incurred in using this method to estimate y(0.2)?
incurred in using this method to estimate y(0.2)?
A)
B)
C)
D)
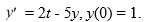 This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of h =0.05 .
This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of h =0.05 .For the following problem, you will need these values to carry out the computation:

Which of the following expressions represents the error
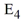 incurred in using this method to estimate y(0.2)?
incurred in using this method to estimate y(0.2)?A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
36
Consider the initial value problem 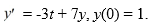 This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of h= 0.05
This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of h= 0.05
Which of these is the correct formula for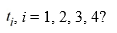
A)
B)
C)
D)
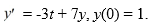 This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of h= 0.05
This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of h= 0.05Which of these is the correct formula for
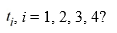
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
37
Consider the initial value problem 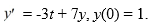 This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of .
This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of .
For the following problem, you will need these values to carry out the computation:
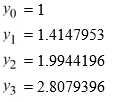
Which of the following is the value of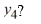
A)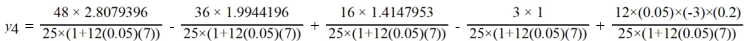
B)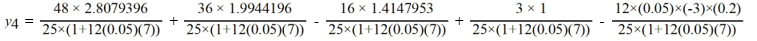
C)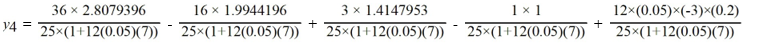
D)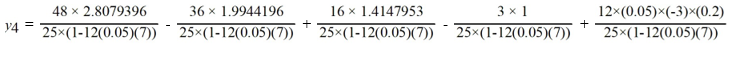
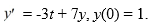 This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of .
This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of .For the following problem, you will need these values to carry out the computation:
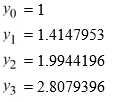
Which of the following is the value of
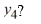
A)
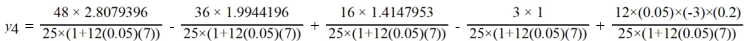
B)
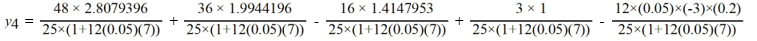
C)
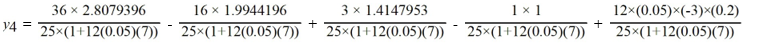
D)
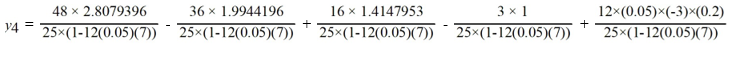

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
38
Consider the initial value problem 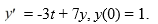 This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of h = 0.05 .
This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of h = 0.05 .
For the following problem, you will need these values to carry out the computation:
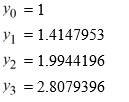
Which of the following expressions represents the error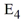 incurred in using this method to estimate y(0.2)?
incurred in using this method to estimate y(0.2)?
A)
B)
C)
D)
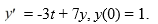 This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of h = 0.05 .
This question is related to using the fourth-order backward differentiation formula to estimate the solution y(0.2) using a step size of h = 0.05 .For the following problem, you will need these values to carry out the computation:
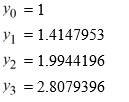
Which of the following expressions represents the error
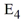 incurred in using this method to estimate y(0.2)?
incurred in using this method to estimate y(0.2)?A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
39
Consider the system of initial value problems given by
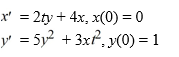
This problem can be expressed using matrix notation as
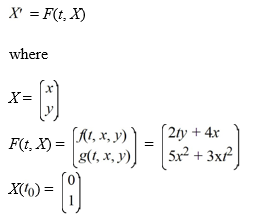
When using the Euler method with h = 0.05, how many iterations n do you need in order to estimate the solution at t = 2 × 0.05?
n = _______
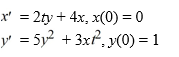
This problem can be expressed using matrix notation as
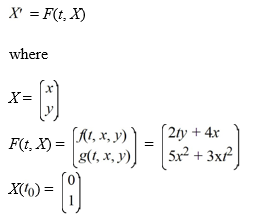
When using the Euler method with h = 0.05, how many iterations n do you need in order to estimate the solution at t = 2 × 0.05?
n = _______

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
40
Consider the system of initial value problems given by
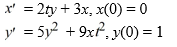
This problem can be expressed using matrix notation as
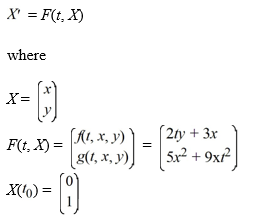
When using the Euler method with h = 0.1,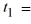 = ________
= ________
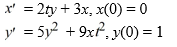
This problem can be expressed using matrix notation as
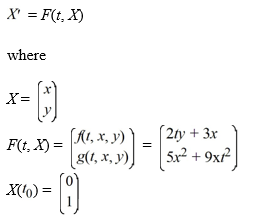
When using the Euler method with h = 0.1,
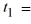 = ________
= ________
Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
41
Consider the system of initial value problems given by
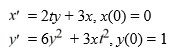
This problem can be expressed using matrix notation as
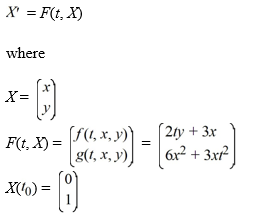
When using the Euler method with h = 0.05, what are the values of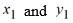 when using the Euler method?
when using the Euler method?
A)
B)
C)
D)
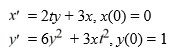
This problem can be expressed using matrix notation as
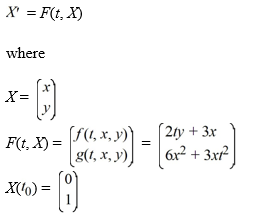
When using the Euler method with h = 0.05, what are the values of
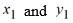 when using the Euler method?
when using the Euler method?A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
42
Consider the system of initial value problems given by
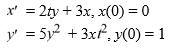
This problem can be expressed using matrix notation as
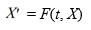
where
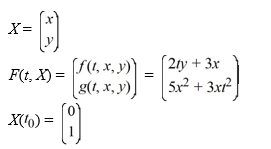
When using the Euler method with h = 0.1, t2 = ________
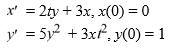
This problem can be expressed using matrix notation as
where
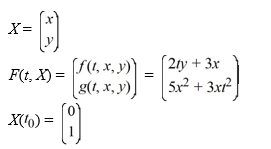
When using the Euler method with h = 0.1, t2 = ________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
43
Consider the system of initial value problems given by
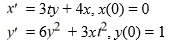
This problem can be expressed using matrix notation as
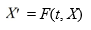
Where
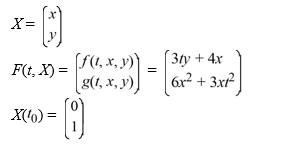
When using the Euler method with h = 0.05, what are the values of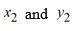
when using the Euler method?
A)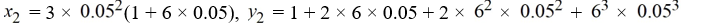
B)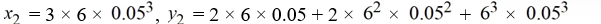
C)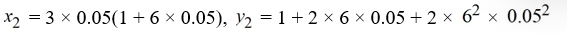
D)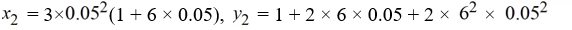
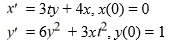
This problem can be expressed using matrix notation as
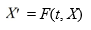
Where
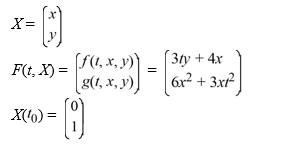
When using the Euler method with h = 0.05, what are the values of
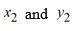
when using the Euler method?
A)
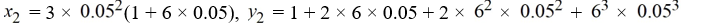
B)
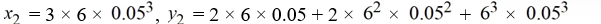
C)
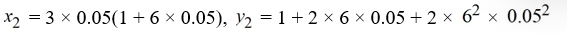
D)
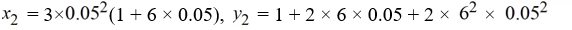

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
44
Consider the system of initial value problems given by
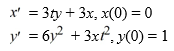
This problem can be expressed using matrix notation as
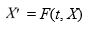
where
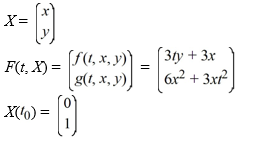
When using the improved Euler method with h = 0.05, how many iterations n do you need in order to estimate the solution yn at t = 0.10?
n = ________
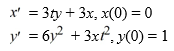
This problem can be expressed using matrix notation as
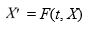
where
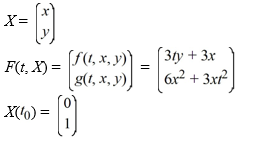
When using the improved Euler method with h = 0.05, how many iterations n do you need in order to estimate the solution yn at t = 0.10?
n = ________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
45
Consider the system of initial value problems given by
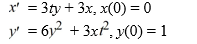
This problem can be expressed using matrix notation as
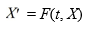
where
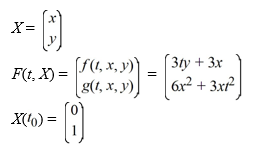
When using the improved Euler method with h = 0.05, ________
________
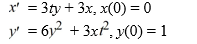
This problem can be expressed using matrix notation as
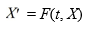
where
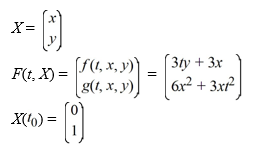
When using the improved Euler method with h = 0.05,
 ________
________
Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
46
Consider the system of initial value problems given by
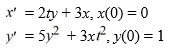
This problem can be expressed using matrix notation as
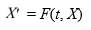
Where
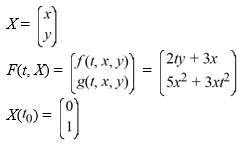
What are the values of when using the improved Euler method with h = 0.05?
when using the improved Euler method with h = 0.05?
A)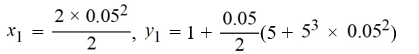
B)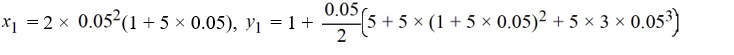
C)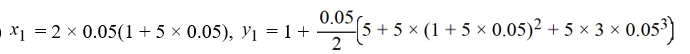
D)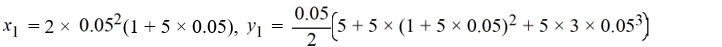
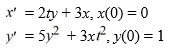
This problem can be expressed using matrix notation as
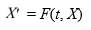
Where
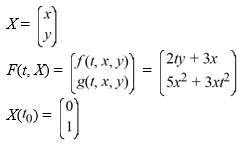
What are the values of
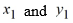 when using the improved Euler method with h = 0.05?
when using the improved Euler method with h = 0.05?A)
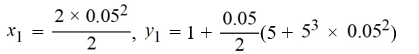
B)
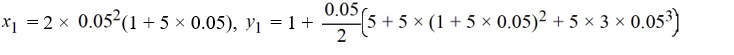
C)
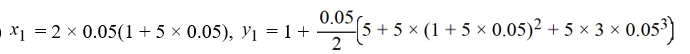
D)
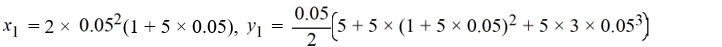

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
47
Consider the initial value problem
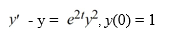
(Note: The exact solution is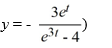
To apply the improved Euler method, which of the following expressions would you use for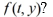
A)
B)
C)
D)
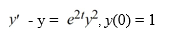
(Note: The exact solution is
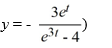
To apply the improved Euler method, which of the following expressions would you use for
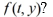
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
48
Consider the initial value problem
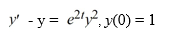
(Note: The exact solution is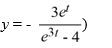
Using a step size of h = 0.25, compute the following approximations. Give your answers accurate to 6 decimal places.
(i) = ________
(ii) = ________
(iii) = ________
(iv) = ________
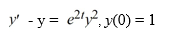
(Note: The exact solution is
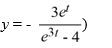
Using a step size of h = 0.25, compute the following approximations. Give your answers accurate to 6 decimal places.
(i) = ________
(ii) = ________
(iii) = ________
(iv) = ________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
49
Consider the initial value problem
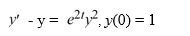
(Note: The exact solution is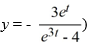
Which of the following expressions represents the error in the estimation for the improved Euler method?
E4 = ________
A)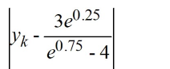
B)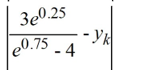
C)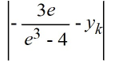
D)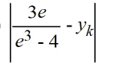
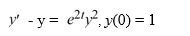
(Note: The exact solution is
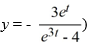
Which of the following expressions represents the error in the estimation for the improved Euler method?
E4 = ________
A)
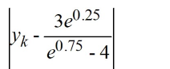
B)
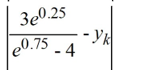
C)
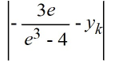
D)
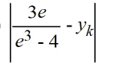

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
50
Consider the initial value problem
![<strong>Consider the initial value problem (Note: The exact solution is The size of the error e<sub>K</sub> is large because</strong> A) there is a vertical asymptote between [0, 1]. B) the step size is far from the initial time t<sub>0</sub> . C) the estimation y(1) is estimated far from the initial time t<sub>0</sub>. D) the function f (t) contains an exponential function e<sup>2t</sup>.](https://storage.examlex.com/TBW1042/11eeb833_703d_1cf0_9020_3334b9d5703d_TBW1042_11.jpg)
(Note: The exact solution is![<strong>Consider the initial value problem (Note: The exact solution is The size of the error e<sub>K</sub> is large because</strong> A) there is a vertical asymptote between [0, 1]. B) the step size is far from the initial time t<sub>0</sub> . C) the estimation y(1) is estimated far from the initial time t<sub>0</sub>. D) the function f (t) contains an exponential function e<sup>2t</sup>.](https://storage.examlex.com/TBW1042/11eeb833_703d_1cf1_9020_9b5737fb84da_TBW1042_11.jpg)
The size of the error eK is large because
A) there is a vertical asymptote between [0, 1].
B) the step size is far from the initial time t0 .
C) the estimation y(1) is estimated far from the initial time t0.
D) the function f (t) contains an exponential function e2t.
![<strong>Consider the initial value problem (Note: The exact solution is The size of the error e<sub>K</sub> is large because</strong> A) there is a vertical asymptote between [0, 1]. B) the step size is far from the initial time t<sub>0</sub> . C) the estimation y(1) is estimated far from the initial time t<sub>0</sub>. D) the function f (t) contains an exponential function e<sup>2t</sup>.](https://storage.examlex.com/TBW1042/11eeb833_703d_1cf0_9020_3334b9d5703d_TBW1042_11.jpg)
(Note: The exact solution is
![<strong>Consider the initial value problem (Note: The exact solution is The size of the error e<sub>K</sub> is large because</strong> A) there is a vertical asymptote between [0, 1]. B) the step size is far from the initial time t<sub>0</sub> . C) the estimation y(1) is estimated far from the initial time t<sub>0</sub>. D) the function f (t) contains an exponential function e<sup>2t</sup>.](https://storage.examlex.com/TBW1042/11eeb833_703d_1cf1_9020_9b5737fb84da_TBW1042_11.jpg)
The size of the error eK is large because
A) there is a vertical asymptote between [0, 1].
B) the step size is far from the initial time t0 .
C) the estimation y(1) is estimated far from the initial time t0.
D) the function f (t) contains an exponential function e2t.

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
51
Consider the initial value problem
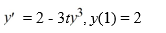
This question is related to using the Runge-Kutta method for approximating the solution y at t= 1.1 with a step size of h = 0.05.
How many approximations Yn are needed to estimate a solution at y(1.1) if h = 0.05?
n = ________
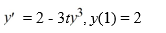
This question is related to using the Runge-Kutta method for approximating the solution y at t= 1.1 with a step size of h = 0.05.
How many approximations Yn are needed to estimate a solution at y(1.1) if h = 0.05?
n = ________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
52
Consider the initial value problem
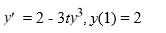
This question is related to using the Runge-Kutta method for approximating the solution y at t= 1.1 with a step size of h = 0.05.
To find Y1, first calculate the following in order to apply the Runge-Kutta method. Express your answers accurate to seven decimal places.
(i) K1 = ________
(ii) K2 = ________
(iii) K3 = ________
(iv) K4= ________
(v) So, using the Runge-Kutta method, Y1 = ________
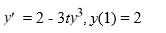
This question is related to using the Runge-Kutta method for approximating the solution y at t= 1.1 with a step size of h = 0.05.
To find Y1, first calculate the following in order to apply the Runge-Kutta method. Express your answers accurate to seven decimal places.
(i) K1 = ________
(ii) K2 = ________
(iii) K3 = ________
(iv) K4= ________
(v) So, using the Runge-Kutta method, Y1 = ________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
53
Consider the initial value problem
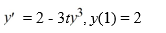
This question is related to using the Runge-Kutta method for approximating the solution y at with a step size of h = 0.05.
To find Y2 , first calculate the following in order to apply the Runge-Kutta method. Express your answers accurate to seven decimal places.
(i) K1 = ________
(ii) K2 = ________
(iii) K3 = ________
(iv) K4= ________
(v) So, using the Runge-Kutta method, Y2 = ________
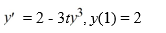
This question is related to using the Runge-Kutta method for approximating the solution y at with a step size of h = 0.05.
To find Y2 , first calculate the following in order to apply the Runge-Kutta method. Express your answers accurate to seven decimal places.
(i) K1 = ________
(ii) K2 = ________
(iii) K3 = ________
(iv) K4= ________
(v) So, using the Runge-Kutta method, Y2 = ________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
54
Consider the initial value problem
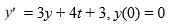
Use the backward Euler method with step size h = 0.01 to find the following approximation. Express your answer to 5 decimal places.
Y1________
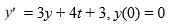
Use the backward Euler method with step size h = 0.01 to find the following approximation. Express your answer to 5 decimal places.
Y1________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
55
Consider the initial value problem
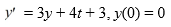
Use the backward Euler method with step size h = 0.01 to find the following approximation. Express your answer to 5 decimal places.
Y2________
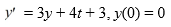
Use the backward Euler method with step size h = 0.01 to find the following approximation. Express your answer to 5 decimal places.
Y2________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
56
Consider the initial value problem
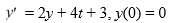
Use the backward Euler method with step size h = 0.01 to find the following approximation. Express your answer to 5 decimal places
Y3________
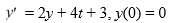
Use the backward Euler method with step size h = 0.01 to find the following approximation. Express your answer to 5 decimal places
Y3________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
57
Consider the following initial value problem on the interval [0, 1]
![Consider the following initial value problem on the interval [0, 1] Approximate the solution y(t) at t = 2.5 using the fourth-order backward differentiation formula with step size h = 0.05. Using the Runge-Kutta method you are provided with some initial Y<sub>n</sub> values to start the fourth-order backward differentiation formula. Y<sub>1</sub> = 2.157777 Y<sub>2</sub>= 2.3322791 Y<sub>3</sub> = 2.5253944 Use the fourth-order backward Euler differentiation formula to compute the following approximation. Express your answer accurate to 6 decimal places. Y<sub>4</sub> = ________](https://storage.examlex.com/TBW1042/11eeb833_703d_6b18_9020_bd1595a082b4_TBW1042_11.jpg)
Approximate the solution y(t) at t = 2.5 using the fourth-order backward differentiation formula with step size h = 0.05. Using the Runge-Kutta method you are provided with some initial Yn values to start the fourth-order backward differentiation formula.
Y1 = 2.157777
Y2= 2.3322791
Y3 = 2.5253944
Use the fourth-order backward Euler differentiation formula to compute the following approximation. Express your answer accurate to 6 decimal places.
Y4 = ________
![Consider the following initial value problem on the interval [0, 1] Approximate the solution y(t) at t = 2.5 using the fourth-order backward differentiation formula with step size h = 0.05. Using the Runge-Kutta method you are provided with some initial Y<sub>n</sub> values to start the fourth-order backward differentiation formula. Y<sub>1</sub> = 2.157777 Y<sub>2</sub>= 2.3322791 Y<sub>3</sub> = 2.5253944 Use the fourth-order backward Euler differentiation formula to compute the following approximation. Express your answer accurate to 6 decimal places. Y<sub>4</sub> = ________](https://storage.examlex.com/TBW1042/11eeb833_703d_6b18_9020_bd1595a082b4_TBW1042_11.jpg)
Approximate the solution y(t) at t = 2.5 using the fourth-order backward differentiation formula with step size h = 0.05. Using the Runge-Kutta method you are provided with some initial Yn values to start the fourth-order backward differentiation formula.
Y1 = 2.157777
Y2= 2.3322791
Y3 = 2.5253944
Use the fourth-order backward Euler differentiation formula to compute the following approximation. Express your answer accurate to 6 decimal places.
Y4 = ________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
58
Consider the following initial value problem on the interval [0, 1]
![Consider the following initial value problem on the interval [0, 1] Approximate the solution y(t) at t = 2.5 using the fourth-order backward differentiation formula with step size h = 0.05. Using the Runge-Kutta method you are provided with some initial Y<sub>n</sub> values to start the fourth-order backward differentiation formula. Y<sub>1</sub> = 2.157777 Y<sub>2</sub>= 2.3322791 Y<sub>3</sub> = 2.5253944 Use the fourth-order backward Euler differentiation formula to compute the following approximation. Express your answer accurate to 6 decimal places. Y<sub>5</sub> = ________](https://storage.examlex.com/TBW1042/11eeb833_703d_6b19_9020_e5b0e28017cd_TBW1042_11.jpg)
Approximate the solution y(t) at t = 2.5 using the fourth-order backward differentiation formula with step size h = 0.05. Using the Runge-Kutta method you are provided with some initial Yn values to start the fourth-order backward differentiation formula.
Y1 = 2.157777
Y2= 2.3322791
Y3 = 2.5253944
Use the fourth-order backward Euler differentiation formula to compute the following approximation. Express your answer accurate to 6 decimal places.
Y5 = ________
![Consider the following initial value problem on the interval [0, 1] Approximate the solution y(t) at t = 2.5 using the fourth-order backward differentiation formula with step size h = 0.05. Using the Runge-Kutta method you are provided with some initial Y<sub>n</sub> values to start the fourth-order backward differentiation formula. Y<sub>1</sub> = 2.157777 Y<sub>2</sub>= 2.3322791 Y<sub>3</sub> = 2.5253944 Use the fourth-order backward Euler differentiation formula to compute the following approximation. Express your answer accurate to 6 decimal places. Y<sub>5</sub> = ________](https://storage.examlex.com/TBW1042/11eeb833_703d_6b19_9020_e5b0e28017cd_TBW1042_11.jpg)
Approximate the solution y(t) at t = 2.5 using the fourth-order backward differentiation formula with step size h = 0.05. Using the Runge-Kutta method you are provided with some initial Yn values to start the fourth-order backward differentiation formula.
Y1 = 2.157777
Y2= 2.3322791
Y3 = 2.5253944
Use the fourth-order backward Euler differentiation formula to compute the following approximation. Express your answer accurate to 6 decimal places.
Y5 = ________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
59
Consider the initial value problem
![<strong> Consider the initial value problem The following table provides the estimation for the solution at different t values using the Euler and Improved Euler methods with a step size of 0.25. Based on the table above, which of the following is true regarding the given initial value problem?</strong> A) There is no numerical solution at y(0) = 1. B) A numerical solution can never be close to the exact solution. C) has a vertical asymptote for y(t) between [0.25, 1]. D) There is a solution which contains a horizontal asymptote. E) There is a solution which contains a vertical asymptote.](https://storage.examlex.com/TBW1042/11eeb833_703d_922a_9020_c7c5996e4490_TBW1042_00.jpg)
The following table provides the estimation for the solution at different t values using the Euler and Improved Euler methods with a step size of 0.25.
![<strong> Consider the initial value problem The following table provides the estimation for the solution at different t values using the Euler and Improved Euler methods with a step size of 0.25. Based on the table above, which of the following is true regarding the given initial value problem?</strong> A) There is no numerical solution at y(0) = 1. B) A numerical solution can never be close to the exact solution. C) has a vertical asymptote for y(t) between [0.25, 1]. D) There is a solution which contains a horizontal asymptote. E) There is a solution which contains a vertical asymptote.](https://storage.examlex.com/TBW1042/11eeb833_703d_922b_9020_e1ea8baf7b59_TBW1042_00.jpg)
Based on the table above, which of the following is true regarding the given initial value problem?
A) There is no numerical solution at y(0) = 1.
B) A numerical solution can never be close to the exact solution.
C) has a vertical asymptote for y(t) between [0.25, 1].
D) There is a solution which contains a horizontal asymptote.
E) There is a solution which contains a vertical asymptote.
![<strong> Consider the initial value problem The following table provides the estimation for the solution at different t values using the Euler and Improved Euler methods with a step size of 0.25. Based on the table above, which of the following is true regarding the given initial value problem?</strong> A) There is no numerical solution at y(0) = 1. B) A numerical solution can never be close to the exact solution. C) has a vertical asymptote for y(t) between [0.25, 1]. D) There is a solution which contains a horizontal asymptote. E) There is a solution which contains a vertical asymptote.](https://storage.examlex.com/TBW1042/11eeb833_703d_922a_9020_c7c5996e4490_TBW1042_00.jpg)
The following table provides the estimation for the solution at different t values using the Euler and Improved Euler methods with a step size of 0.25.
![<strong> Consider the initial value problem The following table provides the estimation for the solution at different t values using the Euler and Improved Euler methods with a step size of 0.25. Based on the table above, which of the following is true regarding the given initial value problem?</strong> A) There is no numerical solution at y(0) = 1. B) A numerical solution can never be close to the exact solution. C) has a vertical asymptote for y(t) between [0.25, 1]. D) There is a solution which contains a horizontal asymptote. E) There is a solution which contains a vertical asymptote.](https://storage.examlex.com/TBW1042/11eeb833_703d_922b_9020_e1ea8baf7b59_TBW1042_00.jpg)
Based on the table above, which of the following is true regarding the given initial value problem?
A) There is no numerical solution at y(0) = 1.
B) A numerical solution can never be close to the exact solution.
C) has a vertical asymptote for y(t) between [0.25, 1].
D) There is a solution which contains a horizontal asymptote.
E) There is a solution which contains a vertical asymptote.

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
60
For the following differential equation, use the fourth-order Adams-Moulton formula to estimate the solution at t = 0.4 using a step size of h = 0.1. To start the process, you are given some Yi values.

Calculate the following approximations. Express your answers accurate to 7 decimal places.
(i) f0 = ________
(ii) f1 = ________
(iii) f2 = ________
(iv) f3 = ________

Calculate the following approximations. Express your answers accurate to 7 decimal places.
(i) f0 = ________
(ii) f1 = ________
(iii) f2 = ________
(iv) f3 = ________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
61
For the following differential equation, use the fourth-order Adams-Moulton formula to estimate the solution at t = 0.4 using a step size of h = 0.1. To start the process, you are given some Yi values.

Using the fourth-order Adams-Moulton formula, approximate Y4 . Express your answer accurate to 7 decimal places.
Y4 = ________

Using the fourth-order Adams-Moulton formula, approximate Y4 . Express your answer accurate to 7 decimal places.
Y4 = ________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
62
For the following differential equation, use the fourth-order Adams-Moulton formula to estimate the solution at t = 0.4 using a step size of h = 0.1. To start the process, you are given some Yi values.

Calculate f4 = ________

Calculate f4 = ________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck
63
For the following differential equation, use the fourth-order Adams-Moulton formula to estimate the solution at t = 0.4 using a step size of h = 0.1. To start the process, you are given some Yi values.

Using the fourth-order Adams-Moulton formula, approximate Y5. Express your answer accurate to 7 decimal places.
Y5 = ________

Using the fourth-order Adams-Moulton formula, approximate Y5. Express your answer accurate to 7 decimal places.
Y5 = ________

Unlock Deck
Unlock for access to all 63 flashcards in this deck.
Unlock Deck
k this deck


