Deck 7: Systems of First-Order Linear Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/97
Play
Full screen (f)
Deck 7: Systems of First-Order Linear Equations
1
Into which of the following systems can this homogeneous second-order differential equation be transformed?
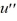 + 5
+ 5 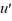 - 7 u = 0
- 7 u = 0
A)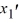 =
= 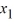 ,
, 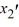 = 5
= 5 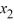 - 7
- 7 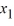
B)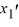 =
= 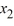 ,
, 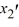 = 7
= 7 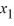 - 5
- 5 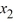
C)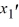 = -
= - 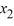 ,
, 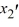 = 7
= 7 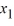 - 5
- 5 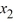
D)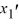 = -
= - 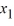 ,
, 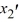 = 5
= 5 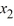 - 7
- 7 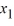
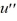 + 5
+ 5 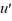 - 7 u = 0
- 7 u = 0A)
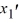 =
= 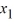 ,
, 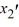 = 5
= 5 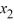 - 7
- 7 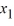
B)
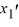 =
= 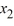 ,
, 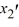 = 7
= 7 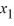 - 5
- 5 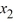
C)
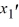 = -
= - 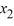 ,
, 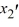 = 7
= 7 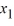 - 5
- 5 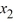
D)
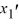 = -
= - 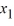 ,
, 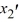 = 5
= 5 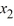 - 7
- 7 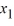
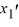 =
= 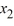 ,
, 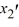 = 7
= 7 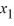 - 5
- 5 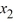
2
Into which of the following systems can this homogeneous third-order differential equation be transformed?
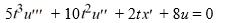
A)
B)
C)
D)
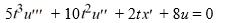
A)
B)
C)
D)
3
Transform this nonhomogeneous second-order initial value problem into an initial value problem comprised of two first-order differential equations:
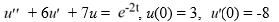
A)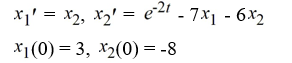
B)https://storage.examlex.com/TBW1042/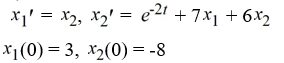 .
.
C)https://storage.examlex.com/TBW1042/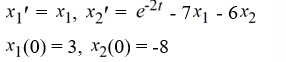 ..
..
D)https://storage.examlex.com/TBW1042/11eec281_8310_7efd_8720_6bc18854d758_TBW1042_11...
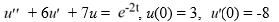
A)
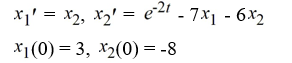
B)https://storage.examlex.com/TBW1042/
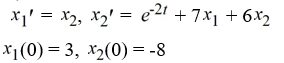 .
.C)https://storage.examlex.com/TBW1042/
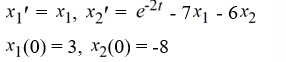 ..
..D)https://storage.examlex.com/TBW1042/11eec281_8310_7efd_8720_6bc18854d758_TBW1042_11...
4
Consider this system of first-order differential equations:
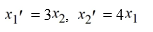
(i) Transform this system into a second-order differential equation whose solution is X1 .
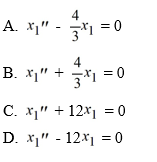
(ii) Find the general solution of the differential equation in part (i).
(iii) Use your solution in (ii) to now find X2.
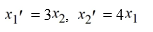
(i) Transform this system into a second-order differential equation whose solution is X1 .
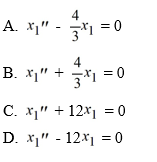
(ii) Find the general solution of the differential equation in part (i).
(iii) Use your solution in (ii) to now find X2.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
5
Consider this system of first-order differential equations:
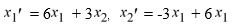
Transform this system into a second-order differential equation whose solution is X2 .
A)
B)
C)
D)
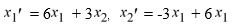
Transform this system into a second-order differential equation whose solution is X2 .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
6
Compute: ![<strong>Compute: </strong> A) \left[\begin{array}{ll}0 & -4 \\ 12 & -4\end{array}\right] B) \left[\begin{array}{ll}6 & 4 \\ 2 & 6\end{array}\right] C) \left[\begin{array}{ll}0 & 4 \\ 12 & 6\end{array}\right] D) \left[\begin{array}{ll}-12 & -8 \\ -4 & -12\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_703e_067f_9020_b77b190abade_TBW1042_11.jpg)
A)
B)
C)
D)
![<strong>Compute: </strong> A) \left[\begin{array}{ll}0 & -4 \\ 12 & -4\end{array}\right] B) \left[\begin{array}{ll}6 & 4 \\ 2 & 6\end{array}\right] C) \left[\begin{array}{ll}0 & 4 \\ 12 & 6\end{array}\right] D) \left[\begin{array}{ll}-12 & -8 \\ -4 & -12\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_703e_067f_9020_b77b190abade_TBW1042_11.jpg)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
7
Compute: ![<strong>Compute: </strong> A) \left[\begin{array}{ll}3 & -4 \\ 7 & -9 \\ -1 & -2\end{array}\right] B) \left[\begin{array}{cc}9 & 0 \\ 19 & -19 \\ -3 & -2\end{array}\right] C) \left[\begin{array}{ll}-3 & -8 \\ -5 & 1 \\ 1 & -2\end{array}\right] D) \left[\begin{array}{ll}-9 & -12 \\ -17 & 11 \\ 3 & -2\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_703e_0681_9020_b3c6fbdc89e1_TBW1042_11.jpg)
A)
B)
C)
D)
![<strong>Compute: </strong> A) \left[\begin{array}{ll}3 & -4 \\ 7 & -9 \\ -1 & -2\end{array}\right] B) \left[\begin{array}{cc}9 & 0 \\ 19 & -19 \\ -3 & -2\end{array}\right] C) \left[\begin{array}{ll}-3 & -8 \\ -5 & 1 \\ 1 & -2\end{array}\right] D) \left[\begin{array}{ll}-9 & -12 \\ -17 & 11 \\ 3 & -2\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_703e_0681_9020_b3c6fbdc89e1_TBW1042_11.jpg)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
8
Consider these matrices:
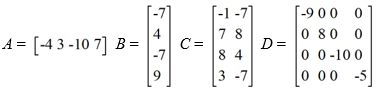
Which of the following matrices are defined? Select all that apply.
A) AB
B)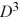
C) BA
D) AC
E) DC
F) BD
G) A + B
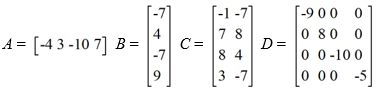
Which of the following matrices are defined? Select all that apply.
A) AB
B)
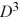
C) BA
D) AC
E) DC
F) BD
G) A + B

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
9
Consider the matrix ![<strong>Consider the matrix </strong> A) \left[\begin{array}{lllll}24 & -6 & -3 & -27 & 21 \\ 9 & -15 & -15 & 6 & 15\end{array}\right] B) \left[\begin{array}{cc}8 & 3 \\ -2 & -5 \\ -1 & -5 \\ -9 & 2 \\ 7 & 5\end{array}\right] C) \left[\begin{array}{ll}24 & 9 \\ -6 & -15 \\ -3 & -15 \\ -27 & 6 \\ 21 & 15\end{array}\right] D) \left[\begin{array}{ll}21 & 15 \\ -27 & 6 \\ -3 & -15 \\ -6 & -15 \\ 24 & 9\end{array}\right] E) \left[\begin{array}{ll}9 & 24 \\ -15 & -6 \\ -15 & -3 \\ 6 & -27 \\ 15 & 21\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_703e_2d95_9020_e135e73a5f70_TBW1042_11.jpg)
A)
B)
C)
D)
E)
![<strong>Consider the matrix </strong> A) \left[\begin{array}{lllll}24 & -6 & -3 & -27 & 21 \\ 9 & -15 & -15 & 6 & 15\end{array}\right] B) \left[\begin{array}{cc}8 & 3 \\ -2 & -5 \\ -1 & -5 \\ -9 & 2 \\ 7 & 5\end{array}\right] C) \left[\begin{array}{ll}24 & 9 \\ -6 & -15 \\ -3 & -15 \\ -27 & 6 \\ 21 & 15\end{array}\right] D) \left[\begin{array}{ll}21 & 15 \\ -27 & 6 \\ -3 & -15 \\ -6 & -15 \\ 24 & 9\end{array}\right] E) \left[\begin{array}{ll}9 & 24 \\ -15 & -6 \\ -15 & -3 \\ 6 & -27 \\ 15 & 21\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_703e_2d95_9020_e135e73a5f70_TBW1042_11.jpg)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
10
If A is an 2 × 4 matrix and B is an 4 × 9 matrix, then:
A) BA is defined and has order 2 × 9.
B) BA is defined and has order 9 × 2.
C) AB is defined and has order 9 × 2.
D) AB is defined and has order 2 × 9.
E) Neither AB nor BA is defined.
A) BA is defined and has order 2 × 9.
B) BA is defined and has order 9 × 2.
C) AB is defined and has order 9 × 2.
D) AB is defined and has order 2 × 9.
E) Neither AB nor BA is defined.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
11
Consider these matrices:
D =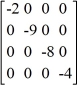 E =
E = 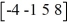
Compute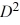
D =
 E =
E = 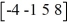
Compute
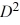

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
12
Consider these matrices:
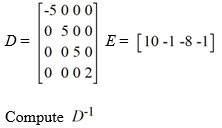
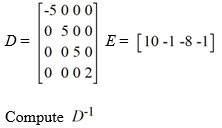

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
13
Consider these matrices:
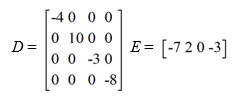
Compute ED
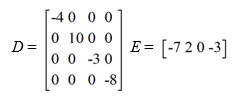
Compute ED

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
14
Consider the matrix function
A(t) =![<strong>Consider the matrix function A(t) = Compute (t).</strong> A) \left[\begin{array}{ll}-2 \cos (2 t) & 5 \sin (5 t) \\ 5 \sin (5 t) & 2 \cos (2 t)\end{array}\right] B) \left[\begin{array}{l}2 \cos (2 t)-5 \sin (5 t) \\ -5 \sin (5 t)-2 \cos (2 t)\end{array}\right] C) \left[\begin{array}{ll}\cos (2 t) & -\sin (5 t) \\ -\sin (5 t) & -\cos (2 t)\end{array}\right] D) \left[\begin{array}{ll}-\cos (2 t) & \sin (5 t) \\ \sin (5 t) & \cos (2 t)\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_703e_54af_9020_e91fe4ed021b_TBW1042_11.jpg)
Compute![<strong>Consider the matrix function A(t) = Compute (t).</strong> A) \left[\begin{array}{ll}-2 \cos (2 t) & 5 \sin (5 t) \\ 5 \sin (5 t) & 2 \cos (2 t)\end{array}\right] B) \left[\begin{array}{l}2 \cos (2 t)-5 \sin (5 t) \\ -5 \sin (5 t)-2 \cos (2 t)\end{array}\right] C) \left[\begin{array}{ll}\cos (2 t) & -\sin (5 t) \\ -\sin (5 t) & -\cos (2 t)\end{array}\right] D) \left[\begin{array}{ll}-\cos (2 t) & \sin (5 t) \\ \sin (5 t) & \cos (2 t)\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_703e_54b0_9020_c1f777ec8f96_TBW1042_11.jpg) (t).
(t).
A)
B)
C)
D)
A(t) =
![<strong>Consider the matrix function A(t) = Compute (t).</strong> A) \left[\begin{array}{ll}-2 \cos (2 t) & 5 \sin (5 t) \\ 5 \sin (5 t) & 2 \cos (2 t)\end{array}\right] B) \left[\begin{array}{l}2 \cos (2 t)-5 \sin (5 t) \\ -5 \sin (5 t)-2 \cos (2 t)\end{array}\right] C) \left[\begin{array}{ll}\cos (2 t) & -\sin (5 t) \\ -\sin (5 t) & -\cos (2 t)\end{array}\right] D) \left[\begin{array}{ll}-\cos (2 t) & \sin (5 t) \\ \sin (5 t) & \cos (2 t)\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_703e_54af_9020_e91fe4ed021b_TBW1042_11.jpg)
Compute
![<strong>Consider the matrix function A(t) = Compute (t).</strong> A) \left[\begin{array}{ll}-2 \cos (2 t) & 5 \sin (5 t) \\ 5 \sin (5 t) & 2 \cos (2 t)\end{array}\right] B) \left[\begin{array}{l}2 \cos (2 t)-5 \sin (5 t) \\ -5 \sin (5 t)-2 \cos (2 t)\end{array}\right] C) \left[\begin{array}{ll}\cos (2 t) & -\sin (5 t) \\ -\sin (5 t) & -\cos (2 t)\end{array}\right] D) \left[\begin{array}{ll}-\cos (2 t) & \sin (5 t) \\ \sin (5 t) & \cos (2 t)\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_703e_54b0_9020_c1f777ec8f96_TBW1042_11.jpg) (t).
(t).A)
B)
C)
D)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
15
Consider the matrix function A(t) ![<strong>Consider the matrix function A(t) Compute </strong> A) \left[\begin{array}{ll}-2 \cos (2 t) & -5 \sin (5 t) \\ -5 \sin (5 t) & 2 \cos (2 t)\end{array}\right] B) \frac{1}{4 \cos ^{2}(2 t)+25 \sin ^{2}(5 t)}\left[\begin{array}{ll}-2 \cos (2 t) & -5 \sin (5 t) \\ -5 \sin (5 t) & 2 \cos (2 t)\end{array}\right] C) \left[\begin{array}{ccc}-2 \cos (2 t) & 5 \sin (5 t) \\ 5 \sin (5 t) & 2 \cos (2 t)\end{array}\right] D) \frac{1}{4 \cos ^{2}(2 t)+25 \sin ^{2}(5 t)}\left[\begin{array}{ll}-2 \cos (2 t) & 5 \sin (5 t) \\ 5 \sin (5 t) & 2 \cos (2 t)\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_703e_54b2_9020_b55bb04f61b2_TBW1042_11.jpg) Compute
Compute ![<strong>Consider the matrix function A(t) Compute </strong> A) \left[\begin{array}{ll}-2 \cos (2 t) & -5 \sin (5 t) \\ -5 \sin (5 t) & 2 \cos (2 t)\end{array}\right] B) \frac{1}{4 \cos ^{2}(2 t)+25 \sin ^{2}(5 t)}\left[\begin{array}{ll}-2 \cos (2 t) & -5 \sin (5 t) \\ -5 \sin (5 t) & 2 \cos (2 t)\end{array}\right] C) \left[\begin{array}{ccc}-2 \cos (2 t) & 5 \sin (5 t) \\ 5 \sin (5 t) & 2 \cos (2 t)\end{array}\right] D) \frac{1}{4 \cos ^{2}(2 t)+25 \sin ^{2}(5 t)}\left[\begin{array}{ll}-2 \cos (2 t) & 5 \sin (5 t) \\ 5 \sin (5 t) & 2 \cos (2 t)\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_703e_54b3_9020_7f2651805148_TBW1042_11.jpg)
A)
B)
C)
D)
![<strong>Consider the matrix function A(t) Compute </strong> A) \left[\begin{array}{ll}-2 \cos (2 t) & -5 \sin (5 t) \\ -5 \sin (5 t) & 2 \cos (2 t)\end{array}\right] B) \frac{1}{4 \cos ^{2}(2 t)+25 \sin ^{2}(5 t)}\left[\begin{array}{ll}-2 \cos (2 t) & -5 \sin (5 t) \\ -5 \sin (5 t) & 2 \cos (2 t)\end{array}\right] C) \left[\begin{array}{ccc}-2 \cos (2 t) & 5 \sin (5 t) \\ 5 \sin (5 t) & 2 \cos (2 t)\end{array}\right] D) \frac{1}{4 \cos ^{2}(2 t)+25 \sin ^{2}(5 t)}\left[\begin{array}{ll}-2 \cos (2 t) & 5 \sin (5 t) \\ 5 \sin (5 t) & 2 \cos (2 t)\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_703e_54b2_9020_b55bb04f61b2_TBW1042_11.jpg) Compute
Compute ![<strong>Consider the matrix function A(t) Compute </strong> A) \left[\begin{array}{ll}-2 \cos (2 t) & -5 \sin (5 t) \\ -5 \sin (5 t) & 2 \cos (2 t)\end{array}\right] B) \frac{1}{4 \cos ^{2}(2 t)+25 \sin ^{2}(5 t)}\left[\begin{array}{ll}-2 \cos (2 t) & -5 \sin (5 t) \\ -5 \sin (5 t) & 2 \cos (2 t)\end{array}\right] C) \left[\begin{array}{ccc}-2 \cos (2 t) & 5 \sin (5 t) \\ 5 \sin (5 t) & 2 \cos (2 t)\end{array}\right] D) \frac{1}{4 \cos ^{2}(2 t)+25 \sin ^{2}(5 t)}\left[\begin{array}{ll}-2 \cos (2 t) & 5 \sin (5 t) \\ 5 \sin (5 t) & 2 \cos (2 t)\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_703e_54b3_9020_7f2651805148_TBW1042_11.jpg)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
16
Consider the matrix function 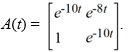 .
.
Compute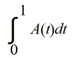
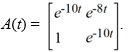 .
.Compute
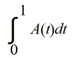

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
17
Consider the matrix 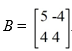 Compute B-1
Compute B-1
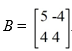 Compute B-1
Compute B-1
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
18
Consider the following system of linear equations:
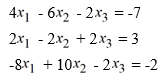
What is the augmented matrix for this system?
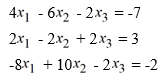
What is the augmented matrix for this system?

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
19
Consider the following system of linear equations:
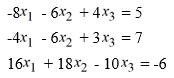
Reduce the augmented matrix of this system to echelon form.
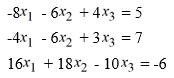
Reduce the augmented matrix of this system to echelon form.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
20
Consider the following system of linear equations:
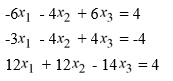
The system is inconsistent.
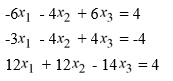
The system is inconsistent.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
21
Consider the following system of linear equations:
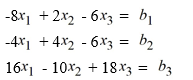
Find a condition involving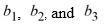 that ensures the system has infinitely many solutions.
that ensures the system has infinitely many solutions.
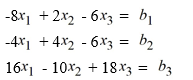
Find a condition involving
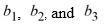 that ensures the system has infinitely many solutions.
that ensures the system has infinitely many solutions.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
22
Consider this set of vectors: 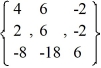 Which of these statements is true?
Which of these statements is true?
A) The vectors in this set are linearly independent.
B) The vectors in this set are linearly dependent.
C) The system Ax = 0, where A =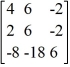 , has only the solution x = 0.
, has only the solution x = 0.
D) The system Ax = 0, where A =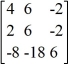 , is inconsistent.
, is inconsistent.
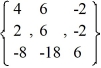 Which of these statements is true?
Which of these statements is true?A) The vectors in this set are linearly independent.
B) The vectors in this set are linearly dependent.
C) The system Ax = 0, where A =
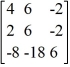 , has only the solution x = 0.
, has only the solution x = 0.D) The system Ax = 0, where A =
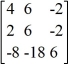 , is inconsistent.
, is inconsistent.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
23
Are the vectors u1 , u2 , and u3 linearly independent or linearly dependent? If they are linearly dependent, identify appropriate constants A, B, and C for which A u1 + Bu2 +Cu3 = 0
that demonstrates this fact.
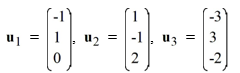
that demonstrates this fact.
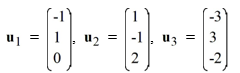

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
24
Are the vectors u1 , u2 , u3 , and u4 linearly independent or linearly dependent? If they are linearly dependent, identify appropriate constants A, B, C, and D for which A u1 + Bu2 +Cu3 +Du3 = 0 for which that demonstrates this fact.
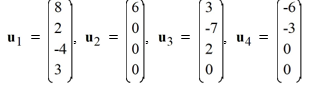
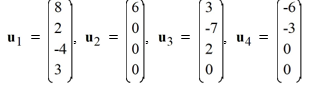

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
25
If = 0 is an eigenvalue of a 5 × 5 matrix A, then A is not invertible.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
26
Given that = 1 is an eigenvalue of the matrix B = 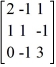 , which of the following statements is true regarding the eigenvector of B associated with this eigenvalue = 1?
, which of the following statements is true regarding the eigenvector of B associated with this eigenvalue = 1?
A)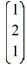 is the only eigenvector of B associated with the eigenvalue = 1.
is the only eigenvector of B associated with the eigenvalue = 1.
B) is an eigenvector of B, for any nonzero real constant , associated with the eigenvalue = 1.
is an eigenvector of B, for any nonzero real constant , associated with the eigenvalue = 1.
C) is an eigenvector of B, for any nonzero real constant , associated with the eigenvalue = 1.
is an eigenvector of B, for any nonzero real constant , associated with the eigenvalue = 1.
D) is the only eigenvector of B associated with the eigenvalue = 1.
is the only eigenvector of B associated with the eigenvalue = 1.
 , which of the following statements is true regarding the eigenvector of B associated with this eigenvalue = 1?
, which of the following statements is true regarding the eigenvector of B associated with this eigenvalue = 1?A)
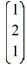 is the only eigenvector of B associated with the eigenvalue = 1.
is the only eigenvector of B associated with the eigenvalue = 1.B)
 is an eigenvector of B, for any nonzero real constant , associated with the eigenvalue = 1.
is an eigenvector of B, for any nonzero real constant , associated with the eigenvalue = 1.C)
 is an eigenvector of B, for any nonzero real constant , associated with the eigenvalue = 1.
is an eigenvector of B, for any nonzero real constant , associated with the eigenvalue = 1.D)
 is the only eigenvector of B associated with the eigenvalue = 1.
is the only eigenvector of B associated with the eigenvalue = 1.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the matrix 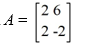
Which of these is a complete list of eigenvalue-eigenvector pairs of A?
A)
B)
C)
D)
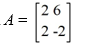
Which of these is a complete list of eigenvalue-eigenvector pairs of A?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
28
Consider a system of homogeneous first-order linear differential equations of the form 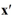 = Ax, where A is a 2 × 2 constant matrix.
= Ax, where A is a 2 × 2 constant matrix. 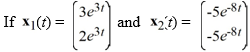 are solutions of this system, which of the following must also be solutions of this system? Select all that apply.
are solutions of this system, which of the following must also be solutions of this system? Select all that apply.
A)
B)
C)
D)
E)
F)
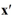 = Ax, where A is a 2 × 2 constant matrix.
= Ax, where A is a 2 × 2 constant matrix. 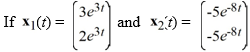 are solutions of this system, which of the following must also be solutions of this system? Select all that apply.
are solutions of this system, which of the following must also be solutions of this system? Select all that apply.A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
29
Consider the first-order homogeneous system of linear differential equations ![<strong>Consider the first-order homogeneous system of linear differential equations and the following three vector functions: Which of the following statements are true? Select all that apply.</strong> A) {X<sub>1</sub>,X<sub>2</sub> ,X<sub>3</sub> } is a fundamental set of solutions for this system. B) W [X<sub>1</sub>(t), X<sub>2</sub>(t)] ? 0 for every real number t. C) X<sub>1</sub> and X<sub>2</sub> are linearly dependent. D) 6X<sub>1</sub> + 4X<sub>2</sub> + 3X<sub>3</sub> is a solution of this system. E) {X<sub>1</sub>, X<sub>2</sub>} is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_ca02_9020_2df2565f59e6_TBW1042_11.jpg) and the following three vector functions:
and the following three vector functions:
![<strong>Consider the first-order homogeneous system of linear differential equations and the following three vector functions: Which of the following statements are true? Select all that apply.</strong> A) {X<sub>1</sub>,X<sub>2</sub> ,X<sub>3</sub> } is a fundamental set of solutions for this system. B) W [X<sub>1</sub>(t), X<sub>2</sub>(t)] ? 0 for every real number t. C) X<sub>1</sub> and X<sub>2</sub> are linearly dependent. D) 6X<sub>1</sub> + 4X<sub>2</sub> + 3X<sub>3</sub> is a solution of this system. E) {X<sub>1</sub>, X<sub>2</sub>} is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_ca03_9020_73d7fc62c030_TBW1042_00.jpg)
Which of the following statements are true? Select all that apply.
A) {X1,X2 ,X3 } is a fundamental set of solutions for this system.
B) W [X1(t), X2(t)] ? 0 for every real number t.
C) X1 and X2 are linearly dependent.
D) 6X1 + 4X2 + 3X3 is a solution of this system.
E) {X1, X2} is a fundamental set of solutions for this system.
![<strong>Consider the first-order homogeneous system of linear differential equations and the following three vector functions: Which of the following statements are true? Select all that apply.</strong> A) {X<sub>1</sub>,X<sub>2</sub> ,X<sub>3</sub> } is a fundamental set of solutions for this system. B) W [X<sub>1</sub>(t), X<sub>2</sub>(t)] ? 0 for every real number t. C) X<sub>1</sub> and X<sub>2</sub> are linearly dependent. D) 6X<sub>1</sub> + 4X<sub>2</sub> + 3X<sub>3</sub> is a solution of this system. E) {X<sub>1</sub>, X<sub>2</sub>} is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_ca02_9020_2df2565f59e6_TBW1042_11.jpg) and the following three vector functions:
and the following three vector functions:![<strong>Consider the first-order homogeneous system of linear differential equations and the following three vector functions: Which of the following statements are true? Select all that apply.</strong> A) {X<sub>1</sub>,X<sub>2</sub> ,X<sub>3</sub> } is a fundamental set of solutions for this system. B) W [X<sub>1</sub>(t), X<sub>2</sub>(t)] ? 0 for every real number t. C) X<sub>1</sub> and X<sub>2</sub> are linearly dependent. D) 6X<sub>1</sub> + 4X<sub>2</sub> + 3X<sub>3</sub> is a solution of this system. E) {X<sub>1</sub>, X<sub>2</sub>} is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_ca03_9020_73d7fc62c030_TBW1042_00.jpg)
Which of the following statements are true? Select all that apply.
A) {X1,X2 ,X3 } is a fundamental set of solutions for this system.
B) W [X1(t), X2(t)] ? 0 for every real number t.
C) X1 and X2 are linearly dependent.
D) 6X1 + 4X2 + 3X3 is a solution of this system.
E) {X1, X2} is a fundamental set of solutions for this system.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
30
Consider the first-order homogeneous system of linear differential equations
![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f114_9020_f9f40a0ba094_TBW1042_11.jpg)
And the following four vector functions:
![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f115_9020_31940a18ecfe_TBW1042_00.jpg)
Which of the following statements are true? Select all that apply.
A)![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f116_9020_3d8caa802011_TBW1042_11.jpg) is a solution of this system, for all real numbers C1 ,C2 ,C3 , and C4 .
is a solution of this system, for all real numbers C1 ,C2 ,C3 , and C4 .
B) W [![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f117_9020_cfed8ea2218f_TBW1042_11.jpg) (t),
(t), ![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f118_9020_935f101fc5c1_TBW1042_11.jpg) (t)] ? 0 for every real number t.
(t)] ? 0 for every real number t.
C) 5.5![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f119_9020_fb7e2a83f916_TBW1042_11.jpg) + 4.5
+ 4.5 ![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f11a_9020_9d392d167189_TBW1042_11.jpg) + C is a solution of this system, for any real number C.
+ C is a solution of this system, for any real number C.
D) 4![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f11b_9020_a1170b212c80_TBW1042_11.jpg) is a solution of this system.
is a solution of this system.
E) {![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f11c_9020_5bb79c6bf120_TBW1042_11.jpg) ,
, ![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f11d_9020_7b191d75324d_TBW1042_11.jpg) } is a fundamental set of solutions for this system.
} is a fundamental set of solutions for this system.
![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f114_9020_f9f40a0ba094_TBW1042_11.jpg)
And the following four vector functions:
![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f115_9020_31940a18ecfe_TBW1042_00.jpg)
Which of the following statements are true? Select all that apply.
A)
![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f116_9020_3d8caa802011_TBW1042_11.jpg) is a solution of this system, for all real numbers C1 ,C2 ,C3 , and C4 .
is a solution of this system, for all real numbers C1 ,C2 ,C3 , and C4 .B) W [
![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f117_9020_cfed8ea2218f_TBW1042_11.jpg) (t),
(t), ![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f118_9020_935f101fc5c1_TBW1042_11.jpg) (t)] ? 0 for every real number t.
(t)] ? 0 for every real number t.C) 5.5
![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f119_9020_fb7e2a83f916_TBW1042_11.jpg) + 4.5
+ 4.5 ![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f11a_9020_9d392d167189_TBW1042_11.jpg) + C is a solution of this system, for any real number C.
+ C is a solution of this system, for any real number C.D) 4
![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f11b_9020_a1170b212c80_TBW1042_11.jpg) is a solution of this system.
is a solution of this system.E) {
![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f11c_9020_5bb79c6bf120_TBW1042_11.jpg) ,
, ![<strong>Consider the first-order homogeneous system of linear differential equations And the following four vector functions: Which of the following statements are true? Select all that apply.</strong> A) is a solution of this system, for all real numbers C<sub>1</sub> ,C<sub>2</sub> ,C<sub>3</sub> , and C<sub>4</sub> . B) W [ (t), (t)] ? 0 for every real number t. C) 5.5 + 4.5 + C is a solution of this system, for any real number C. D) 4 is a solution of this system. E) { , } is a fundamental set of solutions for this system.](https://storage.examlex.com/TBW1042/11eeb833_703e_f11d_9020_7b191d75324d_TBW1042_11.jpg) } is a fundamental set of solutions for this system.
} is a fundamental set of solutions for this system.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
31
Consider the first-order homogeneous system of linear differential equations
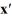 =
= 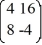 x
x
Determine the eigenvalue-eigenvector pairs of this system.
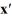 =
= 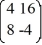 x
xDetermine the eigenvalue-eigenvector pairs of this system.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
32
Consider the first-order homogeneous system of linear differential equations
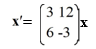
What is the general solution of this system?
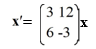
What is the general solution of this system?

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
33
Consider the first-order homogeneous system of linear differential equations
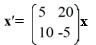
If the system were equipped with the initial condition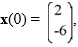 what is the particular solution of the system?
what is the particular solution of the system?
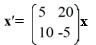
If the system were equipped with the initial condition
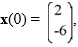 what is the particular solution of the system?
what is the particular solution of the system?
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
34
Consider the first-order homogeneous system of linear differential equations
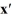 =
= 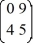 x
x
Select all of the correct eigenvalue-eigenvector pairs from the following choices.
A)
B)
C)
D)
E)
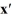 =
=  x
xSelect all of the correct eigenvalue-eigenvector pairs from the following choices.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
35
Consider the first-order homogeneous system of linear differential equations
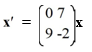
Which of these is the general solution of the system? Here, C1 and C2 are arbitrary real constants.
A)
B)
C)
D)
E)
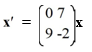
Which of these is the general solution of the system? Here, C1 and C2 are arbitrary real constants.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
36
Consider the first-order homogeneous system of linear differential equations
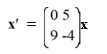
The origin is a saddle point.
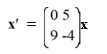
The origin is a saddle point.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
37
Consider the first-order homogeneous system of linear differential equations
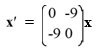
Select all of the correct eigenvalue-eigenvector pairs from the following choices.
A)
B)
C)
D)
E)
F)
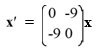
Select all of the correct eigenvalue-eigenvector pairs from the following choices.
A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
38
Consider the first-order homogeneous system of linear differential equations 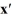 =
= 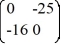 x
x
Which of these is the genreal solution of the system? Here,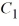 and
and 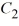 are arbitrary real constants.
are arbitrary real constants.
A)
B)
C)
D)
E)
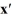 =
= 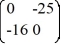 x
xWhich of these is the genreal solution of the system? Here,
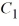 and
and 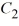 are arbitrary real constants.
are arbitrary real constants.A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
39
Consider the first-order homogeneous system of linear differential equations
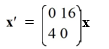
The origin is a node.
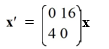
The origin is a node.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
40
Consider the first-order homogeneous system of linear differential equations
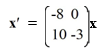
Select all of the correct eigenvalue-eigenvector pairs from the following choices.
A)
B)
C)
D)
E)
F)
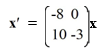
Select all of the correct eigenvalue-eigenvector pairs from the following choices.
A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
41
Consider the first-order homogeneous system of linear differential equations
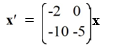
Which of these is the general solution of the system? Here, C1 and C2 are arbitrary real constants.
A)
B)
C)
D)
E)
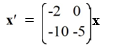
Which of these is the general solution of the system? Here, C1 and C2 are arbitrary real constants.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
42
Consider the first-order homogeneous system of linear differential equations
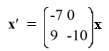
The origin is a node.
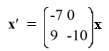
The origin is a node.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
43
Consider the first-order homogeneous system of linear differential equations
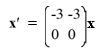
Select all of the eigenvalue-eigenvector pairs from the following choices.
A)
B)
C)
D)
E)
F)
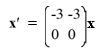
Select all of the eigenvalue-eigenvector pairs from the following choices.
A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
44
Consider the first-order homogeneous system of linear differential equations
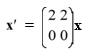
Which of these is the general solution of the system? Here, C1 and C2 are arbitrary real constants.
A)
B)
C)
D)
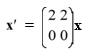
Which of these is the general solution of the system? Here, C1 and C2 are arbitrary real constants.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
45
Consider the first-order homogeneous system of linear differential equations
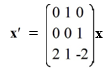
What is the general solution of this system?
A)
B)
C)
D)
E)
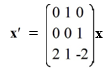
What is the general solution of this system?
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
46
Consider the first-order homogeneous system of linear differential equations
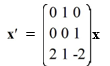
If the system were equipped with the initial condition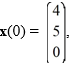 what is the particular solution of the system?
what is the particular solution of the system?
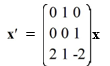
If the system were equipped with the initial condition
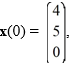 what is the particular solution of the system?
what is the particular solution of the system?
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
47
Suppose Tank A contains 50 gallons of water in which 30 ounces of salt are dissolved, and tank B contains 35 gallons of water in which 60 ounces of salt are dissolved. The following conditions also hold:
• Water with salt concentration of 1.6 ounces per gallon flows into Tank A at a rate of 1.8 gallons per minute.
• Water with salt concentration of 3.1 ounces per gallon flows into Tank B at a rate of 1.3 gallons per minute.
• Water flows from Tank A to Tank B at a rate of 1.8 gallons per minute.
• Water flows from Tank B to Tank A at a rate of 0.65 gallons per minute.
• Water drains from Tank B at a rate of 0.65 gallons per minute.
Set up a system of equations governing the amount of salt in Tank A,X A (t), and the amount of salt in tank B, X B (t), at any time t.
• Water with salt concentration of 1.6 ounces per gallon flows into Tank A at a rate of 1.8 gallons per minute.
• Water with salt concentration of 3.1 ounces per gallon flows into Tank B at a rate of 1.3 gallons per minute.
• Water flows from Tank A to Tank B at a rate of 1.8 gallons per minute.
• Water flows from Tank B to Tank A at a rate of 0.65 gallons per minute.
• Water drains from Tank B at a rate of 0.65 gallons per minute.
Set up a system of equations governing the amount of salt in Tank A,X A (t), and the amount of salt in tank B, X B (t), at any time t.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
48
Each of the following is the general solution of a system of differential equations. For which one(s) is the origin a node? Select all that apply.
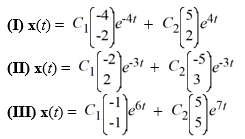
A) I
B) II
C) III
D) None of them
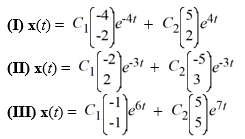
A) I
B) II
C) III
D) None of them

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
49
Consider the first-order homogeneous system of linear differential equations
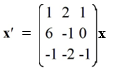
Determine a fundamental set of solutions for this system.
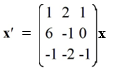
Determine a fundamental set of solutions for this system.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
50
Consider the first-order homogeneous system of linear differential equations
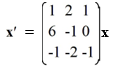
What is the general solution of this system?
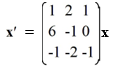
What is the general solution of this system?

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
51
Consider the first-order homogeneous system of linear differential equations
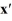 =
= 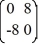 x
x
Which of these are eigenvalues for this system? Select all that apply.
A) -8
B) 8
C) 0
D) 8i
E) -8i
F) 64
G) -64
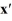 =
= 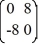 x
xWhich of these are eigenvalues for this system? Select all that apply.
A) -8
B) 8
C) 0
D) 8i
E) -8i
F) 64
G) -64

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
52
Consider the first-order homogeneous system of linear differential equations
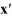 =
= 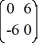 x
x
Which of these is a fundamental set of solutions for this system?
A)
B)
C)
D)
E)
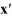 =
= 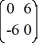 x
xWhich of these is a fundamental set of solutions for this system?
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
53
Consider the first-order homogeneous system of linear differential equations
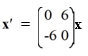
Which of these is an accurate description of the solution trajectories of the phase portrait for this system?
A) The trajectories spiral towards the origin as t .
B) The trajectories are concentric circles centered at the origin.
C) The trajectories spiral away from the origin as t .
D) The trajectories are line segments that approach the origin as t .
E) The origin is a saddle point.
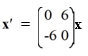
Which of these is an accurate description of the solution trajectories of the phase portrait for this system?
A) The trajectories spiral towards the origin as t .
B) The trajectories are concentric circles centered at the origin.
C) The trajectories spiral away from the origin as t .
D) The trajectories are line segments that approach the origin as t .
E) The origin is a saddle point.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
54
Consider the first-order homogeneous system of linear differential equations
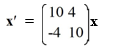
Which of these are eigenvalues for this system? Select all that apply.
A) 10
B) 4
C) -4i
D) 10 + 4i
E) 4i
F) 10 - 4i
G) 4 + 10i
H) 4 - 10i
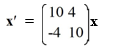
Which of these are eigenvalues for this system? Select all that apply.
A) 10
B) 4
C) -4i
D) 10 + 4i
E) 4i
F) 10 - 4i
G) 4 + 10i
H) 4 - 10i

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
55
Consider the first-order homogeneous system of linear differential equations
![<strong>Consider the first-order homogeneous system of linear differential equations What is the general solution of this system? Here, and are arbitrary real constants.</strong> A) \mathbf{x}(t)=C_{1} e^{-3 t}\left(\begin{array}{l}\sin (8 t) \\ \cos (8 t)\end{array}\right)+C_{2} e^{-3 t}\left[\begin{array}{l}-\cos (8 t) \\ \sin (8 t)\end{array}\right) B) \mathbf{x}(t)=C_{1} e^{3 t}\left(\begin{array}{l}\sin (8 t) \\ \cos (8 t)\end{array}\right)+C_{2} e^{3 t}\left(\begin{array}{l}-\cos (8 t) \\ \sin (8 t)\end{array}\right) C) \mathbf{x}(t)=C_{1} e^{-8 t}\left(\begin{array}{l}\sin (3 t) \\ \cos (3 t)\end{array}\right]+C_{2} e^{-8 t}\left(\begin{array}{l}-\cos (3 t) \\ \sin (3 t)\end{array}\right) D) \mathbf{x}(t)=C_{1} e^{8 t}\left(\begin{array}{l}\sin (3 t) \\ \cos (3 t)\end{array}\right)+C_{2} e^{8 t}\left\{\begin{array}{l}-\cos (3 t) \\ \sin (3 t)\end{array}\right)](https://storage.examlex.com/TBW1042/11eeb833_703f_dbaf_9020_0b8071cd2d29_TBW1042_00.jpg)
What is the general solution of this system? Here,![<strong>Consider the first-order homogeneous system of linear differential equations What is the general solution of this system? Here, and are arbitrary real constants.</strong> A) \mathbf{x}(t)=C_{1} e^{-3 t}\left(\begin{array}{l}\sin (8 t) \\ \cos (8 t)\end{array}\right)+C_{2} e^{-3 t}\left[\begin{array}{l}-\cos (8 t) \\ \sin (8 t)\end{array}\right) B) \mathbf{x}(t)=C_{1} e^{3 t}\left(\begin{array}{l}\sin (8 t) \\ \cos (8 t)\end{array}\right)+C_{2} e^{3 t}\left(\begin{array}{l}-\cos (8 t) \\ \sin (8 t)\end{array}\right) C) \mathbf{x}(t)=C_{1} e^{-8 t}\left(\begin{array}{l}\sin (3 t) \\ \cos (3 t)\end{array}\right]+C_{2} e^{-8 t}\left(\begin{array}{l}-\cos (3 t) \\ \sin (3 t)\end{array}\right) D) \mathbf{x}(t)=C_{1} e^{8 t}\left(\begin{array}{l}\sin (3 t) \\ \cos (3 t)\end{array}\right)+C_{2} e^{8 t}\left\{\begin{array}{l}-\cos (3 t) \\ \sin (3 t)\end{array}\right)](https://storage.examlex.com/TBW1042/11eeb833_703f_dbb0_9020_03c448f0cd4c_TBW1042_11.jpg) and
and ![<strong>Consider the first-order homogeneous system of linear differential equations What is the general solution of this system? Here, and are arbitrary real constants.</strong> A) \mathbf{x}(t)=C_{1} e^{-3 t}\left(\begin{array}{l}\sin (8 t) \\ \cos (8 t)\end{array}\right)+C_{2} e^{-3 t}\left[\begin{array}{l}-\cos (8 t) \\ \sin (8 t)\end{array}\right) B) \mathbf{x}(t)=C_{1} e^{3 t}\left(\begin{array}{l}\sin (8 t) \\ \cos (8 t)\end{array}\right)+C_{2} e^{3 t}\left(\begin{array}{l}-\cos (8 t) \\ \sin (8 t)\end{array}\right) C) \mathbf{x}(t)=C_{1} e^{-8 t}\left(\begin{array}{l}\sin (3 t) \\ \cos (3 t)\end{array}\right]+C_{2} e^{-8 t}\left(\begin{array}{l}-\cos (3 t) \\ \sin (3 t)\end{array}\right) D) \mathbf{x}(t)=C_{1} e^{8 t}\left(\begin{array}{l}\sin (3 t) \\ \cos (3 t)\end{array}\right)+C_{2} e^{8 t}\left\{\begin{array}{l}-\cos (3 t) \\ \sin (3 t)\end{array}\right)](https://storage.examlex.com/TBW1042/11eeb833_703f_dbb1_9020_61560b928061_TBW1042_11.jpg) are arbitrary real constants.
are arbitrary real constants.
A)
B)
C)
D)
![<strong>Consider the first-order homogeneous system of linear differential equations What is the general solution of this system? Here, and are arbitrary real constants.</strong> A) \mathbf{x}(t)=C_{1} e^{-3 t}\left(\begin{array}{l}\sin (8 t) \\ \cos (8 t)\end{array}\right)+C_{2} e^{-3 t}\left[\begin{array}{l}-\cos (8 t) \\ \sin (8 t)\end{array}\right) B) \mathbf{x}(t)=C_{1} e^{3 t}\left(\begin{array}{l}\sin (8 t) \\ \cos (8 t)\end{array}\right)+C_{2} e^{3 t}\left(\begin{array}{l}-\cos (8 t) \\ \sin (8 t)\end{array}\right) C) \mathbf{x}(t)=C_{1} e^{-8 t}\left(\begin{array}{l}\sin (3 t) \\ \cos (3 t)\end{array}\right]+C_{2} e^{-8 t}\left(\begin{array}{l}-\cos (3 t) \\ \sin (3 t)\end{array}\right) D) \mathbf{x}(t)=C_{1} e^{8 t}\left(\begin{array}{l}\sin (3 t) \\ \cos (3 t)\end{array}\right)+C_{2} e^{8 t}\left\{\begin{array}{l}-\cos (3 t) \\ \sin (3 t)\end{array}\right)](https://storage.examlex.com/TBW1042/11eeb833_703f_dbaf_9020_0b8071cd2d29_TBW1042_00.jpg)
What is the general solution of this system? Here,
![<strong>Consider the first-order homogeneous system of linear differential equations What is the general solution of this system? Here, and are arbitrary real constants.</strong> A) \mathbf{x}(t)=C_{1} e^{-3 t}\left(\begin{array}{l}\sin (8 t) \\ \cos (8 t)\end{array}\right)+C_{2} e^{-3 t}\left[\begin{array}{l}-\cos (8 t) \\ \sin (8 t)\end{array}\right) B) \mathbf{x}(t)=C_{1} e^{3 t}\left(\begin{array}{l}\sin (8 t) \\ \cos (8 t)\end{array}\right)+C_{2} e^{3 t}\left(\begin{array}{l}-\cos (8 t) \\ \sin (8 t)\end{array}\right) C) \mathbf{x}(t)=C_{1} e^{-8 t}\left(\begin{array}{l}\sin (3 t) \\ \cos (3 t)\end{array}\right]+C_{2} e^{-8 t}\left(\begin{array}{l}-\cos (3 t) \\ \sin (3 t)\end{array}\right) D) \mathbf{x}(t)=C_{1} e^{8 t}\left(\begin{array}{l}\sin (3 t) \\ \cos (3 t)\end{array}\right)+C_{2} e^{8 t}\left\{\begin{array}{l}-\cos (3 t) \\ \sin (3 t)\end{array}\right)](https://storage.examlex.com/TBW1042/11eeb833_703f_dbb0_9020_03c448f0cd4c_TBW1042_11.jpg) and
and ![<strong>Consider the first-order homogeneous system of linear differential equations What is the general solution of this system? Here, and are arbitrary real constants.</strong> A) \mathbf{x}(t)=C_{1} e^{-3 t}\left(\begin{array}{l}\sin (8 t) \\ \cos (8 t)\end{array}\right)+C_{2} e^{-3 t}\left[\begin{array}{l}-\cos (8 t) \\ \sin (8 t)\end{array}\right) B) \mathbf{x}(t)=C_{1} e^{3 t}\left(\begin{array}{l}\sin (8 t) \\ \cos (8 t)\end{array}\right)+C_{2} e^{3 t}\left(\begin{array}{l}-\cos (8 t) \\ \sin (8 t)\end{array}\right) C) \mathbf{x}(t)=C_{1} e^{-8 t}\left(\begin{array}{l}\sin (3 t) \\ \cos (3 t)\end{array}\right]+C_{2} e^{-8 t}\left(\begin{array}{l}-\cos (3 t) \\ \sin (3 t)\end{array}\right) D) \mathbf{x}(t)=C_{1} e^{8 t}\left(\begin{array}{l}\sin (3 t) \\ \cos (3 t)\end{array}\right)+C_{2} e^{8 t}\left\{\begin{array}{l}-\cos (3 t) \\ \sin (3 t)\end{array}\right)](https://storage.examlex.com/TBW1042/11eeb833_703f_dbb1_9020_61560b928061_TBW1042_11.jpg) are arbitrary real constants.
are arbitrary real constants.A)
B)
C)
D)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
56
Consider the first-order homogeneous system of linear differential equations
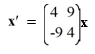
All solution trajectories spiral towards the origin as t .
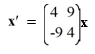
All solution trajectories spiral towards the origin as t .

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
57
Consider the first-order homogeneous system of linear differential equations
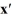 =
= 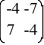 x
x
Which of these are eigenvalues for this system? Select all that apply.
A) -4 + 7i
B) 7
C) -7i
D) -4
E) 7i
F) 7 + 4i
G) 7 - 4i
H) -4 - 7i
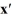 =
= 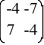 x
xWhich of these are eigenvalues for this system? Select all that apply.
A) -4 + 7i
B) 7
C) -7i
D) -4
E) 7i
F) 7 + 4i
G) 7 - 4i
H) -4 - 7i

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
58
Consider the first-order homogeneous system of linear differential equations
![<strong>Consider the first-order homogeneous system of linear differential equations What is the general solution of this system? Here, and are arbitrary real constants.</strong> A) \mathbf{x}(t)=C_{1} e^{-2 t}\left[\begin{array}{l}\sin (-8 t) \\ \cos (-8 t)\end{array}\right)+C_{2} e^{-2 t}\left[\begin{array}{l}-\cos (-8 t) \\ \sin (-8 t)\end{array}\right) B) \mathbf{x}(t)=C_{1} e^{8 t}\left(\begin{array}{l}\sin (2 t) \\ \cos (2 t)\end{array}\right)+C_{2} e^{8 t}\left(\begin{array}{l}-\cos (2 t) \\ \sin (2 t)\end{array}\right) C) \mathbf{x}(t)=C_{1} e^{-8 t}\left[\begin{array}{l}\sin (2 t) \\ \cos (2 t)\end{array}\right]+C_{2} e^{-8 t}\left[\begin{array}{l}-\cos (2 t) \\ \sin (2 t)\end{array}\right) D) \mathbf{x}(t)=C_{1} e^{2 t}\left(\begin{array}{l}\sin (-8 t) \\ \cos (-8 t)\end{array}\right)+C_{2} e^{2 t}\left[\begin{array}{l}-\cos (-8 t) \\ \sin (-8 t)\end{array}\right)](https://storage.examlex.com/TBW1042/11eeb833_703f_dbb6_9020_bde93c9d77e1_TBW1042_11.jpg)
What is the general solution of this system? Here,![<strong>Consider the first-order homogeneous system of linear differential equations What is the general solution of this system? Here, and are arbitrary real constants.</strong> A) \mathbf{x}(t)=C_{1} e^{-2 t}\left[\begin{array}{l}\sin (-8 t) \\ \cos (-8 t)\end{array}\right)+C_{2} e^{-2 t}\left[\begin{array}{l}-\cos (-8 t) \\ \sin (-8 t)\end{array}\right) B) \mathbf{x}(t)=C_{1} e^{8 t}\left(\begin{array}{l}\sin (2 t) \\ \cos (2 t)\end{array}\right)+C_{2} e^{8 t}\left(\begin{array}{l}-\cos (2 t) \\ \sin (2 t)\end{array}\right) C) \mathbf{x}(t)=C_{1} e^{-8 t}\left[\begin{array}{l}\sin (2 t) \\ \cos (2 t)\end{array}\right]+C_{2} e^{-8 t}\left[\begin{array}{l}-\cos (2 t) \\ \sin (2 t)\end{array}\right) D) \mathbf{x}(t)=C_{1} e^{2 t}\left(\begin{array}{l}\sin (-8 t) \\ \cos (-8 t)\end{array}\right)+C_{2} e^{2 t}\left[\begin{array}{l}-\cos (-8 t) \\ \sin (-8 t)\end{array}\right)](https://storage.examlex.com/TBW1042/11eeb833_703f_dbb7_9020_b13000a7831b_TBW1042_11.jpg) and
and ![<strong>Consider the first-order homogeneous system of linear differential equations What is the general solution of this system? Here, and are arbitrary real constants.</strong> A) \mathbf{x}(t)=C_{1} e^{-2 t}\left[\begin{array}{l}\sin (-8 t) \\ \cos (-8 t)\end{array}\right)+C_{2} e^{-2 t}\left[\begin{array}{l}-\cos (-8 t) \\ \sin (-8 t)\end{array}\right) B) \mathbf{x}(t)=C_{1} e^{8 t}\left(\begin{array}{l}\sin (2 t) \\ \cos (2 t)\end{array}\right)+C_{2} e^{8 t}\left(\begin{array}{l}-\cos (2 t) \\ \sin (2 t)\end{array}\right) C) \mathbf{x}(t)=C_{1} e^{-8 t}\left[\begin{array}{l}\sin (2 t) \\ \cos (2 t)\end{array}\right]+C_{2} e^{-8 t}\left[\begin{array}{l}-\cos (2 t) \\ \sin (2 t)\end{array}\right) D) \mathbf{x}(t)=C_{1} e^{2 t}\left(\begin{array}{l}\sin (-8 t) \\ \cos (-8 t)\end{array}\right)+C_{2} e^{2 t}\left[\begin{array}{l}-\cos (-8 t) \\ \sin (-8 t)\end{array}\right)](https://storage.examlex.com/TBW1042/11eeb833_7040_02c8_9020_6b9976bf74fd_TBW1042_11.jpg) are arbitrary real constants.
are arbitrary real constants.
A)
B)
C)
D)
![<strong>Consider the first-order homogeneous system of linear differential equations What is the general solution of this system? Here, and are arbitrary real constants.</strong> A) \mathbf{x}(t)=C_{1} e^{-2 t}\left[\begin{array}{l}\sin (-8 t) \\ \cos (-8 t)\end{array}\right)+C_{2} e^{-2 t}\left[\begin{array}{l}-\cos (-8 t) \\ \sin (-8 t)\end{array}\right) B) \mathbf{x}(t)=C_{1} e^{8 t}\left(\begin{array}{l}\sin (2 t) \\ \cos (2 t)\end{array}\right)+C_{2} e^{8 t}\left(\begin{array}{l}-\cos (2 t) \\ \sin (2 t)\end{array}\right) C) \mathbf{x}(t)=C_{1} e^{-8 t}\left[\begin{array}{l}\sin (2 t) \\ \cos (2 t)\end{array}\right]+C_{2} e^{-8 t}\left[\begin{array}{l}-\cos (2 t) \\ \sin (2 t)\end{array}\right) D) \mathbf{x}(t)=C_{1} e^{2 t}\left(\begin{array}{l}\sin (-8 t) \\ \cos (-8 t)\end{array}\right)+C_{2} e^{2 t}\left[\begin{array}{l}-\cos (-8 t) \\ \sin (-8 t)\end{array}\right)](https://storage.examlex.com/TBW1042/11eeb833_703f_dbb6_9020_bde93c9d77e1_TBW1042_11.jpg)
What is the general solution of this system? Here,
![<strong>Consider the first-order homogeneous system of linear differential equations What is the general solution of this system? Here, and are arbitrary real constants.</strong> A) \mathbf{x}(t)=C_{1} e^{-2 t}\left[\begin{array}{l}\sin (-8 t) \\ \cos (-8 t)\end{array}\right)+C_{2} e^{-2 t}\left[\begin{array}{l}-\cos (-8 t) \\ \sin (-8 t)\end{array}\right) B) \mathbf{x}(t)=C_{1} e^{8 t}\left(\begin{array}{l}\sin (2 t) \\ \cos (2 t)\end{array}\right)+C_{2} e^{8 t}\left(\begin{array}{l}-\cos (2 t) \\ \sin (2 t)\end{array}\right) C) \mathbf{x}(t)=C_{1} e^{-8 t}\left[\begin{array}{l}\sin (2 t) \\ \cos (2 t)\end{array}\right]+C_{2} e^{-8 t}\left[\begin{array}{l}-\cos (2 t) \\ \sin (2 t)\end{array}\right) D) \mathbf{x}(t)=C_{1} e^{2 t}\left(\begin{array}{l}\sin (-8 t) \\ \cos (-8 t)\end{array}\right)+C_{2} e^{2 t}\left[\begin{array}{l}-\cos (-8 t) \\ \sin (-8 t)\end{array}\right)](https://storage.examlex.com/TBW1042/11eeb833_703f_dbb7_9020_b13000a7831b_TBW1042_11.jpg) and
and ![<strong>Consider the first-order homogeneous system of linear differential equations What is the general solution of this system? Here, and are arbitrary real constants.</strong> A) \mathbf{x}(t)=C_{1} e^{-2 t}\left[\begin{array}{l}\sin (-8 t) \\ \cos (-8 t)\end{array}\right)+C_{2} e^{-2 t}\left[\begin{array}{l}-\cos (-8 t) \\ \sin (-8 t)\end{array}\right) B) \mathbf{x}(t)=C_{1} e^{8 t}\left(\begin{array}{l}\sin (2 t) \\ \cos (2 t)\end{array}\right)+C_{2} e^{8 t}\left(\begin{array}{l}-\cos (2 t) \\ \sin (2 t)\end{array}\right) C) \mathbf{x}(t)=C_{1} e^{-8 t}\left[\begin{array}{l}\sin (2 t) \\ \cos (2 t)\end{array}\right]+C_{2} e^{-8 t}\left[\begin{array}{l}-\cos (2 t) \\ \sin (2 t)\end{array}\right) D) \mathbf{x}(t)=C_{1} e^{2 t}\left(\begin{array}{l}\sin (-8 t) \\ \cos (-8 t)\end{array}\right)+C_{2} e^{2 t}\left[\begin{array}{l}-\cos (-8 t) \\ \sin (-8 t)\end{array}\right)](https://storage.examlex.com/TBW1042/11eeb833_7040_02c8_9020_6b9976bf74fd_TBW1042_11.jpg) are arbitrary real constants.
are arbitrary real constants.A)
B)
C)
D)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
59
Consider the first-order homogeneous system of linear differential equations
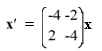
Which of the following is an accurate statement regarding the behavior of the solution trajectories of this system as t ?
A) All trajectories spiral towards the origin as t .
B) All trajectories spiral away from the origin as t .
C) The trajectories are concentric circles centered at the origin.
D) The trajectories are line segments that approach the origin as t .
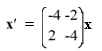
Which of the following is an accurate statement regarding the behavior of the solution trajectories of this system as t ?
A) All trajectories spiral towards the origin as t .
B) All trajectories spiral away from the origin as t .
C) The trajectories are concentric circles centered at the origin.
D) The trajectories are line segments that approach the origin as t .

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
60
Consider the first-order homogeneous system of linear differential equations
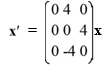
Which of these are eigenvalues for this system? Select all that apply.
A) 0
B) -16
C) 4i
D) -4i
E) -4
F) 4
G) 16
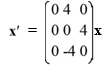
Which of these are eigenvalues for this system? Select all that apply.
A) 0
B) -16
C) 4i
D) -4i
E) -4
F) 4
G) 16

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
61
Consider the first-order homogeneous system of linear differential equations
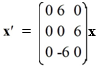
Select the vectors from this list that, together, constitute a fundamental set of solutions for this system.
A)
B)
C)
D)
E)
F)
G)
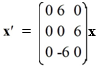
Select the vectors from this list that, together, constitute a fundamental set of solutions for this system.
A)
B)
C)
D)
E)
F)
G)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
62
Consider the first-order homogeneous system of linear differential equations
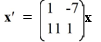
Determine the eigenvalues for this system and describe the behavior of the solution trajectories as t .
A) ; all solution trajectories spiral toward the origin as .
B) ; all solution trajectories spiral away from the origin as .
C) the origin is a saddle.
D) ; all solution trajectories spiral toward the origin as .
E) ; all solution trajectories spiral away from the origin as .
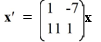
Determine the eigenvalues for this system and describe the behavior of the solution trajectories as t .
A) ; all solution trajectories spiral toward the origin as .
B) ; all solution trajectories spiral away from the origin as .
C) the origin is a saddle.
D) ; all solution trajectories spiral toward the origin as .
E) ; all solution trajectories spiral away from the origin as .

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
63
Consider the first-order homogeneous system of linear differential equations
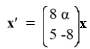
(i) For what real values of α does this system have complex eigenvalues?
(ii) What do the solution trajectories look like for the values of α found in part (i)?
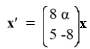
(i) For what real values of α does this system have complex eigenvalues?
(ii) What do the solution trajectories look like for the values of α found in part (i)?

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
64
Consider the first-order homogeneous system of linear differential equations
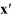 =
= 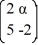 x
x
What is the bifurcation value of α, if any?
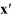 =
= 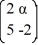 x
xWhat is the bifurcation value of α, if any?

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
65
Consider the first-order homogeneous system of linear differential equations
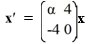
Which of these statements is true?
A) For any real number , the eigenvalues for this system are real numbers.
B) For -8 < < 0, the trajectories spiral towards the origin as t .
C) For < -8, the trajectories spiral away from the origin as t .
D) For = 8, the eigenvalues are purely imaginary and the trajectories are concentric circles centered at the origin.
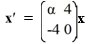
Which of these statements is true?
A) For any real number , the eigenvalues for this system are real numbers.
B) For -8 < < 0, the trajectories spiral towards the origin as t .
C) For < -8, the trajectories spiral away from the origin as t .
D) For = 8, the eigenvalues are purely imaginary and the trajectories are concentric circles centered at the origin.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
66
Consider the first-order homogeneous system of linear differential equations
![<strong>Consider the first-order homogeneous system of linear differential equations The eigenvalues and corresponding eigenvectors for this system are: Which of these is the general solution for this system?</strong> A) \mathbf{x}(t)=C_{1} e^{t}\left[\begin{array}{l}\sin (5 t) \\ -\cos (5 t)\end{array}\right)+C_{2} e^{t}\left[\begin{array}{l}-\sin (5 t) \\ \cos (5 t)\end{array}\right) B) \mathbf{x}(t)=C_{1} e^{t}\left(\begin{array}{l}\sin (5 t) \\ \cos (5 t)\end{array}\right)+C_{2} e^{t}\left(\begin{array}{l}-\sin (5 t) \\ \cos (5 t)\end{array}\right) C) \mathbf{x}(t)=C_{1} e^{t}\left[\begin{array}{l}-\sin (5 t) \\ \cos (5 t)\end{array}\right]+C_{2} e^{t}\left[\begin{array}{l}\cos (5 t) \\ -\sin (5 t)\end{array}\right) D) \mathbf{x}(t)=C_{1} e^{t}\left\{\begin{array}{l}\sin (5 t) \\ \cos (5 t)\end{array}\right]+C_{2} e^{t}\left[\begin{array}{l}\cos (5 t) \\ -\sin (5 t)\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_7040_50f6_9020_95c00c27ee89_TBW1042_11.jpg)
The eigenvalues and corresponding eigenvectors for this system are:
![<strong>Consider the first-order homogeneous system of linear differential equations The eigenvalues and corresponding eigenvectors for this system are: Which of these is the general solution for this system?</strong> A) \mathbf{x}(t)=C_{1} e^{t}\left[\begin{array}{l}\sin (5 t) \\ -\cos (5 t)\end{array}\right)+C_{2} e^{t}\left[\begin{array}{l}-\sin (5 t) \\ \cos (5 t)\end{array}\right) B) \mathbf{x}(t)=C_{1} e^{t}\left(\begin{array}{l}\sin (5 t) \\ \cos (5 t)\end{array}\right)+C_{2} e^{t}\left(\begin{array}{l}-\sin (5 t) \\ \cos (5 t)\end{array}\right) C) \mathbf{x}(t)=C_{1} e^{t}\left[\begin{array}{l}-\sin (5 t) \\ \cos (5 t)\end{array}\right]+C_{2} e^{t}\left[\begin{array}{l}\cos (5 t) \\ -\sin (5 t)\end{array}\right) D) \mathbf{x}(t)=C_{1} e^{t}\left\{\begin{array}{l}\sin (5 t) \\ \cos (5 t)\end{array}\right]+C_{2} e^{t}\left[\begin{array}{l}\cos (5 t) \\ -\sin (5 t)\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_7040_50f7_9020_2320c8fe410e_TBW1042_11.jpg)
Which of these is the general solution for this system?
A)
B)
C)
D)
![<strong>Consider the first-order homogeneous system of linear differential equations The eigenvalues and corresponding eigenvectors for this system are: Which of these is the general solution for this system?</strong> A) \mathbf{x}(t)=C_{1} e^{t}\left[\begin{array}{l}\sin (5 t) \\ -\cos (5 t)\end{array}\right)+C_{2} e^{t}\left[\begin{array}{l}-\sin (5 t) \\ \cos (5 t)\end{array}\right) B) \mathbf{x}(t)=C_{1} e^{t}\left(\begin{array}{l}\sin (5 t) \\ \cos (5 t)\end{array}\right)+C_{2} e^{t}\left(\begin{array}{l}-\sin (5 t) \\ \cos (5 t)\end{array}\right) C) \mathbf{x}(t)=C_{1} e^{t}\left[\begin{array}{l}-\sin (5 t) \\ \cos (5 t)\end{array}\right]+C_{2} e^{t}\left[\begin{array}{l}\cos (5 t) \\ -\sin (5 t)\end{array}\right) D) \mathbf{x}(t)=C_{1} e^{t}\left\{\begin{array}{l}\sin (5 t) \\ \cos (5 t)\end{array}\right]+C_{2} e^{t}\left[\begin{array}{l}\cos (5 t) \\ -\sin (5 t)\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_7040_50f6_9020_95c00c27ee89_TBW1042_11.jpg)
The eigenvalues and corresponding eigenvectors for this system are:
![<strong>Consider the first-order homogeneous system of linear differential equations The eigenvalues and corresponding eigenvectors for this system are: Which of these is the general solution for this system?</strong> A) \mathbf{x}(t)=C_{1} e^{t}\left[\begin{array}{l}\sin (5 t) \\ -\cos (5 t)\end{array}\right)+C_{2} e^{t}\left[\begin{array}{l}-\sin (5 t) \\ \cos (5 t)\end{array}\right) B) \mathbf{x}(t)=C_{1} e^{t}\left(\begin{array}{l}\sin (5 t) \\ \cos (5 t)\end{array}\right)+C_{2} e^{t}\left(\begin{array}{l}-\sin (5 t) \\ \cos (5 t)\end{array}\right) C) \mathbf{x}(t)=C_{1} e^{t}\left[\begin{array}{l}-\sin (5 t) \\ \cos (5 t)\end{array}\right]+C_{2} e^{t}\left[\begin{array}{l}\cos (5 t) \\ -\sin (5 t)\end{array}\right) D) \mathbf{x}(t)=C_{1} e^{t}\left\{\begin{array}{l}\sin (5 t) \\ \cos (5 t)\end{array}\right]+C_{2} e^{t}\left[\begin{array}{l}\cos (5 t) \\ -\sin (5 t)\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_7040_50f7_9020_2320c8fe410e_TBW1042_11.jpg)
Which of these is the general solution for this system?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
67
Consider the first-order homogeneous system of linear differential equations
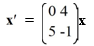
Which of these is the fundamental matrix ?(t) for this system?
A)
B)
C)
D)
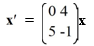
Which of these is the fundamental matrix ?(t) for this system?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
68
Consider the first-order homogeneous system of linear differential equations
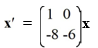
Which of these is the fundamental matrix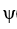 (t) for this system?
(t) for this system?
A)
B)
C)
D)
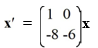
Which of these is the fundamental matrix
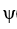 (t) for this system?
(t) for this system?A)
B)
C)
D)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
69
Consider the first-order homogeneous system of linear differential equations
?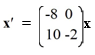
Given a fundamental matrix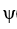 (t) for the system, for what constant vector
(t) for the system, for what constant vector 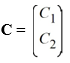 does
does
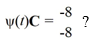
?
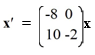
Given a fundamental matrix
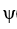 (t) for the system, for what constant vector
(t) for the system, for what constant vector 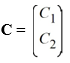 does
does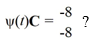

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
70
Consider the first-order homogeneous system of linear differential equations
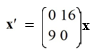
Which of these is the fundamental matrix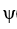 (t) for this system?
(t) for this system?
A)
B)
C)
D)
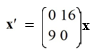
Which of these is the fundamental matrix
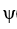 (t) for this system?
(t) for this system?A)
B)
C)
D)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
71
Consider the first-order homogeneous system of linear differential equations
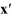 =
= 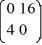 x
x
The columns of the fundamental matrix of this system,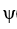 (t), must be linearly independent.
(t), must be linearly independent.
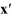 =
= 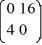 x
xThe columns of the fundamental matrix of this system,
 (t), must be linearly independent.
(t), must be linearly independent.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
72
Consider the first-order homogeneous system of linear differential equations
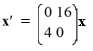
The fundamental matrix of this system,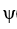 (t), is invertible.
(t), is invertible.
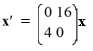
The fundamental matrix of this system,
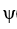 (t), is invertible.
(t), is invertible.
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
73
Consider the first-order homogeneous system of linear differential equations
![<strong>Consider the first-order homogeneous system of linear differential equations Which of these is the fundamental matrix (t) for this system?</strong> A) \psi(t)=\left(\begin{array}{ll}-\sin (3 t) & \cos (3 t) \\ \cos (3 t) & -\sin (3 t)\end{array}\right) B) \Psi(t)=\left(\begin{array}{ll}\sin (3 t) & -\cos (3 t) \\ -\cos (3 t) & \sin (3 t)\end{array}\right) C) \psi(t)=\left(\begin{array}{ll}\sin (3 t) & \cos (3 t) \\ \cos (3 t) & \sin (3 t)\end{array}\right) D) \psi(t)=\left(\begin{array}{ll}\sin (3 t) & -\cos (3 t) \\ \cos (3 t) & \sin (3 t)\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_7040_7816_9020_f7591d66727b_TBW1042_11.jpg)
Which of these is the fundamental matrix![<strong>Consider the first-order homogeneous system of linear differential equations Which of these is the fundamental matrix (t) for this system?</strong> A) \psi(t)=\left(\begin{array}{ll}-\sin (3 t) & \cos (3 t) \\ \cos (3 t) & -\sin (3 t)\end{array}\right) B) \Psi(t)=\left(\begin{array}{ll}\sin (3 t) & -\cos (3 t) \\ -\cos (3 t) & \sin (3 t)\end{array}\right) C) \psi(t)=\left(\begin{array}{ll}\sin (3 t) & \cos (3 t) \\ \cos (3 t) & \sin (3 t)\end{array}\right) D) \psi(t)=\left(\begin{array}{ll}\sin (3 t) & -\cos (3 t) \\ \cos (3 t) & \sin (3 t)\end{array}\right]](https://storage.examlex.com/TBW1042/11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11.jpg) (t) for this system?
(t) for this system?
A)
B)
C)
D)
![<strong>Consider the first-order homogeneous system of linear differential equations Which of these is the fundamental matrix (t) for this system?</strong> A) \psi(t)=\left(\begin{array}{ll}-\sin (3 t) & \cos (3 t) \\ \cos (3 t) & -\sin (3 t)\end{array}\right) B) \Psi(t)=\left(\begin{array}{ll}\sin (3 t) & -\cos (3 t) \\ -\cos (3 t) & \sin (3 t)\end{array}\right) C) \psi(t)=\left(\begin{array}{ll}\sin (3 t) & \cos (3 t) \\ \cos (3 t) & \sin (3 t)\end{array}\right) D) \psi(t)=\left(\begin{array}{ll}\sin (3 t) & -\cos (3 t) \\ \cos (3 t) & \sin (3 t)\end{array}\right]](https://storage.examlex.com/TBW1042/11eeb833_7040_7816_9020_f7591d66727b_TBW1042_11.jpg)
Which of these is the fundamental matrix
![<strong>Consider the first-order homogeneous system of linear differential equations Which of these is the fundamental matrix (t) for this system?</strong> A) \psi(t)=\left(\begin{array}{ll}-\sin (3 t) & \cos (3 t) \\ \cos (3 t) & -\sin (3 t)\end{array}\right) B) \Psi(t)=\left(\begin{array}{ll}\sin (3 t) & -\cos (3 t) \\ -\cos (3 t) & \sin (3 t)\end{array}\right) C) \psi(t)=\left(\begin{array}{ll}\sin (3 t) & \cos (3 t) \\ \cos (3 t) & \sin (3 t)\end{array}\right) D) \psi(t)=\left(\begin{array}{ll}\sin (3 t) & -\cos (3 t) \\ \cos (3 t) & \sin (3 t)\end{array}\right]](https://storage.examlex.com/TBW1042/11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11.jpg) (t) for this system?
(t) for this system?A)
B)
C)
D)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
74
Consider the first-order homogeneous system of linear differential equations
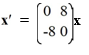
Given a fundamental matrix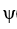 (t) for the system, which of these is the general solution of this system?
(t) for the system, which of these is the general solution of this system?
Here,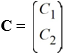 is an arbitrary constant vector.
is an arbitrary constant vector.
A)
B)
C)
D)
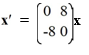
Given a fundamental matrix
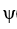 (t) for the system, which of these is the general solution of this system?
(t) for the system, which of these is the general solution of this system?Here,
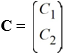 is an arbitrary constant vector.
is an arbitrary constant vector.A)
B)
C)
D)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
75
Consider the first-order homogeneous system of linear differential equations
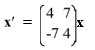
Which of these is the fundamental matrix (t) for this system?
(t) for this system?
A)
B)
C)
D)
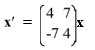
Which of these is the fundamental matrix
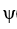 (t) for this system?
(t) for this system?A)
B)
C)
D)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
76
Consider the first-order homogeneous system of linear differential equations
X = x
x
Given a fundamental matrix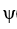 (t) for the system, which of these is the general solution of this system? Here, C =
(t) for the system, which of these is the general solution of this system? Here, C = 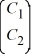 is an arbitrary constant vector.
is an arbitrary constant vector.
A) x(t) = 11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11 (t)C
B) x(t) = 11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11 (t) + C
C) x(t) = 11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11 -1(t)C
D) x(t) = 11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11 (0)C
X =
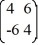 x
xGiven a fundamental matrix
 (t) for the system, which of these is the general solution of this system? Here, C =
(t) for the system, which of these is the general solution of this system? Here, C = 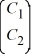 is an arbitrary constant vector.
is an arbitrary constant vector.A) x(t) = 11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11 (t)C
B) x(t) = 11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11 (t) + C
C) x(t) = 11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11 -1(t)C
D) x(t) = 11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11 (0)C

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
77
Consider the first-order homogeneous system of linear differential equations
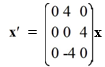
Which of these is the fundamental matrix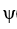 (t) for this system?
(t) for this system?
A)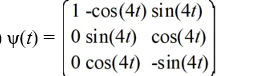
B)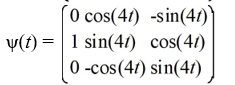
C)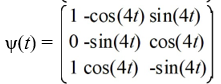
D)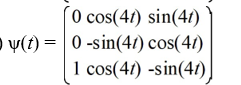
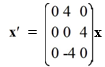
Which of these is the fundamental matrix
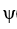 (t) for this system?
(t) for this system?A)
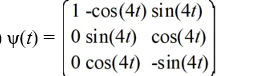
B)
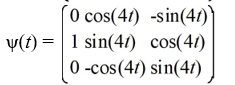
C)
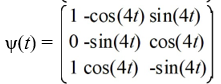
D)
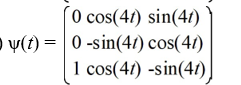

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
78
Consider the first-order homogeneous system of linear differential equations
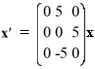
Given a fundamental matrix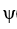 (t) for the system, which of these is the general solution of this system? Here,
(t) for the system, which of these is the general solution of this system? Here, 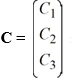 is an arbitrary constant vector.
is an arbitrary constant vector.
A) x(t) = 11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11 (t)C
B) x(t) = 11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11 (t) + C
C) x(t) = 11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11 -1(t)C
D) x(t) = 11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11 (0)C
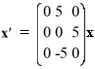
Given a fundamental matrix
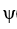 (t) for the system, which of these is the general solution of this system? Here,
(t) for the system, which of these is the general solution of this system? Here, 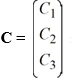 is an arbitrary constant vector.
is an arbitrary constant vector.A) x(t) = 11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11 (t)C
B) x(t) = 11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11 (t) + C
C) x(t) = 11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11 -1(t)C
D) x(t) = 11eec32a_dc1b_6687_8720_5fa3d39c7544_TBW1042_11 (0)C

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
79
Consider the first-order homogeneous system of linear differential equations
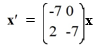
Select a pair of vectors from these choices that constitute a fundamental set of solutions for this system.
A)
B)
C)
D)
E)
F)
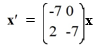
Select a pair of vectors from these choices that constitute a fundamental set of solutions for this system.
A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
80
Consider the first-order homogeneous system of linear differential equations
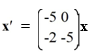
What is the general solution of this system?
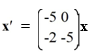
What is the general solution of this system?

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck


