Deck 6: The Laplace Transform
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/57
Play
Full screen (f)
Deck 6: The Laplace Transform
1
Consider the following function:
F(t) =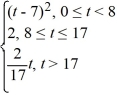
Which of these properties does f satisfy? Select all that apply.
A) f is piecewise continuous on [0, ).
B) f is of exponential order.
C) f is continuous on [0, ).
D)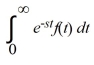 diverges.
diverges.
E) The Laplace transform of f exists.
F(t) =
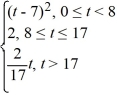
Which of these properties does f satisfy? Select all that apply.
A) f is piecewise continuous on [0, ).
B) f is of exponential order.
C) f is continuous on [0, ).
D)
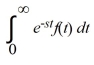 diverges.
diverges.E) The Laplace transform of f exists.
f is piecewise continuous on [0, ).
f is of exponential order.
The Laplace transform of f exists.
f is of exponential order.
The Laplace transform of f exists.
2
Consider the following function:
F(t) =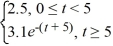
Which of the following statements is true?
A) The Laplace transform of f does not exist because f is not of exponential order.
B)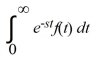 converges.
converges.
C) f is continuous on [0, )
D) f is piecewise continuous on [0, ), but the Laplace transform of f does not exist.
F(t) =
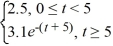
Which of the following statements is true?
A) The Laplace transform of f does not exist because f is not of exponential order.
B)
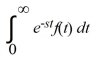 converges.
converges.C) f is continuous on [0, )
D) f is piecewise continuous on [0, ), but the Laplace transform of f does not exist.
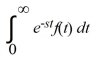 converges.
converges. 3
Compute the Laplace transform of f:
F(t) =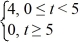
A)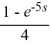 , s > 0
, s > 0
B)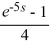 , s > 0
, s > 0
C)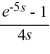 , s > 0
, s > 0
D)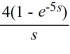 , s > 0
, s > 0
F(t) =
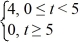
A)
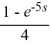 , s > 0
, s > 0B)
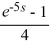 , s > 0
, s > 0C)
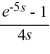 , s > 0
, s > 0D)
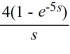 , s > 0
, s > 0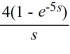 , s > 0
, s > 0 4
Compute the Laplace transform of f:
F(t) =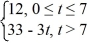
A)
B)
C)
D)
F(t) =
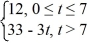
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
5
The integral 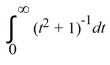 converges.
converges.
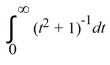 converges.
converges.
Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
6
Which of these statements is true?
A) converges because , for all and converges.
B) diverges because , for all and converges.
C) converges because is of exponential order.
D) converges because is of exponential order.
A) converges because , for all and converges.
B) diverges because , for all and converges.
C) converges because is of exponential order.
D) converges because is of exponential order.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
7
Compute the Laplace transform of f(t) = 4.2.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
8
Compute the Laplace transform of f(t) = 6t - 5 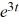 .
.
A) +
+ 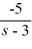 , s > 3
, s > 3
B)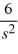 +
+ 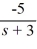 , s > -3
, s > -3
C)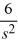 +
+ 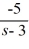 , s > 3
, s > 3
D) +
+ 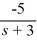 , s > -3
, s > -3
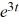 .
.A)
 +
+ 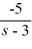 , s > 3
, s > 3B)
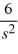 +
+ 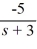 , s > -3
, s > -3C)
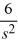 +
+ 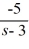 , s > 3
, s > 3D)
 +
+ 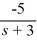 , s > -3
, s > -3
Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
9
Compute the Laplace transform of f(t) = 3 sin(6t) - 4 cos(6t).
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
10
Compute the Laplace transform of f(t) = t cos(10t).
A)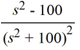
B)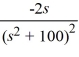
C)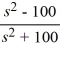
D)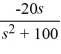
E)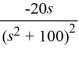
A)
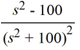
B)
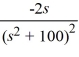
C)
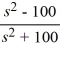
D)
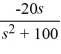
E)
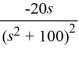

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
11
Compute the Laplace transform of f(t) = sin(2 t)cos(2 t).
A)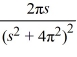
B)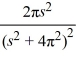
C)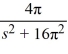
D)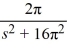
A)
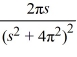
B)
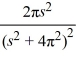
C)
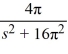
D)
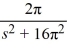

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
12
Compute the Laplace transform of f(t) = 3 + 10 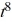 .
.
A)
B)
C)
D)
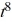 .
.A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
13
Compute the inverse Laplace transform of F(s) = 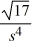 +
+ 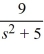 .
.
A)
B)
C)
D)
E)
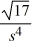 +
+ 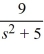 .
.A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
14
Compute the inverse Laplace transform of 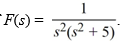
A)
B)
C)
D)
E)
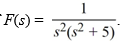
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
15
Compute the inverse Laplace transform of F(s) = 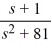 .
.
A)
B)
C)
D)
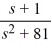 .
.A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
16
Compute the inverse Laplace transform of 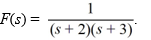
A)
B)
C)
D)
E)
F)
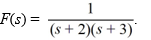
A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
17
Find the Laplace transform of the solution x(t) of the following initial value problem: 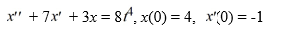
A)
B)
C)
D)
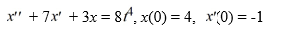
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
18
Find the Laplace transform of the solution x(t) of the following initial value problem: 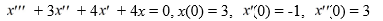
A)
B)
C)
D)
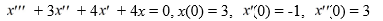
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
19
Consider the following initial value problem:
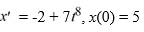
(ii) Find the inverse Laplace transform of the answer in part (i) to find the solution x(t) of the initial value problem.
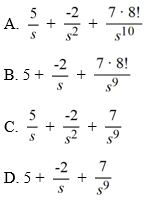
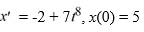
(ii) Find the inverse Laplace transform of the answer in part (i) to find the solution x(t) of the initial value problem.
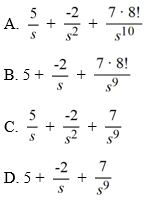

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
20
Find the Laplace transform of the solution x(t) of the following initial value problem:
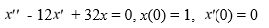
A)
B)
C)
D)
E)
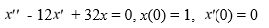
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
21
Compute the Laplace transform of f(t) = 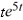 sin(5t).
sin(5t).
A)
B)
C)
D)
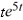 sin(5t).
sin(5t).A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
22
Compute the Laplace transform of 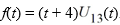
A)
B)
C)
D)
E)
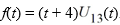
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
23
Compute the Laplace transform of 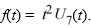
A)
B)
C)
D)
E)
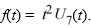
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
24
Consider the function
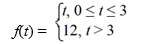
Express f(t) using unit step functions.
A)
B)
C)
D)
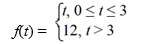
Express f(t) using unit step functions.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
25
Consider the function
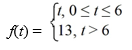
Compute the Laplace transform of f(t).
A)
B)
C)
D)
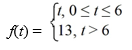
Compute the Laplace transform of f(t).
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
26
Consider the function
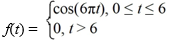
Express f(t) using unit step functions.
A)
B)
C)
D)
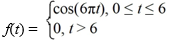
Express f(t) using unit step functions.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the function
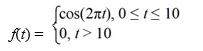
Compute the Laplace transform of f(t).
A)
B)
C)
D)
E)
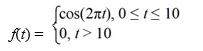
Compute the Laplace transform of f(t).
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
28
Consider the function

Express f(t) using unit step functions.
A)
B)
C)
D)

Express f(t) using unit step functions.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
29
Consider the function
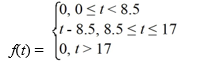
Compute the Laplace transform of f(t).
A)
B)
C)
D)
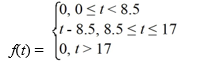
Compute the Laplace transform of f(t).
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
30
Compute the inverse Laplace transform of F(s) = ![<strong>Compute the inverse Laplace transform of F(s) = .</strong> A) e^{-2 t}\left[\cos (\sqrt{11} t)+\frac{4}{\sqrt{11}} \sin (\sqrt{11} t)\right] B) e^{2 t}\left(\cos (\sqrt{11} t)+\frac{4}{\sqrt{11}} \sin (\sqrt{11} t)\right) C) e^{2 t}\left(\frac{4}{\sqrt{11}} \cos (\sqrt{11} t)+\sin (\sqrt{11} t)\right) D) e^{-2 t}\left(\frac{4}{\sqrt{11}} \cos (\sqrt{11} t)+\sin (\sqrt{11} t)\right)](https://storage.examlex.com/TBW1042/11eeb833_7042_2542_9020_f94392e64f68_TBW1042_11.jpg) .
.
A)
B)
C)
D)
![<strong>Compute the inverse Laplace transform of F(s) = .</strong> A) e^{-2 t}\left[\cos (\sqrt{11} t)+\frac{4}{\sqrt{11}} \sin (\sqrt{11} t)\right] B) e^{2 t}\left(\cos (\sqrt{11} t)+\frac{4}{\sqrt{11}} \sin (\sqrt{11} t)\right) C) e^{2 t}\left(\frac{4}{\sqrt{11}} \cos (\sqrt{11} t)+\sin (\sqrt{11} t)\right) D) e^{-2 t}\left(\frac{4}{\sqrt{11}} \cos (\sqrt{11} t)+\sin (\sqrt{11} t)\right)](https://storage.examlex.com/TBW1042/11eeb833_7042_2542_9020_f94392e64f68_TBW1042_11.jpg) .
.A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
31
Consider the function
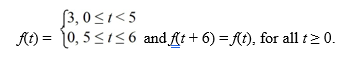
Compute the Laplace transform of f(t).
A)
B)
C)
D)
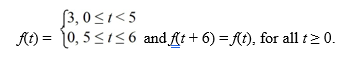
Compute the Laplace transform of f(t).
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
32
Compute the inverse Laplace transform of 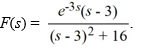
A)
B)
C)
D)
E)
F)
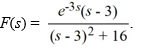
A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
33
Compute the Laplace transform of 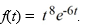
A)
B)
C)
D)
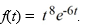
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
34
Compute the Laplace transform of 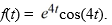
A)
B)
C)
D)
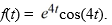
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
35
Compute the inverse Laplace transform of 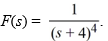 .
.
A)
B)
C)
D)
E)
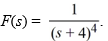 .
.A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
36
Consider the function
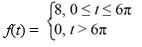
Express f(t) using unit step functions.
A)
B)
C)
D)
E)
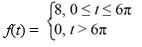
Express f(t) using unit step functions.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
37
Compute the inverse Laplace transform of 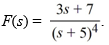
A)
B)
C)
D)
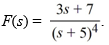
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
38
Find the Laplace transform of the solution x(t) of the following initial value problem:
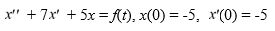
Wher
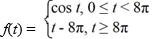
A)
B)
C)
D)
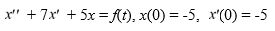
Wher
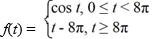
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
39
Find the Laplace transform of the solution x(t) of the following initial value problem
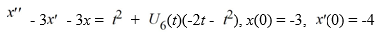
A)
B)
C)
D)
E)
F)
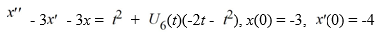
A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
40
Find the Laplace transform of the solution x(t) of the following initial value problem
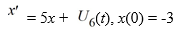
A)
B)
C)
D)
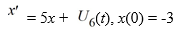
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
41
Find the Laplace transform of the solution x(t) of the following initial value problem
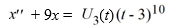
A)
B)
C)
D)
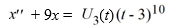
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
42
You are given a spring-mass system with a mass of 1 slug, a damping constant 8 lb-sec/foot, and a spring constant of 16 lbs/foot. Suppose the mass is released from rest 1.5 feet below equilibrium, and after 5π seconds the system is given a sharp blow downward which imparts a unit impulse.
(i) Write down a second-order initial value problem whose solution x(t) is the equation of motion for this system.
(ii) Find the Laplace transform X(s) of the solution x(t) of the initial value problem you formulated in part (i).
(iii) Compute the inverse Laplace transform of your function in part (ii).
(i) Write down a second-order initial value problem whose solution x(t) is the equation of motion for this system.
(ii) Find the Laplace transform X(s) of the solution x(t) of the initial value problem you formulated in part (i).
(iii) Compute the inverse Laplace transform of your function in part (ii).

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
43
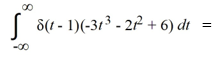 ________. Here, δ stands for the Dirac delta function.
________. Here, δ stands for the Dirac delta function.
Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
44
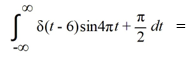 ________. Here, δ stands for the Dirac delta function.
________. Here, δ stands for the Dirac delta function.
Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
45
Compute the Laplace transform of f(t) = δ(t + 3), where δ stands for the Dirac delta function.

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
46
Find the Laplace transform of the solution of x(t) of the following initial value problem
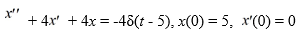
A)
B)
C)
D)
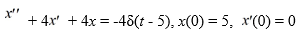
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
47
Consider the following initial value problem
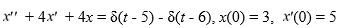
(i) Find the Laplace transform X(s) of the solution x(t) of this initial value problem.
(ii) Compute the inverse Laplace transform of your function in part (i).
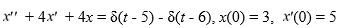
(i) Find the Laplace transform X(s) of the solution x(t) of this initial value problem.
(ii) Compute the inverse Laplace transform of your function in part (i).

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
48
Compute 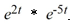
A)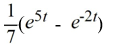
B)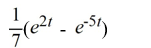
C)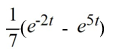
D)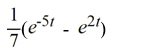
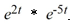
A)
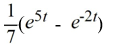
B)
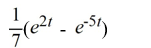
C)
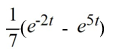
D)
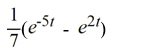

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
49
Which of the following are properties of the convolution integral, for all continuous functions f, g, and h? Select all that apply.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
50
Compute the Laplace transform of f(t) = 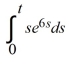 .
.
A)
B)
C)
D)
E)
F)
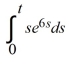 .
.A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
51
Consider the following initial value problem describing the motion of a harmonic oscillator in the absence of friction, but subject to an external force.
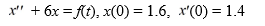
Find the Laplace transform X(s) of the solution x(t) of this initial value problem. Here, F(s) stands for the Laplace transform of f(t).
A)
B)
C)
D)
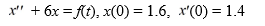
Find the Laplace transform X(s) of the solution x(t) of this initial value problem. Here, F(s) stands for the Laplace transform of f(t).
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
52
Consider the following initial value problem describing the motion of a harmonic oscillator in the absence of friction, but subject to an external force.
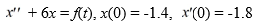
Find the equation of motion x(t). (Hint: You will need to use a convolution integral.)
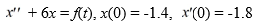
Find the equation of motion x(t). (Hint: You will need to use a convolution integral.)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
53
Find the function f(t) that satisfies the integral equationf(t)
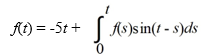
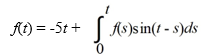

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
54
Compute 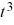 * t.
* t.
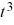 * t.
* t.
Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
55
Use the convolution theorem to compute the inverse Laplace transform of 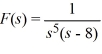
A)
B)
C)
D)
E)
F)
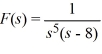
A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
56
Find the function f(t) that satisfies the integral equationf(t)
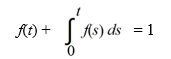
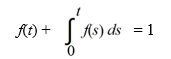

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck
57
Use the convolution theorem to compute the inverse Laplace transform of
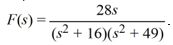 Select all that apply.
Select all that apply.
A) 28 sin(4t) * cos(7t)
B) 7 sin(4t) * cos(7t)
C) 4 sin(4t) * cos(7t)
D) 4 sin(7t) * cos(4t)
E) 7 sin(7t) * cos(4t)
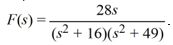 Select all that apply.
Select all that apply.A) 28 sin(4t) * cos(7t)
B) 7 sin(4t) * cos(7t)
C) 4 sin(4t) * cos(7t)
D) 4 sin(7t) * cos(4t)
E) 7 sin(7t) * cos(4t)

Unlock Deck
Unlock for access to all 57 flashcards in this deck.
Unlock Deck
k this deck


