Deck 5: Series Solutions of Second-Order Linear Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/81
Play
Full screen (f)
Deck 5: Series Solutions of Second-Order Linear Equations
1
What is the radius of convergence of the power series 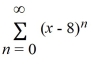 ?
?
A) 0
B) 1
C) 8
D)
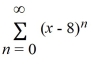 ?
?A) 0
B) 1
C) 8
D)
1
2
What is the radius of convergence of the power series 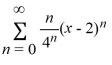 ?
?
A)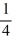
B) 4
C) 2
D) 6
E)
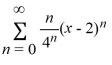 ?
?A)
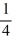
B) 4
C) 2
D) 6
E)
4
3
What is the radius of convergence of the power series 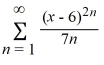 ?
?
A) 0
B)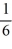
C) 1
D) 6
E) 7
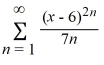 ?
?A) 0
B)
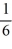
C) 1
D) 6
E) 7
1
4
What is the radius of convergence of the power series 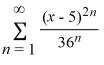 ?
?
A) 5
B) 6
C) 36
D)
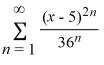 ?
?A) 5
B) 6
C) 36
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
5
What is the Taylor series expansion for f(x) = sin(6x) about x = 0?
A)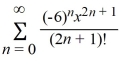
B)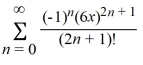
C)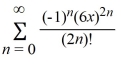
D)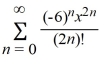
A)
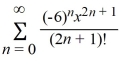
B)
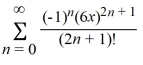
C)
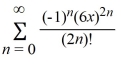
D)
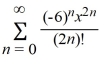

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
6
What is the Taylor expansion for f(x) = cos(7x) about x = 0?
A)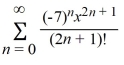
B)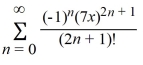
C)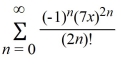
D)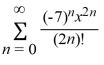
A)
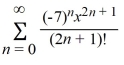
B)
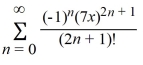
C)
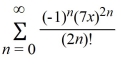
D)
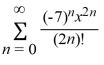

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
7
What is the Taylor series expansion for f(x) = 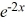 about x = 0?
about x = 0?
A)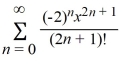
B)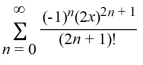
C)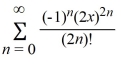
D)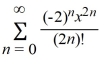
E)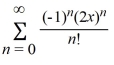
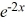 about x = 0?
about x = 0?A)
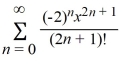
B)
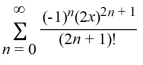
C)
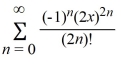
D)
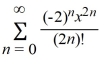
E)
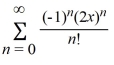

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
8
Which of these power series is equivalent to 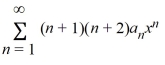 ? Select all that apply.
? Select all that apply.
A)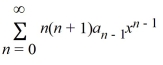
B)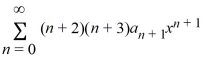
C)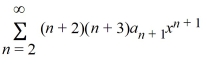
D)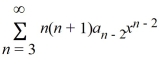
E)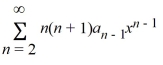
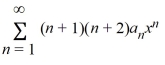 ? Select all that apply.
? Select all that apply.A)
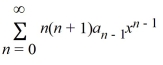
B)
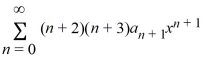
C)
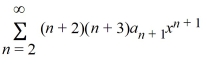
D)
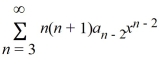
E)
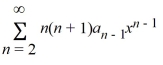

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
9
Which of these power series is equivalent to 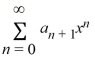 + 7
+ 7 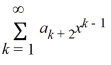 ?
?
A)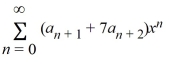
B)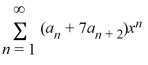
C) ?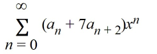
D) ?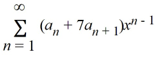
E)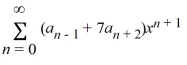
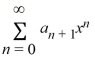 + 7
+ 7 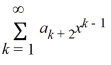 ?
?A)
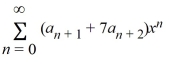
B)
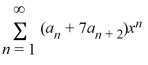
C) ?
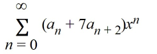
D) ?
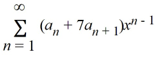
E)
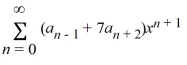

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
10
Which of these are singular points for the differential equation
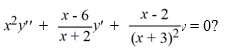
Select all that apply.
A) -2
B) 6
C) -3
D) 2
E) 0
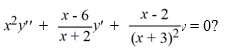
Select all that apply.
A) -2
B) 6
C) -3
D) 2
E) 0

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
11
Which of these are ordinary points for the differential equation
(x + 5)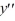 + (
+ ( 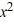 - 49)
- 49) 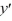 + 2xy = 0?
+ 2xy = 0?
Select all that apply.
A) -5
B) -7
C) 7
D) 0
E) 12
(x + 5)
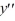 + (
+ ( 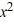 - 49)
- 49) 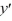 + 2xy = 0?
+ 2xy = 0?Select all that apply.
A) -5
B) -7
C) 7
D) 0
E) 12

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
12
Which of these are singular points for the differential equation
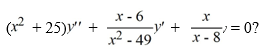
Select all that apply.
A) -5
B) -7
C) 5
D) 6
E) 7
F) 8
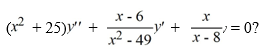
Select all that apply.
A) -5
B) -7
C) 5
D) 6
E) 7
F) 8

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
13
Consider the second-order differential equation 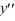 + 64y = 0.
+ 64y = 0.
Assume a solution of this equation can be represented as a power series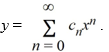
What is the recurrence relation for the coefficientsCn ? Assume that C0 and C1 are known.
A)
B)
C)
D)
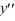 + 64y = 0.
+ 64y = 0.Assume a solution of this equation can be represented as a power series
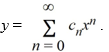
What is the recurrence relation for the coefficientsCn ? Assume that C0 and C1 are known.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
14
Consider the second-order differential equation 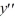 + 49y = 0.
+ 49y = 0.
Assume a solution of this equation can be represented as a power series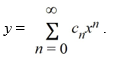
Write down the explicit formulas for the coefficients Cn
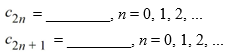
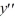 + 49y = 0.
+ 49y = 0.Assume a solution of this equation can be represented as a power series
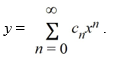
Write down the explicit formulas for the coefficients Cn
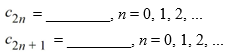

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
15
Consider the second-order differential equation 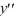 + 100y = 0.
+ 100y = 0.
Assume a solution of this equation can be represented as a power series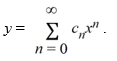
Assume the solution of the given differential equation is written as
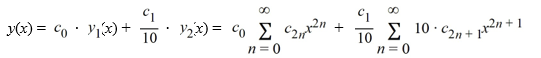
Identify elementary functions for y1 (x) and y2 (x).
y1 (x) = ________
y2 (x) = ________
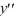 + 100y = 0.
+ 100y = 0.Assume a solution of this equation can be represented as a power series
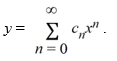
Assume the solution of the given differential equation is written as
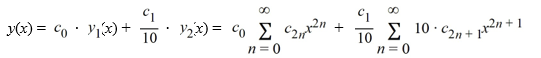
Identify elementary functions for y1 (x) and y2 (x).
y1 (x) = ________
y2 (x) = ________

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
16
Consider the second-order differential equation 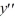 - 4x
- 4x 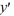 + y = 0.
+ y = 0.
Assume a solution of this equation can be represented as a power series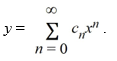
What is the recurrence relation for the coefficients Cn? Assume that C0 and C1 are known
A)
B)
C)
D)
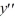 - 4x
- 4x 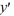 + y = 0.
+ y = 0.Assume a solution of this equation can be represented as a power series
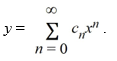
What is the recurrence relation for the coefficients Cn? Assume that C0 and C1 are known
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
17
Consider the second-order differential equation 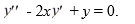
Assume a solution of this equation can be represented as a power series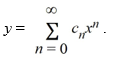
Write down the following explicit formulas for the coefficients Cn:
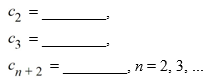
C2n= ________, n = 0, 1, 2, ...
C2n+1= ________, n = 0, 1, 2, ...
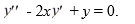
Assume a solution of this equation can be represented as a power series
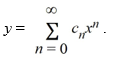
Write down the following explicit formulas for the coefficients Cn:
C2n= ________, n = 0, 1, 2, ...
C2n+1= ________, n = 0, 1, 2, ...

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
18
Consider the first-order differential equation 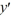 - 5y = 0.
- 5y = 0.
Assume a solution of this equation can be represented as a power series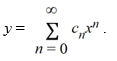
What is the recurrence relation for the coefficients Cn? Assume that C0 is known
A)
B)
C)
D)
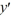 - 5y = 0.
- 5y = 0.Assume a solution of this equation can be represented as a power series
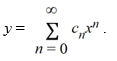
What is the recurrence relation for the coefficients Cn? Assume that C0 is known
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
19
Consider the first-order differential equation 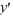 - 7y = 0.
- 7y = 0.
Assume a solution of this equation can be represented as a power series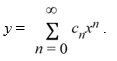
Write down the following explicit formula for the coefficients Cn
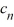 = , n = 0, 1, 2, ...
= , n = 0, 1, 2, ...
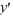 - 7y = 0.
- 7y = 0.Assume a solution of this equation can be represented as a power series
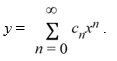
Write down the following explicit formula for the coefficients Cn
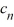 = , n = 0, 1, 2, ...
= , n = 0, 1, 2, ...
Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
20
Consider the first-order differential equation 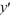 - 7y = 0.
- 7y = 0.
Assume a solution of this equation can be represented as a power series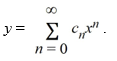
Which of these elementary functions is equal to the power series representation of the solution?
A)
B)
C)
D)
E)
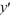 - 7y = 0.
- 7y = 0.Assume a solution of this equation can be represented as a power series
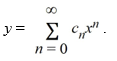
Which of these elementary functions is equal to the power series representation of the solution?
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
21
Consider the first-order differential equation 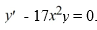
Assume a solution of this equation can be represented as a power series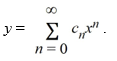 .
.
Assume that C0 is known.
Which of these power series equals y(x)?
A)
B)
C)
D)
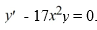
Assume a solution of this equation can be represented as a power series
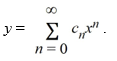 .
.Assume that C0 is known.
Which of these power series equals y(x)?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
22
Consider the first-order differential equation 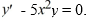
Assume a solution of this equation can be represented as a power series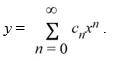
Assume that C0 is known.
Identify an elementary function equal to y(x).
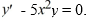
Assume a solution of this equation can be represented as a power series
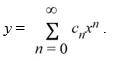
Assume that C0 is known.
Identify an elementary function equal to y(x).

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
23
Consider the first-order differential equation
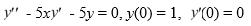 .
.
Assume a solution of this equation can be represented as a power series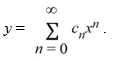 .
.
Write down the following explicit formulas for the coefficients Cn
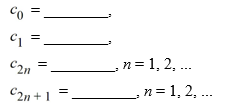 .
.
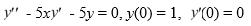 .
. Assume a solution of this equation can be represented as a power series
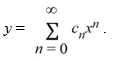 .
. Write down the following explicit formulas for the coefficients Cn
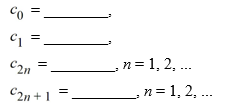 .
.
Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
24
Consider this initial value problem: 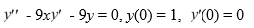 .
.
Assume a solution of this equation can be represented as a power series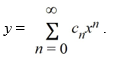 .
.
Express the solution y(x) as an elementary function.
A)
B)
C)
D)
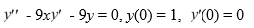 .
.Assume a solution of this equation can be represented as a power series
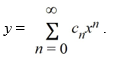 .
.Express the solution y(x) as an elementary function.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
25
Consider the first-order differential equation 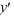 . - 7xy = 0.
. - 7xy = 0.
Assume a solution of this equation can be represented as a power series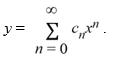 .
.
What is the recurrence relation for the coefficients Cn ? Assume that C0 is known.
A)
B)
C)
D)
E)
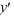 . - 7xy = 0.
. - 7xy = 0.Assume a solution of this equation can be represented as a power series
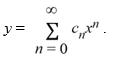 .
.What is the recurrence relation for the coefficients Cn ? Assume that C0 is known.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
26
Consider the first-order differential equation 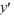 - 10xy = 0.
- 10xy = 0.
Assume a solution of this equation can be represented as a power series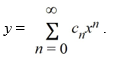
Express the solution y(x) as an elementary function.
A)
B)
C)
D)
E)
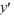 - 10xy = 0.
- 10xy = 0.Assume a solution of this equation can be represented as a power series
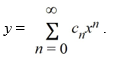
Express the solution y(x) as an elementary function.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the second-order differential equation 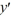 - 1 y = 0.
- 1 y = 0.
Assume a solution of this equation can be represented as a power series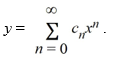
Assume that C0 and C1 are known. Write down the following explicit formulas for the coefficients Cn
 .
.
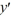 - 1 y = 0.
- 1 y = 0.Assume a solution of this equation can be represented as a power series
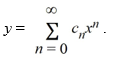
Assume that C0 and C1 are known. Write down the following explicit formulas for the coefficients Cn
 .
.
Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
28
Consider the second-order differential equation 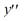 - 19x2 y = 0.
- 19x2 y = 0.
Assume a solution of this equation can be represented as a power series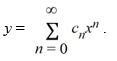
Write down the first four nonzero terms of the power series solution.
y(x) ≈ ________
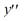 - 19x2 y = 0.
- 19x2 y = 0.Assume a solution of this equation can be represented as a power series
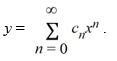
Write down the first four nonzero terms of the power series solution.
y(x) ≈ ________

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
29
Consider this initial-value problem: 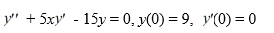 .
.
Assume a solution of this equation can be represented as a power series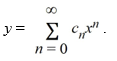 .
.
Write down the values of these coefficients:
C0 = ________,
C1 = ________,
C2 = ________,
C3 = ________,
C4 = ________,
C5 = ________,
C6 = ________
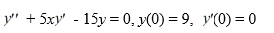 .
. Assume a solution of this equation can be represented as a power series
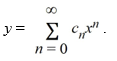 .
. Write down the values of these coefficients:
C0 = ________,
C1 = ________,
C2 = ________,
C3 = ________,
C4 = ________,
C5 = ________,
C6 = ________

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
30
Consider this initial-value problem: 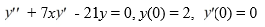 .
.
Assume a solution of this equation can be represented as a power series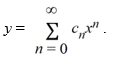 .
.
Write down the first four terms of the power series solution.
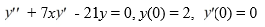 .
. Assume a solution of this equation can be represented as a power series
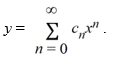 .
. Write down the first four terms of the power series solution.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
31
Consider the second-order differential equation 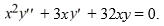 .
.
Assume the solution can be expressed as a power series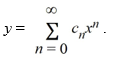 . Assume C0 = 0. Find C1
. Assume C0 = 0. Find C1
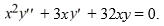 .
. Assume the solution can be expressed as a power series
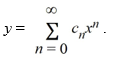 . Assume C0 = 0. Find C1
. Assume C0 = 0. Find C1
Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
32
What is the greatest lower bound for the radius of convergence of a series solution for the second-order differential equation (x + 8) 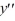 - 7x
- 7x 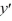 + 7y = 0 about the point
+ 7y = 0 about the point 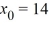 ?
?
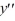 - 7x
- 7x 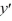 + 7y = 0 about the point
+ 7y = 0 about the point 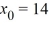 ?
?
Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
33
What is the greatest lower bound for the radius of convergence of a series solution for the second-order differential equation (x - 2)(x + 4) 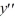 +7(X +16)
+7(X +16) 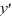 - 8xy = 0 about the point ?
- 8xy = 0 about the point ?
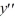 +7(X +16)
+7(X +16) 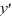 - 8xy = 0 about the point ?
- 8xy = 0 about the point ?
Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
34
What is a lower bound for the radius of convergence of a series solution for the second-order differential equation (x - 2)(x + 4) 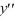 + 8(x + 7)
+ 8(x + 7) 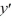 - 7xy = 0 about the point
- 7xy = 0 about the point 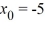 ?
?
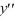 + 8(x + 7)
+ 8(x + 7) 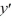 - 7xy = 0 about the point
- 7xy = 0 about the point 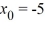 ?
?
Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
35
What is a lower bound for the radius of convergence of a series solution for the second-order differential equation (x - 6)(x + 12) 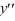 + 6(x + 14)
+ 6(x + 14) 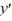 - 2xy = 0 about the point X0 = 11?
- 2xy = 0 about the point X0 = 11?
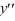 + 6(x + 14)
+ 6(x + 14) 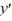 - 2xy = 0 about the point X0 = 11?
- 2xy = 0 about the point X0 = 11?
Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
36
What is the radius of convergence of a series solution for the second-order differential equation 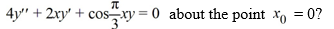 .
.
A) 0
B) 1
C)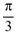 .
.
D)
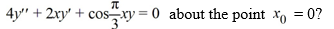 .
.A) 0
B) 1
C)
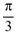 .
.D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
37
What is a lower bound for the radius of convergence of a series solution for the second-order differential equation 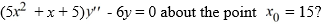 .
.
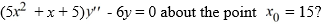 .
.
Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
38
What is the greatest lower bound of the radius of convergence of a series solution for the second-order differential equation 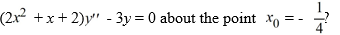 .
.
A)
B)
C)
D)
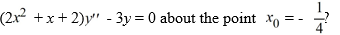 .
.A)
B)
C)
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
39
Which of the following pairs forms a fundamental set of solutions of the Cauchy Euler differential equation 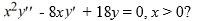 .
.
A)
B)
C)
D)
E)
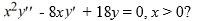 .
.A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
40
Which of the following pairs forms a fundamental set of solutions of the Cauchy Euler differential equation 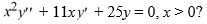 .
.
A)
B)
C)
D)
E)
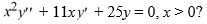 .
.A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
41
Which of the following pairs forms a fundamental set of solutions of the Cauchy Euler differential equation 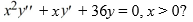 .
.
A)
B)
C)
D)
E)
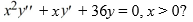 .
.A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
42
Find the general solution of the Cauchy Euler differential equation 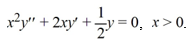 .
.
A)
B)
C)
D)
E)
F)
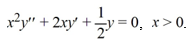 .
.A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
43
Find the general solution of the Cauchy Euler differential equation 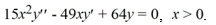 .
.
A)
B)
C)
D)
E)
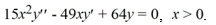 .
.A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
44
Find the general solution of the Cauchy Euler differential equation 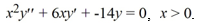 .
.
A)
B)
C)
D)
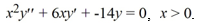 .
.A)
B)
C)
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
45
Solve this initial value problem: 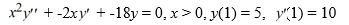 .
.
A)
B)
C)
D)
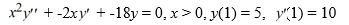 .
.A)
B)
C)
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
46
Solve this initial value problem: 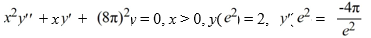 .
.
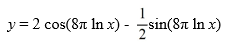 .
.
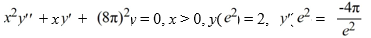 .
. 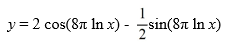 .
.
Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
47
Find the general solution of the Cauchy Euler differential equation 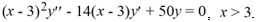 .
.
A)
B)
C)
D)
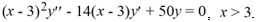 .
.A)
B)
C)
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
48
Find the general solution of the Cauchy Euler differential equation 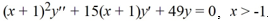 .
.
A)
B)
C)
D)
E)
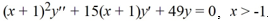 .
.A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
49
Consider the Bessel equation of order 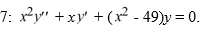 .
.
Which of these statements is true?
A) x = 7 is a regular singular point.
B) x = 0 is a regular singular point.
C) x = 0 is an irregular singular point.
D) There are no singular points.
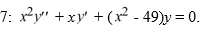 .
.Which of these statements is true?
A) x = 7 is a regular singular point.
B) x = 0 is a regular singular point.
C) x = 0 is an irregular singular point.
D) There are no singular points.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
50
Consider the Legendre equation: 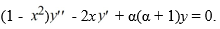 .
.
Which of these statements is true?
A) x = 1 is a regular singular point and x = -1 is an irregular singular point.
B) x = 1 is an irregular singular point and x = -1 is a regular singular point.
C) Both x = 1 and x = -1 are regular singular points.
D) Both x = 1 and x = -1 are irregular singular points.
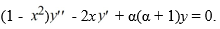 .
.Which of these statements is true?
A) x = 1 is a regular singular point and x = -1 is an irregular singular point.
B) x = 1 is an irregular singular point and x = -1 is a regular singular point.
C) Both x = 1 and x = -1 are regular singular points.
D) Both x = 1 and x = -1 are irregular singular points.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
51
Consider the second-order differential equation 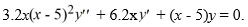 .
.
Which of these statements is true?
A) x = 0 is a regular singular point and x = 5 is an irregular singular point.
B) x = 0 is an irregular singular point and x = 5 is a regular singular point.
C) Both x = 0 and x = 5 are regular singular points.
D) Both x = 0 and x = 5 are irregular singular points.
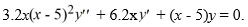 .
.Which of these statements is true?
A) x = 0 is a regular singular point and x = 5 is an irregular singular point.
B) x = 0 is an irregular singular point and x = 5 is a regular singular point.
C) Both x = 0 and x = 5 are regular singular points.
D) Both x = 0 and x = 5 are irregular singular points.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
52
Consider the second-order differential equation: 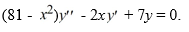 .
.
Which of these statements is true?
A) x = 9 and x = -9 are both regular singular points.
B) x = 9 and x = -9 are both irregular singular points.
C) x = 0 and x = 9 are regular singular points, and x = -9 is an irregular singular point.
D) x = 0 and x = -9 are regular singular points, and x = 9 is an irregular singular point.
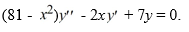 .
.Which of these statements is true?
A) x = 9 and x = -9 are both regular singular points.
B) x = 9 and x = -9 are both irregular singular points.
C) x = 0 and x = 9 are regular singular points, and x = -9 is an irregular singular point.
D) x = 0 and x = -9 are regular singular points, and x = 9 is an irregular singular point.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
53
Consider the second-order differential equation 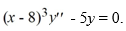 .
.
Which of these statements is true?
A) x = 0 is a regular singular point.
B) x = -8 is a regular singular point.
C) x = -8 is an irregular singular point.
D) There are no singular points.
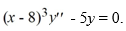 .
.Which of these statements is true?
A) x = 0 is a regular singular point.
B) x = -8 is a regular singular point.
C) x = -8 is an irregular singular point.
D) There are no singular points.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
54
x = 0 is a regular singular point for the second-order differential equation
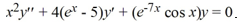 .
.
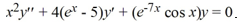 .
.
Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
55
Consider the second-order differential equation 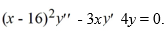 .
.
Which of these statements is true?
A) x = 4 and x = -4 are both irregular singular points.
B) x = 4 and x = -4 are both regular singular points.
C) x = -4 is a regular singular point and x = 4 is an irregular singular point.
D) x = 4 is a regular singular point and x = -4 is an irregular singular point.
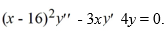 .
.Which of these statements is true?
A) x = 4 and x = -4 are both irregular singular points.
B) x = 4 and x = -4 are both regular singular points.
C) x = -4 is a regular singular point and x = 4 is an irregular singular point.
D) x = 4 is a regular singular point and x = -4 is an irregular singular point.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
56
Consider the second-order differential equation: 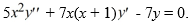 .
.
Why is C0 = 0 a regular singular point?
A) The functions and both have convergent Taylor series expansions about 0 .
B) The functions and both have convergent Taylor series expansions about 0 .
C)
D)
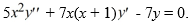 .
.Why is C0 = 0 a regular singular point?
A) The functions and both have convergent Taylor series expansions about 0 .
B) The functions and both have convergent Taylor series expansions about 0 .
C)
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
57
Consider the second-order differential equation: 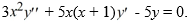 .
.
Which of these is the indicial equation?
A) (3r - 1)(r + 5) = 0
B) (3r + 1)(r - 5) = 0
C) (3r + 5)(r - 1) = 0
D) (3r - 5)(r + 1) = 0
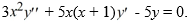 .
.Which of these is the indicial equation?
A) (3r - 1)(r + 5) = 0
B) (3r + 1)(r - 5) = 0
C) (3r + 5)(r - 1) = 0
D) (3r - 5)(r + 1) = 0

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
58
Consider the second-order differential equation: 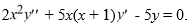 .
.
Which of these is the recurrence relation for the coefficients?
A)
B)
C)
D)
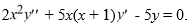 .
.Which of these is the recurrence relation for the coefficients?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
59
Consider the second-order differential equation: 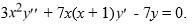 .
.
Write out the first three terms of the solution corresponding to the positive root of the indicial equation.
Y1 (x) ≈ ________
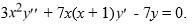 .
. Write out the first three terms of the solution corresponding to the positive root of the indicial equation.
Y1 (x) ≈ ________

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
60
Consider the second-order differential equation: 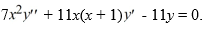 .
.
Write out the first three terms of the solution corresponding to the nonpositive root of the indicial equation.
Y2 (x) ≈ ________
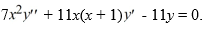 .
. Write out the first three terms of the solution corresponding to the nonpositive root of the indicial equation.
Y2 (x) ≈ ________

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
61
Consider the second-order differential equation: 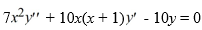 .
.
The general solution of the differential equation is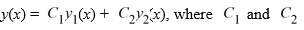 .
.
are arbitrary real constants.
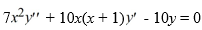 .
. The general solution of the differential equation is
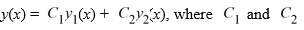 .
. are arbitrary real constants.

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
62
Consider the Bessel equation of order 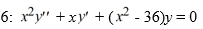 .
.
Suppose the method of Frobenius is used to determine a power series solution of the form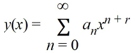 .
.
Of this differential equation. Assume a0 0.
Which of these is the indicial equation?
A) r2 - 36 = 0
B) r2- 6 = 0
C) r2+ 6 = 0
D) r2+ 36 = 0
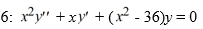 .
.Suppose the method of Frobenius is used to determine a power series solution of the form
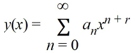 .
.Of this differential equation. Assume a0 0.
Which of these is the indicial equation?
A) r2 - 36 = 0
B) r2- 6 = 0
C) r2+ 6 = 0
D) r2+ 36 = 0

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
63
Consider the Bessel equation of order 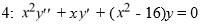 .
.
Suppose the method of Frobenius is used to determine a power series solution of the form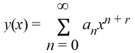 .
.
Of this differential equation. Assume a0 0.
Which of these is the recurrence relation for the coefficients?
A)
B)
C)
D)
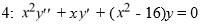 .
.Suppose the method of Frobenius is used to determine a power series solution of the form
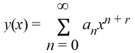 .
.Of this differential equation. Assume a0 0.
Which of these is the recurrence relation for the coefficients?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
64
Consider the Bessel equation of order 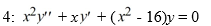 .
.
Suppose the method of Frobenius is used to determine a power series solution of the form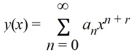 .
.
Of this differential equation. Assume a0 0.
Which of these is the explicit formula for the coefficients corresponding to the positive root of the indicial equation?
A) and
B) and
C) and
D) and
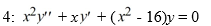 .
.Suppose the method of Frobenius is used to determine a power series solution of the form
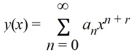 .
.Of this differential equation. Assume a0 0.
Which of these is the explicit formula for the coefficients corresponding to the positive root of the indicial equation?
A) and
B) and
C) and
D) and

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
65
Consider the Bessel equation of order 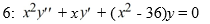 .
.
Suppose the method of Frobenius is used to determine a power series solution of the form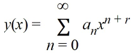 .
.
of this differential equation. Assume a0 ≠ 0.
Write the power series solution corresponding to the positive root of the indicial equation.
Y1 (x) = ________
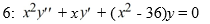 .
. Suppose the method of Frobenius is used to determine a power series solution of the form
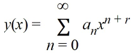 .
. of this differential equation. Assume a0 ≠ 0.
Write the power series solution corresponding to the positive root of the indicial equation.
Y1 (x) = ________

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
66
Consider the second-order differential equation 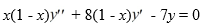 .
.
Write the differential equation in the form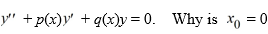 . a regular singular point for this equation?
. a regular singular point for this equation?
A) and both have convergent Taylor expansions about 0 .
B) and
C) is finite and
D) is finite and has a convergent Taylor expansion about 0 .
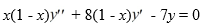 .
.Write the differential equation in the form
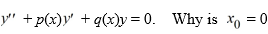 . a regular singular point for this equation?
. a regular singular point for this equation?A) and both have convergent Taylor expansions about 0 .
B) and
C) is finite and
D) is finite and has a convergent Taylor expansion about 0 .

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
67
Consider the second-order differential equation 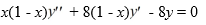 .
.
Suppose the method of Frobineius is used to determine a power series solution of the form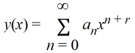 .
.
Of this differential equation. Assume a0 0. Which of these is the indicial equation?
A) r2+ 7r = 0
B)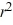 + 8r = 0
+ 8r = 0
C)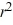 - 8r = 0
- 8r = 0
D)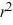 - 7r = 0
- 7r = 0
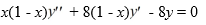 .
.Suppose the method of Frobineius is used to determine a power series solution of the form
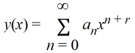 .
.Of this differential equation. Assume a0 0. Which of these is the indicial equation?
A) r2+ 7r = 0
B)
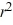 + 8r = 0
+ 8r = 0C)
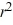 - 8r = 0
- 8r = 0D)
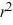 - 7r = 0
- 7r = 0
Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
68
Consider the second-order differential equation 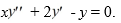 .
.
Suppose the method of Frobenius is used to determine a power series solution of the form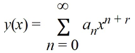 .
.
Of this differential equation. Assume a0 0.
Which of these is the indicial equation?
A) r2 + r = 0
B) r2 - r = 0
C) r2 + r - 2 = 0
D) r2 - r - 2 = 0
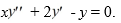 .
.Suppose the method of Frobenius is used to determine a power series solution of the form
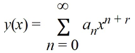 .
.Of this differential equation. Assume a0 0.
Which of these is the indicial equation?
A) r2 + r = 0
B) r2 - r = 0
C) r2 + r - 2 = 0
D) r2 - r - 2 = 0

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
69
Consider the second-order differential equation 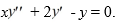 .
.
Suppose the method of Frobenius is used to determine a power series solution of the form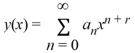 .
.
of this differential equation. Assume a0 ≠ 0.
Using the larger root of the indicial equation, write down an explicit formula for the coefficients and the corresponding power series solution.
an = ________, n ≥ 1
y1 (x) = ________
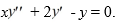 .
. Suppose the method of Frobenius is used to determine a power series solution of the form
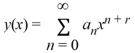 .
. of this differential equation. Assume a0 ≠ 0.
Using the larger root of the indicial equation, write down an explicit formula for the coefficients and the corresponding power series solution.
an = ________, n ≥ 1
y1 (x) = ________

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
70
Consider the second-order differential equation 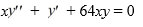 .
.
Suppose the method of Frobenius is used to determine a power series solution of this equation. The indicial equation has r = 0 as a double root. So, one of the solutions can be represented as the power series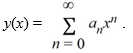 .
.
Assume a0 0.
Which of these is the recurrence relation for the coefficients?
A)
B)
C)
D)
E)
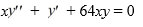 .
.Suppose the method of Frobenius is used to determine a power series solution of this equation. The indicial equation has r = 0 as a double root. So, one of the solutions can be represented as the power series
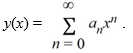 .
.Assume a0 0.
Which of these is the recurrence relation for the coefficients?
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
71
Consider the second-order differential equation 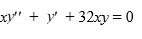 .
.
Suppose the method of Frobenius is used to determine a power series solution of this equation. The indicial equation has r = 0 as a double root. So, one of the solutions can be represented as the power series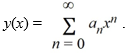 .
.
Assume a0 0.
Which of these is the explicit formula for the coefficients ?
A)
B)
C)
D)
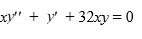 .
.Suppose the method of Frobenius is used to determine a power series solution of this equation. The indicial equation has r = 0 as a double root. So, one of the solutions can be represented as the power series
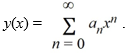 .
.Assume a0 0.
Which of these is the explicit formula for the coefficients ?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
72
Consider the second-order differential equation 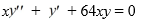 .
.
Suppose the method of Frobenius is used to determine a power series solution of this equation. The indicial equation has r = 0 as a double root. So, one of the solutions can be represented as the power series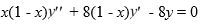 .
.
Assume a0 0.
Assuming that a0 = 1, one solution of the given differential equation is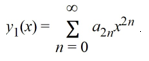 .
.
Assume x > 0. Which of these is a form of a second solution of the given differential equation, linearly independent to (x)?
A)
B)
C)
D)
E)
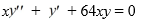 .
.Suppose the method of Frobenius is used to determine a power series solution of this equation. The indicial equation has r = 0 as a double root. So, one of the solutions can be represented as the power series
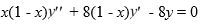 .
.Assume a0 0.
Assuming that a0 = 1, one solution of the given differential equation is
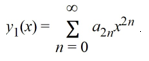 .
.Assume x > 0. Which of these is a form of a second solution of the given differential equation, linearly independent to (x)?
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
73
Consider the second-order differential equation 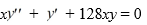 .
.
Suppose the method of Frobenius is used to determine a power series solution of this equation. The indicial equation has r = 0 as a double root. So, one of the solutions can be represented as the power series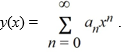 Assume a0 0.
Assume a0 0.
Assuming that a0 = 1, one solution of the given differential equation is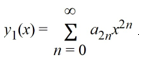
Differentiating as needed, which of these relationships is correct?
A)
B)
C)
D)
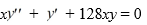 .
.Suppose the method of Frobenius is used to determine a power series solution of this equation. The indicial equation has r = 0 as a double root. So, one of the solutions can be represented as the power series
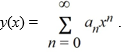 Assume a0 0.
Assume a0 0.Assuming that a0 = 1, one solution of the given differential equation is
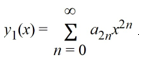
Differentiating as needed, which of these relationships is correct?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
74
Consider the second-order differential equation 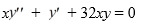 .
.
Suppose the method of Frobenius is used to determine a power series solution of this equation. The indicial equation has r = 0 as a double root. So, one of the solutions can be represented as the power series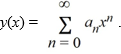 . Assume a0 ≠ 0.
. Assume a0 ≠ 0.
Assuming that a0= 1, one solution of the given differential equation is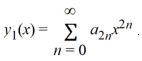
Assuming that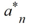 are known, what is the radius of convergence of the power series of the second solution Y2 (x)?
are known, what is the radius of convergence of the power series of the second solution Y2 (x)?
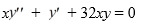 .
. Suppose the method of Frobenius is used to determine a power series solution of this equation. The indicial equation has r = 0 as a double root. So, one of the solutions can be represented as the power series
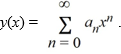 . Assume a0 ≠ 0.
. Assume a0 ≠ 0.Assuming that a0= 1, one solution of the given differential equation is
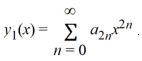
Assuming that
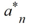 are known, what is the radius of convergence of the power series of the second solution Y2 (x)?
are known, what is the radius of convergence of the power series of the second solution Y2 (x)?
Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
75
Consider the second-order differential equation 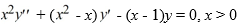 .
.
Using the method of Frobenius, which of these is the general solution of this differential equation? Assume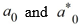 are arbitrary real constants.
are arbitrary real constants.
A)
B)
C)
D)
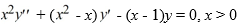 .
.Using the method of Frobenius, which of these is the general solution of this differential equation? Assume
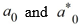 are arbitrary real constants.
are arbitrary real constants.A)
B)
C)
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
76
Consider the second-order differential equation 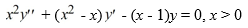 .
.
What is the radius of convergence of the series of the general solution of the differential equation?
A) 1
B) 2
C) 4
D) ?
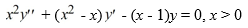 .
.What is the radius of convergence of the series of the general solution of the differential equation?
A) 1
B) 2
C) 4
D) ?

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
77
Consider the second-order differential equation 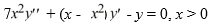 .
.
Suppose the method of Frobenius is used to determine the general solution of this differential equation.Which of these is the indicial equation about the regular singular point x = 0?
A)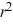 +
+ 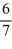 r+
r+ 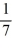 = 0
= 0
B)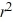 +
+ 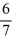 r -
r - 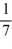 = 0
= 0
C)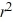 -
- 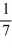 r +
r + 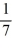 = 0
= 0
D)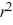 -
- 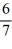 r -
r - 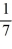 = 0
= 0
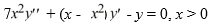 .
.Suppose the method of Frobenius is used to determine the general solution of this differential equation.Which of these is the indicial equation about the regular singular point x = 0?
A)
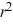 +
+ 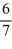 r+
r+ 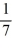 = 0
= 0B)
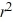 +
+ 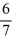 r -
r - 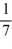 = 0
= 0C)
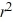 -
- 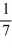 r +
r + 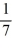 = 0
= 0D)
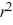 -
- 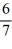 r -
r - 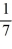 = 0
= 0
Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
78
Consider the second-order differential equation 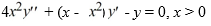 .
.
Suppose the method of Frobenius is used to determine the general solution of this differential equation.
Which of the following is the form of a pair of linearly independent solution of this differential
A)
B)
C)
D)
E)
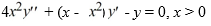 .
.Suppose the method of Frobenius is used to determine the general solution of this differential equation.
Which of the following is the form of a pair of linearly independent solution of this differential
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
79
Consider the second-order differential equation 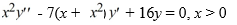 .
.
Which of these is the indicial equation about the regular singular point x = 0?
A) r2 - 9r - 16 = 0
B) r2 - 7r + 16 = 0
C) r2 + 7r + 16 = 0
D)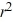 + 8r - 16 = 0
+ 8r - 16 = 0
E)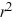 - 8r + 16 = 0
- 8r + 16 = 0
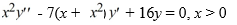 .
.Which of these is the indicial equation about the regular singular point x = 0?
A) r2 - 9r - 16 = 0
B) r2 - 7r + 16 = 0
C) r2 + 7r + 16 = 0
D)
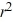 + 8r - 16 = 0
+ 8r - 16 = 0E)
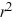 - 8r + 16 = 0
- 8r + 16 = 0
Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck
80
Consider the second-order differential equation 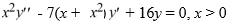 .
.
Which of the following is the form of a pair of linearly independent solutions of this differential equation?
A)
B)
C)
D)
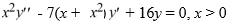 .
.Which of the following is the form of a pair of linearly independent solutions of this differential equation?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 81 flashcards in this deck.
Unlock Deck
k this deck


