Deck 4: Higher-Order Linear Differential Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/54
Play
Full screen (f)
Deck 4: Higher-Order Linear Differential Equations
1
On which of these intervals is a solution of the following differential equation sure to exist? Select all that apply.-
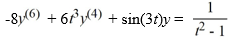 .
.
A)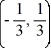
B) (0,
)
C) (- , 0)
D) (-1, 0)
E) (- , -2)F) (- , )
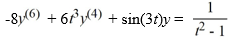 .
.A)
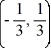
B) (0,
)
C) (- , 0)
D) (-1, 0)
E) (- , -2)F) (- , )
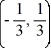
(-1, 0)
(- , -2)F) (- , )
2
On which of these intervals is a solution of the following differential equation sure to exist? Select all that apply.
![<strong>On which of these intervals is a solution of the following differential equation sure to exist? Select all that apply. .</strong> A) (4, 5] B) (0, 4) C) (0, \infty ) D) (0, 5] E) (4, \infty )F) [5, \infty )](https://storage.examlex.com/TBW1042/11eeb833_7049_5148_9020_714a388600b9_TBW1042_11.jpg) .
.
A) (4, 5]
B) (0, 4)
C) (0, )
D) (0, 5]
E) (4, )F) [5, )
![<strong>On which of these intervals is a solution of the following differential equation sure to exist? Select all that apply. .</strong> A) (4, 5] B) (0, 4) C) (0, \infty ) D) (0, 5] E) (4, \infty )F) [5, \infty )](https://storage.examlex.com/TBW1042/11eeb833_7049_5148_9020_714a388600b9_TBW1042_11.jpg) .
.A) (4, 5]
B) (0, 4)
C) (0, )
D) (0, 5]
E) (4, )F) [5, )
(4, 5]
(0, 4)
(0, 4)
3
On which of these intervals is a solution of the following differential equation sure to exist? Select all that apply.-4 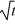
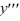 +
+ 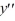 - (tan t) y = -3
- (tan t) y = -3
A) (0, )
B)
C) (0, ).
D)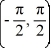
E)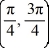
F)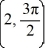
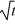
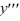 +
+ 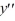 - (tan t) y = -3
- (tan t) y = -3A) (0, )
B)

C) (0, ).
D)

E)
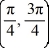
F)
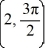

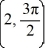
4
Compute the Wronskian W for the set of functions 2x, -3 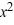 , -2
, -2 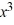 .
.
W = ________
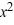 , -2
, -2 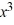 .
.W = ________

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
5
Consider the fourth-order differential equation 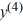 - 16y = 0. The general solution of this equation can be
- 16y = 0. The general solution of this equation can be 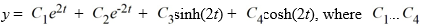 . are arbitrary real constants.
. are arbitrary real constants.
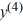 - 16y = 0. The general solution of this equation can be
- 16y = 0. The general solution of this equation can be 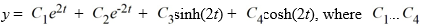 . are arbitrary real constants.
. are arbitrary real constants.
Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
6
Compute the Wronskian W for the set of functions , 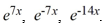 ..
..
W = ________
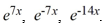 ..
..W = ________

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
7
For which of the following homogeneous differential equations is the general solution given by 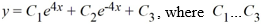 are arbitrary real constants?
are arbitrary real constants?
A)
B)
C)
D)
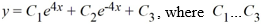 are arbitrary real constants?
are arbitrary real constants?A)
B)
C)
D)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
8
For which of the following homogeneous differential equations is the general solution given by 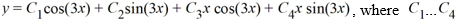
are arbitrary real constants?
A)
B)
C)
D)
E)
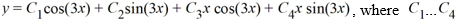
are arbitrary real constants?
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
9
For which of the following homogeneous differential equations is the general solution given by 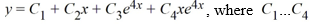 are arbitrary real constants?
are arbitrary real constants?
A)
B)
C)
D)
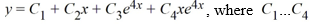 are arbitrary real constants?
are arbitrary real constants?A)
B)
C)
D)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
10
For which of the following homogeneous differential equations is the general solution given by 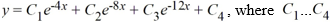 are arbitrary real constants?
are arbitrary real constants?
A)
B)
C)
D)
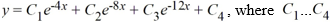 are arbitrary real constants?
are arbitrary real constants?A)
B)
C)
D)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
11
What is the least order of a homogeneous differential equation with constant coefficients for which 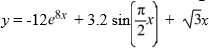 is a solution?
is a solution?
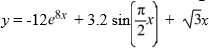 is a solution?
is a solution?
Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
12
What is the least order of a homogeneous differential equation with constant coefficients for which 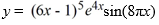 is a solution?
is a solution?
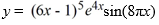 is a solution?
is a solution?
Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
13
What is the least order of a homogeneous differential equation with constant coefficients for which 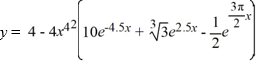 is a solution?
is a solution?
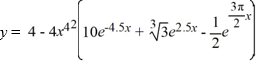 is a solution?
is a solution?
Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
14
What is the least order of a homogeneous differential equation with constant coefficients for which 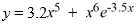 is a solution?
is a solution?
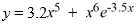 is a solution?
is a solution?
Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
15
What is the least order of a homogeneous differential equation with constant coefficients for which 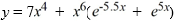 is a solution?
is a solution?
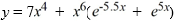 is a solution?
is a solution?
Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
16
What is the least order of a homogeneous differential equation with constant coefficients for which 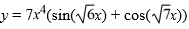 is a solution?
is a solution?
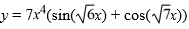 is a solution?
is a solution?
Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
17
What is the least order of a homogeneous differential equation with constant coefficients for which 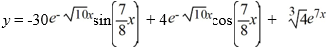 is a solution?
is a solution?
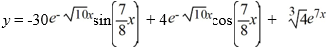 is a solution?
is a solution?
Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
18
What is the least order of a homogeneous differential equation with constant coefficients for which 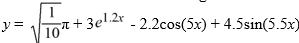 is a solution?
is a solution?
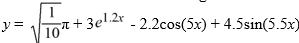 is a solution?
is a solution?
Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
19
For which of the following homogeneous differential equations is the general solution given by 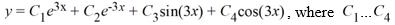
are arbitrary real constants?
A)
B)
C)
D)
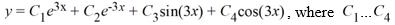
are arbitrary real constants?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
20
What is the general solution of the third-order homogeneous differential equation 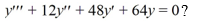
A)
B) .
C)
D) .
E)
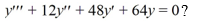
A)
B) .
C)
D) .
E)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
21
What is the general solution of the third-order homogeneous differential equation 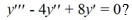 ?
?
A)
B)
C)
D)
E)
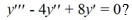 ?
?A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
22
What is the general solution of the fifth-order homogeneous differential equation 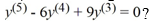
A)
B)
C)
D)
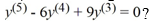
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
23
What is the general solution of the third-order homogeneous differential equation 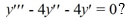
A)
B)
C)
D)
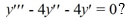
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
24
The differential equation EI(4) - ky = 0, where E, I, and k are positive constants, arises when modeling vibrating beams. What is the general solution of this equation?
A)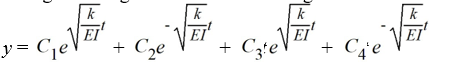
B)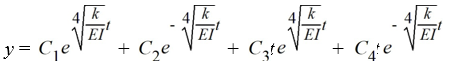
C)
D)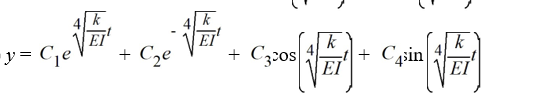
A)
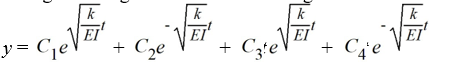
B)
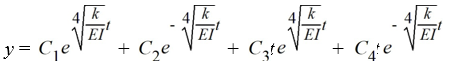
C)

D)
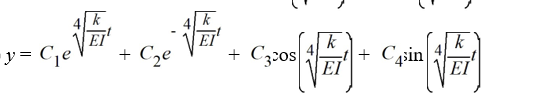

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
25
Suppose a fourth-order homogeneous linear differential equation with constant coefficients has these characteristic roots: -8.8, 8.8, 10i, -10i
Which of the following terms are part of the general solution of this equation? Here, C denotes an arbitrary real constant.
Select all that apply.
A)
B)
C)
D)
E)
F)
Which of the following terms are part of the general solution of this equation? Here, C denotes an arbitrary real constant.
Select all that apply.
A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
26
Suppose a seventh-order homogeneous linear differential equation with constant coefficients has these characteristic roots: 0, 0, 0, 3 - i, 3 +  i, -
i, - 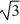 i,
i, 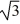 i
i
Which of the following terms are part of the general solution of this equation? Here, C denotes an arbitrary real constant.Select all that apply.
A)
B)
C)
D)
E)
F)
G)
H)
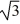 i, -
i, - 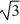 i,
i, 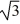 i
iWhich of the following terms are part of the general solution of this equation? Here, C denotes an arbitrary real constant.Select all that apply.
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
27
Suppose a ninth-order homogeneous linear differential equation with constant coefficients has these characteristic roots: -6i, -6i, 6i, 6i, 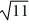 , -
, - 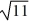 , -
, - 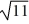 ,
, 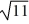 -6.2
-6.2
Which of the following terms are part of the general solution of this equation? Here, C denotes an arbitrary real constant.Select all that apply.
A)
B)
C)
D)
E)
F)
G)
H)
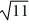 , -
, - 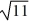 , -
, - 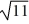 ,
, 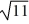 -6.2
-6.2Which of the following terms are part of the general solution of this equation? Here, C denotes an arbitrary real constant.Select all that apply.
A)
B)
C)
D)
E)
F)
G)
H)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
28
What is the general solution of the third-order linear homogeneous differential equation 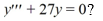
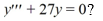

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
29
What is the general solution of the third-order linear homogeneous differential equation 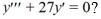
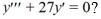

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
30
What is the general solution of the third-order linear homogeneous differential equation 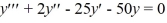 ?
?
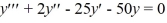 ?
?
Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
31
What is the general solution of the fourth-order linear homogeneous differential equation 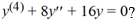
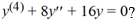

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the following initial value problem:
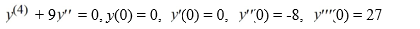
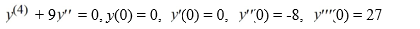

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the following initial value problem:
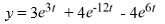
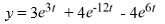

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the following initial value problem:
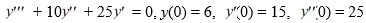
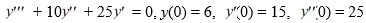

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
35
What is the form of a particular solution of the following nonhomogeneous differential equation?
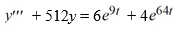
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)
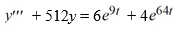
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
36
What is the form of a particular solution of the following nonhomogeneous differential equation?
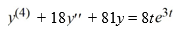
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)
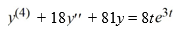
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
37
What is the form of a particular solution of the following nonhomogeneous differential equation?
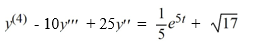
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)
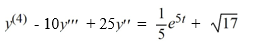
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
38
What is the form of a particular solution of the following nonhomogeneous differential equation?
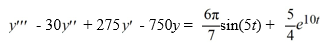
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)
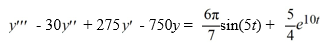
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
39
What is the form of a particular solution of the following nonhomogeneous differential equation?
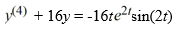
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)
E)
F)
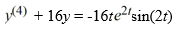
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
40
What is the form of a particular solution of the following nonhomogeneous differential equation?
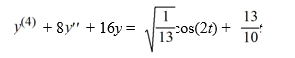
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)
E)
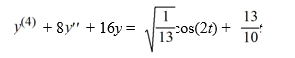
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
41
What is the form of a particular solution of the following nonhomogeneous differential equation?-
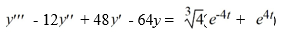
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)
E)
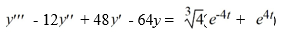
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
42
What is the form of a particular solution of the following nonhomogeneous differential equation?
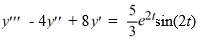
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)
E)
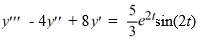
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
43
What is the form of a particular solution of the following nonhomogeneous differential equation?
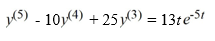
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)
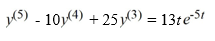
All capital letters in the choices represent arbitrary real constants.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
44
What is the form of a particular solution of the following nonhomogeneous differential equation?
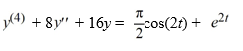
Use capital letters A, B, C, ... to represent arbitrary real constants. Do not actually solve for the constants.
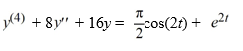
Use capital letters A, B, C, ... to represent arbitrary real constants. Do not actually solve for the constants.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
45
What is the form of a particular solution of the following nonhomogeneous differential equation?
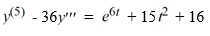
Use capital letters A, B, C, ... to represent arbitrary real constants. Do not actually solve for the constants.
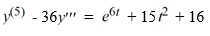
Use capital letters A, B, C, ... to represent arbitrary real constants. Do not actually solve for the constants.

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
46
Consider the nonhomogeneous differential equation 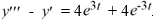 The functions
The functions 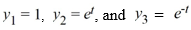 form a fundamental set of solutions of the corresponding homogeneous equation
form a fundamental set of solutions of the corresponding homogeneous equation 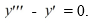
Compute the Wronskian,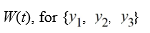
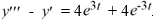 The functions
The functions 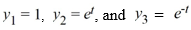 form a fundamental set of solutions of the corresponding homogeneous equation
form a fundamental set of solutions of the corresponding homogeneous equation 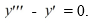
Compute the Wronskian,
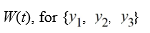

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
47
Consider the nonhomogeneous differential equation 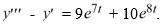 The functions
The functions 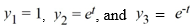 form a fundamental set of solutions of the corresponding homogeneous equation
form a fundamental set of solutions of the corresponding homogeneous equation 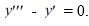
Suppose the method of variation of parameters is to be used to find a particular solution Yp of the nonhomogeneous differential equation. Then,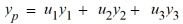 for appropriately-chosen functions
for appropriately-chosen functions 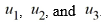 As part of the process of forming this solution, find the following quantities.
As part of the process of forming this solution, find the following quantities.
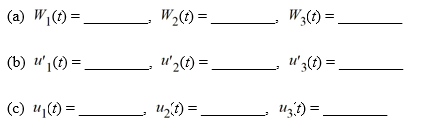
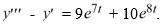 The functions
The functions 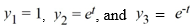 form a fundamental set of solutions of the corresponding homogeneous equation
form a fundamental set of solutions of the corresponding homogeneous equation 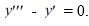
Suppose the method of variation of parameters is to be used to find a particular solution Yp of the nonhomogeneous differential equation. Then,
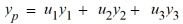 for appropriately-chosen functions
for appropriately-chosen functions 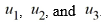 As part of the process of forming this solution, find the following quantities.
As part of the process of forming this solution, find the following quantities.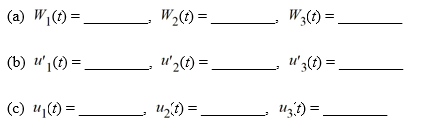

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
48
Consider the following third-order nonhomogeneous differential equation:
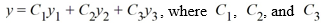
Find three functions Y1 , Y1 and Y1 that form a fundamental set and are such that the general solution of the corresponding homogeneous equation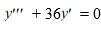 is given by
is given by 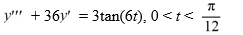 are arbitrary real constants.
are arbitrary real constants.
Y1 = ________, Y2 = ________, Y3 = ________
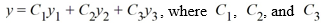
Find three functions Y1 , Y1 and Y1 that form a fundamental set and are such that the general solution of the corresponding homogeneous equation
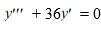 is given by
is given by 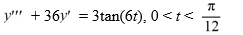 are arbitrary real constants.
are arbitrary real constants.Y1 = ________, Y2 = ________, Y3 = ________

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
49
Consider the following third-order nonhomogeneous differential equation:
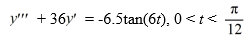
Compute the Wronskian, W(t), for the set of functions Y1 ,Y2 , and Y3 that form a fundamental set and are such that the general solution of the corresponding homogeneous equation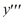 + 36
+ 36 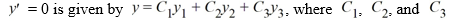 are arbitrary real constants.
are arbitrary real constants.
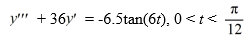
Compute the Wronskian, W(t), for the set of functions Y1 ,Y2 , and Y3 that form a fundamental set and are such that the general solution of the corresponding homogeneous equation
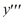 + 36
+ 36 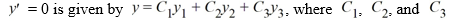 are arbitrary real constants.
are arbitrary real constants.
Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
50
Consider the following third-order nonhomogeneous differential equation:
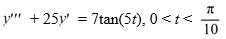
Suppose the method of variation of parameters is to be used to find a particular solution of the nonhomogeneous differential equation. Then,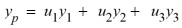 for appropriately-chosen functions u1 , u2, and u3 . As part of the process of forming this solution, find the following quantities.
for appropriately-chosen functions u1 , u2, and u3 . As part of the process of forming this solution, find the following quantities.
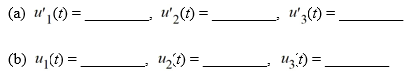
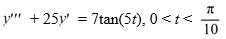
Suppose the method of variation of parameters is to be used to find a particular solution of the nonhomogeneous differential equation. Then,
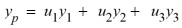 for appropriately-chosen functions u1 , u2, and u3 . As part of the process of forming this solution, find the following quantities.
for appropriately-chosen functions u1 , u2, and u3 . As part of the process of forming this solution, find the following quantities.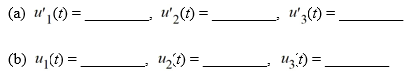

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
51
Use the method of variation of parameters to solve the following third-order nonhomogeneous differential equation:
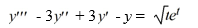
A)
B)
C)
D)
E)
F)
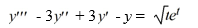
A)
B)
C)
D)
E)
F)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
52
Compute the Wronskian W for the set of functions 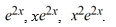
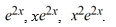

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
53
What is the general solution of the third-order homogeneous Cauchy Euler differential equation 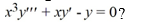
A)
B)
C)
D)
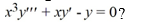
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck
54
What is the general solution of the third-order homogeneous Cauchy Euler differential equation
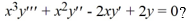
A)
B)
C)
D)
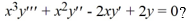
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 54 flashcards in this deck.
Unlock Deck
k this deck


