Deck 7: Systems of Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/80
Play
Full screen (f)
Deck 7: Systems of Equations
1
Decide whether or not the ordered pair is a solution of the system.
-
-
True
2
Decide whether or not the ordered pair is a solution of the system.
-
-
False
3
Decide whether or not the ordered pair is a solution of the system.
-
-
True
4
Decide whether or not the ordered pair is a solution of the system.
-
-

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
5
Decide whether or not the ordered pair is a solution of the system.
-
-

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
6
Decide whether or not the ordered pair is a solution of the system.
-
-

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
7
Decide whether or not the ordered pair is a solution of the system.
-
-

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
8
Decide whether or not the ordered pair is a solution of the system.
-
-

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
9
Solve the system by graphing.
-x + y = 7
X - y = -3
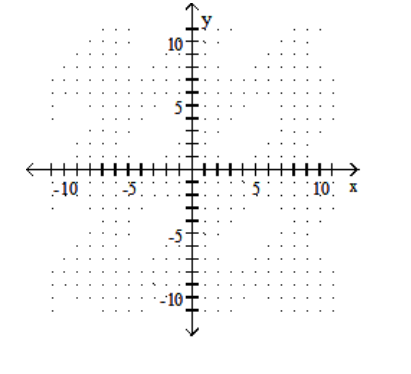
A)
B) Infinite number of solutions
C) No solution
D)
-x + y = 7
X - y = -3

A)
B) Infinite number of solutions
C) No solution
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
10
Solve the system by graphing.
-
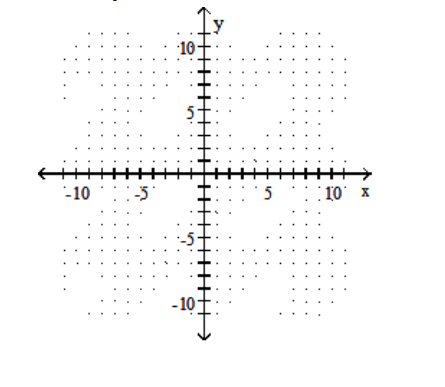
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
11
Solve the system by graphing.
-
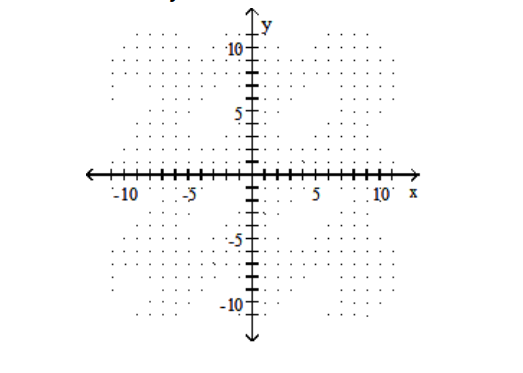
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
12
Solve the system by graphing.
-
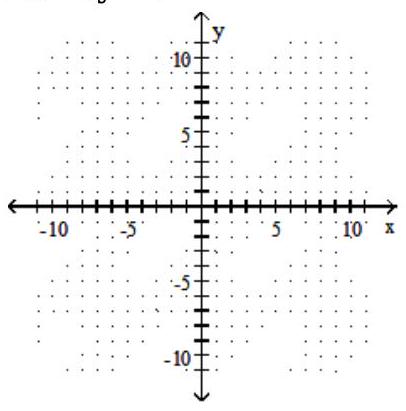
A)
B)
C) No solution
D)
-

A)
B)
C) No solution
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
13
Solve the system by graphing.
-
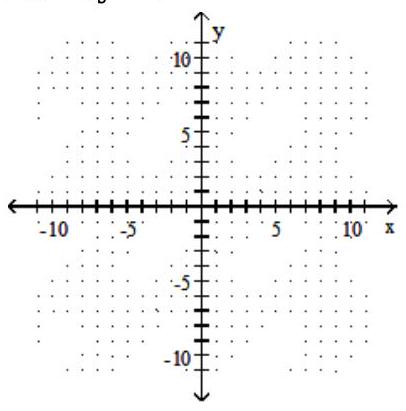
A) No solution
B)
C)
D)
-

A) No solution
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
14
Solve the system by graphing.
-
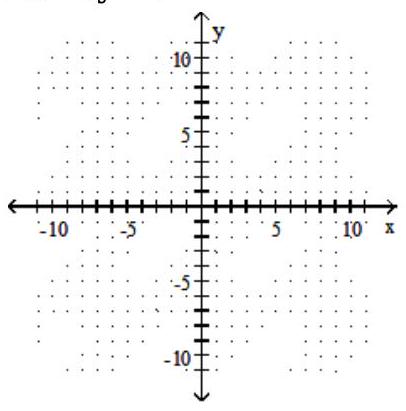
A) No solution
B)
C) Infinite number of solutions
D)
-

A) No solution
B)
C) Infinite number of solutions
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
15
Solve the system by graphing.
-
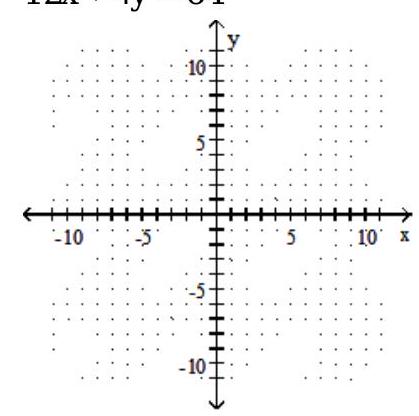
A) Infinite number of solutions
B)
C) No solution
D)
-

A) Infinite number of solutions
B)
C) No solution
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
16
Solve the system by graphing.
-
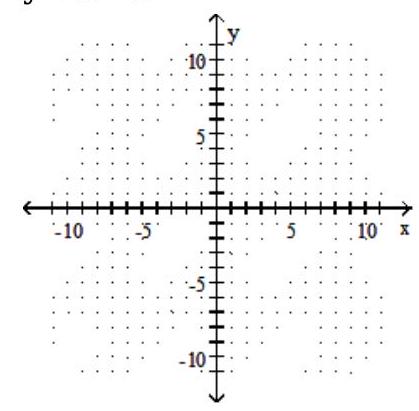
A)
B) Infinite number of solutions
C) No solution
D)
-

A)
B) Infinite number of solutions
C) No solution
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
17
Solve the system by graphing.
-x = 2
Y = 1
A)
B) No solution
C)
D) Infinitely many solutions
-x = 2
Y = 1

A)
B) No solution
C)
D) Infinitely many solutions

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
18
Solve using the substitution method.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
19
Solve using the substitution method.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
20
Solve by the substitution method.
-
A) No solution
B)
C)
D)
-
A) No solution
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
21
Solve by the substitution method.
-
A)
B)
C) No solution
D)
-
A)
B)
C) No solution
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
22
Solve by the substitution method.
-
A)
B) No solution
C)
D)
-
A)
B) No solution
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
23
Solve by the substitution method.
-
A)
B)
C) No solution
D)
-
A)
B)
C) No solution
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
24
Solve by the substitution method.
-
A)
B)
C) No solution
D)
-
A)
B)
C) No solution
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
25
Solve by the substitution method.
-
A)
B) No solution
C)
D)
-
A)
B) No solution
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
26
Solve by the substitution method.
-
A)
B) No solution
C)
D)
-
A)
B) No solution
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
27
Solve by the substitution method.
-
A)
B)
C)
D) No solution
-
A)
B)
C)
D) No solution

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
28
Solve by the substitution method.
-
A) Infinite number of solutions
B)
C)
D)
-
A) Infinite number of solutions
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
29
Solve the problem.
-The sum of two numbers is 45 and their difference is 9 . Find the numbers.
A) 27 and 18
B) 37 and 8
C) 25 and 20
D) 20 and 29
-The sum of two numbers is 45 and their difference is 9 . Find the numbers.
A) 27 and 18
B) 37 and 8
C) 25 and 20
D) 20 and 29

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
30
Solve the problem.
-The difference between two numbers is 2 . Three times the smaller number minus five times the larger is -34 . What are the numbers?
A) 13 and 15
B) 14 and 16
C) 11 and 13
D) 12 and 14
-The difference between two numbers is 2 . Three times the smaller number minus five times the larger is -34 . What are the numbers?
A) 13 and 15
B) 14 and 16
C) 11 and 13
D) 12 and 14

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the problem.
-Two angles have a sum of . Their difference is . Find the angles.
A) and
B) and
C) and
D) and
-Two angles have a sum of . Their difference is . Find the angles.
A) and
B) and
C) and
D) and

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the problem.
-The sum of two angles is . One angle is less than twice the other. Find the angles.
A) and
B) and
C) and
D) and
-The sum of two angles is . One angle is less than twice the other. Find the angles.
A) and
B) and
C) and
D) and

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the problem.
-The perimeter of a rectangle is . One side is longer than the other side. Find the lengths of the sides.
A)
B)
C)
D)
-The perimeter of a rectangle is . One side is longer than the other side. Find the lengths of the sides.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the problem.
-The perimeter of a rectangle is . If the width were doubled and the length were increased by , the perimeter would be . What are the length and width of the rectangle?
A) width , length
B) width , length
C) width , length
D) width , length
-The perimeter of a rectangle is . If the width were doubled and the length were increased by , the perimeter would be . What are the length and width of the rectangle?
A) width , length
B) width , length
C) width , length
D) width , length

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
35
Solve the problem.
-The perimeter of a triangle is . The triangle is isosceles now, but if its base were lengthened by and each leg were shortened by , it would be equilateral. Find the base of the original triangle.
A)
B)
C)
D)
-The perimeter of a triangle is . The triangle is isosceles now, but if its base were lengthened by and each leg were shortened by , it would be equilateral. Find the base of the original triangle.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
36
Solve the problem.
-x+y=-11
X-y=3
A) No solution
B)
C)
D)
-x+y=-11
X-y=3
A) No solution
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
37
Solve using the elimination method.
-
A)
B)
C)
D) No solution
-
A)
B)
C)
D) No solution

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
38
Solve using the elimination method.
-
A)
B)
C) No solution
D)
-
A)
B)
C) No solution
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
39
Solve using the elimination method.
-
A)
B)
C)
D) No solution
-
A)
B)
C)
D) No solution

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
40
Solve using the elimination method.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
41
Solve using the elimination method.
-
A)
B) Infinite number of solutions
C)
D) No solution
-
A)
B) Infinite number of solutions
C)
D) No solution

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
42
Solve by elimination.
-
A)
B)
C)
D) No solution
-
A)
B)
C)
D) No solution

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
43
Solve by elimination.
-
A)
B)
C) No solution
D)
-
A)
B)
C) No solution
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
44
Solve by elimination.
-
A)
B) No solution
C)
D)
-
A)
B) No solution
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
45
Solve by elimination.
-
A)
B)
C) No solution
D)
-
A)
B)
C) No solution
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
46
Solve by elimination.
-
A)
B) No solution
C)
D)
-
A)
B) No solution
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
47
Solve by elimination.
-
A)
B)
C)
D) No solution
-
A)
B)
C)
D) No solution

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
48
Solve by elimination.
-
A)
B) Infinite number of solutions
C) No solution
D)
-
A)
B) Infinite number of solutions
C) No solution
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
49
Solve by elimination.
-
A) Infinite number of solutions
B) No solution
C)
D)
-
A) Infinite number of solutions
B) No solution
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
50
Solve by elimination.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
51
Solve by elimination.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
52
Solve the problem.
-Two angles are supplementary, and one is more than three times the other. Find the smaller angle.
A)
B)
C)
D)
-Two angles are supplementary, and one is more than three times the other. Find the smaller angle.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
53
Solve the problem.
-In a right triangle, one acute angle is more than twice the other. Find each acute angle.
A) and
B) and
C) and
D) and
-In a right triangle, one acute angle is more than twice the other. Find each acute angle.
A) and
B) and
C) and
D) and

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
54
Solve the problem.
-Two angles are supplementary, and one is more than six times the other. Find the larger angle.
A)
B)
C)
D)
-Two angles are supplementary, and one is more than six times the other. Find the larger angle.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
55
Solve the problem.
-Best Rentals charges a daily fee plus a mileage fee for renting its cars. Barney was charged for 3 days and 300 miles, while Mary was charged for 5 days and 600 miles. What does Best Rental charge per day and per mile?
A) per day and per mile
B) per day and per mile
C) per day and per mile
D) per day and per mile
-Best Rentals charges a daily fee plus a mileage fee for renting its cars. Barney was charged for 3 days and 300 miles, while Mary was charged for 5 days and 600 miles. What does Best Rental charge per day and per mile?
A) per day and per mile
B) per day and per mile
C) per day and per mile
D) per day and per mile

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
56
Solve the problem.
-There were 33,000 people at a ball game in Los Angeles. The day's receipts were . How many people paid for reserved seats and how many paid for general admission?
A) 10,000 paid and 23,000 paid
B) 13,000 paid and 20,000 paid
C) 20,000 paid and 13,000 paid
D) 23,000 paid and 10,000 paid
-There were 33,000 people at a ball game in Los Angeles. The day's receipts were . How many people paid for reserved seats and how many paid for general admission?
A) 10,000 paid and 23,000 paid
B) 13,000 paid and 20,000 paid
C) 20,000 paid and 13,000 paid
D) 23,000 paid and 10,000 paid

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
57
Solve the problem.
-There were 480 people at a play. The admission price was for adults and for children. The admission receipts were . How many adults and how many children attended?
A) 185 adults and 295 children
B) 220 adults and 260 children
C) 260 adults and 220 children
D) 110 adults and 370 children
-There were 480 people at a play. The admission price was for adults and for children. The admission receipts were . How many adults and how many children attended?
A) 185 adults and 295 children
B) 220 adults and 260 children
C) 260 adults and 220 children
D) 110 adults and 370 children

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
58
Solve the problem.
-A salesman sold more than the rest of the sales staff. If the sales total for the day was , how much did the rest of the sales staff sell?
A)
B)
C)
D)
-A salesman sold more than the rest of the sales staff. If the sales total for the day was , how much did the rest of the sales staff sell?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
59
Solve the problem.
-Joe has a collection of nickels and dimes that is worth . If the number of dimes were doubled and the number of nickels were increased by 15 , the value of the coins would be . How many dimes does he have?
A) 15 dimes
B) 21 dimes
C) 10 dimes
D) 47 dimes
-Joe has a collection of nickels and dimes that is worth . If the number of dimes were doubled and the number of nickels were increased by 15 , the value of the coins would be . How many dimes does he have?
A) 15 dimes
B) 21 dimes
C) 10 dimes
D) 47 dimes

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the problem.
-Mrs. Boyd has a desk full of quarters and nickels. If she has a total of 20 coins with a total face value of , how many of the coins are nickels?
A) 7 nickels
B) 15 nickels
C) 12 nickels
D) 13 nickels
-Mrs. Boyd has a desk full of quarters and nickels. If she has a total of 20 coins with a total face value of , how many of the coins are nickels?
A) 7 nickels
B) 15 nickels
C) 12 nickels
D) 13 nickels

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
61
Solve the problem.
-Andy has 34 coins made up of quarters and half dollars, and their total value is . How many quarters does he have?
A) 20 quarters
B) 19 quarters
C) 22 quarters
D) 14 quarters
-Andy has 34 coins made up of quarters and half dollars, and their total value is . How many quarters does he have?
A) 20 quarters
B) 19 quarters
C) 22 quarters
D) 14 quarters

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
62
Solve the problem.
-Ron and Kathy are ticket- sellers at their class play, Ron handling student tickets that sell for each and Kathy selling adult tickets for each. If their total income for 38 tickets was , how many did Ron sell?
A) 18 tickets
B) 23 tickets
C) 22 tickets
D) 20 tickets
-Ron and Kathy are ticket- sellers at their class play, Ron handling student tickets that sell for each and Kathy selling adult tickets for each. If their total income for 38 tickets was , how many did Ron sell?
A) 18 tickets
B) 23 tickets
C) 22 tickets
D) 20 tickets

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
63
Solve the problem.
-Helen Weller invested in an account that pays simple interest. How much additional money must be invested in an account that pays 15\% simple interest so that the total interest is equal to the interest on the two investments at the rate of ?
A)
B)
C)
D)
-Helen Weller invested in an account that pays simple interest. How much additional money must be invested in an account that pays 15\% simple interest so that the total interest is equal to the interest on the two investments at the rate of ?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
64
Solve the problem.
-Roberto invested some money at , and then invested more than twice this amount at . His total annual income from the two investments was . How much was invested at ?
A)
B)
C)
D)
-Roberto invested some money at , and then invested more than twice this amount at . His total annual income from the two investments was . How much was invested at ?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the problem.
-Tim and Judy mix two kinds of feed for pedigreed dogs. They wish to make 21 pounds of feed worth per pound by mixing one kind worth per pound with another worth per pound. How many pounds of the cheaper kind should they use in the mix? Round to the nearest whole pound if necessary.
A) 10 pounds
B) 12 pounds
C) 16 pounds
D) 11 pounds
-Tim and Judy mix two kinds of feed for pedigreed dogs. They wish to make 21 pounds of feed worth per pound by mixing one kind worth per pound with another worth per pound. How many pounds of the cheaper kind should they use in the mix? Round to the nearest whole pound if necessary.
A) 10 pounds
B) 12 pounds
C) 16 pounds
D) 11 pounds

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
66
Solve the problem.
-Ellen wishes to mix candy worth per pound with candy worth per pound to form 16 pounds of a mixture worth per pound. How many pounds of the more expensive candy should she use?
A) 12 pounds
B) 9 pounds
C) 11 pounds
D) 7 pounds
-Ellen wishes to mix candy worth per pound with candy worth per pound to form 16 pounds of a mixture worth per pound. How many pounds of the more expensive candy should she use?
A) 12 pounds
B) 9 pounds
C) 11 pounds
D) 7 pounds

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
67
Solve the problem.
-A contractor mixes concrete from bags of pre- mix for small jobs. How many bags with cement should he mix with 7 bags of cement to produce a mix containing cement?
A) 21 bags
B) 11 bags
C) 16 bags
D) 9 bags
-A contractor mixes concrete from bags of pre- mix for small jobs. How many bags with cement should he mix with 7 bags of cement to produce a mix containing cement?
A) 21 bags
B) 11 bags
C) 16 bags
D) 9 bags

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
68
Solve the problem.
-How many liters of a alcohol solution must be mixed with 60 liters of a solution to get a solution?
A)
B)
C)
D)
-How many liters of a alcohol solution must be mixed with 60 liters of a solution to get a solution?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
69
Solve the problem.
-In a chemistry class, 5 liters of a silver iodide solution must be mixed with a solution to get a solution. How many liters of the solution are needed?
A)
B)
C)
D)
-In a chemistry class, 5 liters of a silver iodide solution must be mixed with a solution to get a solution. How many liters of the solution are needed?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
70
Solve the problem.
-A merchant has coffee worth a pound that she wishes to mix with 80 pounds of coffee worth 70 a pound to get a mixture that can be sold for a pound. How many pounds of the coffee should be used?
A)
B)
C)
D)
-A merchant has coffee worth a pound that she wishes to mix with 80 pounds of coffee worth 70 a pound to get a mixture that can be sold for a pound. How many pounds of the coffee should be used?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
71
Solve the problem.
-A boat traveled for with a 3- current to reach a picnic area. The return trip against the same current took . Find the speed of the boat in still water.
A)
B)
C)
D)
-A boat traveled for with a 3- current to reach a picnic area. The return trip against the same current took . Find the speed of the boat in still water.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
72
Solve the problem.
-Kevin walks and jogs to his favorite coffee shop to study each weekend. He averages walking and jogging. The distance from his home to the coffee shop is , and he makes the trip in . How long does Kevin jog?
A)
B)
C)
D)
-Kevin walks and jogs to his favorite coffee shop to study each weekend. He averages walking and jogging. The distance from his home to the coffee shop is , and he makes the trip in . How long does Kevin jog?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
73
Solve the problem.
-An airplane took to fly against a head wind. The return trip with the same wind took 1 . Find the speed of the plane in still air.
A)
B)
C)
D)
-An airplane took to fly against a head wind. The return trip with the same wind took 1 . Find the speed of the plane in still air.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
74
Solve the problem.
-Rachael's bike got a flat tire and she must walk the rest of the way to work. The bike was being ridden at , and Rachael walks at a speed of . The distanœ from home to work is , and the total time for the trip was . How far did she have to walk?
A)
B)
C)
D)
-Rachael's bike got a flat tire and she must walk the rest of the way to work. The bike was being ridden at , and Rachael walks at a speed of . The distanœ from home to work is , and the total time for the trip was . How far did she have to walk?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
75
Solve the problem.
-Two cars leave town at the same time going in the same direction. One travels at and the other travels at . In how many hours will they be apart?
A)
B)
C)
D)
-Two cars leave town at the same time going in the same direction. One travels at and the other travels at . In how many hours will they be apart?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
76
Solve the problem.
-A private airplane leaves an airport and flies due east at . Two hours later, a jet leaves the same airport and flies due east at . When will the jet overtake the plane?
A)
B)
C)
D)
-A private airplane leaves an airport and flies due east at . Two hours later, a jet leaves the same airport and flies due east at . When will the jet overtake the plane?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
77
Solve the problem.
-The speed of a stream is . If a boat travels 40 miles downstream in the same time that it takes to travel 20 miles upstream, what is the speed of the boat in still water?
A)
B)
C)
D)
-The speed of a stream is . If a boat travels 40 miles downstream in the same time that it takes to travel 20 miles upstream, what is the speed of the boat in still water?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
78
Solve the problem.
-A plane flies 420 miles with the wind and 320 miles against the wind in the same length of time. If the speed of the wind is , what is the speed of the plane in still air?
A)
B)
C)
D)
-A plane flies 420 miles with the wind and 320 miles against the wind in the same length of time. If the speed of the wind is , what is the speed of the plane in still air?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
79
Solve the problem.
-From a point on a river, two boats are driven in opposite directions, one at 9 miles per hour and the other at 6 miles per hour. In how many hours will they be 60 miles apart?
A)
B)
C)
D)
-From a point on a river, two boats are driven in opposite directions, one at 9 miles per hour and the other at 6 miles per hour. In how many hours will they be 60 miles apart?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck
80
Solve the problem.
-Candy and Delvis are riding bicycles in the same direction. Candy is traveling at the speed of 6 miles per hour, and Delvis is traveling at the speed of 12 miles per hour. In 4 hours what is the distance between them?
A)
B)
C)
D)
-Candy and Delvis are riding bicycles in the same direction. Candy is traveling at the speed of 6 miles per hour, and Delvis is traveling at the speed of 12 miles per hour. In 4 hours what is the distance between them?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 80 flashcards in this deck.
Unlock Deck
k this deck


