Deck 11: Polynomial and Rational Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/145
Play
Full screen (f)
Deck 11: Polynomial and Rational Functions
1
Is a power function?
False
2
Is a power function?
True
3
The power function through the points and is , where -----------and . Round the second answer to 3 decimal places.
Part A:
Part B:
Part B:
4
Suppose is directly proportional to . If when , what is the value of when is 2 ?

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
5
The formula for the power function whose values are in the following table is , where --------- and -----------
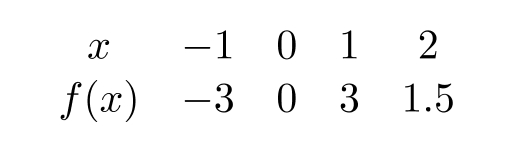

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
6
According to one advertisement, Burger King's all-beef hamburger patties have more beef than McDonald's all-beef hamburger patties. If both chains serve circular patties of the same thickness, then the diameter of Burger King's patties, , will be directly proportional to the diameter of McDonald's patties, . Which of the following formulas express as a function of ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
7
The volume occupied by a fixed quantity of gas such as oxygen is inversely proportional to its pressure, provided that its temperature is held constant. Suppose that a quantity of oxygen occupies a 110 liter volume at a pressure of 12 atmospheres. If the temperature of the oxygen does not change, how many liters will it occupy if its pressure rises to 17 atmospheres? Round to 1 decimal place.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
8
When temperature is held constant, the pressure and volume of a quantity of gas are inversely proportional (Boyle's Law). The following figure shows this relationship for a particular gas. Find a formula for in terms of and use it to find when is 7 . Round to 2 decimal places.
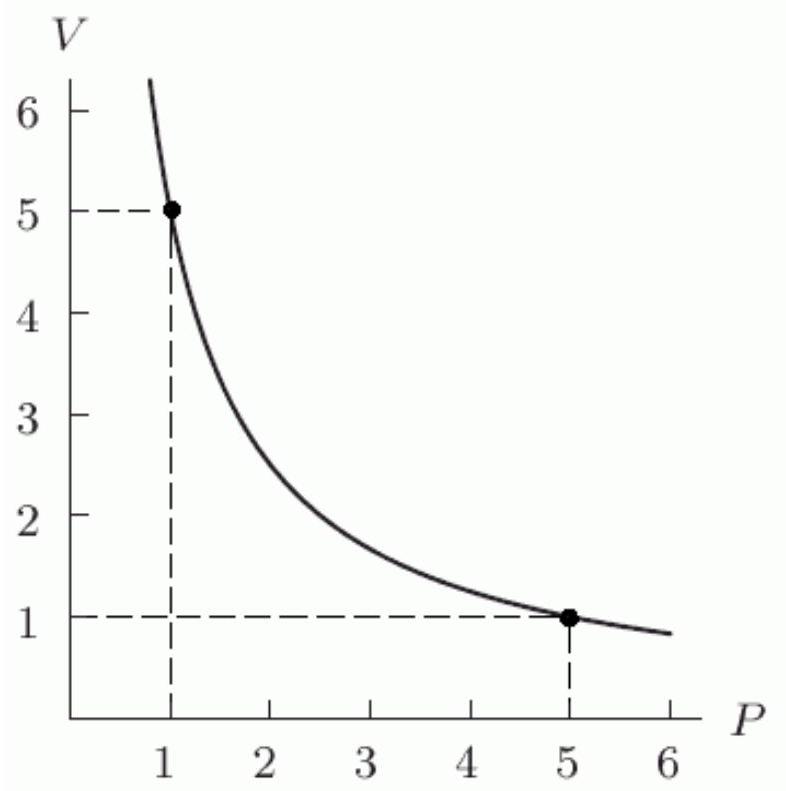


Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
9
Poiseuille's law says that the rate at which blood is flowing through a blood vessel of radius is proportional to . For medical reasons, we want to know how a reduction in the radius of a blood vessel affects the blood flow. If the radius of the blood vessel decreases by , by what percentage does the blood flow decrease? Round to the nearest whole percent.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
10
Which of the following graphs show being proportional to the square of ?
A)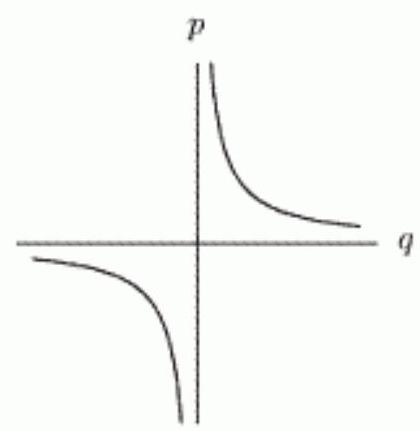
B)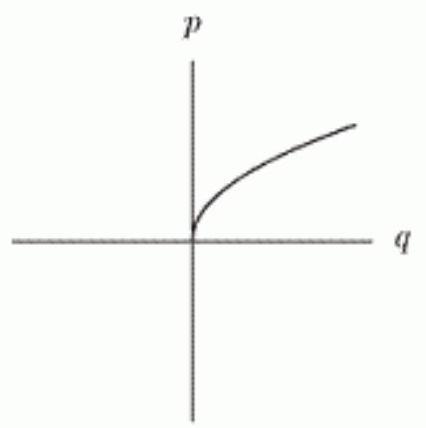
C)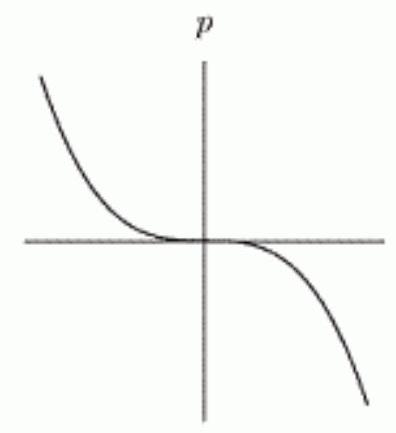
D)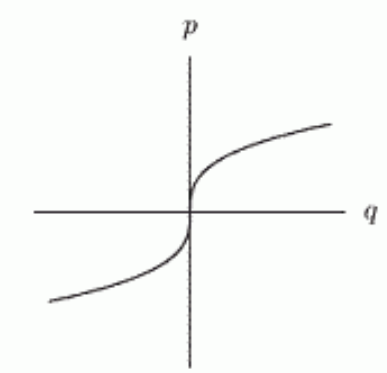
E)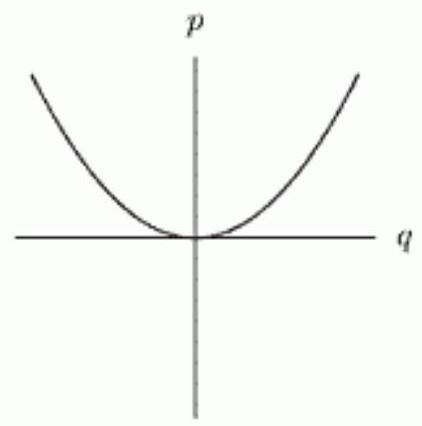
F)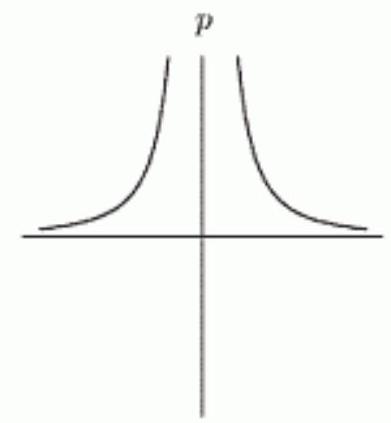
A)

B)

C)

D)

E)

F)


Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
11
The figure below shows the graphs of two power functions, and . The formula for is , where -------- and -------------
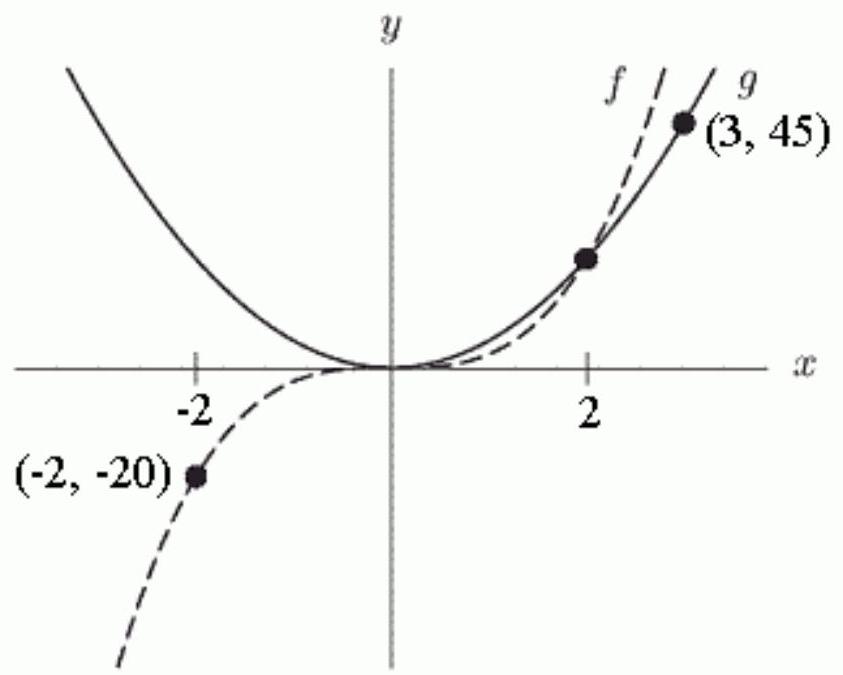


Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
12
The following figure gives the graphs of and .
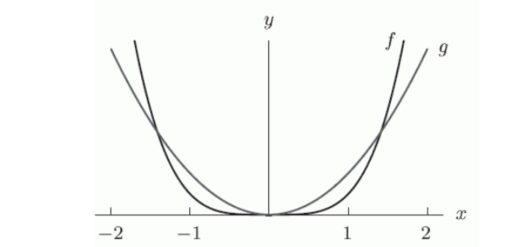
Which is smaller, or ?

Which is smaller, or ?

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose that , and are integers and that is positive and even, is positive and odd, is negative and even, and is negative and odd. Which of the following graphs could correspond to the power function ? If none of the graphs correspond to the function, enter "none".
A)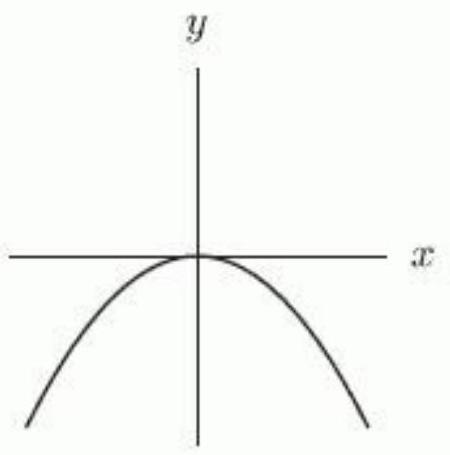
B)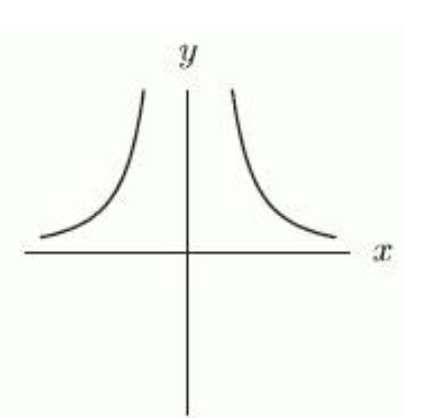
C)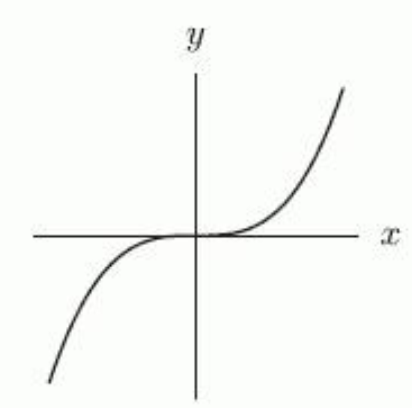
D)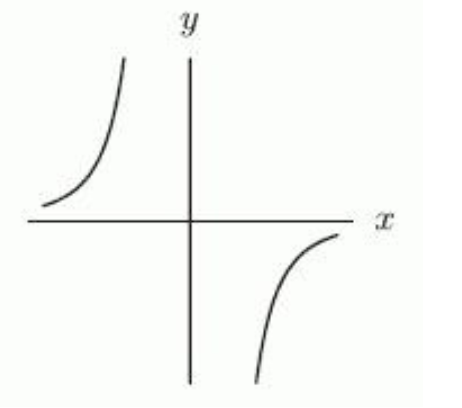
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
14
The following figure shows the graph of a power function, , whose formula has the form . Which of the following statements are true? Mark all that apply.
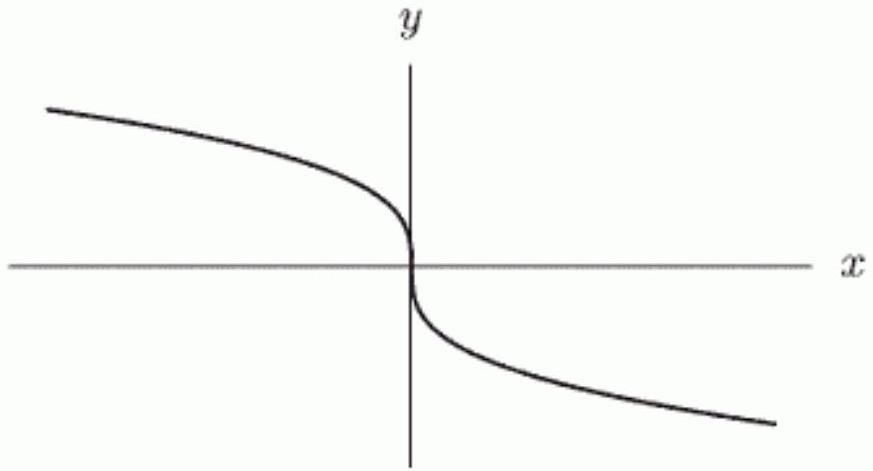
A)
B)
C) must be an integer
D)
E) P
F)

A)
B)
C) must be an integer
D)
E) P
F)

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
15
The following figure gives the graphs of and .
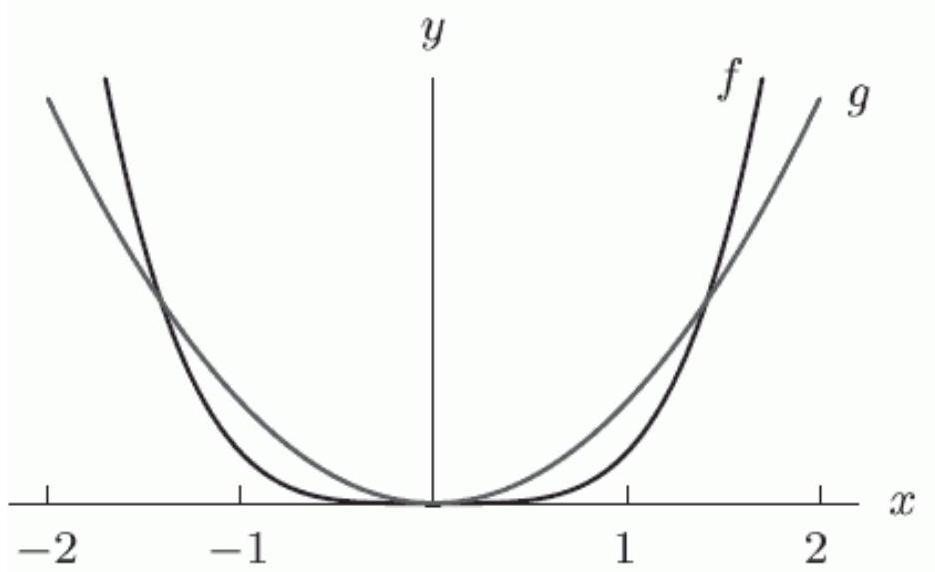
If , what is

If , what is

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
16
Let satisfy the conditions , and . Which of the following must be true?
A) is odd
B) is even
C) is positive
D) is negative
E) is positive
F) is negative
A) is odd
B) is even
C) is positive
D) is negative
E) is positive
F) is negative

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
17
Let and be graphed in the following figure. Which of the following is true?
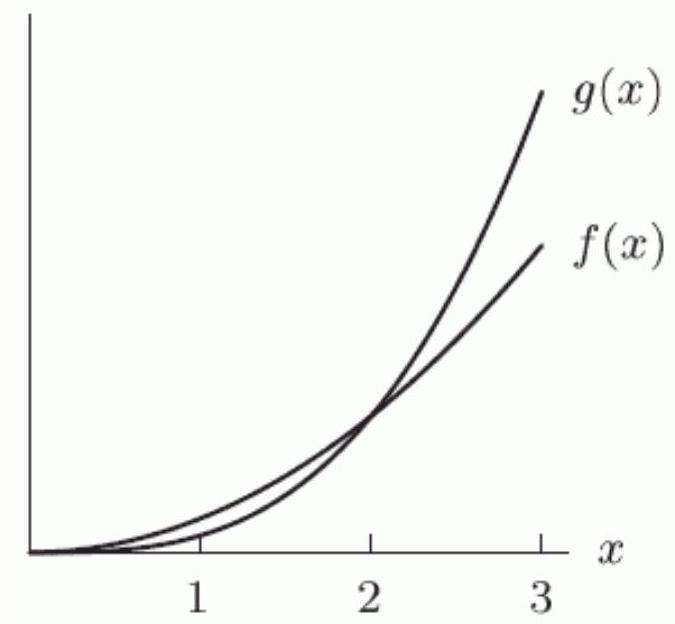
A) must be less than
B) might be less than
C) cannot be less than

A) must be less than
B) might be less than
C) cannot be less than

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
18
Find a power function through the two points and .

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
19
Is the function a power function? If so, write the function in the form .

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
20
Which of the following are true?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
21
The functions and are given by and .
Suppose . What must be?
Suppose . What must be?

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
22
The functions and are given by and .
Suppose . What must be?
A)
B)
C)
D)
Suppose . What must be?
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
23
Let . Which of the following statements are true?
A) As
B) As
C) As
D) As
A) As
B) As
C) As
D) As

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
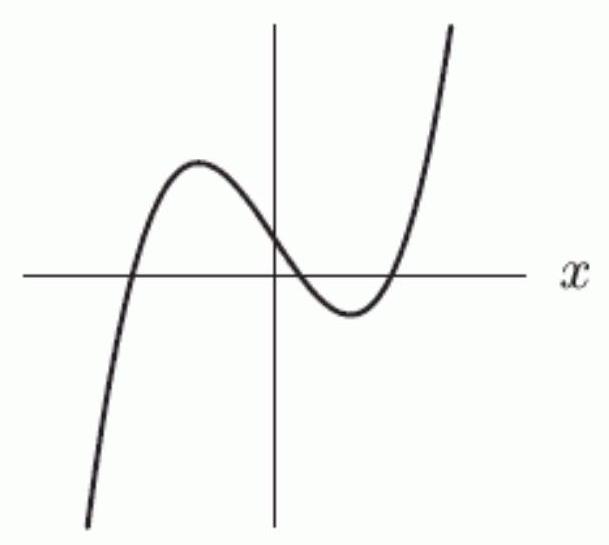
24
Let . If is a polynomial, give its degree. If not, enter "not a polynomial".

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
25
The polynomial graphed below has leading term (i.e. terms of lower degree). We know that is ----------- (positive \ negative), is ------------- (even \ odd), and the smallest possible value of is ----------------------.


Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
26
Let . Which of the following is the graph of ?
A)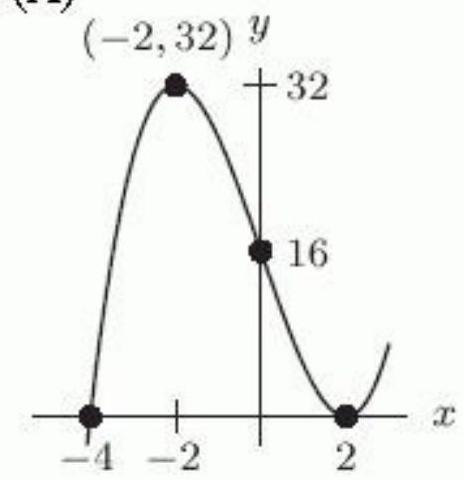
B)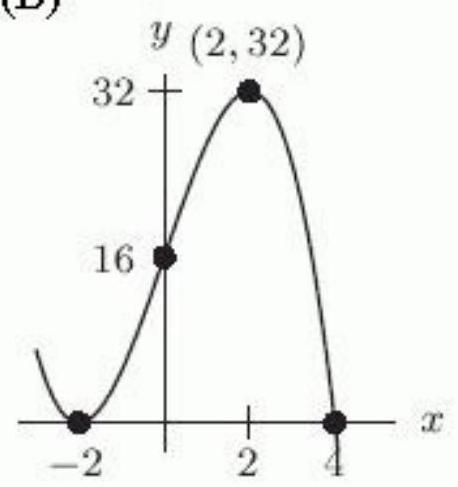
C)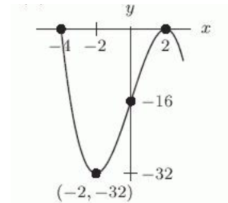
D)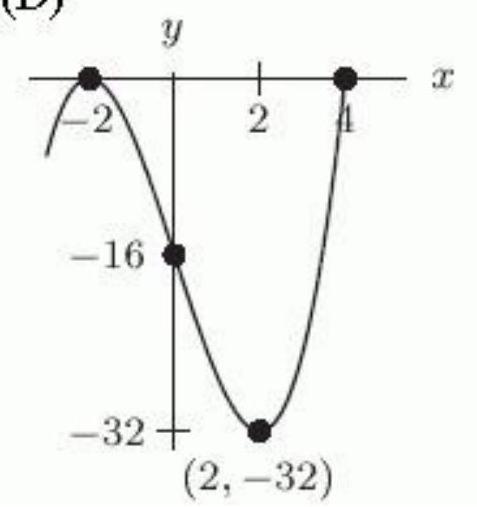
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
27
Let . The following figure shows the graph of , with ------------
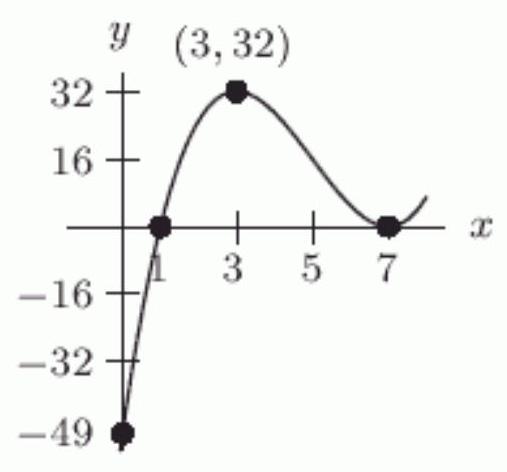


Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
28
Let . Which of the following figures shows the graph of ?
A)
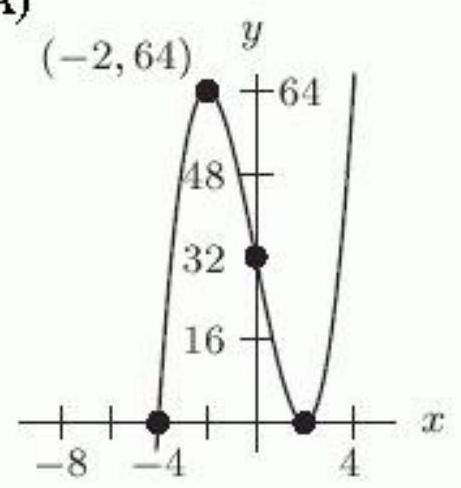
B)
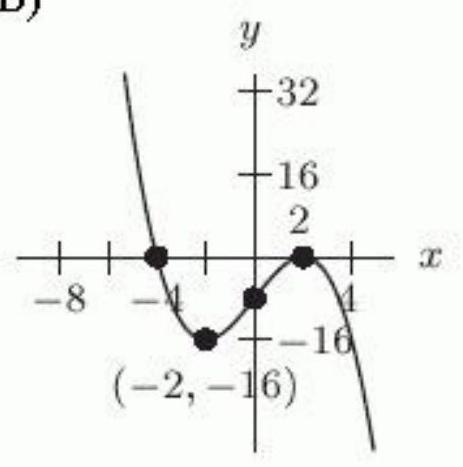
C)
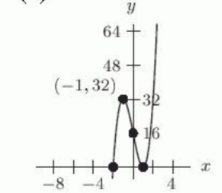
D)
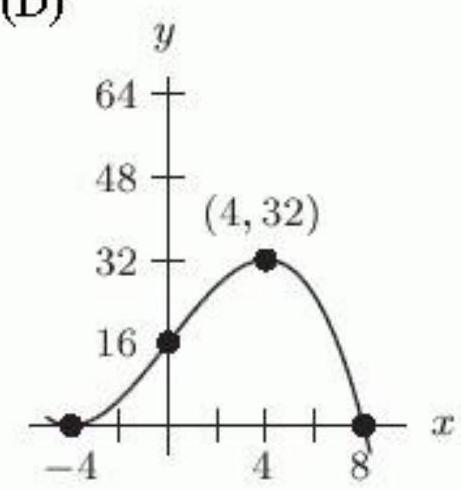
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
29
The volume of pollutants (in millions of cubic feet) in a certain reservoir is given by , where is time in years. The volume of the reservoir (including pollutants) is gradually increasing and is given by . Let be the fraction of the reservoir's volume that consists of pollutants. What percent of the reservoir's total volume consisted of pollutants in the year ? Round to 1 decimal place.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
30
The volume of pollutants (in millions of cubic feet) in a certain reservoir is given by , where is time in years. The volume of the reservoir (including pollutants) is gradually increasing and is given by . Let be the fraction of the reservoir's volume that consists of pollutants. If these trends continue for many years, approximately what percent of the reservoir's total volume would eventually be pollutants? Round to 1 decimal place.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
31
A sample of a certain alloy (mixture of metals) contains of tin and of copper. A chemist decides to study the properties of the alloy as its percentage of tin is varied. Suppose represents the quantity of tin, in , the chemist adds to the sample. Let represent the fraction of the mixture's mass composed of tin--that is, the ratio of the tin's mass to the mixture's total mass. A negative value of represents a quantity of tin removed from the original sample. What is the domain of ?
A) All real numbers .
B) All .
C) All .
D) All .
E) All .
A) All real numbers .
B) All .
C) All .
D) All .
E) All .

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
32
A sample of a certain alloy (mixture of metals) contains of tin and of copper. A chemist decides to study the properties of the alloy as its percentage of tin is varied. Suppose represents the quantity of tin, in , the chemist adds to the sample. Let represent the fraction of the mixture's mass composed of tin--that is, the ratio of the tin's mass to the mixture's total mass. A negative value of represents a quantity of tin removed from the original sample. There is a zero at ---------

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
33
The ant population in a sandbox has been modelled by the following function: where is the number of months after January 2010 .
a) How many ants are in the sandbox in January 2010 ?
b) How many ants are predicted to be in the sandbox in February 2011 ?
a) How many ants are in the sandbox in January 2010 ?
b) How many ants are predicted to be in the sandbox in February 2011 ?

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
34
Find the equation of the vertical line through the -intercept of the graph .

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
35
Find the equation of the horizontal line through the -intercept of the graph .

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
36
The sum of two even functions is always an odd function.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
37
Which of the following are polynomials:
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
38
Compute the following limits:
a)
b)
a)
b)

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
39
Compute the following limits:
a)
b)
a)
b)

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
40
Suppose that . Select all that are true:
A) is an odd function.
B) The -intercept of is 14
C) As then
D) As then
A) is an odd function.
B) The -intercept of is 14
C) As then
D) As then

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
41
What is the degree of the polynomial function ?

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
42
Does the function have a minimum value?

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
43
List the zeros of the function in ascending order, separated by commas.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
44
Use a graphing calculator or computer to graph . Use the graph to pick the factored form of .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
45
Describe the graph of .
A) A polynomial curve that goes down on the left and up on the right, has zeros at 4,2 , and -2 , and has a -intercept at -8 .
B) A polynomial curve that goes up on the left and down on the right, has zeros at 4, 2 , and -2 , and has a -intercept at -8 .
C) A polynomial curve that goes down on the left and up on the right, has zeros at , and 2 , and has a -intercept at -8 .
D) A polynomial curve that goes up on the left and down on the right, has zeros at , and 2 , and has a -intercept at -8 .
A) A polynomial curve that goes down on the left and up on the right, has zeros at 4,2 , and -2 , and has a -intercept at -8 .
B) A polynomial curve that goes up on the left and down on the right, has zeros at 4, 2 , and -2 , and has a -intercept at -8 .
C) A polynomial curve that goes down on the left and up on the right, has zeros at , and 2 , and has a -intercept at -8 .
D) A polynomial curve that goes up on the left and down on the right, has zeros at , and 2 , and has a -intercept at -8 .

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
46
Use a graphing calculator to find all the real zeros of . List them in ascending order, separated by commas.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
47
The graphs of and are shown in the figure below as viewed on the window by . What is the double zero of ?
![The graphs of y_{1}=0.25 x^{4} and y_{2}=0.25\left(x^{4}+x^{3}-23 x^{2}+3 x+90\right) are shown in the figure below as viewed on the window [-10,10] by [-25,25] . What is the double zero of y_{2} ?](https://storage.examlex.com/TBW1046/11eebd06_93d7_5429_9a32_8b4be43b7b04_TBW1046_00.jpg)
![The graphs of y_{1}=0.25 x^{4} and y_{2}=0.25\left(x^{4}+x^{3}-23 x^{2}+3 x+90\right) are shown in the figure below as viewed on the window [-10,10] by [-25,25] . What is the double zero of y_{2} ?](https://storage.examlex.com/TBW1046/11eebd06_93d7_5429_9a32_8b4be43b7b04_TBW1046_00.jpg)

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
48
The graphs of and are shown in the figure below as viewed on the window by . What happens as the viewing window is expanded?
![<strong>The graphs of y_{1}=0.25 x^{4} and y_{2}=0.25\left(x^{4}+x^{3}-23 x^{2}+3 x+90\right) are shown in the figure below as viewed on the window [-10,10] by [-25,25] . What happens as the viewing window is expanded? </strong> A) The graphs become further apart from each other. B) The graphs become indistinguishable from one another. C) Nothing changes.](https://storage.examlex.com/TBW1046/11eebd06_93d7_542a_9a32_1b2b3032adc3_TBW1046_00.jpg)
A) The graphs become further apart from each other.
B) The graphs become indistinguishable from one another.
C) Nothing changes.
![<strong>The graphs of y_{1}=0.25 x^{4} and y_{2}=0.25\left(x^{4}+x^{3}-23 x^{2}+3 x+90\right) are shown in the figure below as viewed on the window [-10,10] by [-25,25] . What happens as the viewing window is expanded? </strong> A) The graphs become further apart from each other. B) The graphs become indistinguishable from one another. C) Nothing changes.](https://storage.examlex.com/TBW1046/11eebd06_93d7_542a_9a32_1b2b3032adc3_TBW1046_00.jpg)
A) The graphs become further apart from each other.
B) The graphs become indistinguishable from one another.
C) Nothing changes.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
49
If and , then on the interval ----------- (

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
50
The function can be approximated by the function . On what interval do the two graphs look similar?
A)
B)
C)
A)
B)
C)

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
51
What are the zeros of ? List them in ascending order separated by commas, and round any non-integer zeros to 3 decimal places.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
52
The formula for the function graphed below has leading term (i.e. terms of lower degree). If is as small as possible, then ---------- and a= ----------
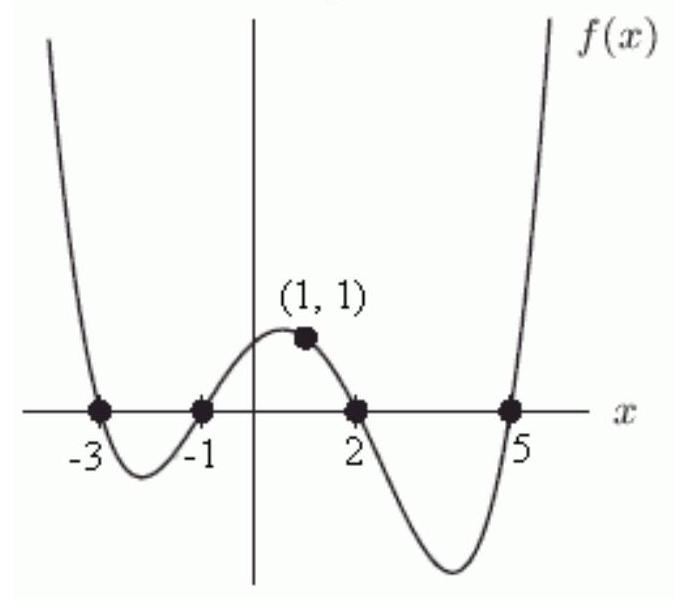


Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
53
Which of the following could represent a complete graph of where is a constant?
A)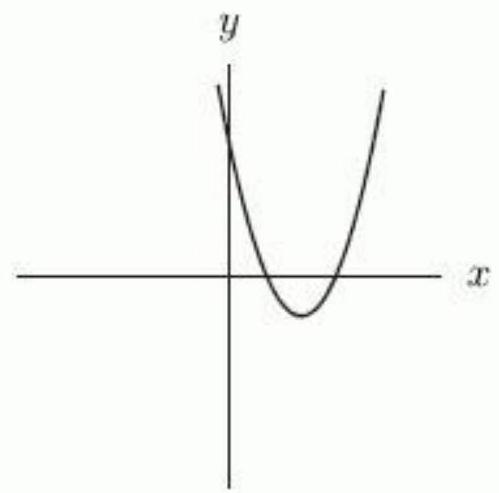
B)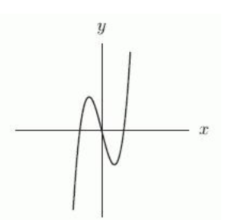
C)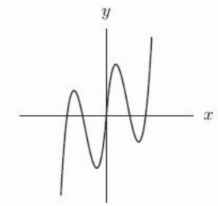
D)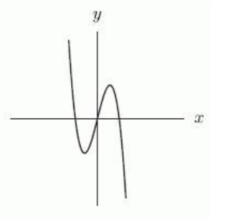
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
54
A polynomial with integer coefficients having as a zero is , where , and . Make your value for be positive and as small as possible.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
55
Which of the following could be a formula for the graph shown below?
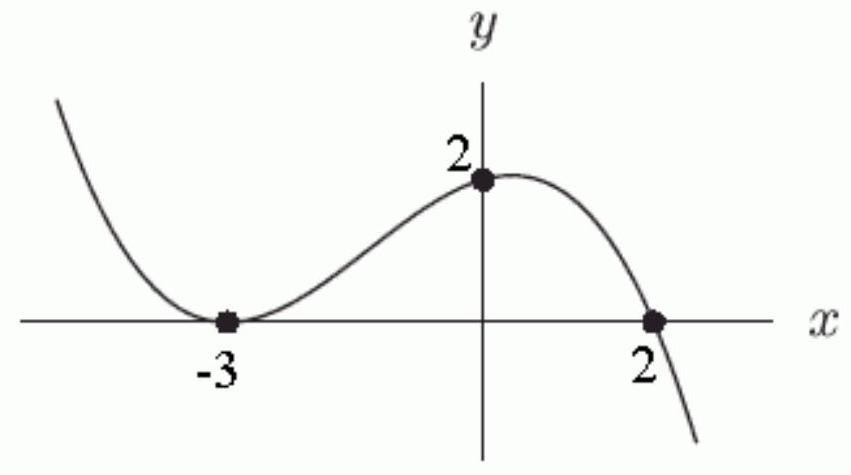
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
56
Farmer Brown has 115 feet of fence. He wishes to close in a rectangular field using the barn as one side of the field. Suppose each side of the field perpendicular to the barn has length feet. What is the area of the fenced in field?
A) The area of the field is square feet.
B) The area of the field is square feet.
C) The area of the field is square feet.
D) The area of the field is square feet.
A) The area of the field is square feet.
B) The area of the field is square feet.
C) The area of the field is square feet.
D) The area of the field is square feet.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
57
Farmer Brown has 112 feet of fence. He wishes to close in a rectangular field using the barn as one side of the field. Suppose each side of the field perpendicular to the barn has length feet.
a) What is the area of the fenced in field in terms of ?
b) In the context of this problem, what values of make sense?
c) Approximate the maximum volume of the fenced field.
a) What is the area of the fenced in field in terms of ?
b) In the context of this problem, what values of make sense?
c) Approximate the maximum volume of the fenced field.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
58
A right circular cylinder has a volume of 122 cubic meters.
a) What is the formula for surface area in terms of the radius, , of the base of the cylinder?
b) Approximate the least possible surface area for the cylinder.
c) Approximate the radius necessary to achieve the minimum surface area.
Round answers to 3 decimal places if necessary.
a) What is the formula for surface area in terms of the radius, , of the base of the cylinder?
b) Approximate the least possible surface area for the cylinder.
c) Approximate the radius necessary to achieve the minimum surface area.
Round answers to 3 decimal places if necessary.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
59
A right circular cylinder has a volume of 128 cubic meters. The least possible surface area for the cylinder is approximately:
A) 140.6008 square meters.
B) 256 square meters.
C) 296.1061 square meters.
D) 128 square meters.
A) 140.6008 square meters.
B) 256 square meters.
C) 296.1061 square meters.
D) 128 square meters.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
60
The domain of the function is
A) all except for
B) all
C)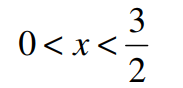
D) all
A) all except for
B) all
C)
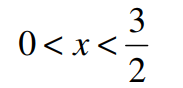
D) all

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
61
What is the domain of the function ?

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
62
Find the formula for a third degree polynomial with a zero at , a double zero at , and -intercept at -135 .

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
63
Which of the following are possible formulas for a fourth degree polynomial with at least one zero at , a double zero at , and long-run behavior: as . .
A)
B)
C)
D) where
A)
B)
C)
D) where

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
64
What is the domain of the function ?

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
65
Let . As from the right, -------- .Enter "infinity" for and "-infinity" for .

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
66
Let . As . Enter "infinity" for and
"-infinity" for .
"-infinity" for .

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
67
Does the figure below show an accurate graph of ?
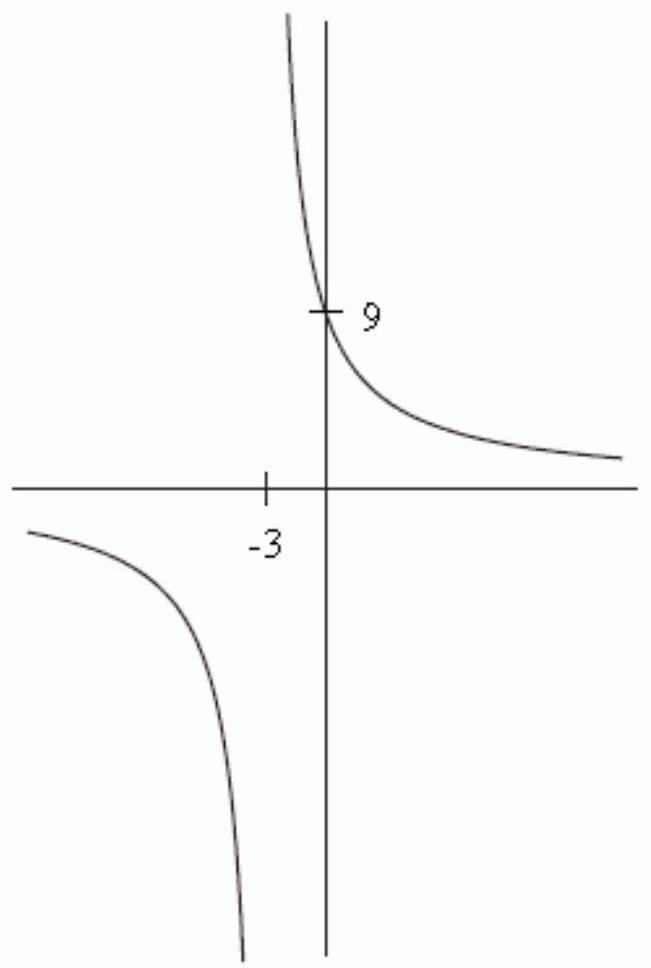


Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
68
Is a rational function?

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
69
If the function is written in the form , a ratio of polynomials, which of the following could be ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
70
If the function is written in the form , a ratio of polynomials, which of the following could be ?
A)
B)
C)
D) -8
A)
B)
C)
D) -8

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
71
The horizontal asymptote of is . Enter "none" if there is no horizontal asymptote.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
72
The following figure gives the graphs of four power functions. Which one could be the graph of ? If none of the graphs match, enter "none".
A)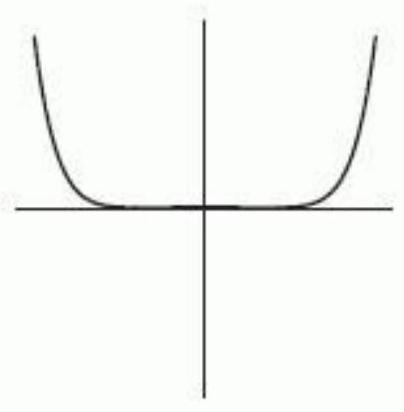
B)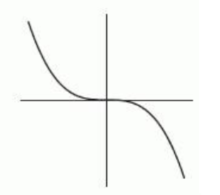
C)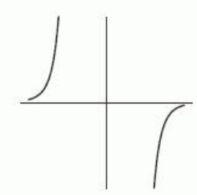
D)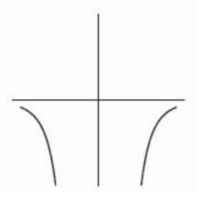
E) none
A)

B)

C)

D)

E) none

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
73
The following figure gives the graphs of four power functions. Which one could be the graph of ? If none of the graphs match, enter "none".
A)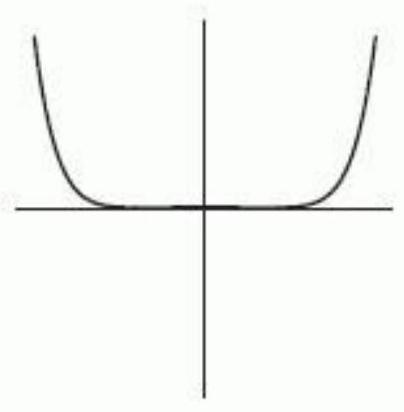
B)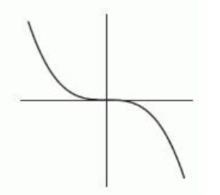
C)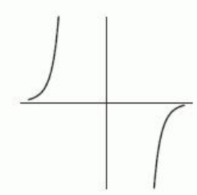
D)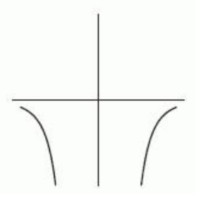
E) none
A)

B)

C)

D)

E) none

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
74
Must the sum of two functions with horizontal asymptotes also have a horizontal asymptote?

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
75
A sample of a certain alloy (mixture of metals) contains of tin and of copper. A chemist decides to study the properties of the alloy as its percentage of tin is varied. Suppose represents the quantity of tin, in , the chemist adds to the sample. Let represent the fraction of the mixture's mass composed of tin--that is, the ratio of the tin's mass to the mixture's total mass. A negative value of represents a quantity of tin removed from the original sample. f(0.6)= ----------- (kg tin) (kg mixture) Round to 2 decimal places.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
76
A sample of a certain alloy (mixture of metals) contains of tin and of copper. A chemist decides to study the properties of the alloy as its percentage of tin is varied. Suppose represents the quantity of tin, in , the chemist adds to the sample. Let represent the fraction of the mixture's mass composed of tin--that is, the ratio of the tin's mass to the mixture's total mass. A negative value of represents a quantity of tin removed from the original sample. ------------ kg. Round to 2 decimal places.

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
77
The infant mortality, , in a country is related to the country's GNP (gross national product), . Some authors (Weld and Helms, 1971) have argued that the relationship is of the form , where , and are positive constants and . For , and , the vertical asymptote of the graph of against is at ------------ If there is no vertical asymptote, enter "none"

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
78
Suppose that is a power function and that . Must ?

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
79
Which of the following are rational functions:
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck
80
Let . Find .

Unlock Deck
Unlock for access to all 145 flashcards in this deck.
Unlock Deck
k this deck


