Deck 12: Vectors and Matrices
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/104
Play
Full screen (f)
Deck 12: Vectors and Matrices
1
Is the distance between a satellite and the earth a vector or a scalar?
scalar
2
Which of the following would be described by vectors rather than scalars?
A) The number of lions at the zoo.
B) The number of dogs and frogs at the pet store.
C) The velocity of a hot air balloon.
D) The height of your math teacher.
A) The number of lions at the zoo.
B) The number of dogs and frogs at the pet store.
C) The velocity of a hot air balloon.
D) The height of your math teacher.
The velocity of a hot air balloon.
The height of your math teacher.
The height of your math teacher.
3
A kite on a 26 meter string is flying with an angle of with the ground. What is the magnitude and the direction of the vector from the kite to the ground. Round numbers to 3 decimal places if necessary.
The vector points directly downward and has magnitude 14.161 meters
4
Simplify

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
5
Simplify

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
6
Suppose a man starts at work and drives due south, and then drives southeast. How far is the man from work? Round numbers to 3 decimal places if necessary.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
7
A canoe can travel in still water. Suppose a river is flowing at a rate of 5 . If the canoe is traveling downstream at an angle of with the current, what is the speed of the canoe? Round numbers to 3 decimal places if necessary.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
8
A man leaves his car and walks 2 miles northeast, 4 miles east, and then 8 miles southwest. How far is the person from his car? In what direction must he walk to head directly to his car? Round numbers to 3 decimal places if necessary.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
9
A man is sitting 9 meters above the ground in a tree which is 10 meters directly south of the fence corner of a field. A bird is spotted 2 meters above the ground and 8 meters directly north of the fence corner. How far is the man from the bird? Round your answer to 3 decimal places.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
10
A man is sitting 8 meters above the ground in a tree which is 10 meters directly south of the fence corner of a field. A bird is spotted 3 meters above the ground and 9 meters directly north of the fence corner. In what direction must the man face to look directly at the bird? Round your answer to 3 decimal places.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
11
A horse runs at a constant speed of . He starts at a fence and his path makes an angle of with the fence. After 9 seconds, how far is he from the fence? Round numbers to 3 decimal places if necessary.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
12
What properties of vector addition and scalar multiplication are necessary to show

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
13
Does point in the same direction as , the opposite direction, or neither?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
14
Let be a vector of length 3 pointing north of east. Find the length and direction of .

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
15
Let be a vector of length 3 pointing north of east. Find the length and direction of .

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
16
Jack and Jill begin walking away from a water well. Jill walks 2 meters north, and then 12 meters east. When Jill stops, Jack is twice as far from the well as she is. How far is Jack from the well? Round numbers to 3 decimal places if necessary.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
17
Jack and Jill begin walking away from a water well. Jill walks 3 meters north, and then 14 meters northeast. When Jill stops, Jack is half as far from the well as she is. How far is Jack from the well? Round numbers to 3 decimal places if necessary.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
18
Jack and Jill begin walking away from a water well. Jill walks 4 meters west, and then 2 meters north. When Jill stops, Jack is three times as far from the well as she is, but in the opposite direction. If is the vector pointing from Jack to the well, find the length and direction of . Round numbers to 3 decimal places if necessary.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
19
Simplify the following:

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
20
Simplify the following:

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
21
The figure below shows the vector ---------- ---------- .
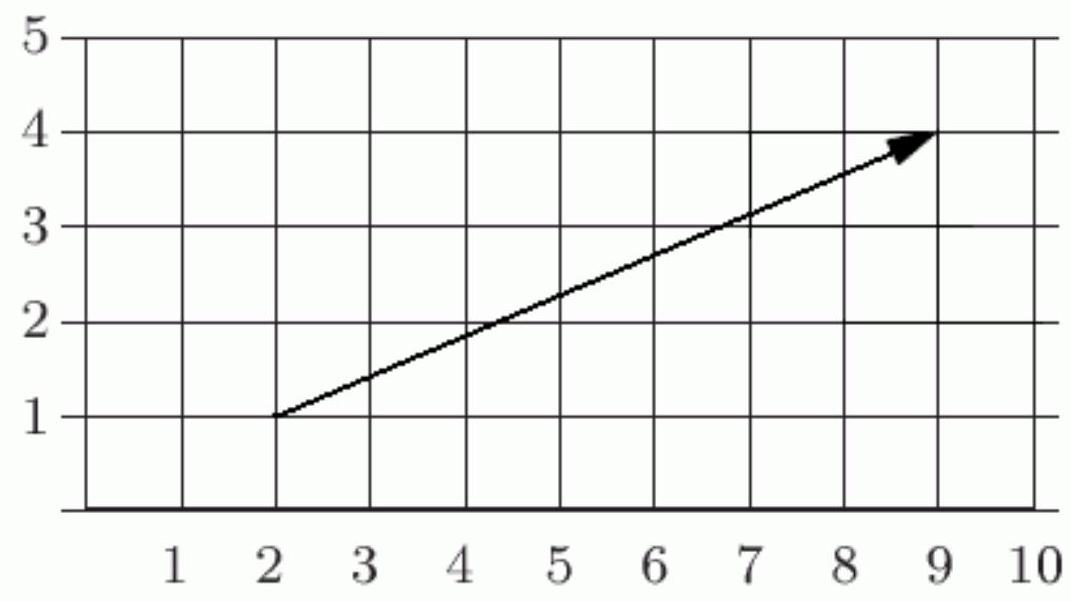


Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
22
The vector starting at the point and ending at the point can be resolved into the components ----------------- --------------

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
23
Find the length of the vector to 3 decimal places.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
24
A boat in the ocean at point is looking at the light on a lighthouse at point . The light house is 3 units high, and sits at the edge of a cliff above the ocean. The displacement vector between the boat and the base of the lighthouse is ------------- ---------- ---------- .

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
25
A car travels 19 miles south and then 23 miles east. Which of the following is true?
A) Its net displacement is 29.83 miles.
B) Its net displacement is 29.83 miles south of east.
C) Its net displacement is 42 miles.
D) Its net displacement is 42 miles south of east.
A) Its net displacement is 29.83 miles.
B) Its net displacement is 29.83 miles south of east.
C) Its net displacement is 42 miles.
D) Its net displacement is 42 miles south of east.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
26
Let the -axis point east, the -axis point north, and the -axis point upward, and let the unit vectors be in kilometers. What does the vector represent?
A) A displacement of east, followed by a displacement of north and a displacement of up.
B) A displacement of west, followed by a displacement of north and a displacement of up.
C) A displacement of east, followed by a displacement of south and a displacement of up.
D) A displacement of west, followed by a displacement of south and a displacement of up.
A) A displacement of east, followed by a displacement of north and a displacement of up.
B) A displacement of west, followed by a displacement of north and a displacement of up.
C) A displacement of east, followed by a displacement of south and a displacement of up.
D) A displacement of west, followed by a displacement of south and a displacement of up.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
27
For what value of do and have the same length?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
28
If , what is ?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
29
Find the length of the vector if and .

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
30
Let and . Write the displacement vector in component form.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
31
Let and . Write the displacement vector in component form.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
32
If . Find such that is parallel to .

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
33
Let and . Find a vector of length 9 pointing in the opposite direction of .

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
34
A cannon is fired at a angle with the ground at a speed of . Resolve the velocity vector into horizontal and vertical components.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
35
The vectors and are parallel.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
36
The vectors and are parallel.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
37
In the figure below, each square is 6 units along each side. In component form, ------------- ---------- .
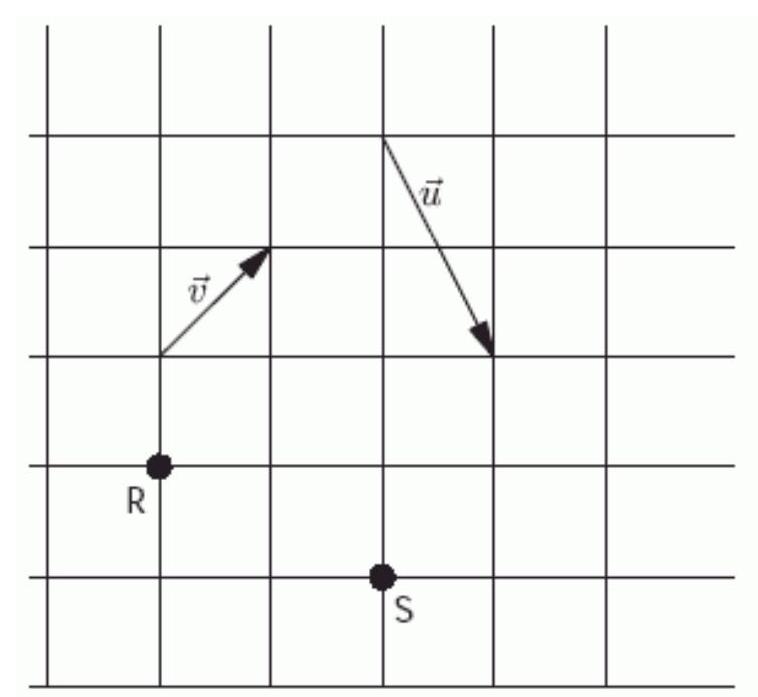


Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
38
In the figure below, each square is 9 units along each side. In component form, 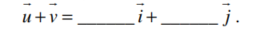
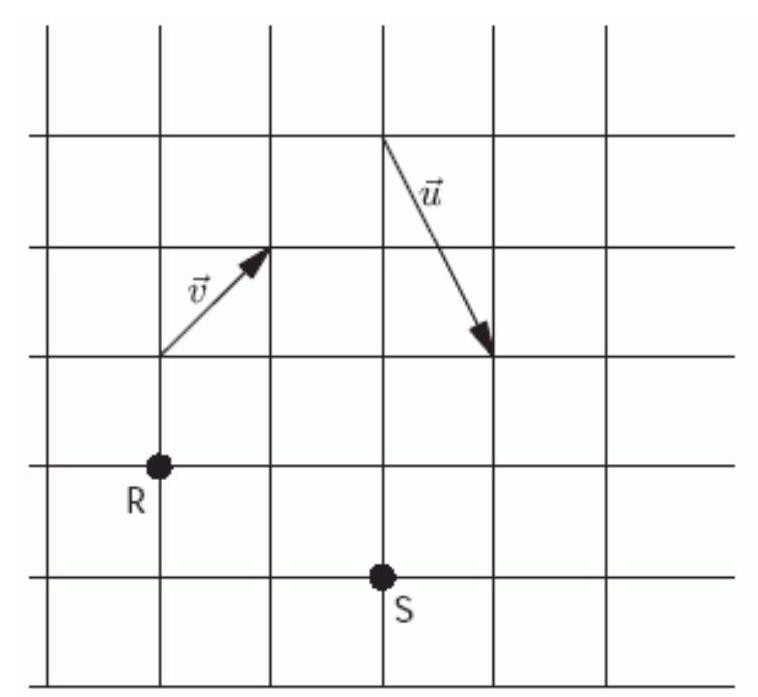
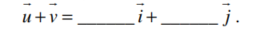


Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
39
In the figure below, each square is 7 units along each side. The vector perpendicular to the displacement vector is ----------- .
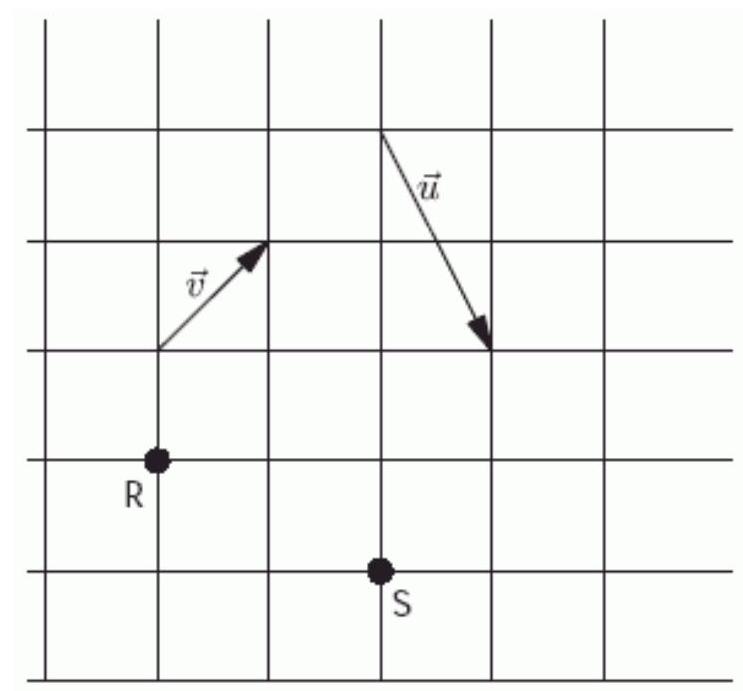


Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
40

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
41
Perform the computation .

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
42
Perform the computation .

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
43
A particle in equilibrium is acted upon by three forces, two of which have components and . The components of the third must be ------ .

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
44
As changes, what happens to the tip of the vector ?
A) It moves in a straight line parallel to the vector .
B) It moves in a straight line parallel to the vector .
C) It moves in a straight line parallel to the vector .
D) None of the above.
A) It moves in a straight line parallel to the vector .
B) It moves in a straight line parallel to the vector .
C) It moves in a straight line parallel to the vector .
D) None of the above.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
45
The unit vector from the point toward the point has its head at the point ( -------------,------------). Round to 2 decimal places.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
46
Let give the profit a salesman makes from selling three different models of computers. Let give the number of each computer model sold each week. What does represent?
A) A scalar giving the total profit for one week from selling all three models of computers.
B) A scalar giving the average profit for one week from selling each computer model.
C) A vector giving the profit for one week for the three models of computers.
D) A vector giving the average profit for one week for the three models of computers.
A) A scalar giving the total profit for one week from selling all three models of computers.
B) A scalar giving the average profit for one week from selling each computer model.
C) A vector giving the profit for one week for the three models of computers.
D) A vector giving the average profit for one week for the three models of computers.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
47
A retailer's total monthly sales of three different models of television is given by the vector . If the sales for each model go up by 7 the next month, what is , the next month's total sales?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
48
A retailer's total monthly sales of three different models of television is given by the vector . If the sales for each model go down by the next month, what is , the next month's total sales? Round entries to the nearest whole number.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
49
If and , then what is ?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
50
A snow cone stand sells three sizes of snow cones: small, medium, and large. Let give the number of each type of cone sold in one day. Let give the price (in dollars) charged for each size of snow cone, give the cost (also in dollars) of making each size of snow cone, and give the maximum number of each size that can be sold (because of the number of each size cup on hand.) What is the total number of cups left in the stand at the end of the day?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
51
A snow cone stand sells three sizes of snow cones: small, medium, and large. Let give the number of each type of cone sold in one day. Let give the price (in dollars) charged for each size of snow cone, give the cost (also in dollars) of making each size of snow cone, and give the maximum number of each size that can be sold (because of the number of each size cup on hand). How much money was spent making the medium snow cones that day?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
52
If and , then what is ?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
53
If and , find .

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
54
There are six people taking a vocational exam with both oral and written parts. Their scores (out of 100) on the written section are given by the vector . Their scores (out of 100) on the oral section are given by the vector . Find the vector giving their composite score if the written part counts twice as much as the oral part.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
55
If and , find

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
56
An airplane flies at an airspeed of in a cross-wind that is blowing from the southwest at a speed of . What direction should the plane fly to end up going due south?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
57
The rectangle with vertices , and is rotated through an angle of about the origin. What are the coordinates of the new rectangle? Round numbers to 3 decimal places if necessary.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
58
Let the student vector be the number of ninth, tenth, eleventh, and twelfth graders in a high school. If the number of students in each grade increases by , what is the new student vector ? Round to the nearest whole number.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
59
Let and .
Find
Find

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
60
Let and .
Find .
Find .

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
61
Let the student vector be the number of ninth, tenth, eleventh, and twelfth graders in a high school. If the number of students in each grade increases by 5 , what is the new student vector ?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
62
Let the student vector be the number of ninth, tenth, eleventh, and twelfth graders in a high school. If the number of students in each grade doubles, what is the new student vector ?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
63
Given the vector find vector .

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
64
A particle is acted on by two forces, one of them to the west and of magnitude 0.5 dynes (a dyne is a unit of force), and the other in the direction north of east and of magnitude 1 dyne. A third force acting upon the particle that would keep it at equilibrium has a magnitude of ------- dynes and points ------------(north \ south \ east \ west). Round the first answer to 2 decimal places.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
65
A cyclist goes at 6 mph due north and feels the wind coming against him at a relative velocity of 3 mph due west. The actual velocity of the wind is ----------mph at an angle of ---------------°west of north. Round both answers to 1 decimal place.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
66
A gun mounted on a train points vertically upward. The train moves horizontally due east at 80 mph and the gun fires a bullet with a muzzle velocity of 80 mph. The speed and direction of the bullet relative to the ground is ------------ mph toward the east at ------------° to the horizontal. Round the first answer to 2 decimal places.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
67
For and , what is ?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
68
For and , .

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
69
For and , what is ?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
70
A model pyramid is built using four equilateral triangles connected to a square base. If the length of one side of the base is 11 inches, how many inches high is the pyramid? Round to 2 decimal places.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
71
A vector of length 7 that points in the same direction as is . Give each answer to 3 decimal places.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
72
For what value of are and parallel?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
73
In the figure below, the angle between the -axis and the vector is------------° Round to the nearest whole number.
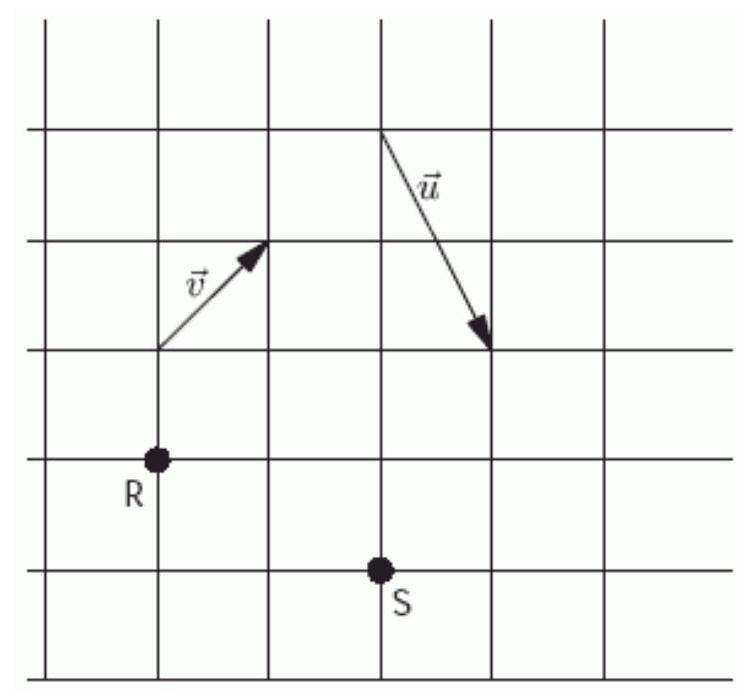


Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
74
An airplane is flying at an airspeed of 620 km/hr in a crosswind blowing from the southeast at a speed of 55 km/hr. To end up going due east, the plane should head ---------°south of east and will have a speed of ---------- km/hr relative to the ground. Round each answer to 2 decimal places.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
75
Let the vector describe a triangle with vertices at , , and . If the triangle is rotated through an angle of clockwise about the origin, what is the resulting vector? Round each entry to 2 decimal places.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
76
Three people stand in the middle of a field. The first person walks 15 yards north and then 15 yards east. The second person remains where he is. The third person walks 20 yards north and then 9 yards east. The angle formed by drawing a line from the first person to the second person to the third person is ----------°. Round to the nearest whole number.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
77
How many ft-lbs of work are required to lift a 371 pound refrigerator 3 inches straight up? Round to 2 decimal places.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
78
The angle between the vectors and is---------. Round to the nearest whole number.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
79
Do the points , and form a square?

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck
80
An airplane is flying at an airspeed of 600 km/hr in a crosswind blowing from the southeast at a speed of 50 km/hr. To end up going due west, the plane should head ------------° south of west and will have a speed of ----------- km/hr relative to the ground. Round each answer to 2 decimal places.

Unlock Deck
Unlock for access to all 104 flashcards in this deck.
Unlock Deck
k this deck


