Deck 14: Parametric Equations and Conic Sections
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/128
Play
Full screen (f)
Deck 14: Parametric Equations and Conic Sections
1
Describe the graph of the parametric equations for 0.
A) A circle of radius 2, centered at the origin and traced in the clockwise direction.
B) The right half of a circle of radius 2, centered at the origin, traced in the clockwise direction, and never quite reaching the point .
C) The lower half of a circle of radius 2 , centered at the origin, traced in the counterclockwise direction, and never quite reaching the point .
D) The upper half of a circle of radius 2, centered at the origin, traced in the clockwise direction, and never quite reaching the point .
A) A circle of radius 2, centered at the origin and traced in the clockwise direction.
B) The right half of a circle of radius 2, centered at the origin, traced in the clockwise direction, and never quite reaching the point .
C) The lower half of a circle of radius 2 , centered at the origin, traced in the counterclockwise direction, and never quite reaching the point .
D) The upper half of a circle of radius 2, centered at the origin, traced in the clockwise direction, and never quite reaching the point .
The upper half of a circle of radius 2, centered at the origin, traced in the clockwise direction, and never quite reaching the point .
2
Let be one part of a parametric equation. Which of the following formulas for as a function of on completes the parameterization of the graph of a straight line from to , and then continuing from in a straight line to ?
A)
B)
C)
D)
A)
B)
C)
D)
3
Could the graph below be the graph of the parametric equations ? Assume the parameter is restricted to values for which the functions are defined.
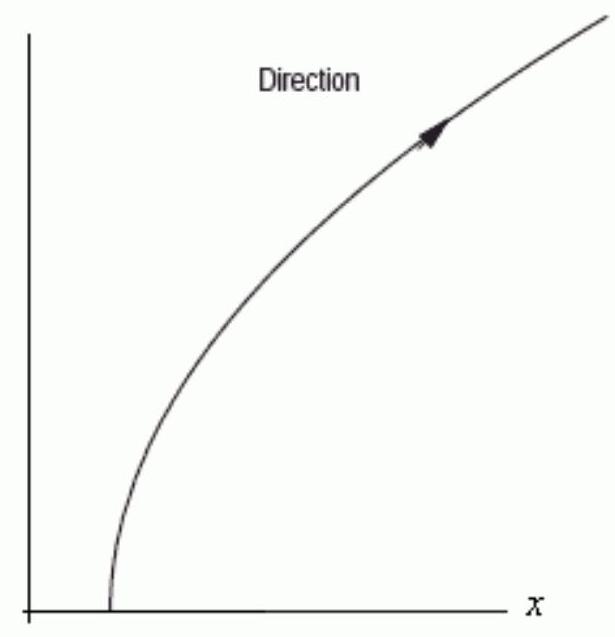

False
4
Could the graph below be the graph of the parametric equations ? Assume the parameter is restricted to values for which the functions are defined.
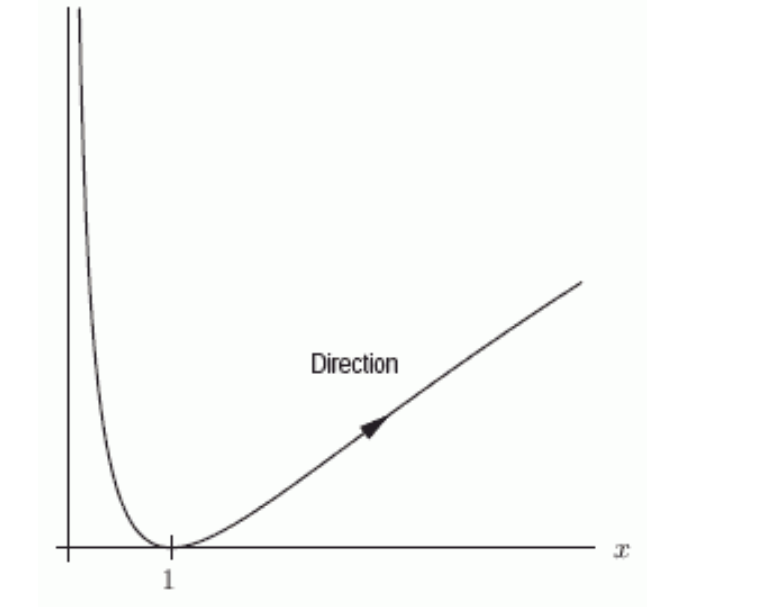


Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
5
Could the graph below be the graph of the parametric equations ? Assume the parameter is restricted to values for which the functions are defined.
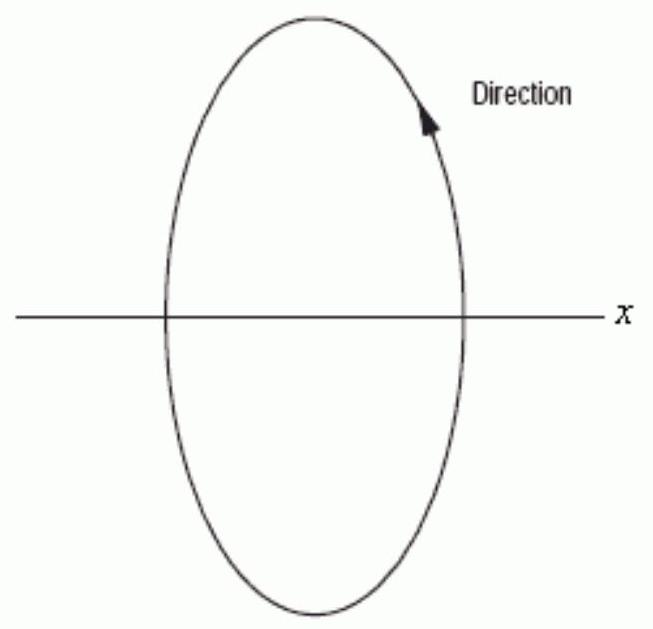


Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
6
What is the explicit formula for the curve ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
7
Describe the graph of the curve .
A) The graph looks like the graph of translated 6 units to the right and 7 units up.
B) The graph looks like the graph of translated 7 units to the right and 6 units up
C) The graph looks like the graph of translated 6 units to the right and 7 units up.
D) The graph looks like the graph of translated 7 units to the right and 6 units up.
A) The graph looks like the graph of translated 6 units to the right and 7 units up.
B) The graph looks like the graph of translated 7 units to the right and 6 units up
C) The graph looks like the graph of translated 6 units to the right and 7 units up.
D) The graph looks like the graph of translated 7 units to the right and 6 units up.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
8
What is the explicit formula for the curve ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
9
Describe the graph of the parametric equations .
A) The parabola .
B) The right half of the parabola .
C) The circle .
D) The top half of the circle .
A) The parabola .
B) The right half of the parabola .
C) The circle .
D) The top half of the circle .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
10
Is the equation explicit or implicit?

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
11
What are the endpoints for the curve ? Mark both correct answers.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
12
Give a parameterization for the straight line segment joining the points and .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
13
Give a parameterization for the upper half circle of radius 3 centered at , and starting at

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
14
Give a parameterization for the vertical line through the point .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
15
Give a parameterization for the horizontal line through the point .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
16
The line between and can be parameterized by , .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
17
The line between and can be parametrized by , .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
18
As varies, the equations and trace out a circle.
a) Describe the center and radius of the circle.
b) If , what part of the circle is obtained?
a) Describe the center and radius of the circle.
b) If , what part of the circle is obtained?

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
19
Let .
a) Graph the curve.
b) Eliminate the parameter to obtain an equation for as a function of .
a) Graph the curve.
b) Eliminate the parameter to obtain an equation for as a function of .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
20
Let .
a) Graph the curve.
b) Eliminate the parameter to obtain an equation for as a function of .
a) Graph the curve.
b) Eliminate the parameter to obtain an equation for as a function of .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
21
Choose the parametric equations that describe the curve
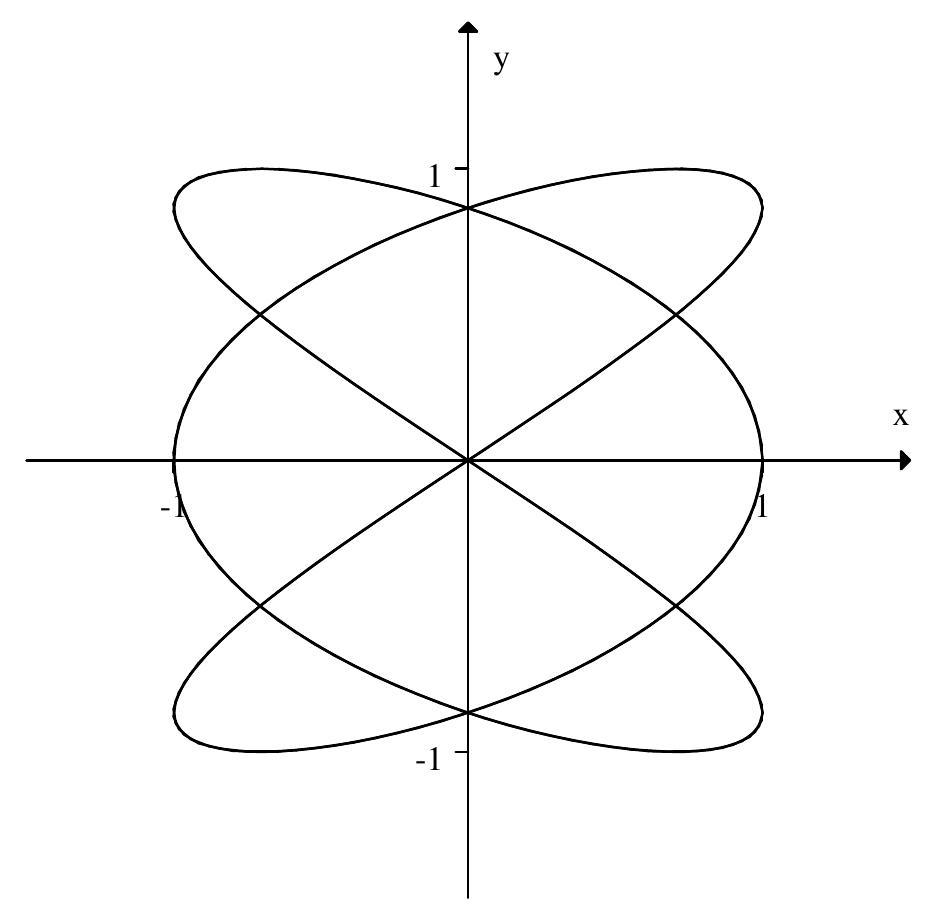
A) and
B) and
C) and
D) and

A) and
B) and
C) and
D) and

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
22
Choose the parametric equations that describe the curve
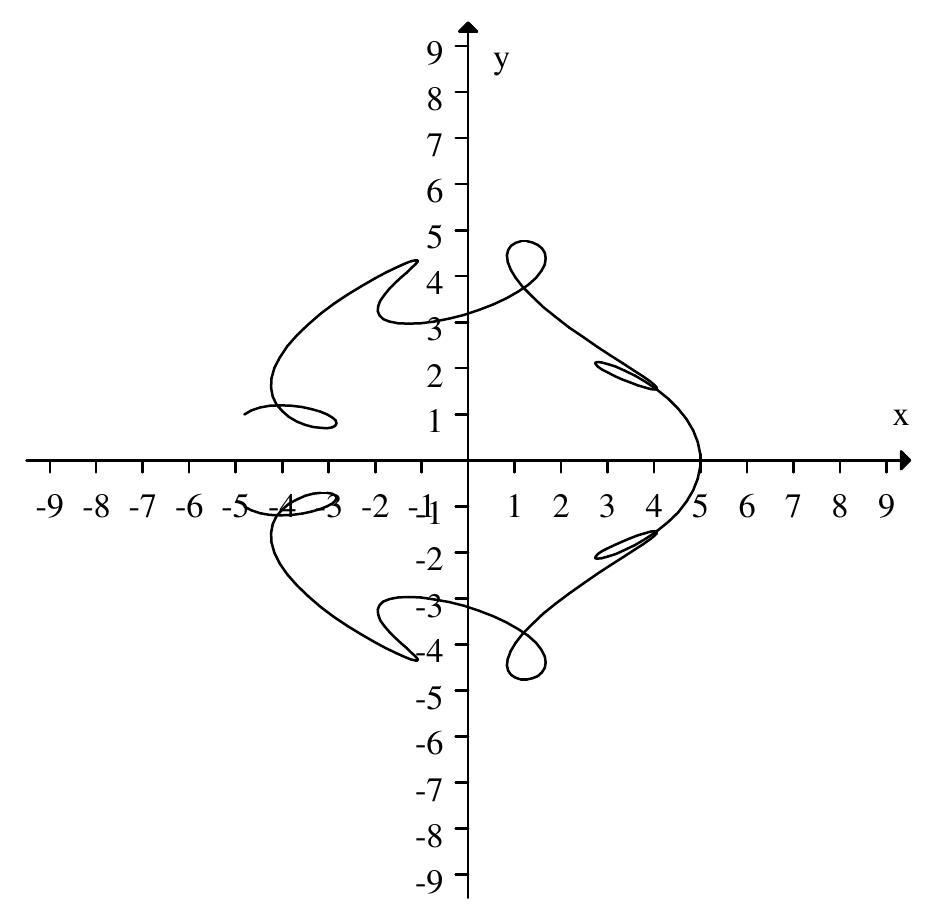
A) and
B) and
C) and
D) and

A) and
B) and
C) and
D) and

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
23
A mouse hanging on to the end of the windmill blade shown below has coordinates given by , where the origin is at the center of the blades, and are in meters, and is in seconds. The blades are 6 meters long and the windmill makes one complete revolution every 20 seconds in a counterclockwise direction. The mouse starts in the 3 o'clock position and, 7.5 seconds later, loses its hold and flies off. What is ?
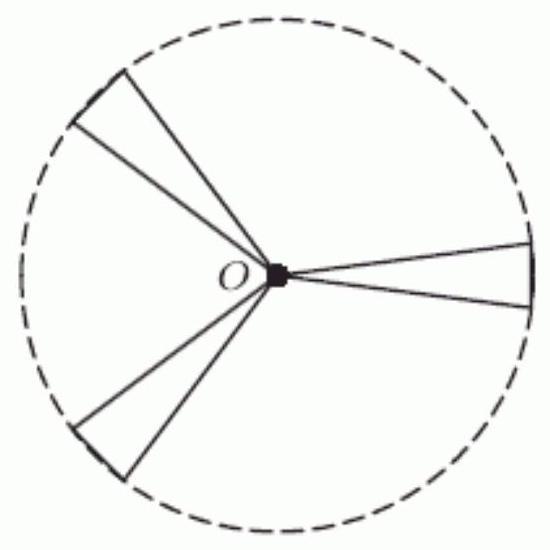


Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
24
A mouse hanging on to the end of the windmill blade shown below has coordinates given by , where the origin is at the center of the blades, and are in meters, and is in seconds. The blades are 7 meters long and the windmill makes one complete revolution every 32 seconds in a counterclockwise direction. The mouse starts in the 3 o'clock position and, 4 seconds later, loses its hold and flies off. What is ? Round to 2 decimal places.
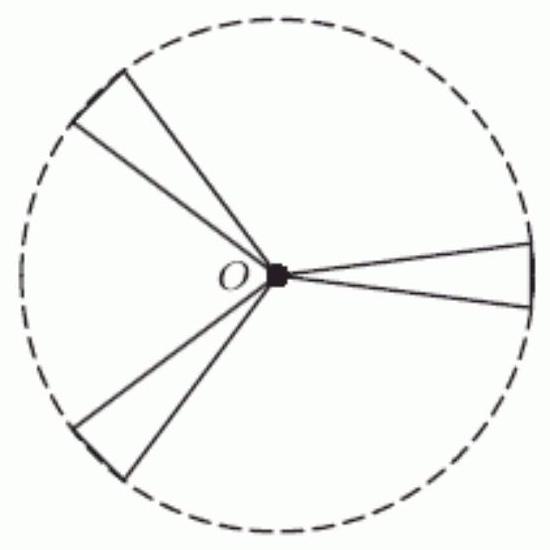


Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
25
A mouse hanging on to the end of the windmill blade shown below has coordinates given by , where the origin is at the center of the blades, and are in meters, and is in seconds. The blades are 3 meters long and the windmill makes one complete revolution every 20 seconds in a counterclockwise direction. The mouse starts in the 3 o'clock position and, 7.5 seconds later, loses its hold and flies off. How many meters\sec. is the mouse traveling while it is on the blade? Round to 2 decimal places.
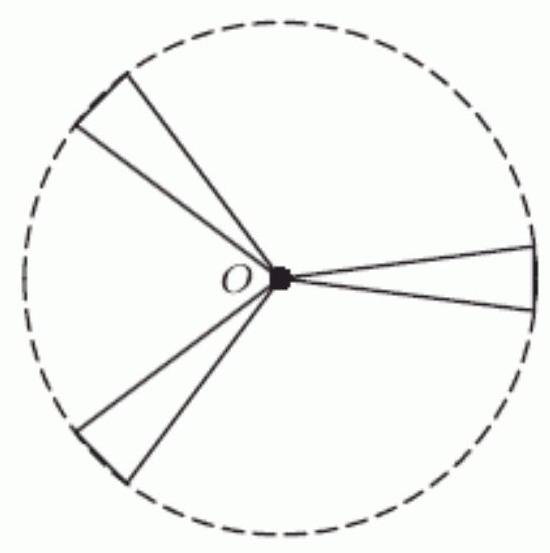


Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
26
A mouse hanging on to the end of the windmill blade shown below has coordinates given by , where the origin is at the center of the blades, and are in meters, and is in seconds. The blades are 5 meters long and the windmill makes one complete revolution every 28 seconds in a counterclockwise direction. The mouse starts in the 3 o'clock position and, 3.5 seconds later, loses its hold and flies off. How many degrees is the angle between the blade and the positive -axis at the moment the mouse flies off?
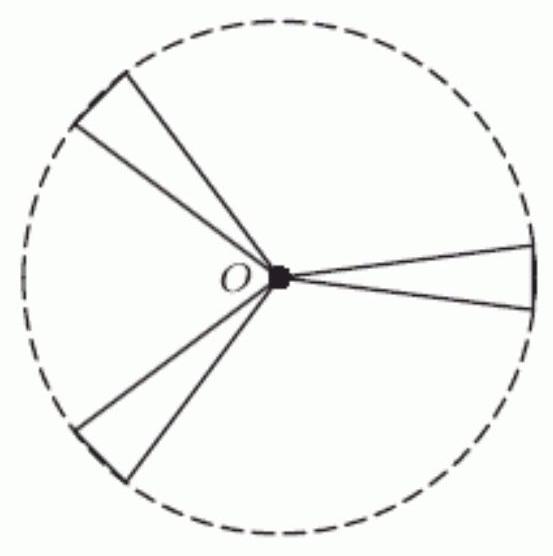


Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
27
A mouse hanging on to the end of the windmill blade shown below has coordinates given by , where the origin is at the center of the blades, and are in meters, and is in seconds. The blades are 7 meters long and the windmill makes one complete revolution every 28 seconds in a counterclockwise direction. The mouse starts in the 3 o'clock position and, 10.5 seconds later, loses its hold and flies off. Assume that when the mouse leaves the blade it moves along a straight line tangent to the circle on which it was previously moving. The equation of that line is y=--------+-----------x. Round to 2 decimal places if necessary.
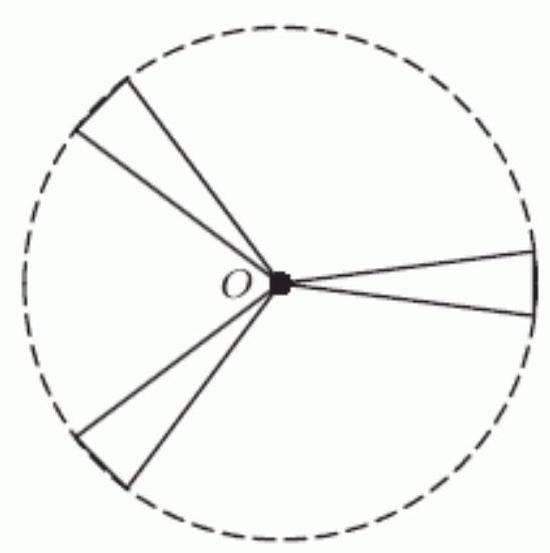


Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
28
If the circle is put into standard form
, then , and ------.
, then , and ------.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
29
If the circle is converted to the parametric equations , then h=------------,k=----------,and r=------------.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
30
The center of the circle is at .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
31
What is the radius of the circle ?

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
32
Let and parameterize a circle, with , and . What quadrant does the circle lie in?
A) The second
B) The third
C) The fourth
D) The first
A) The second
B) The third
C) The fourth
D) The first

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
33
What is the radius of the circle parameterized by ?

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
34
What is the direction of the circle parameterized by ?
A) counterclockwise
B) clockwise
A) counterclockwise
B) clockwise

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
35
The center of the circle parameterized by is at (----------,---------).

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
36
Which of the following sets of equations parameterize the circle ? Mark all that apply.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
37
Parameterize the circle of diameter 4 centered at traversed counterclockwise starting at .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
38
A bug starts at the point and moves at 5 units\second along the -axis to the point . Then, the ant moves clockwise along a circle of radius 1 centered at to the point at a speed of 4 units\second. Express the bug's coordinates as a function of time, , in seconds.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
39
Identify the center and radius of

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
40
is a circle of radius 4 centered at

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
41
is a circle of radius 3 centered at .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
42
What curve is parameterized by the functions and ? Give an implicit or explicit equation for the curve.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
43
Is the function implicit or explicit?

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
44
Is the function implicit or explicit?

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
45
Select the type of curve formed by the parametric equations and .
A) Circle
B) Parabola
C) Elipse
D) Line
A) Circle
B) Parabola
C) Elipse
D) Line

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
46
Select the type of curve formed by the parametric equations and .
A) Circle
B) Parabola
C) Elipse
D) Line
A) Circle
B) Parabola
C) Elipse
D) Line

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
47
Select the type of curve formed by the parametric equations and .
A) Circle
B) Parabola
C) Elipse
D) Hyperbola
A) Circle
B) Parabola
C) Elipse
D) Hyperbola

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
48
Select the type of curve formed by the parametric equations and .
A) Circle
B) Parabola
C) Elipse
D) Hyperbola
A) Circle
B) Parabola
C) Elipse
D) Hyperbola

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
49
If the ellipse is written in standard form , then h=-----------,k=----------,a=-----------,and b=---------.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
50
Are the parametric equations for the quarter of an ellipse centered at , starting at and ending at , given by ?

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
51
Find the upper intersection point of the ellipse and the line -2 . Round the -coordinate to 2 decimal points.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
52
Which of the following is the implicit equation for the ellipse graphed below?
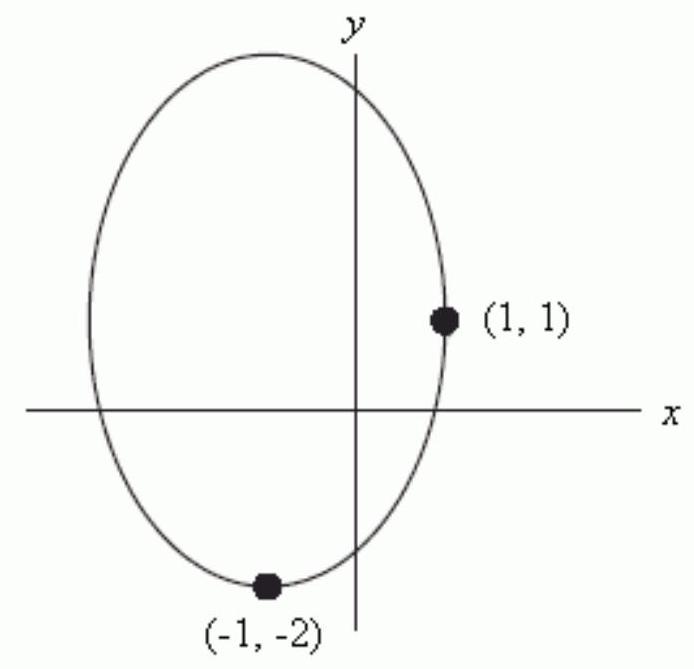
A)
B)
C)
D)

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
53
Does , parameterize the ellipse graphed below, traversed in the clockwise direction and starting at the point ?
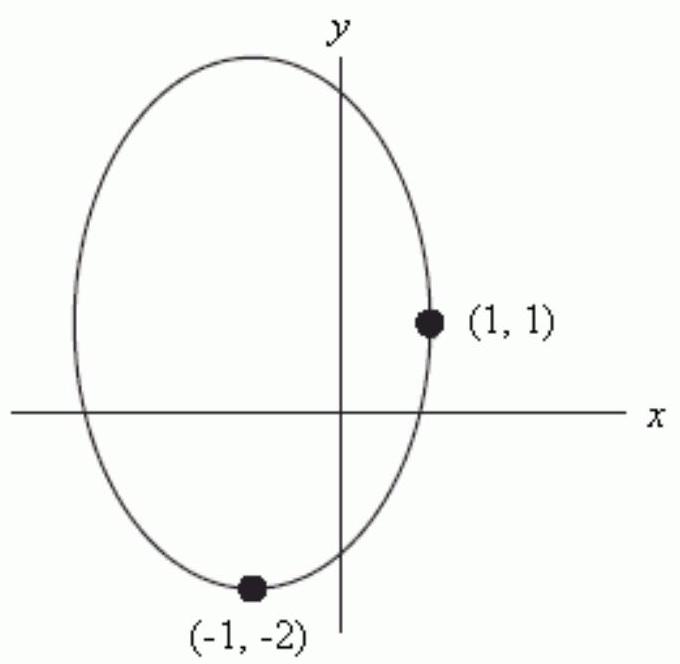


Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
54
In the ellipse given by the equations , the -values range from a minimum of ----------- to a maximum of ----------- about the midline x=----------.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
55
The ellipse given by the equations , has a height of ---------- units and a width of ---------- units.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
56
The ellipse given by the equations , has a minor axis of length ------------- units.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
57
In the ellipse given by the equation , the -values range from a minimum of --------- to a maximum of ------------about the midline x=------------.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
58
The ellipse given by the equation has a height of ---------- units and a width of ---------- units.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
59
The ellipse given by the equation has a minor axis of length -----------.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
60
Find the center of the ellipse and the lengths of the major and minor axes:

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
61
Find a parameterization of the curve so that the curve is traversed in a counter-clockwise direction starting at .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
62
Let an ellipse be parameterized by the equations
a) What is the center?
b) What is the length of the major axis?
c) What is the length of the minor axis?
d) Find an implicit equation of the curve.
a) What is the center?
b) What is the length of the major axis?
c) What is the length of the minor axis?
d) Find an implicit equation of the curve.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
63
Let an ellipse be parameterized by the equations
a) What is the center?
b) What is the length of the major axis?
c) What is the length of the minor axis?
d) Find an implicit equation of the curve.
a) What is the center?
b) What is the length of the major axis?
c) What is the length of the minor axis?
d) Find an implicit equation of the curve.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
64
Write the ellipse in the form .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
65
The polar equation is an ellipse. What is the center of this ellipse?

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
66
Parameterize the ellipse so that the parameterization starts at the point and travels clockwise.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
67
Find the equation of the ellipse centered at with horizontal axis of length 8 and vertical axis of length 12 .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
68
Parameterize the ellipse centered at the point with horizontal axis of length 4 and vertical axis of length 10 .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
69
Select the equations that describe the graph
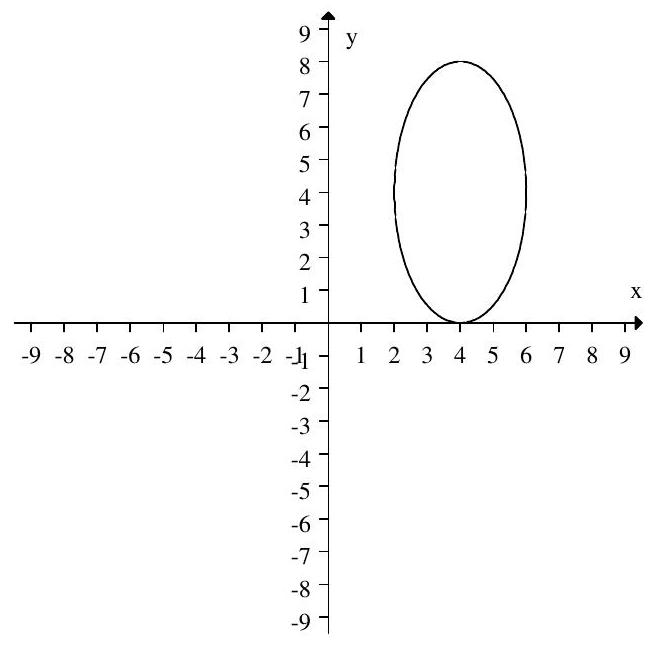
A) and
B) and
C) and
D) and

A) and
B) and
C) and
D) and

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
70
If the equation is written in standard form or , then h =-----------,k=----------,a=---------,and b =--------------.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
71
What is the center of the hyperbola ?

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
72
Does the hyperbola open left-right or up-down?

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
73
Is a vertex of the hyperbola shown below?
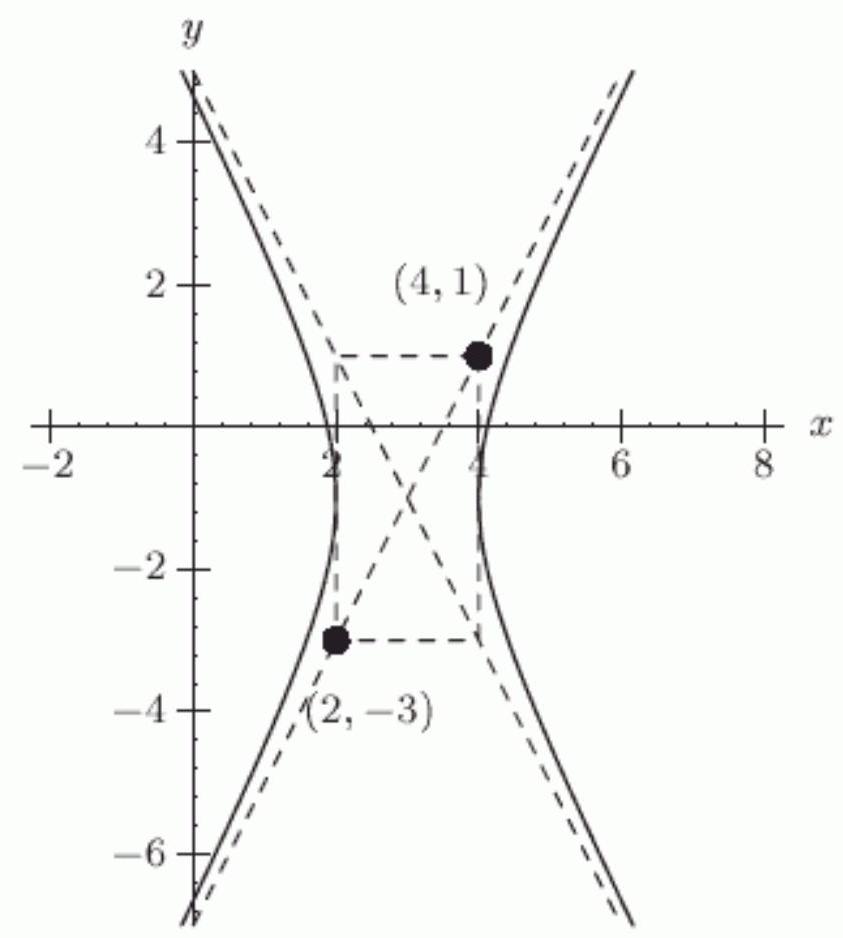


Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
74
Is an asymptote of the hyperbola shown below?
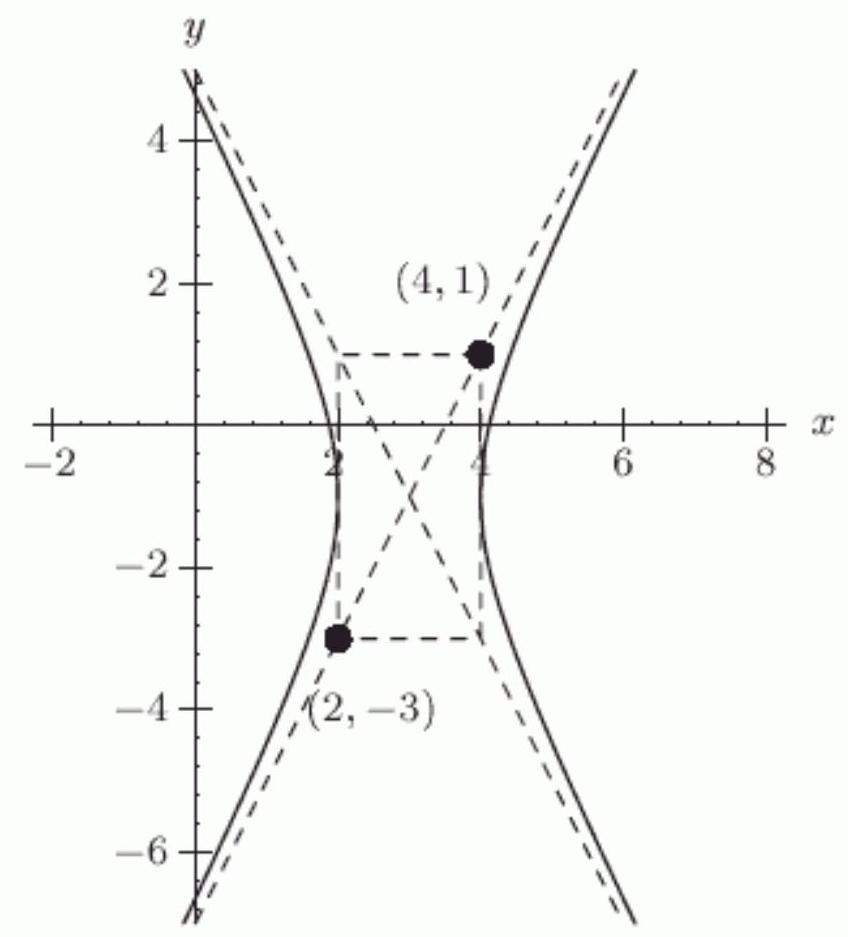


Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
75
In the hyperbola given by the equations , the left vertex is at (-----------,--------------).

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
76
In the hyperbola given by the equations , the asymptote that slopes upward has equation y=-------------x+----------. Round both answers to 2 decimal places.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
77
In the hyperbola given by the equation , the left vertex is at (-----------,-------------)

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
78
In the hyperbola given by the equation , the asymptote that slopes upward has equation . Round both answers to 2 decimal places.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
79
Parameterize the hyperbola .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
80
Parameterize the hyperbola

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck


