Deck 10: Inverse, Exponential, and Logarithmic Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/292
Play
Full screen (f)
Deck 10: Inverse, Exponential, and Logarithmic Functions
1
Determine whether or not the function is one-to-one.
-
-
True
2
Determine whether or not the function is one-to-one.
-
-
False
3
Determine whether or not the function is one-to-one.
-
-
False
4
Determine whether or not the function is one-to-one.
-This chart shows the number of hits for five Little League baseball teams.
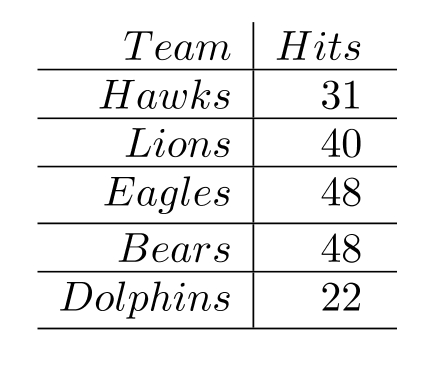
-This chart shows the number of hits for five Little League baseball teams.


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
5
Determine whether or not the function is one-to-one.
-This chart shows the number of living relatives in five families.

-This chart shows the number of living relatives in five families.


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
6
Determine whether or not the function is one-to-one.
-The function that pairs the temperature in degrees Fahrenheit of a cup of coffee with its temperature in degrees Celsius.
-The function that pairs the temperature in degrees Fahrenheit of a cup of coffee with its temperature in degrees Celsius.

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
7
Determine whether or not the function is one-to-one.
-The function that pairs the radius of a spherical bowling ball with its volume.
-The function that pairs the radius of a spherical bowling ball with its volume.

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
8
Determine whether or not the function is one-to-one.
-
-

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
9
Determine whether or not the function is one-to-one.
-
-

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
10
Determine whether or not the function is one-to-one.
-
-

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
11
Determine whether or not the function is one-to-one.
-
-

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
12
Determine whether or not the function is one-to-one.
-
-

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
13
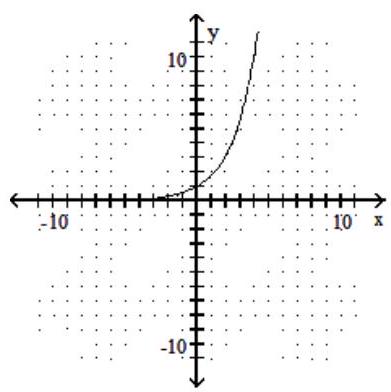
Determine whether or not the function is one-to-one.
-
-


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
14
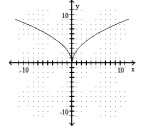
Determine whether or not the function is one-to-one.
-
-


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
15
If the following defines a one-to-one function, find its inverse. If not, write "Not one-to-one."
-
A)
B)
C)
D) Not one-to-one
-
A)
B)
C)
D) Not one-to-one

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
16
If the following defines a one-to-one function, find its inverse. If not, write "Not one-to-one."
-
A)
B)
C) Not one-to-one
D)
-
A)
B)
C) Not one-to-one
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
17
If the following defines a one-to-one function, find its inverse. If not, write "Not one-to-one."
-
A)
B)
C) Not one-to-one
D)
-
A)
B)
C) Not one-to-one
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
18
If the following defines a one-to-one function, find its inverse. If not, write "Not one-to-one."
-
A)
B)
C) Not one-to-one
D)
-
A)
B)
C) Not one-to-one
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
19
If the following defines a one-to-one function, find its inverse. If not, write "Not one-to-one."
-
A) Not one-to-one
B)
C)
D)
-
A) Not one-to-one
B)
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
20
If the following defines a one-to-one function, find its inverse. If not, write "Not one-to-one."
-
A) Not one-to-one
B)
C)
D)
-
A) Not one-to-one
B)
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
21
If the following defines a one-to-one function, find its inverse. If not, write "Not one-to-one."
-
A)
B)
C) Not one-to-one
D)
-
A)
B)
C) Not one-to-one
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
22
If the following defines a one-to-one function, find its inverse. If not, write "Not one-to-one."
-
A)
B) Not one-to-one
C)
D)
-
A)
B) Not one-to-one
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
23
If the following defines a one-to-one function, find its inverse. If not, write "Not one-to-one."
-
A)
B) Not one-to-one
C)
D)
-
A)
B) Not one-to-one
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
24
If the following defines a one-to-one function, find its inverse. If not, write "Not one-to-one."
-
A)
B)
C) Not one-to-one
D)
-
A)
B)
C) Not one-to-one
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
25
Find the indicated value.
-Let
A) 27
B) 81
C) 243
D) 12
-Let
A) 27
B) 81
C) 243
D) 12

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
26
Find the indicated value.
-Let
A) -8
B)
C)
D)
-Let
A) -8
B)
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
27
Find the indicated value.
-Let
A)
B)
C) 2
D) 3
-Let
A)
B)
C) 2
D) 3

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
28
Find the indicated value.
-Let
A) -2
B) -4
C) 4
D)
-Let
A) -2
B) -4
C) 4
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
29
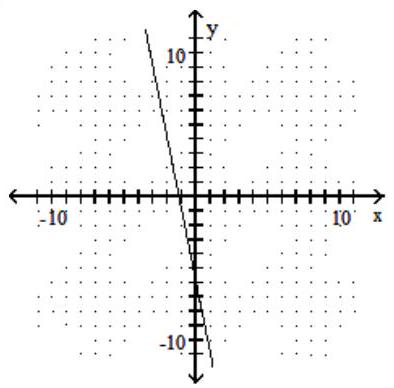
Use the horizontal line test to determine if the function is one-to-one.
-
-


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
30
Use the horizontal line test to determine if the function is one-to-one.
-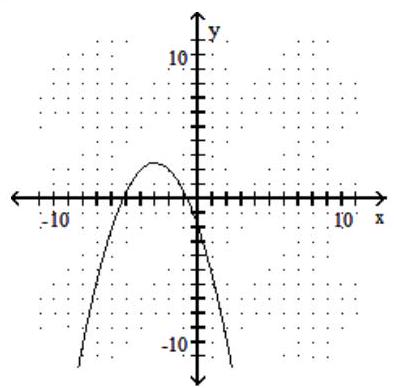
-


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
31
Use the horizontal line test to determine if the function is one-to-one.
-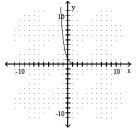
-


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
32
Use the horizontal line test to determine if the function is one-to-one.
-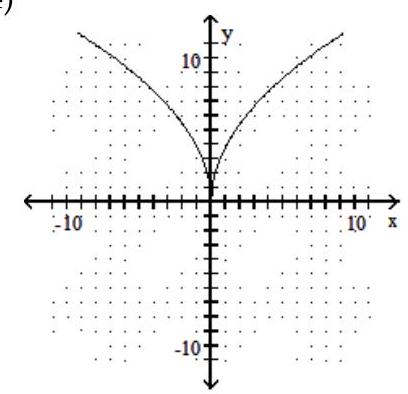
-


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
33
Use the horizontal line test to determine if the function is one-to-one.
-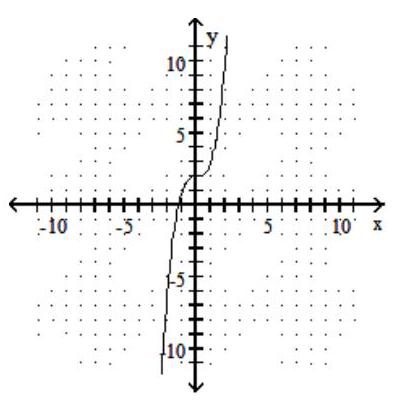
-


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
34
Graph the given function as a solid line (or curve) and its inverse as a dashed line (or curve) on the same set of axes.
-
A)
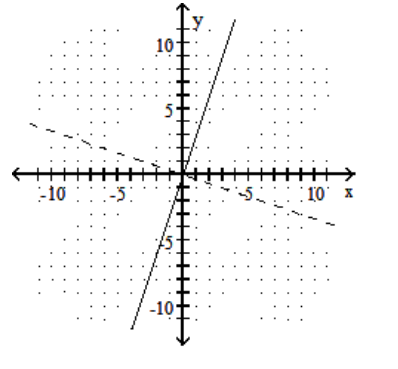
B)
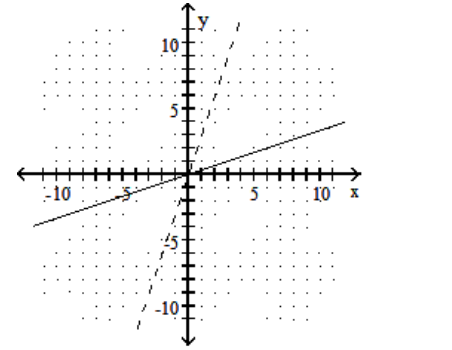
C)
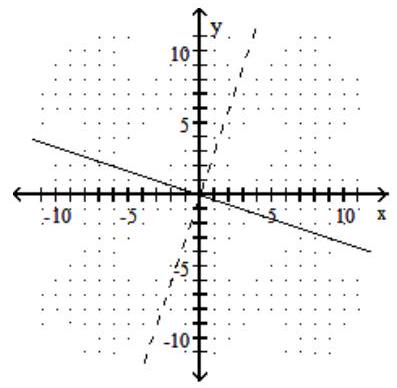
D)
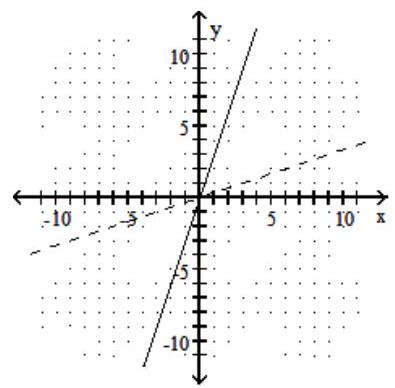
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
35
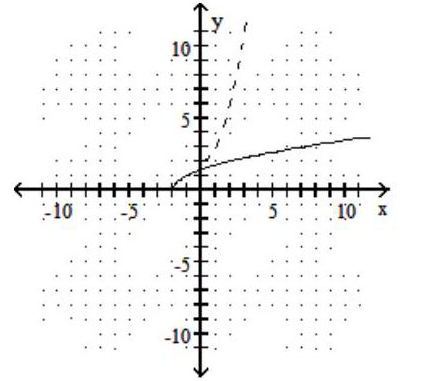
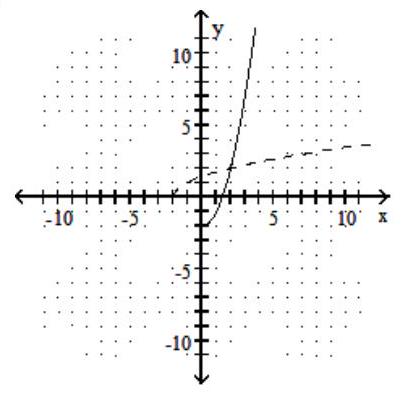
Graph the given function as a solid line (or curve) and its inverse as a dashed line (or curve) on the same set of axes.
-
A)
B)
C)
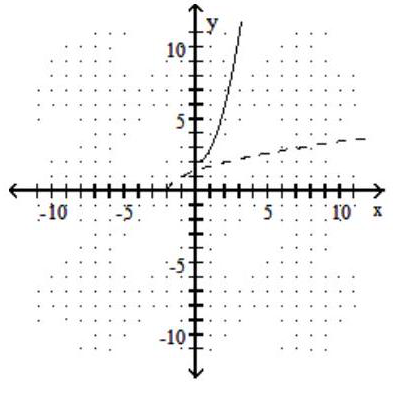
D)
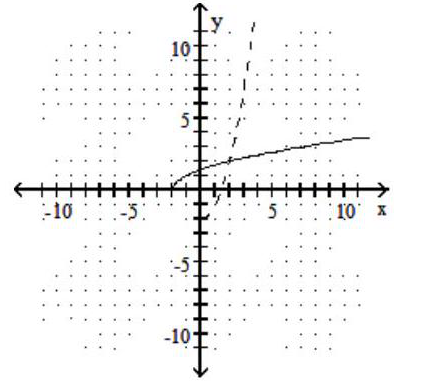
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
36
Graph the given function as a solid line (or curve) and its inverse as a dashed line (or curve) on the same set of axes.
-
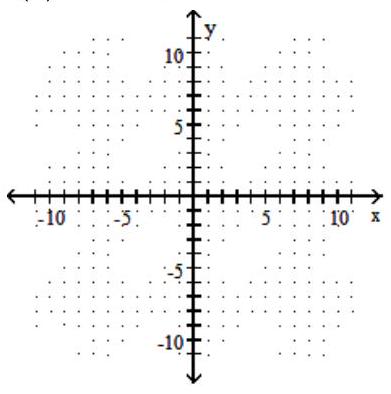
A)
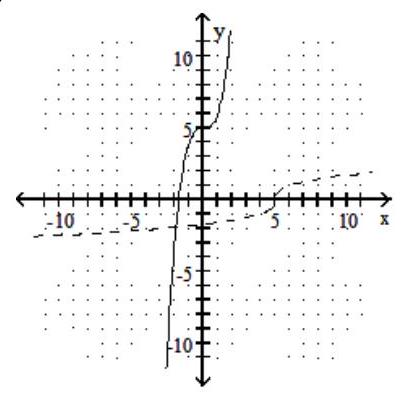
B)
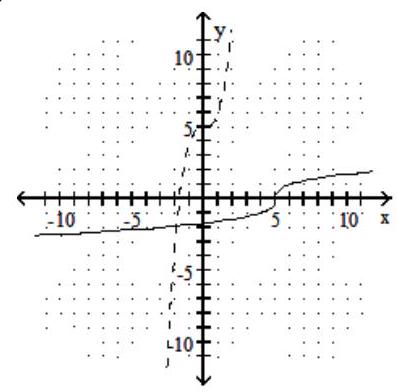
C)
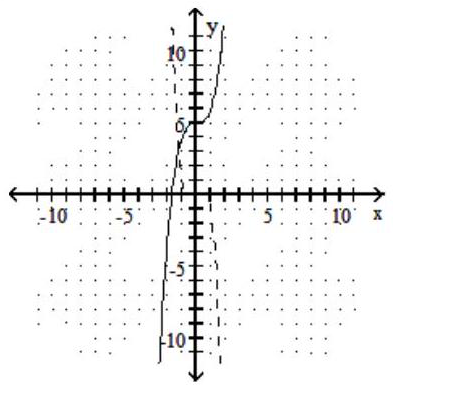
D)
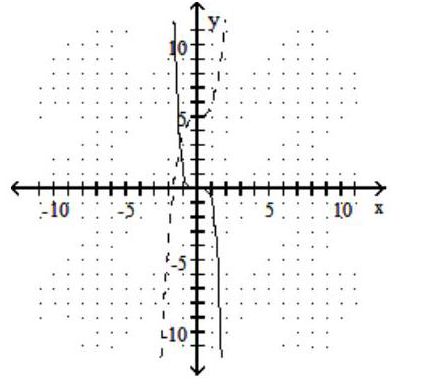
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
37
Graph the given function as a solid line (or curve) and its inverse as a dashed line (or curve) on the same set of axes.
-
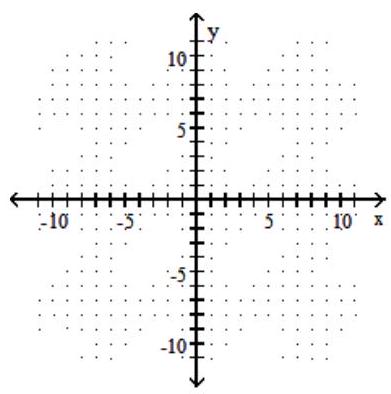
A)
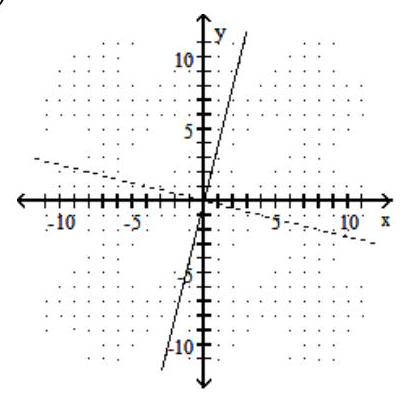
B)
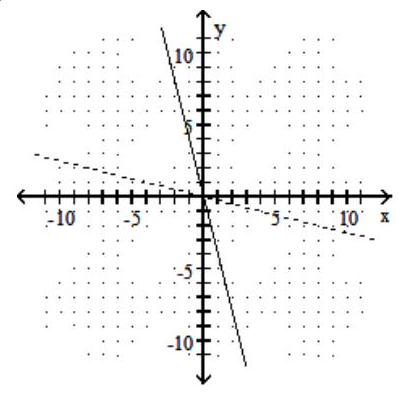 C)
C)
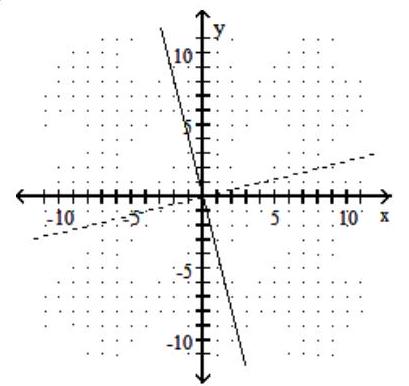 D)
D)
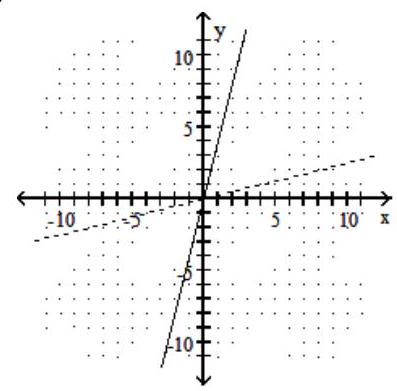
-

A)

B)
 C)
C) D)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
38
Graph the given function as a solid line (or curve) and its inverse as a dashed line (or curve) on the same set of axes.
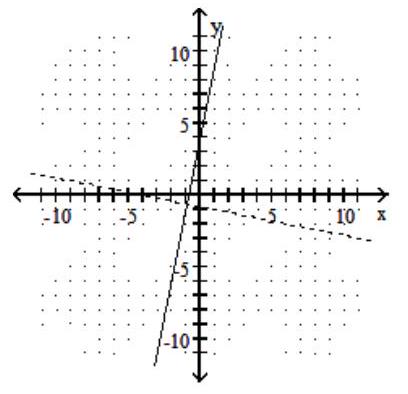
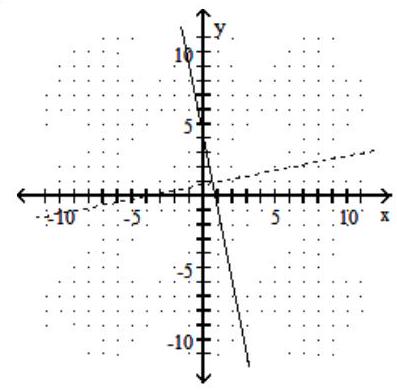
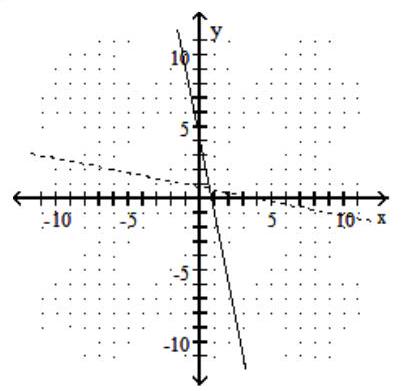
-
A)
B)
C)
D)
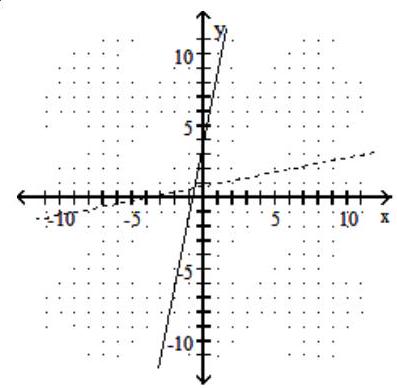
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
39
Graph the given function as a solid line (or curve) and its inverse as a dashed line (or curve) on the same set of axes.
-
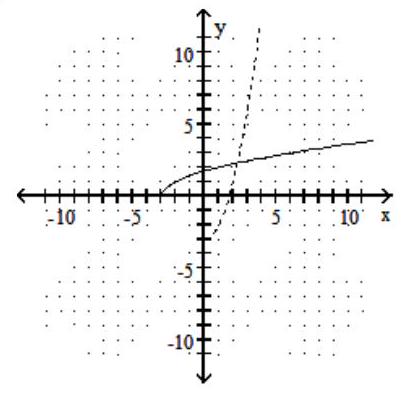
A)
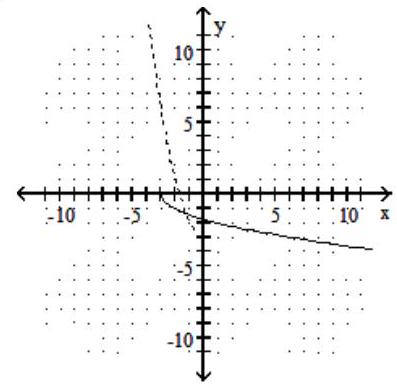
B)
C)
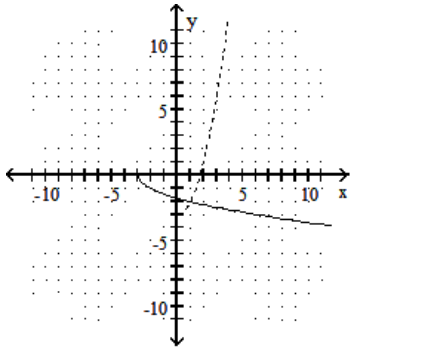
D)
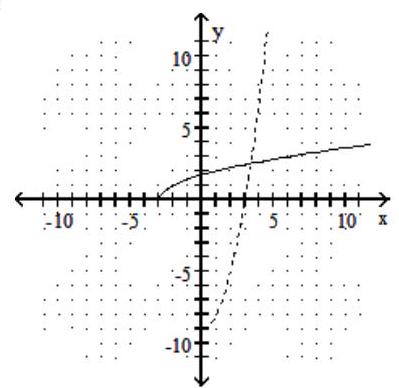
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
40
Graph the function.
-
A)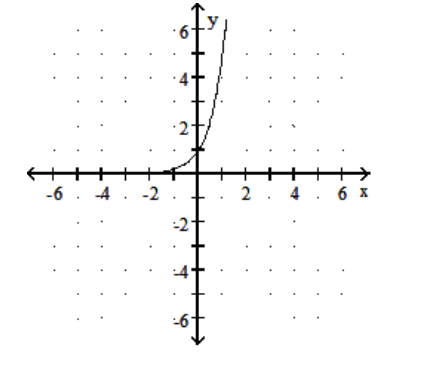
B)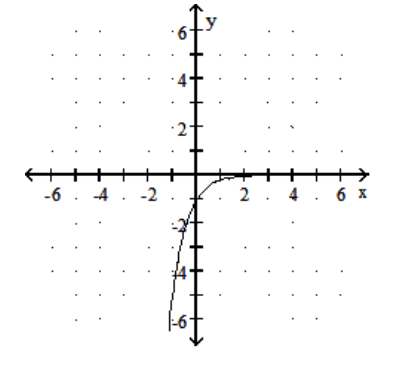
C)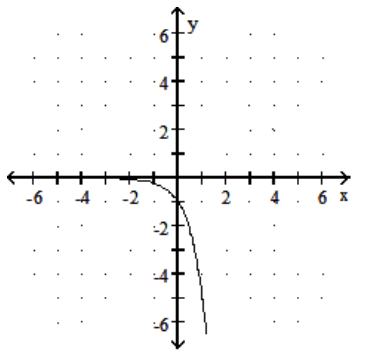
D)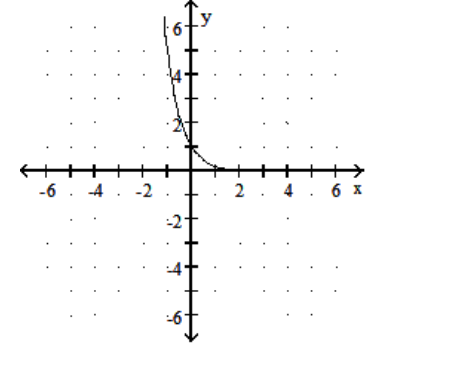
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
41
Graph the function.
-
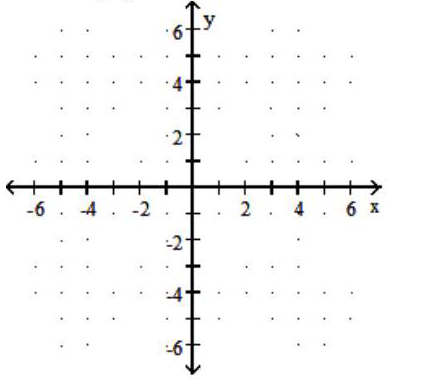
A)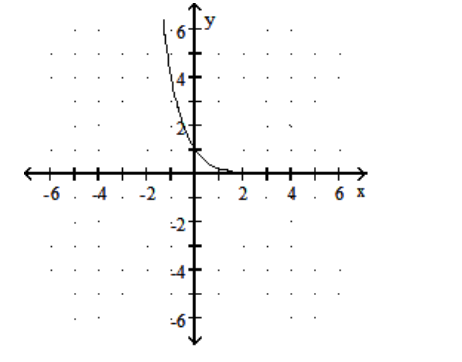
B)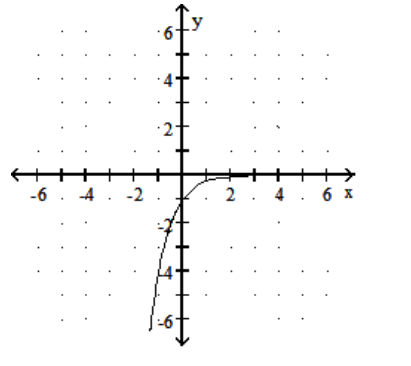
C)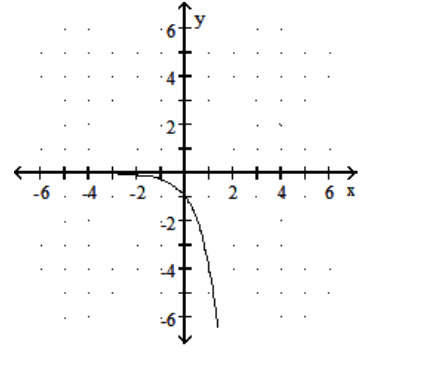
D)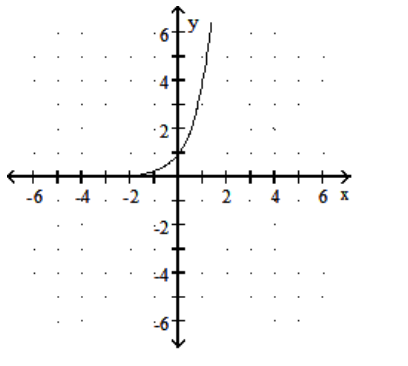
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
42
Graph the function.
-
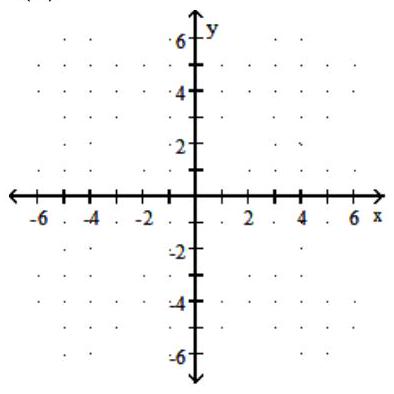
A)
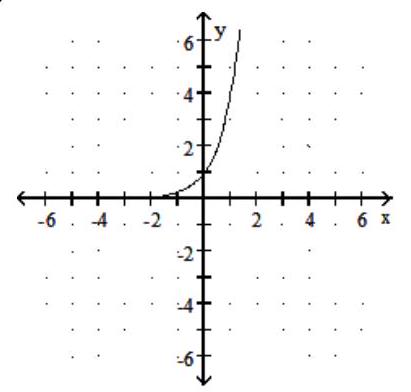
B)
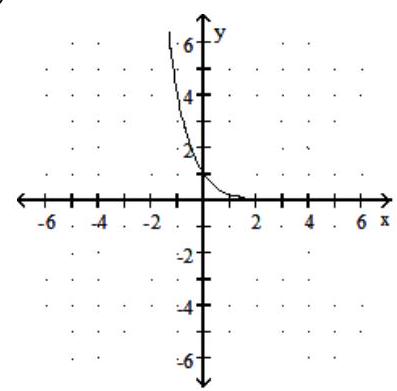
C)
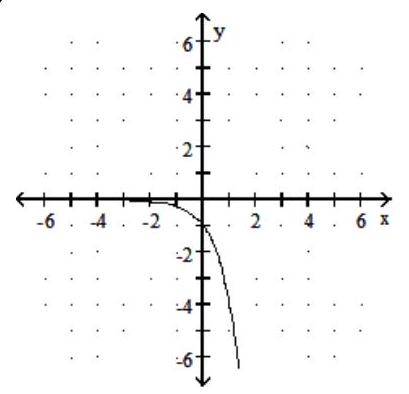
D)
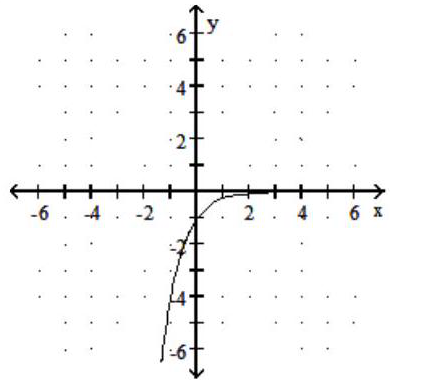
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
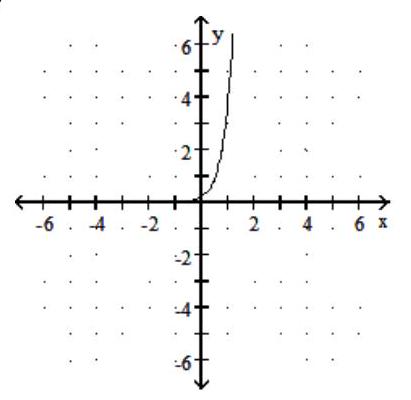
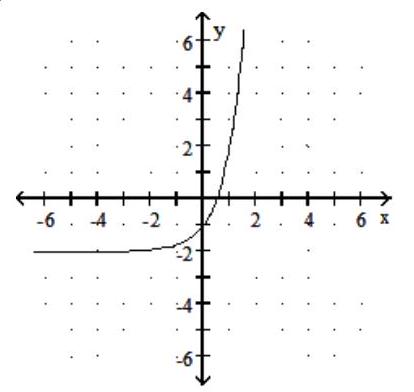
43
Graph the function.
-
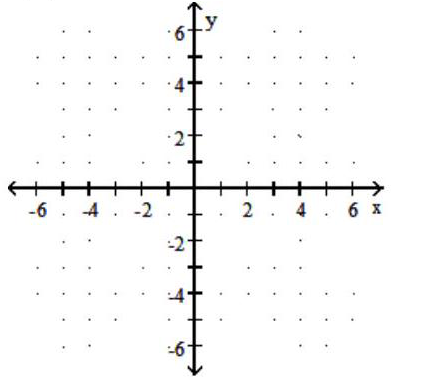
A)
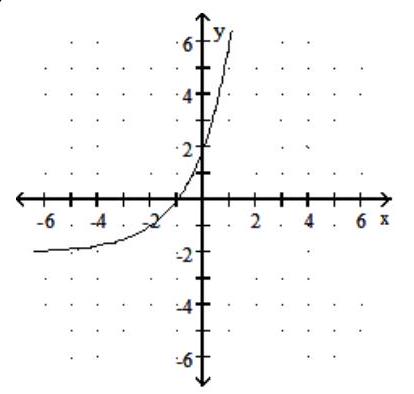
B)
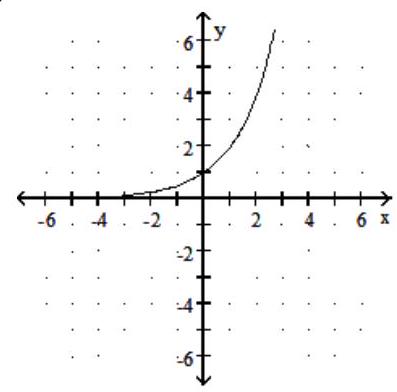
C)
D)
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
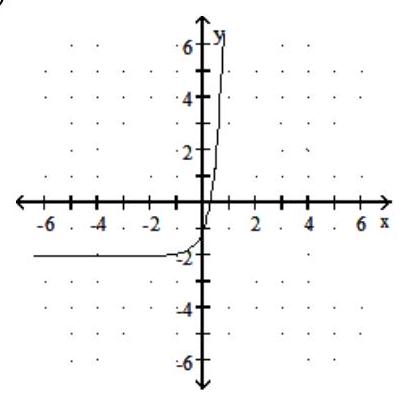
44
Graph the function.
-
A)
B)
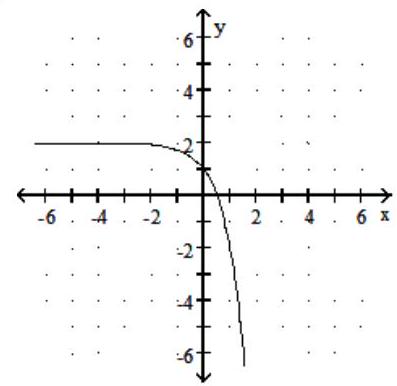
C)
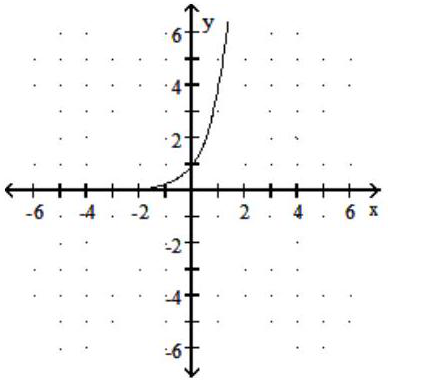
D)
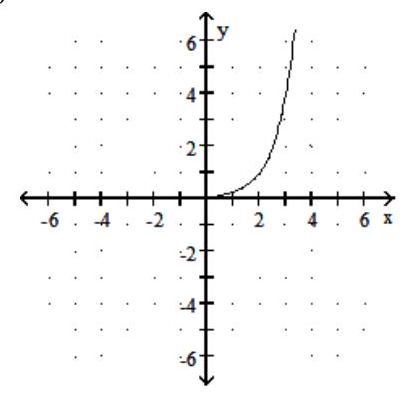
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the equation.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the equation.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
47
Solve the equation.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
48
Solve the equation.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the equation.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the equation.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the equation.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
52
Solve the equation.
-
A)
B) \{3\}
C)
D)
-
A)
B) \{3\}
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
53
Solve the equation.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
54
Using the exponential key of a calculator to find an approximation to the nearest thousandth.
-
A)
B) 509.316
C) 289
D) 37.4
-
A)
B) 509.316
C) 289
D) 37.4

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
55
Using the exponential key of a calculator to find an approximation to the nearest thousandth.
-
A) 192.533
B) 0.033
C) 1.49
D) 1.6
-
A) 192.533
B) 0.033
C) 1.49
D) 1.6

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
56
Using the exponential key of a calculator to find an approximation to the nearest thousandth.
-2.5973 .8
A) 9.869
B) 32.04
C) 6.744
D) 37.583
-2.5973 .8
A) 9.869
B) 32.04
C) 6.744
D) 37.583

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
57
Using the exponential key of a calculator to find an approximation to the nearest thousandth.
-
A) -30.824
B) 0.152
C) 0.028
D) 0.102
-
A) -30.824
B) 0.152
C) 0.028
D) 0.102

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
58
An accountant tabulated a firm's profits for four recent years in the following table:
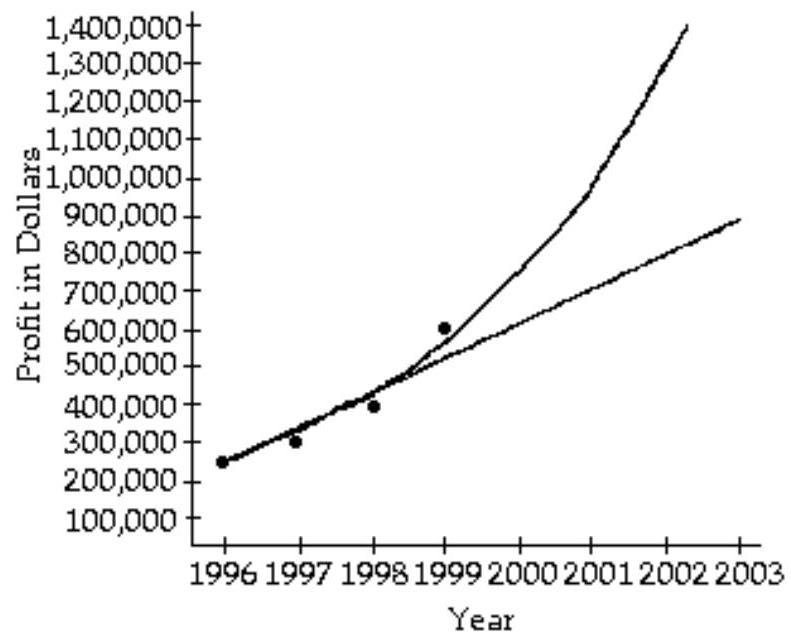
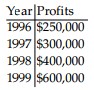 The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimate future profits. Use the linear graph to estimate the profits in the year 2001.
The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimate future profits. Use the linear graph to estimate the profits in the year 2001.
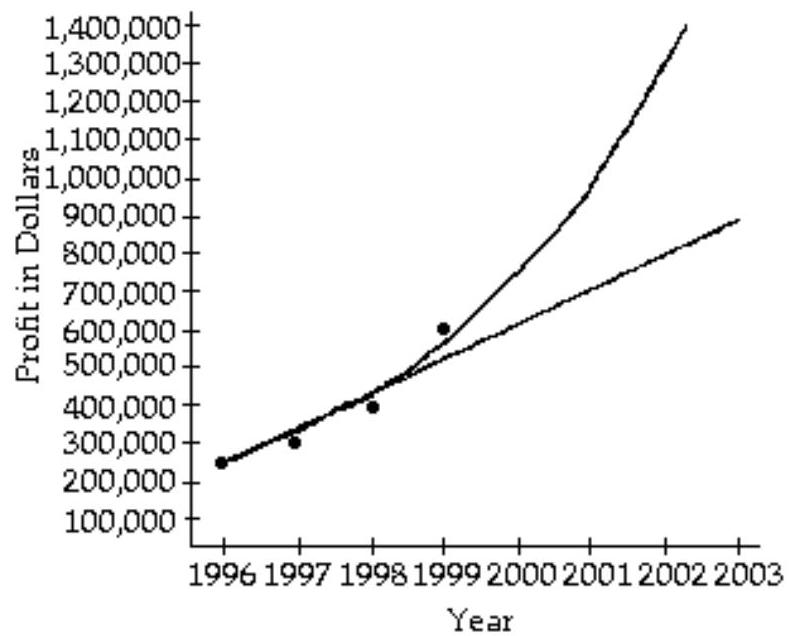
A) About
B) About
C) About
D) About
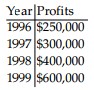 The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimate future profits. Use the linear graph to estimate the profits in the year 2001.
The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimate future profits. Use the linear graph to estimate the profits in the year 2001.
A) About
B) About
C) About
D) About

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
59
An accountant tabulated a firm's profits for four recent years in the following table:
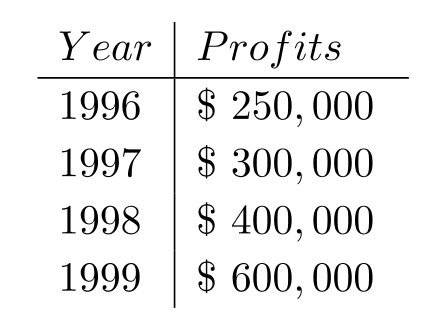
The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimate future profits. Use the exponential graph to estimate the profits in the year 2002.
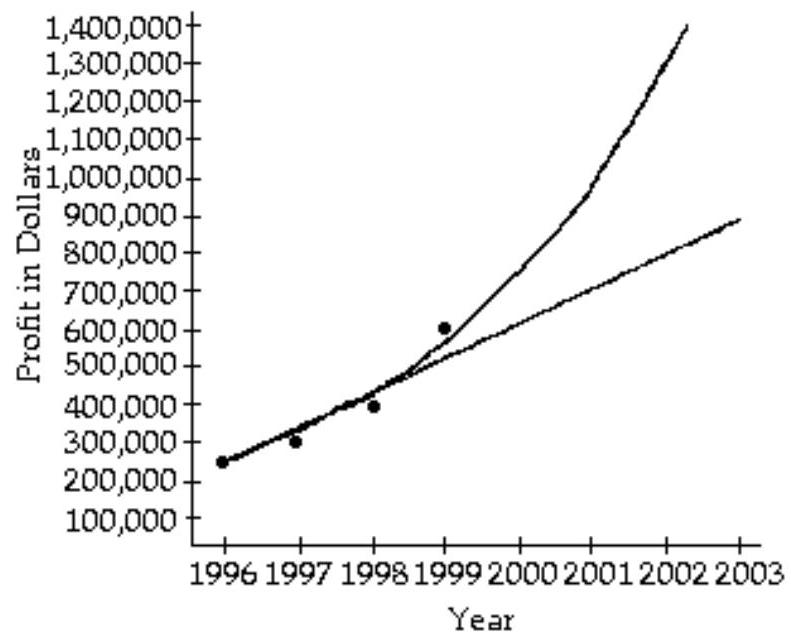
A) About
B) About
C) About \$1,300,000
D) About
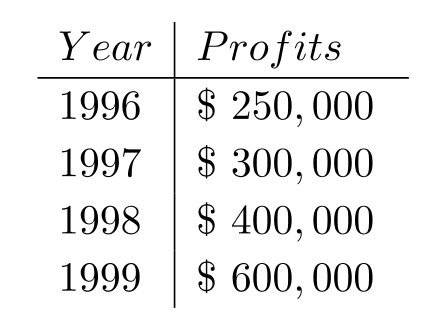
The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimate future profits. Use the exponential graph to estimate the profits in the year 2002.

A) About
B) About
C) About \$1,300,000
D) About

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
60
An accountant tabulated a firm's profits for four recent years in the following table:
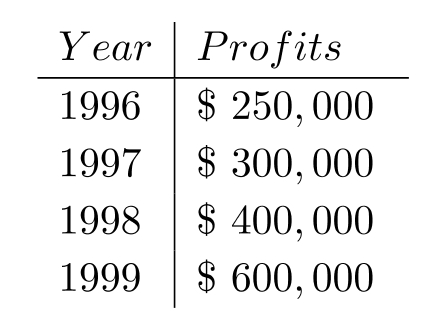
The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimate future profits. Use the linear graph to estimate the profits in the year 2002.
A) About
B) About
C) About \$1,000,000
D) About
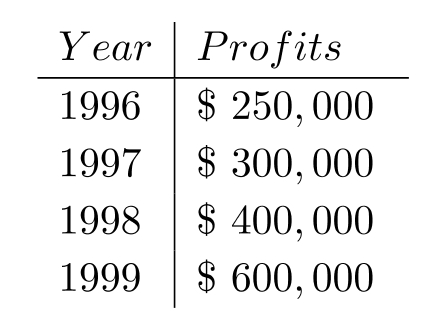
The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimate future profits. Use the linear graph to estimate the profits in the year 2002.

A) About
B) About
C) About \$1,000,000
D) About

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
61
An accountant tabulated a firm's profits for four recent years in the following table:
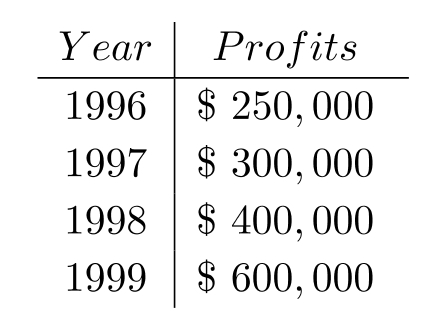
The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimate future profits. Use the exponential graph to estimate the profits in the year 2001.
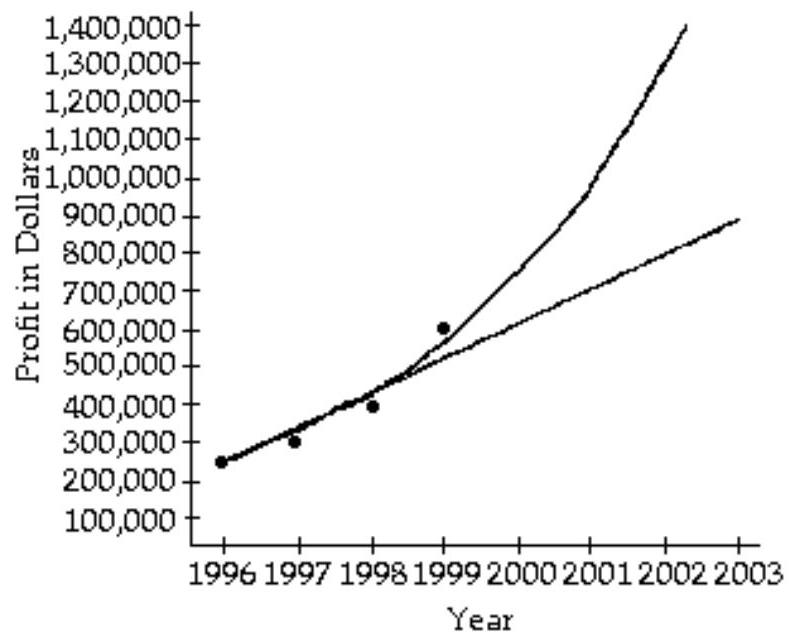
A) About \$1,000,000
B) About
C) About \$1,300,000
D) About
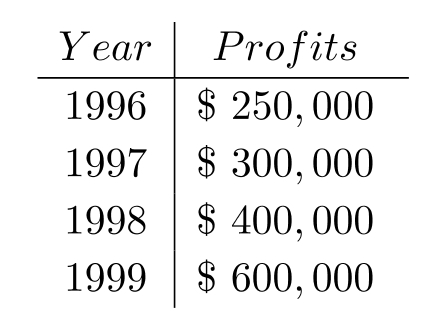
The accountant then fit both a linear graph and an exponential curve (seen below) to the data, in order to estimate future profits. Use the exponential graph to estimate the profits in the year 2001.

A) About \$1,000,000
B) About
C) About \$1,300,000
D) About

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
62
A computer is purchased for . Its value each year is about of the value the preceding year. Its value, in dollars, after years is given by the exponential function . Find the value of the computer after 4 years.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
63
A city is growing at the rate of annually. If there were residents in the city in 1994 , find how many (to the nearest ten-thousand) were living in that city in 2000. Use
A)
B)
C)
D) 320,000
A)
B)
C)
D) 320,000

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
64
The amount of particulate matter left in solution during a filtering process decreases by the equation , where is the number of filtering steps. Find the amounts left for and . (Round to the nearest whole number.)
A) 200,800
B) 200,6
C) 200,50
D) 400,50
A) 200,800
B) 200,6
C) 200,50
D) 400,50

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
65
The number of dislocated electric impulses per cubic inch in a transformer increases when lightning strikes by , where is the time in milliseconds of the lightning strike. Find the number of dislocated impulses at and .
A) 13,
B)
C)
D)
A) 13,
B)
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
66
The number of bacteria growing in an incubation culture increases with time according to , where is time in days. Find the number of bacteria when and .
A) 47,
B)
C)
D)
A) 47,
B)
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
67
The half-life of a certain radioactive substance is 36 years. Suppose that at time , there are of the substance. Then after years, the number of grams of the substance remaining will be . How many grams of the substance will remain after 198 years?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
68
The number of bacteria growing in an incubation culture increases with time according to , where is time in days. Find the number of bacteria when .
A) 26,800
B) 13,400
C) 40,200
D) 6700
A) 26,800
B) 13,400
C) 40,200
D) 6700

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
69
The number of bacteria growing in an incubation culture increases with time according to , where is time in days. After how many days will the number of bacteria in the culture be 563,200 ?(Hint: Let .)
A) 6 days
B) 10 days
C) 1 day
D) 3 days
A) 6 days
B) 10 days
C) 1 day
D) 3 days

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
70
Why can't we call an exponential function?

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
71
Why can't have an -intercept?

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
72
What are the domain and range for the equation ?
A) Domain: ; range:
B) Domain: ; range:
C) Domain: ; range:
D) ; range:
A) Domain: ; range:
B) Domain: ; range:
C) Domain: ; range:
D) ; range:

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
73
With the exponential function , why must ?

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
74
The table below gives the actual values of the population of a small island in the Pacific Ocean. The population is modeled by the equation , where represents the population of the island in 1990.
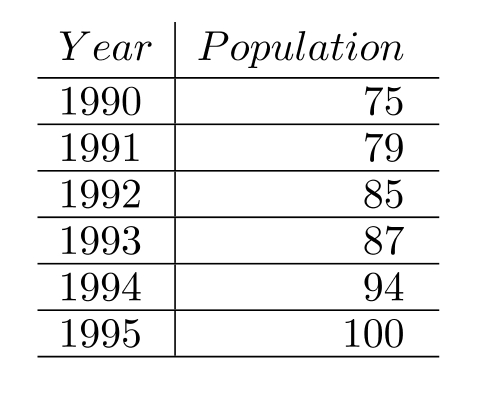
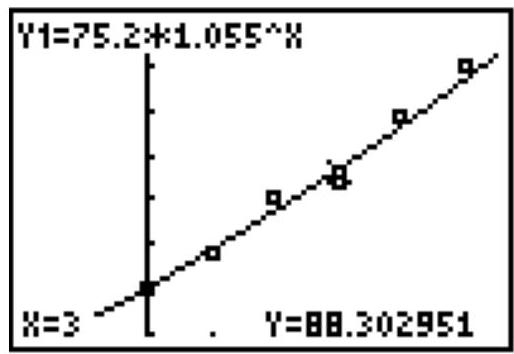
For the point displayed in the calculator screen above, how does the model compare to the actual?
A) The display indicates that for the year 1993, the model gives a value of about 87 people, which is slightly less than the actual value of 88 people.
B) The display indicates that for the year 1990, the model gives a value of 75.2 people, which is slightly more than the actual value of 75 people.
C) The display indicates that for the year 1993, the model gives a value of about 88 people, which is slightly more than the actual value of 87 people.
D) The display indicates that for the year 1995 , the model gives a value of about 88 people, which is slightly more than the actual value of 87 people.


For the point displayed in the calculator screen above, how does the model compare to the actual?
A) The display indicates that for the year 1993, the model gives a value of about 87 people, which is slightly less than the actual value of 88 people.
B) The display indicates that for the year 1990, the model gives a value of 75.2 people, which is slightly more than the actual value of 75 people.
C) The display indicates that for the year 1993, the model gives a value of about 88 people, which is slightly more than the actual value of 87 people.
D) The display indicates that for the year 1995 , the model gives a value of about 88 people, which is slightly more than the actual value of 87 people.

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
75
Evaluate the logarithm.
-
A) -1
B) 0
C) 3
D) 1
-
A) -1
B) 0
C) 3
D) 1

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
76
Evaluate the logarithm.
-
A) -2
B) 5
C) 2
D) -5
-
A) -2
B) 5
C) 2
D) -5

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
77
Evaluate the logarithm.
-
A) 49
B) -49
C) -3
D) 3
-
A) 49
B) -49
C) -3
D) 3

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
78
Evaluate the logarithm.
-
A) 3
B) -100
C) -3
D) 100
-
A) 3
B) -100
C) -3
D) 100

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
79
Evaluate the logarithm.
-
A) 1
B) 2
C) -2
D) 0
-
A) 1
B) 2
C) -2
D) 0

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck
80
Evaluate the logarithm.
-
A) 2
B) -2
C) 1
D) -1
-
A) 2
B) -2
C) 1
D) -1

Unlock Deck
Unlock for access to all 292 flashcards in this deck.
Unlock Deck
k this deck


