Deck 11: Nonlinear Functions, Conic Sections, and Nonlinear Systems
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/233
Play
Full screen (f)
Deck 11: Nonlinear Functions, Conic Sections, and Nonlinear Systems
1
Graph the function.
-f(x)=|-1-x|
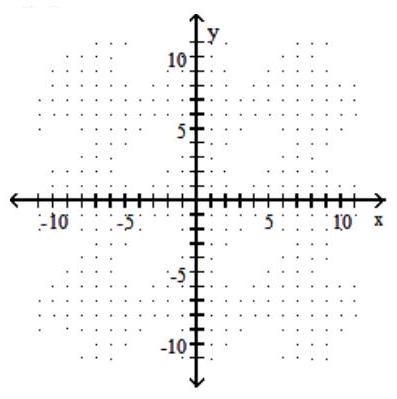
A)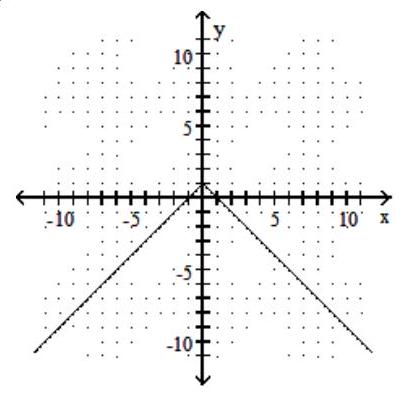
B)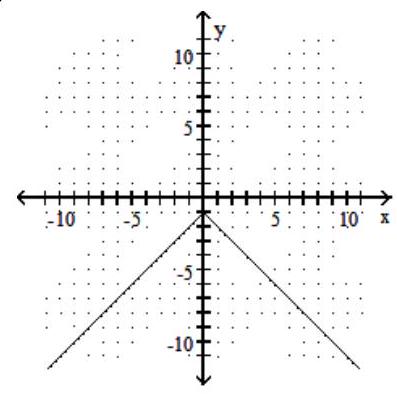
C)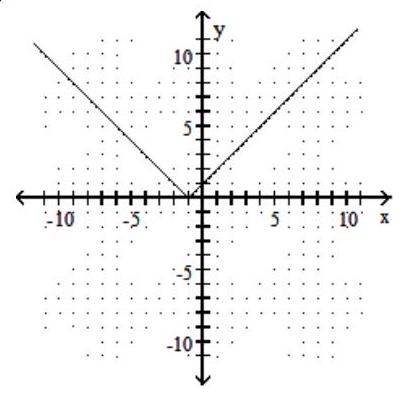
D)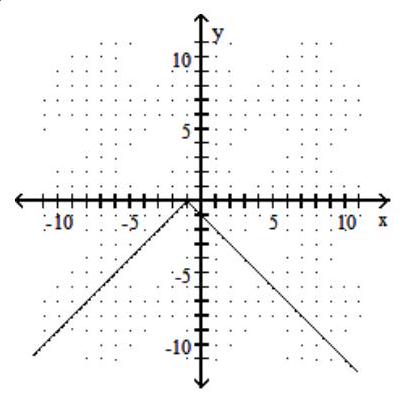
-f(x)=|-1-x|

A)

B)

C)

D)


2
Graph the function.
-f(x)=4|x|-9
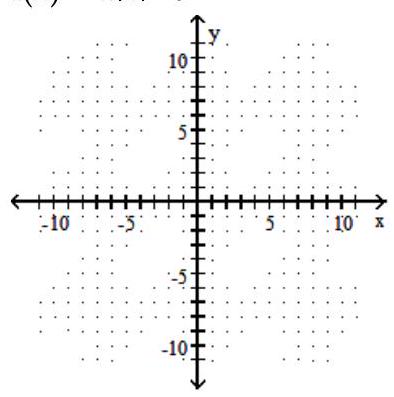
A)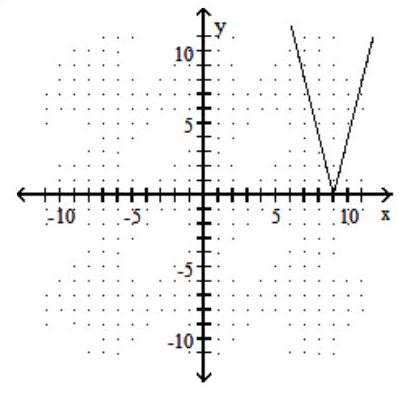
B)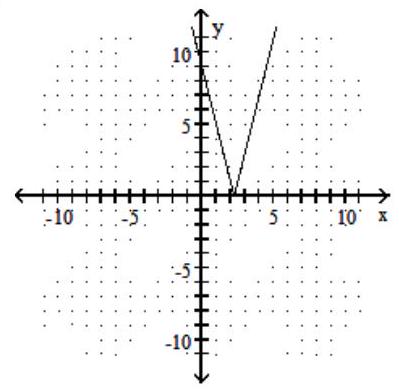
C)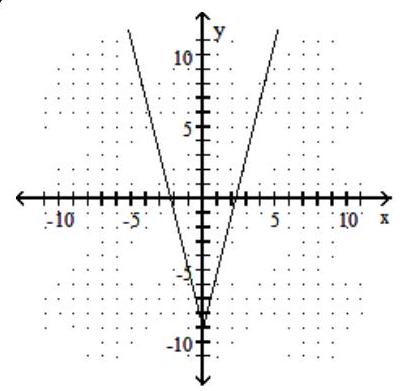
D)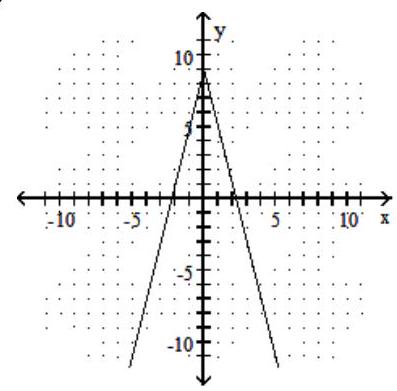
-f(x)=4|x|-9

A)

B)

C)

D)


3
Graph the function.
-f(x)=|x-8|-6
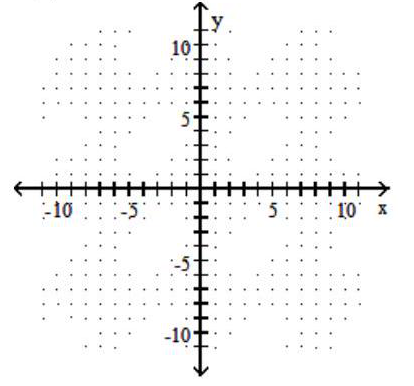
A)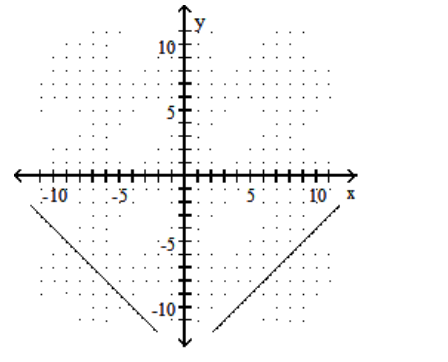
B)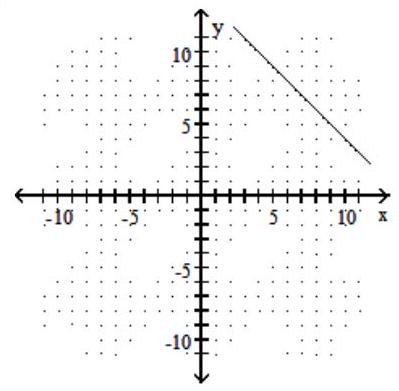
C)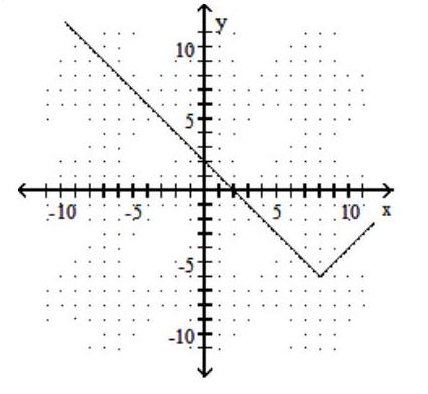
D)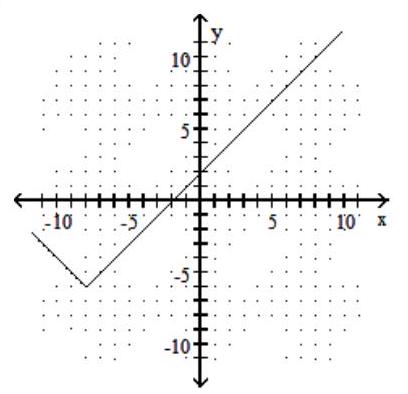
-f(x)=|x-8|-6

A)

B)

C)

D)


4
Graph the function.
-f(x)=3|x-5|-8
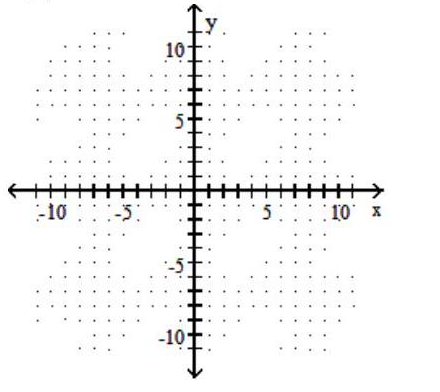
A)
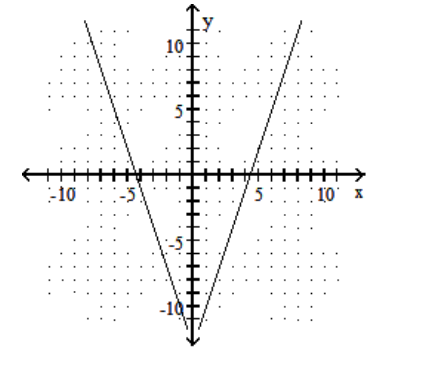
B)
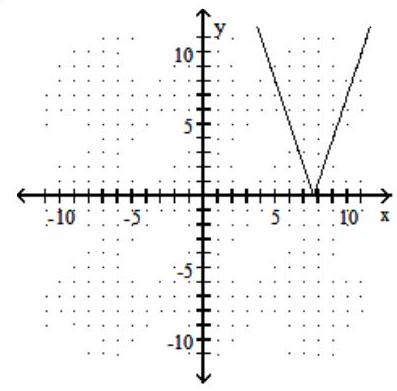
C)
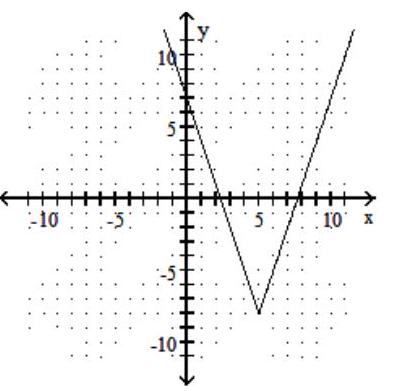
D)
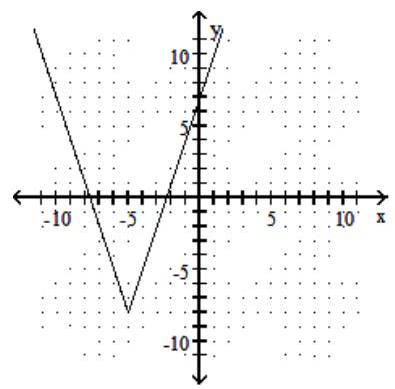
-f(x)=3|x-5|-8

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
5
Graph the rational function.
-f(x) =
A)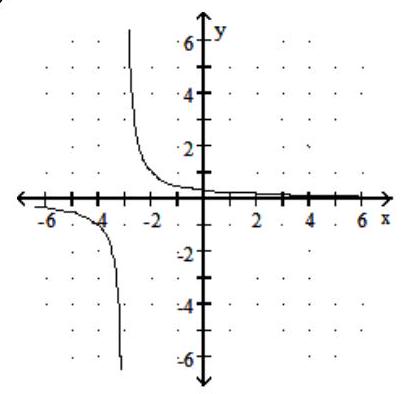
B)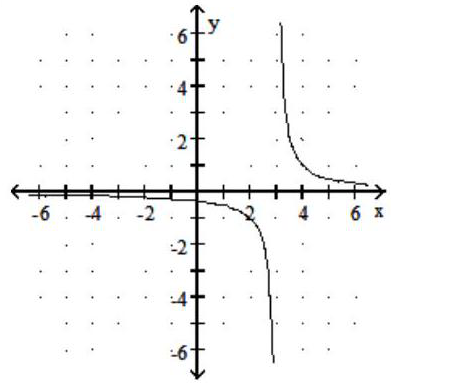
C)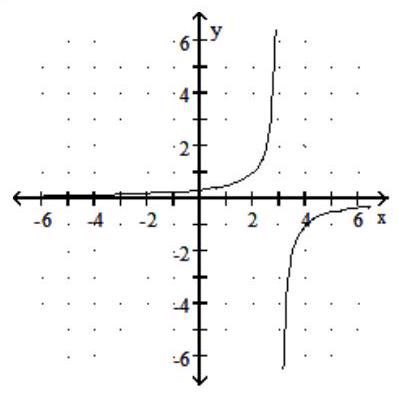
D)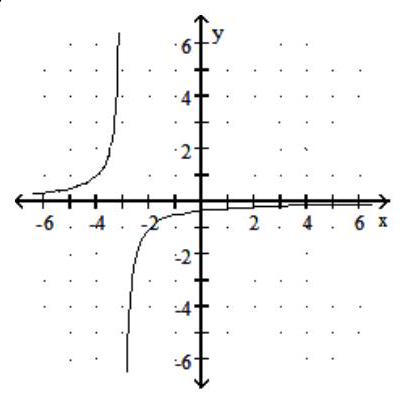
-f(x) =

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
6
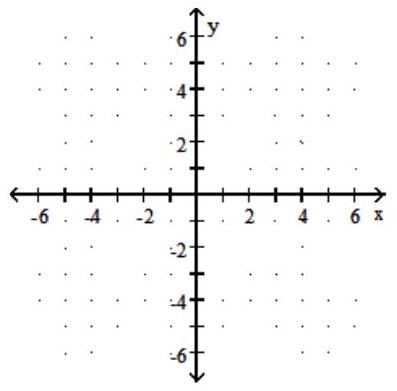
Graph the rational function.
-f(x) =
A)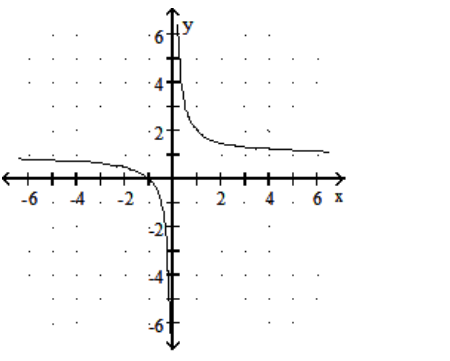
B)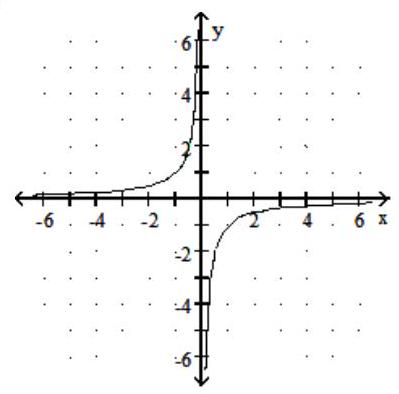
C)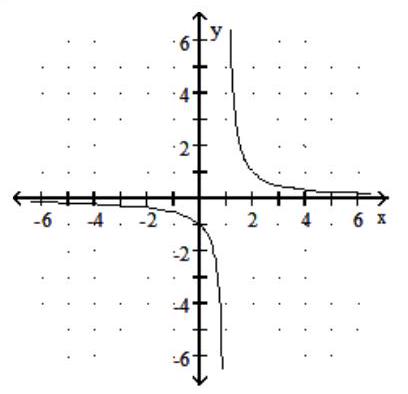
D)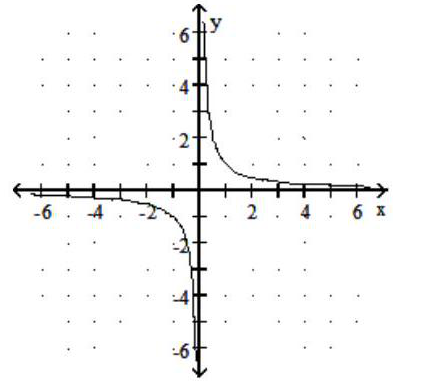
-f(x) =

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
7
Graph the rational function.
-f(x) = -
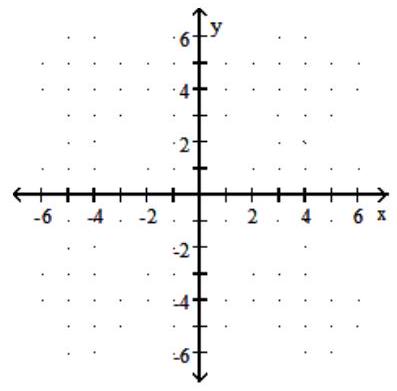
A)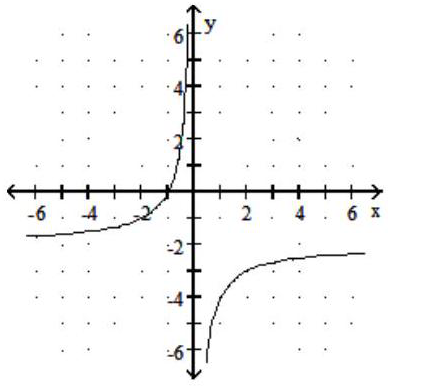
B)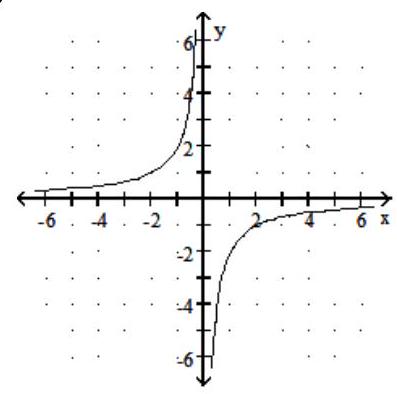
C)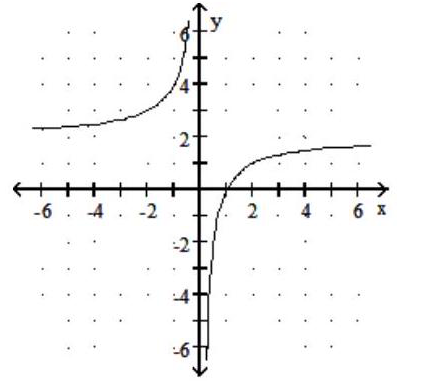
D)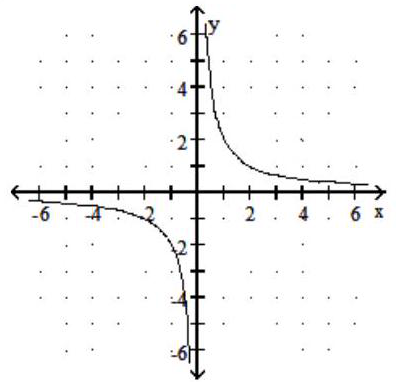
-f(x) = -

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
8
Graph the rational function.
-f(x) = -
A)
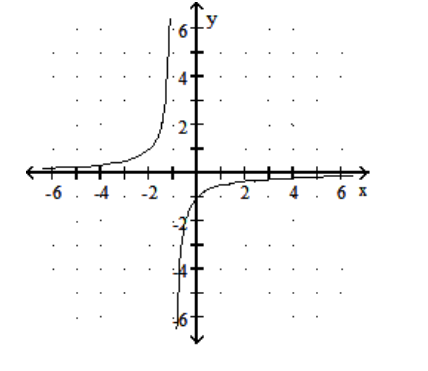
B)
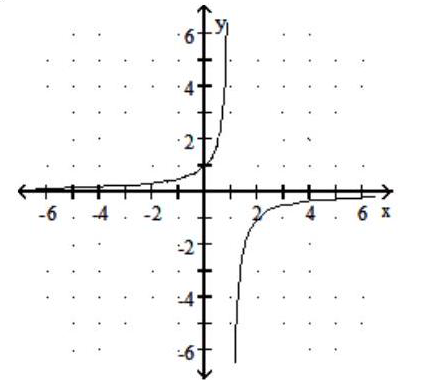
C)
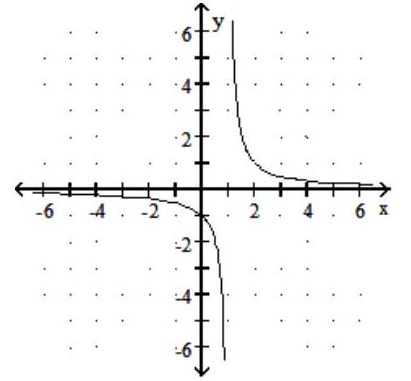
D)
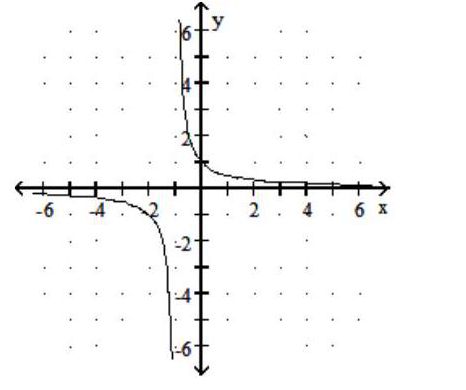
-f(x) = -

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
9
Graph the rational function.
-f(x) = + 3
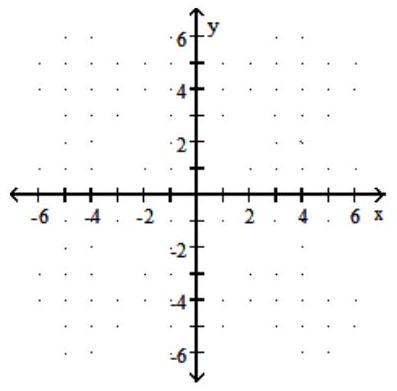
A)
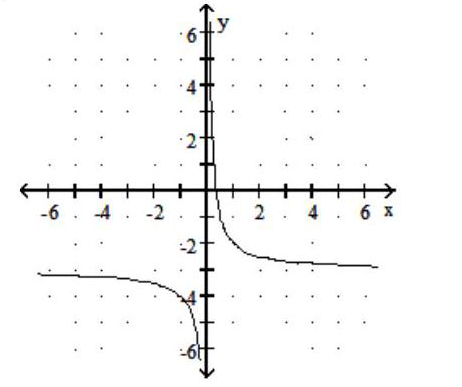
B)
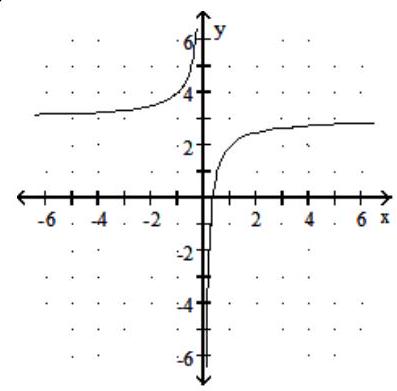
C)
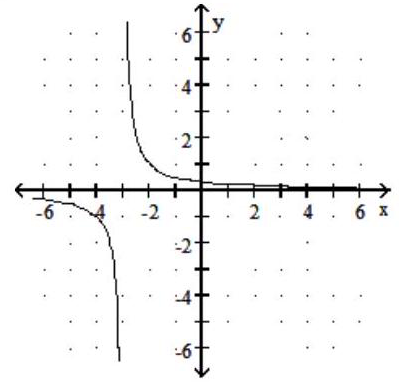
D)
-f(x) = + 3

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
10
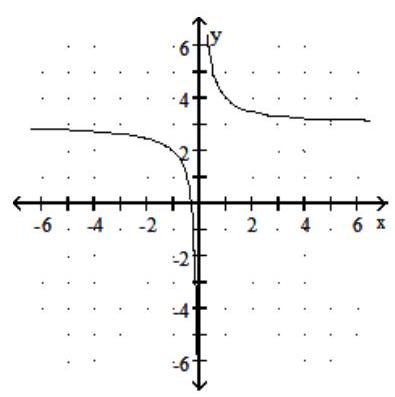
Graph the rational function.
-f(x) = + 3
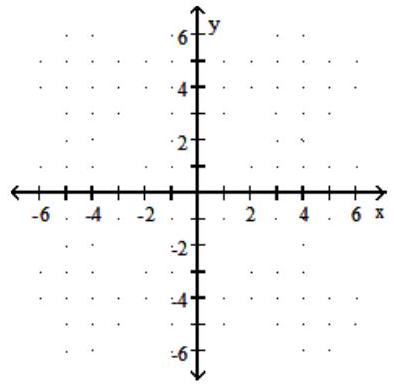
A)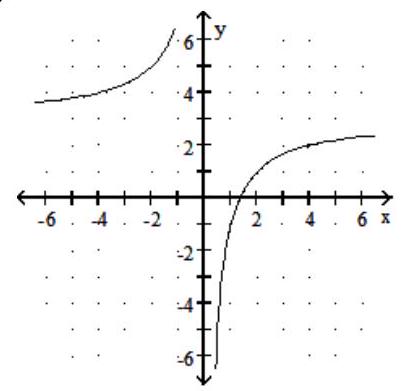
B)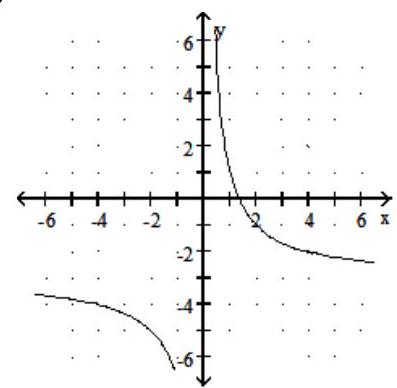
C)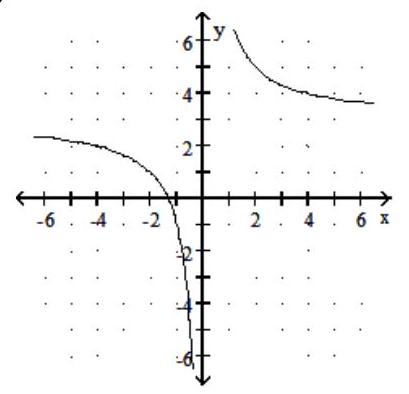
D)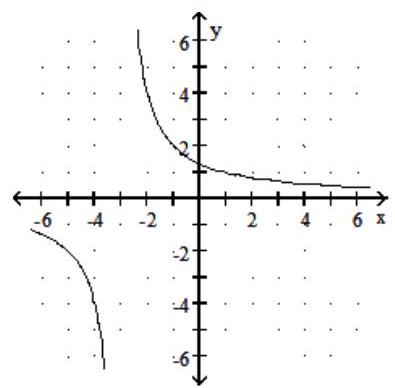
-f(x) = + 3

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
11
Graph the function.
-
A)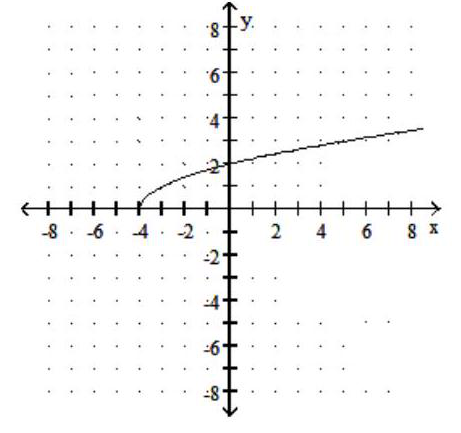
B)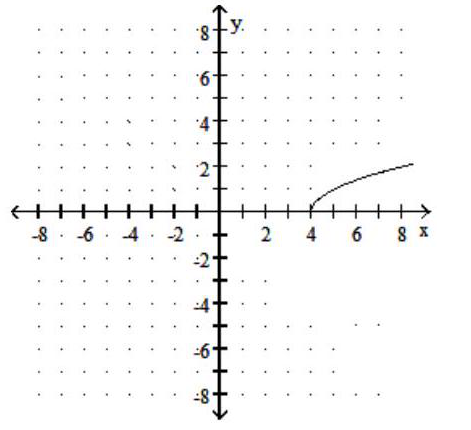
C)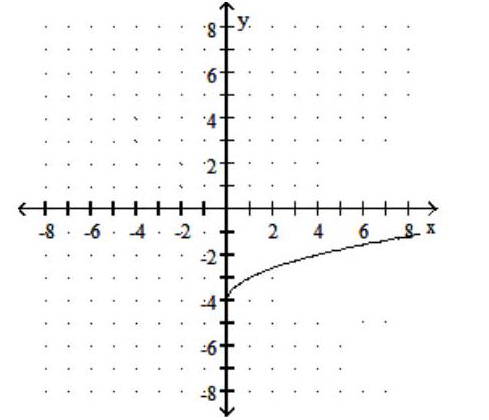
D)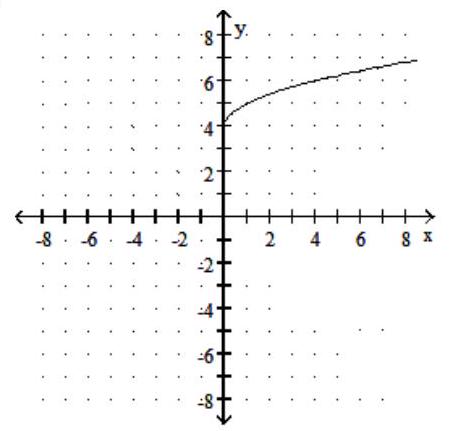
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
12
Graph the function.
-
A)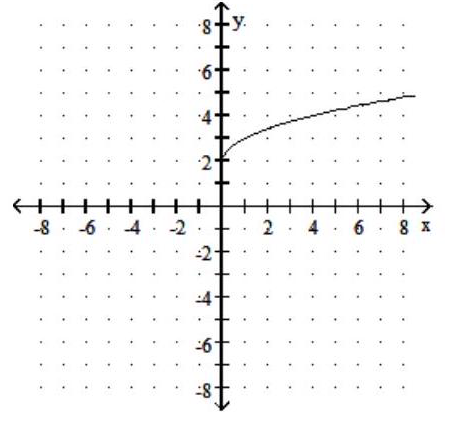
B)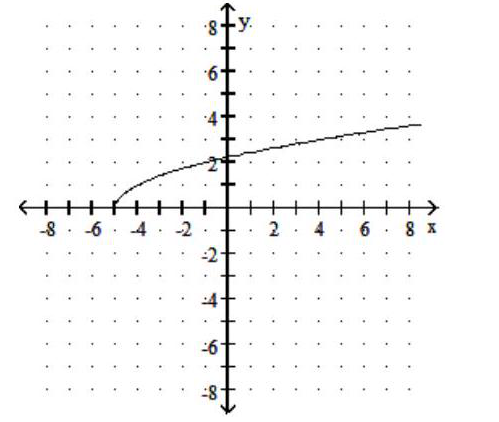
C)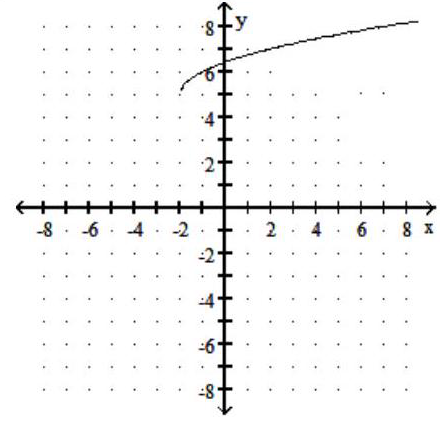
D)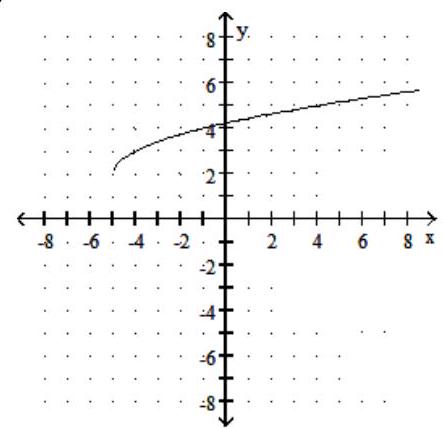
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
13
Graph the function. Give the domain and range.
-
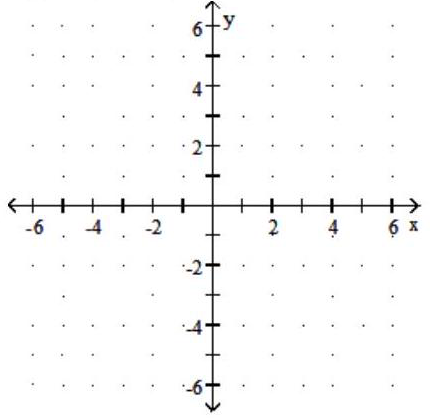
A) Domain: ; Range:
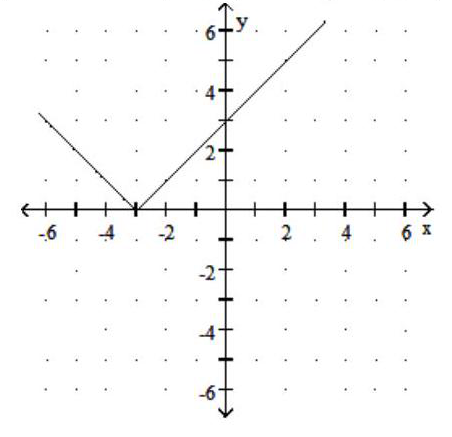
B) Domain: ; Range:
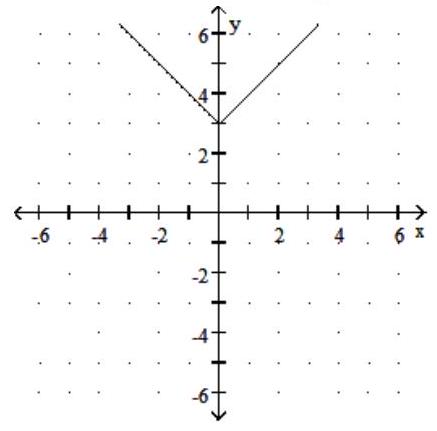
C) Domain: ; Range:
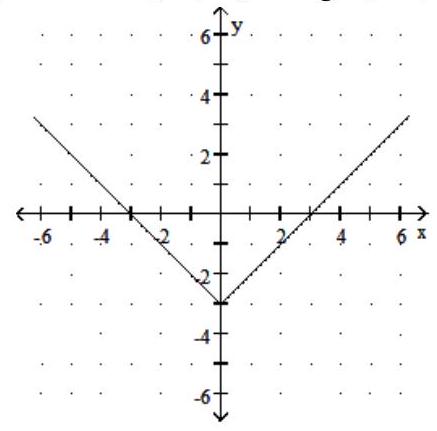
D) Domain: ; Range:
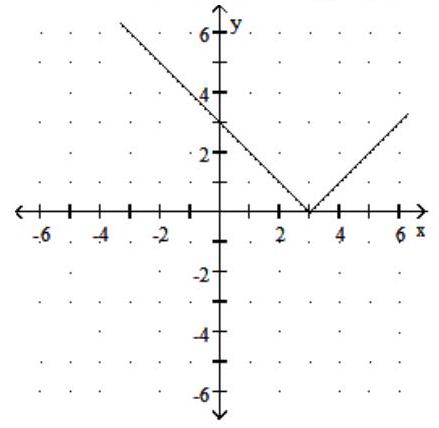
-

A) Domain: ; Range:

B) Domain: ; Range:

C) Domain: ; Range:

D) Domain: ; Range:


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
14
Graph the function. Give the domain and range.
-
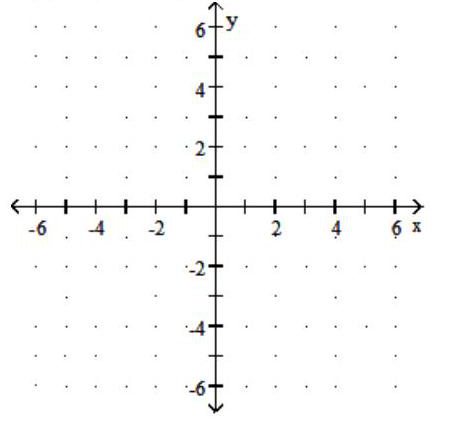
A) Domain: ; Range:
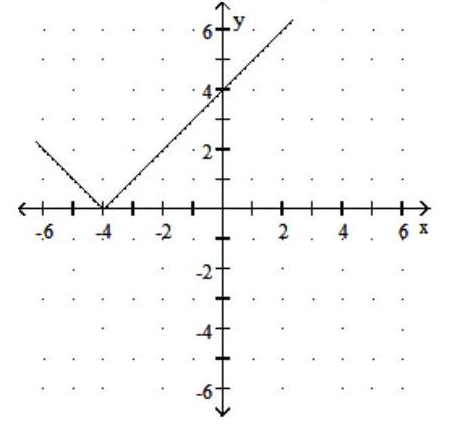
B) Domain: ; Range:
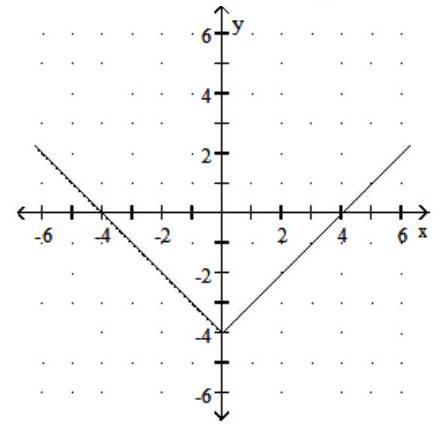
C) Domain: ; Range:
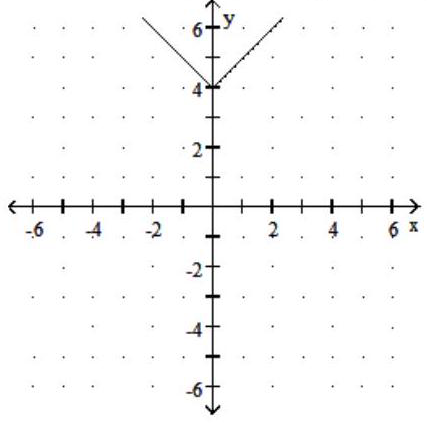
D) Domain: ; Range:
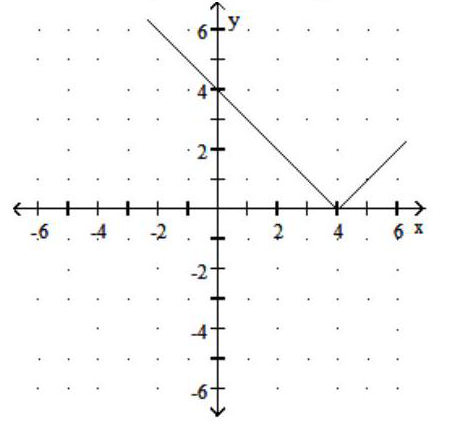
-

A) Domain: ; Range:

B) Domain: ; Range:

C) Domain: ; Range:

D) Domain: ; Range:


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
15
Graph the function. Give the domain and range.
-
A) Domain: ; Range:
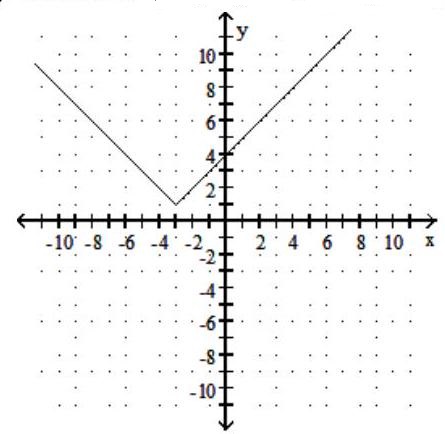
B) Domain: ; Range:
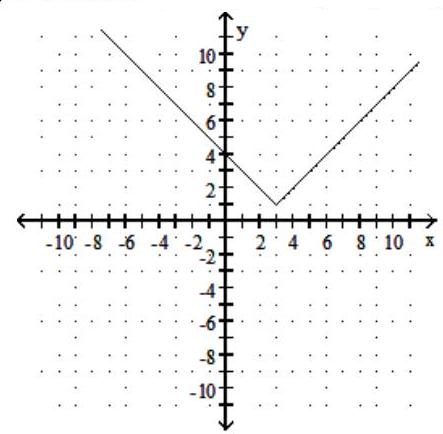
C) Domain: ; Range:
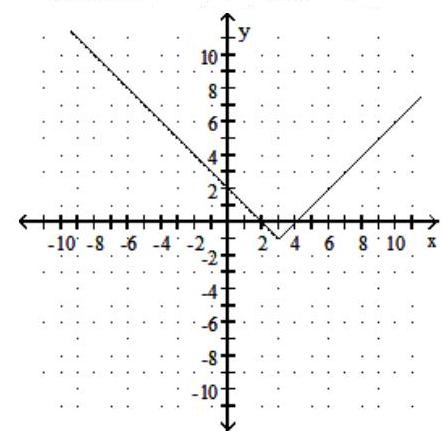
D) Domain: ; Range:
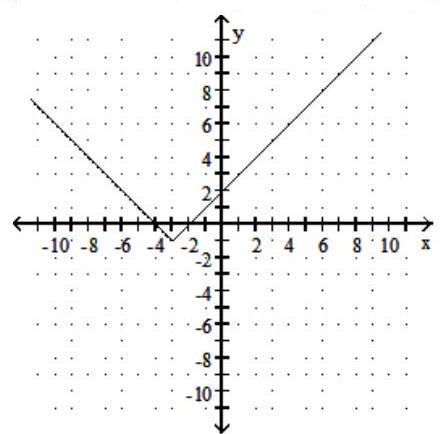
-

A) Domain: ; Range:

B) Domain: ; Range:

C) Domain: ; Range:

D) Domain: ; Range:


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
16
Graph the function. Give the domain and range.
-
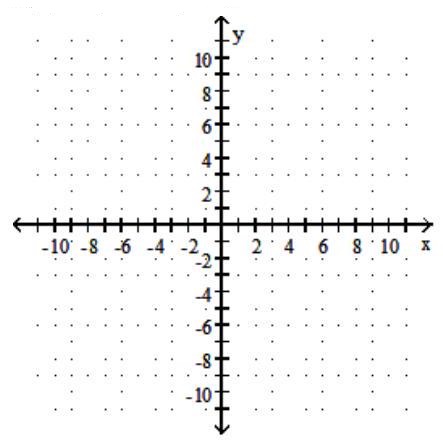
A) Domain: ; Range:
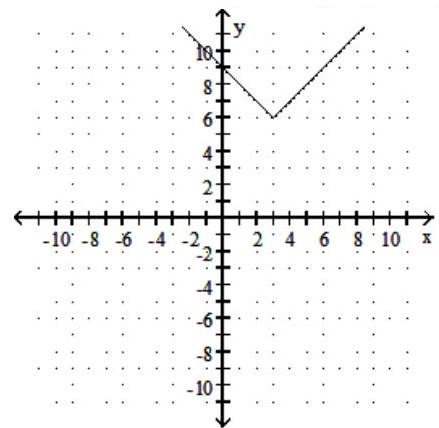
B) Domain: ; Range:
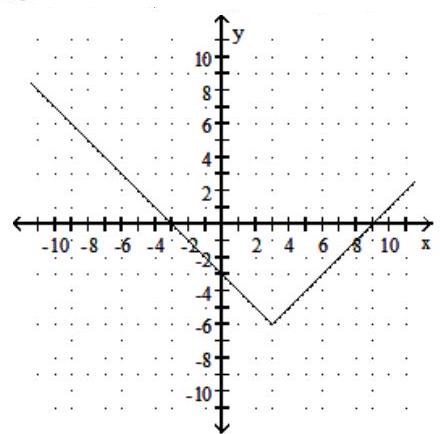
C) Domain: ; Range:
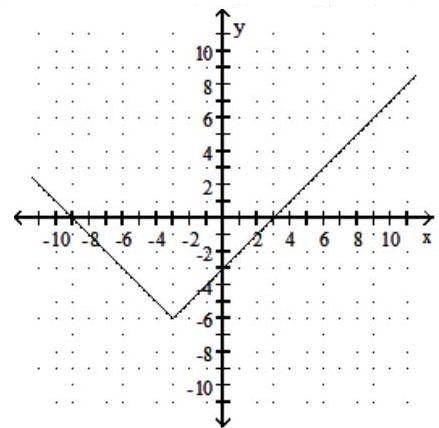
D) Domain: ; Range:
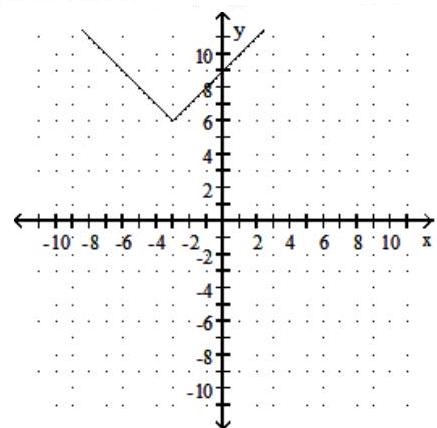
-

A) Domain: ; Range:

B) Domain: ; Range:

C) Domain: ; Range:

D) Domain: ; Range:


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
17
Evaluate the expression.
-
A) 4
B) -5
C) 5
D) 6
-
A) 4
B) -5
C) 5
D) 6

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
18
Evaluate the expression.
-
A) 7
B) 8
C) -7
D) 6
-
A) 7
B) 8
C) -7
D) 6

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
19
Evaluate the expression.
-[[-18]]
A) -17
B) -18
C) -19
D) 18
-[[-18]]
A) -17
B) -18
C) -19
D) 18

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
20
Evaluate the expression.
-
A) -19
B) -21
C) -20
D) -8
-
A) -19
B) -21
C) -20
D) -8

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
21
Evaluate the expression.
-
A) 1
B) 0
C)
D) 7
-
A) 1
B) 0
C)
D) 7

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
22
Graph the step function.
-
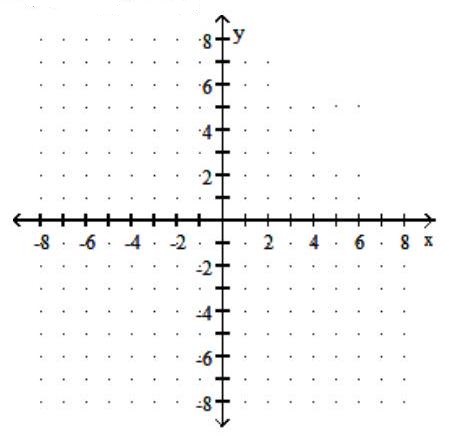
A)
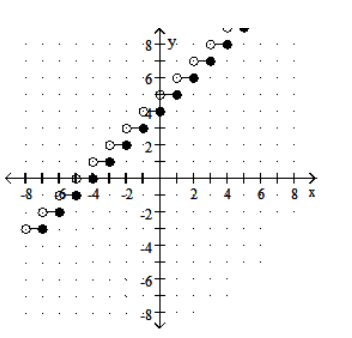
B)
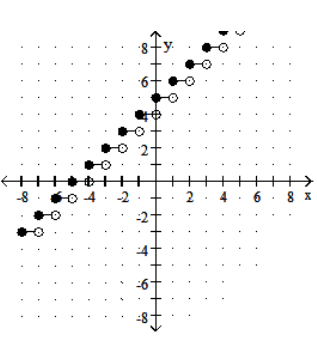
C)
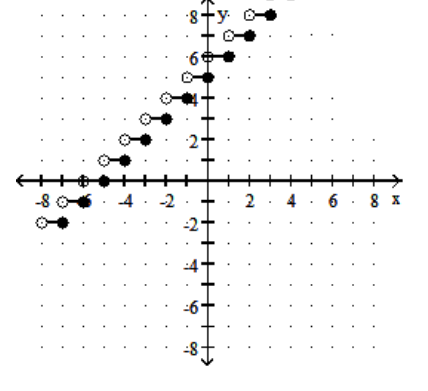
D)
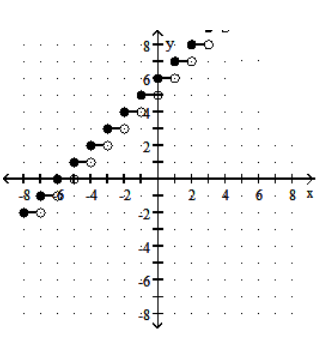
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
23
Graph the step function.
-
A)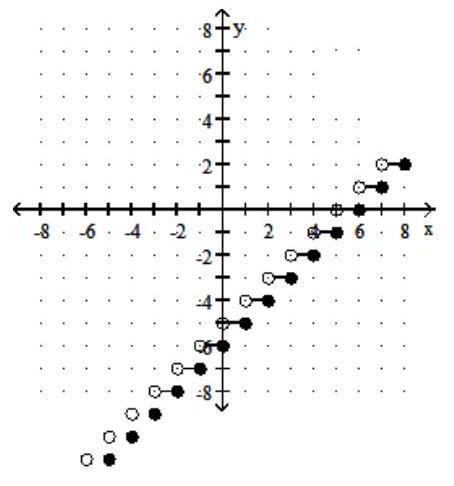
B)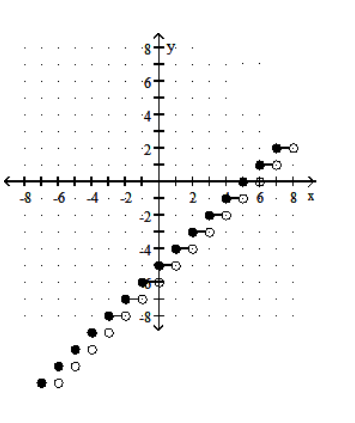
C)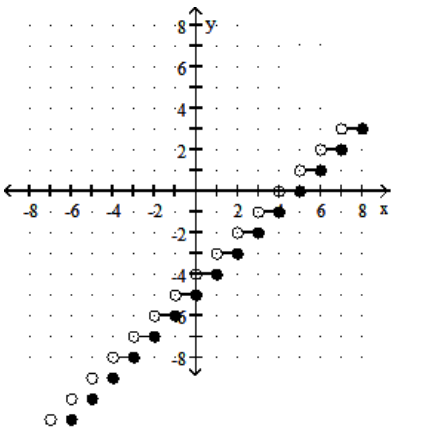
D)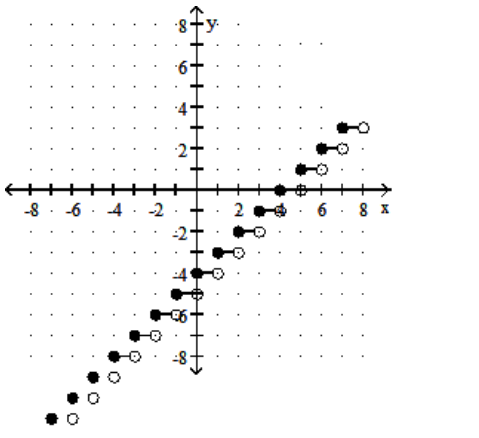
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
24
Graph the step function.
-Assume it costs 25 cents to mail a letter weighing one ounce or less, and then 20 cents for each additional ounce or fraction of an ounce. Let be the cost of mailing a letter weighing ounces. Graph . Use the interval .
A)
![<strong>Graph the step function. -Assume it costs 25 cents to mail a letter weighing one ounce or less, and then 20 cents for each additional ounce or fraction of an ounce. Let \mathrm{L}(\mathrm{x}) be the cost of mailing a letter weighing \mathrm{x} ounces. Graph y=L(x) . Use the interval (0,4] .</strong> A) B) C) D)](https://storage.examlex.com/TB10232/11eebf4d_ef0d_092c_8659_757472566cc5_TB10232_00.jpg)
B)
![<strong>Graph the step function. -Assume it costs 25 cents to mail a letter weighing one ounce or less, and then 20 cents for each additional ounce or fraction of an ounce. Let \mathrm{L}(\mathrm{x}) be the cost of mailing a letter weighing \mathrm{x} ounces. Graph y=L(x) . Use the interval (0,4] .</strong> A) B) C) D)](https://storage.examlex.com/TB10232/11eebf4d_ef0d_092d_8659_2dbe09d13802_TB10232_00.jpg)
C)
![<strong>Graph the step function. -Assume it costs 25 cents to mail a letter weighing one ounce or less, and then 20 cents for each additional ounce or fraction of an ounce. Let \mathrm{L}(\mathrm{x}) be the cost of mailing a letter weighing \mathrm{x} ounces. Graph y=L(x) . Use the interval (0,4] .</strong> A) B) C) D)](https://storage.examlex.com/TB10232/11eebf4d_ef0d_092e_8659_cf6230c7d8c4_TB10232_00.jpg)
D)
![<strong>Graph the step function. -Assume it costs 25 cents to mail a letter weighing one ounce or less, and then 20 cents for each additional ounce or fraction of an ounce. Let \mathrm{L}(\mathrm{x}) be the cost of mailing a letter weighing \mathrm{x} ounces. Graph y=L(x) . Use the interval (0,4] .</strong> A) B) C) D)](https://storage.examlex.com/TB10232/11eebf4d_ef0d_092f_8659_4bb8ad9a9c76_TB10232_00.jpg)
-Assume it costs 25 cents to mail a letter weighing one ounce or less, and then 20 cents for each additional ounce or fraction of an ounce. Let be the cost of mailing a letter weighing ounces. Graph . Use the interval .
A)
![<strong>Graph the step function. -Assume it costs 25 cents to mail a letter weighing one ounce or less, and then 20 cents for each additional ounce or fraction of an ounce. Let \mathrm{L}(\mathrm{x}) be the cost of mailing a letter weighing \mathrm{x} ounces. Graph y=L(x) . Use the interval (0,4] .</strong> A) B) C) D)](https://storage.examlex.com/TB10232/11eebf4d_ef0d_092c_8659_757472566cc5_TB10232_00.jpg)
B)
![<strong>Graph the step function. -Assume it costs 25 cents to mail a letter weighing one ounce or less, and then 20 cents for each additional ounce or fraction of an ounce. Let \mathrm{L}(\mathrm{x}) be the cost of mailing a letter weighing \mathrm{x} ounces. Graph y=L(x) . Use the interval (0,4] .</strong> A) B) C) D)](https://storage.examlex.com/TB10232/11eebf4d_ef0d_092d_8659_2dbe09d13802_TB10232_00.jpg)
C)
![<strong>Graph the step function. -Assume it costs 25 cents to mail a letter weighing one ounce or less, and then 20 cents for each additional ounce or fraction of an ounce. Let \mathrm{L}(\mathrm{x}) be the cost of mailing a letter weighing \mathrm{x} ounces. Graph y=L(x) . Use the interval (0,4] .</strong> A) B) C) D)](https://storage.examlex.com/TB10232/11eebf4d_ef0d_092e_8659_cf6230c7d8c4_TB10232_00.jpg)
D)
![<strong>Graph the step function. -Assume it costs 25 cents to mail a letter weighing one ounce or less, and then 20 cents for each additional ounce or fraction of an ounce. Let \mathrm{L}(\mathrm{x}) be the cost of mailing a letter weighing \mathrm{x} ounces. Graph y=L(x) . Use the interval (0,4] .</strong> A) B) C) D)](https://storage.examlex.com/TB10232/11eebf4d_ef0d_092f_8659_4bb8ad9a9c76_TB10232_00.jpg)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
25
The lowest point on the graph of has what coordinates?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
26
What is the domain of the square root function, given by ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
27
What is the domain of the greatest integer function, given by ?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
28
What is the only real number not in the domain of ?
A) -3
B)
C) 3
D) 0
A) -3
B)
C) 3
D) 0

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
29
Choose the equation that matches the graph.
-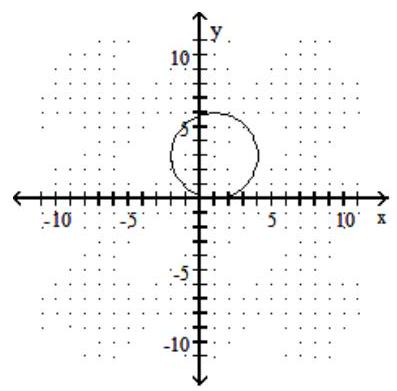
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
30
Choose the equation that matches the graph.
-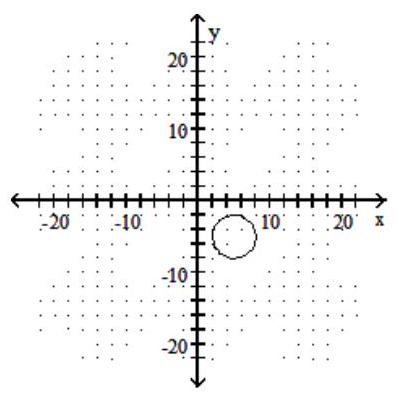
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
31
Find the equation of a circle satisfying the given conditions.
-Center: ; radius: 12
A)
B)
C)
D)
-Center: ; radius: 12
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
32
Find the equation of a circle satisfying the given conditions.
-Center: ; radius: 2
A)
B)
C)
D)
-Center: ; radius: 2
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
33
Find the equation of a circle satisfying the given conditions.
-Center: ; radius: 10
A)
B)
C)
D)
-Center: ; radius: 10
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
34
Find the equation of a circle satisfying the given conditions.
-Center: ; radius:
A)
B)
C)
D)
-Center: ; radius:
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
35
Find the equation of a circle satisfying the given conditions.
-Center: ; radius:
A)
B)
C)
D)
-Center: ; radius:
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
36
Find the center and radius of the circle.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
37
Find the center and radius of the circle.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
38
Find the center and radius of the circle.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
39
Graph the circle.
-
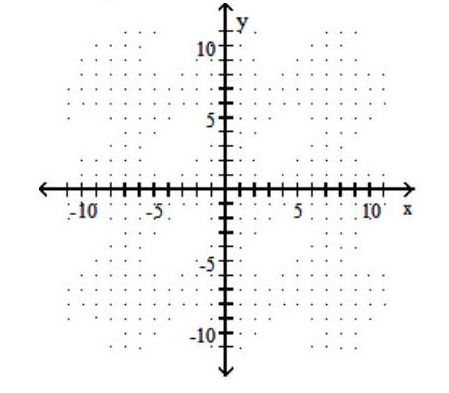
A)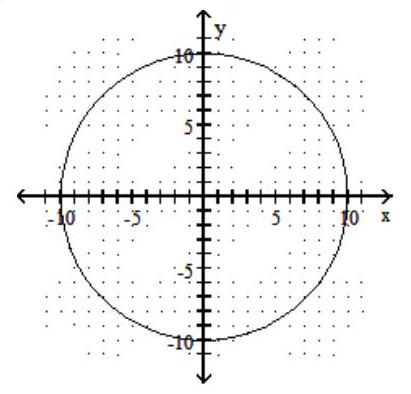
B)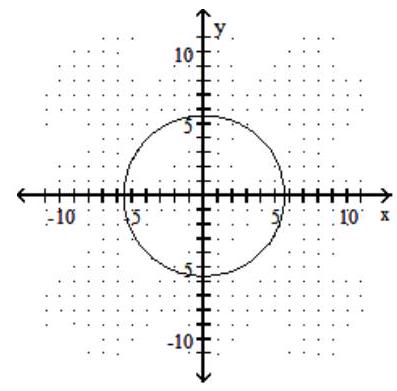
C)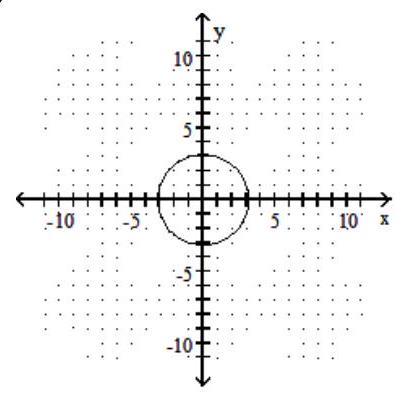
D)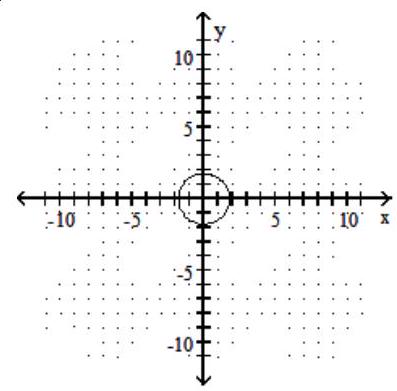
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
40
Graph the circle.
-
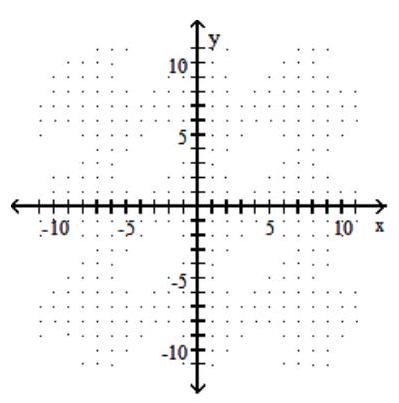
A)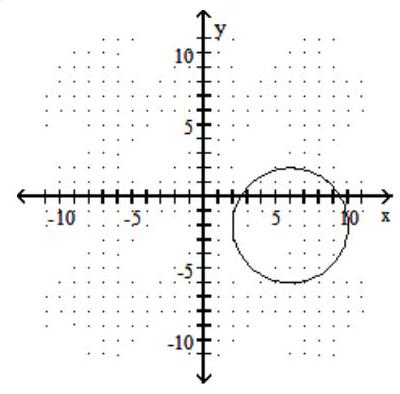
B)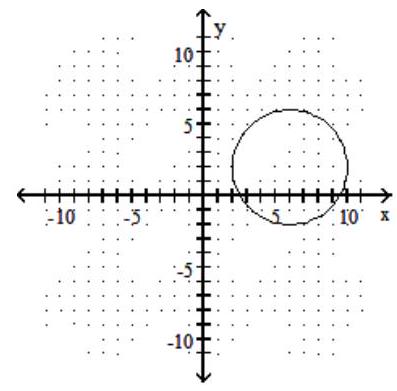
C)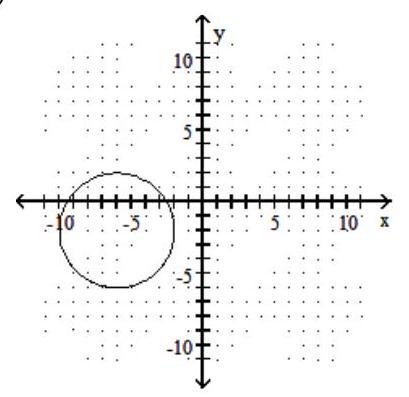
D)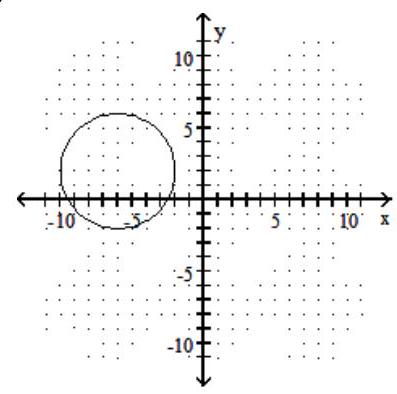
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
41
Graph the circle.
-
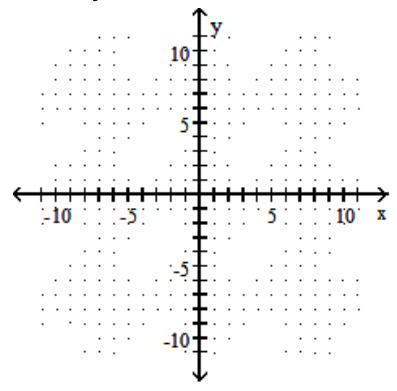
A)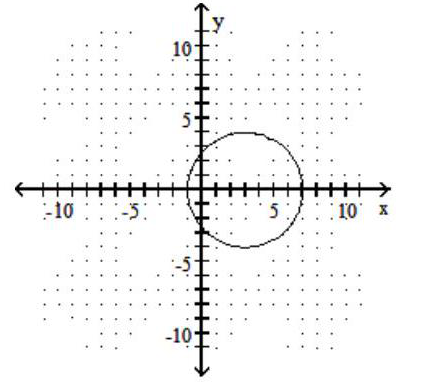
B)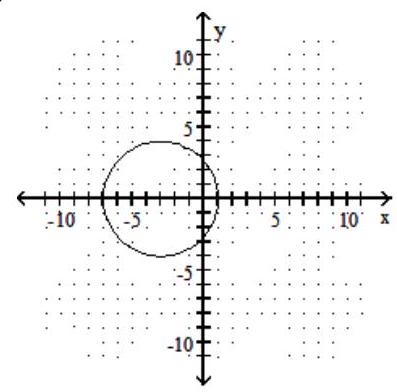
C)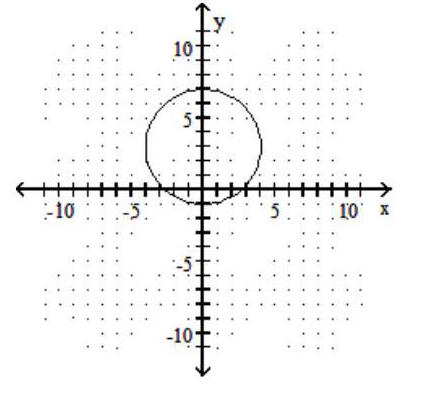
D)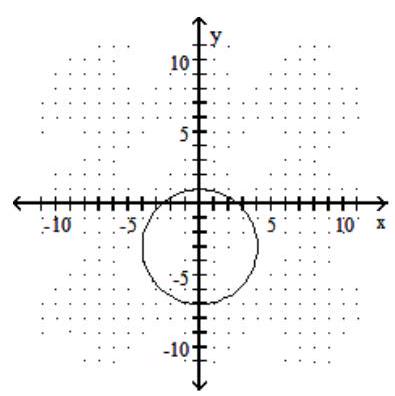
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
42
Graph the circle.
-
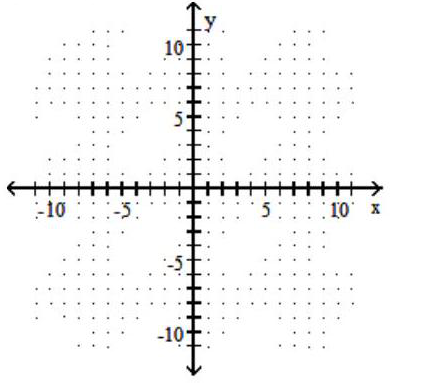
A)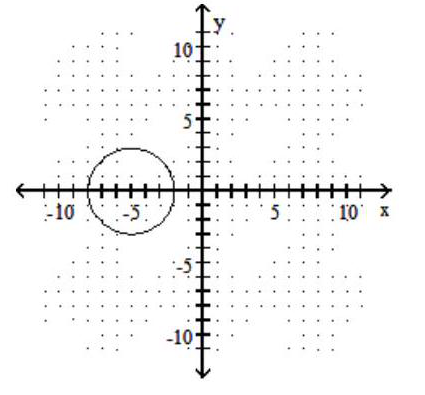
B)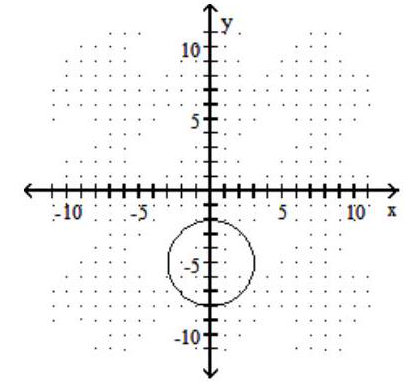
C)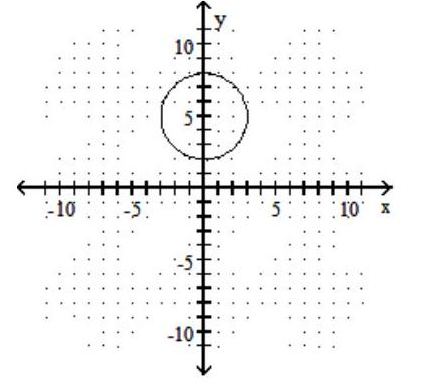
D)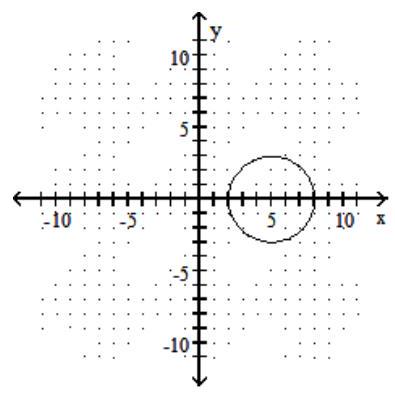
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
43
Graph the circle.
-
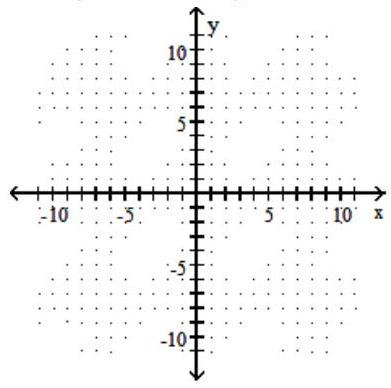
A)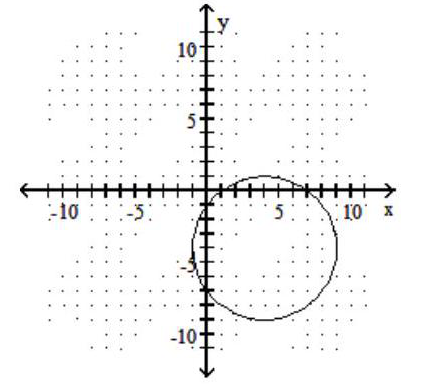
B)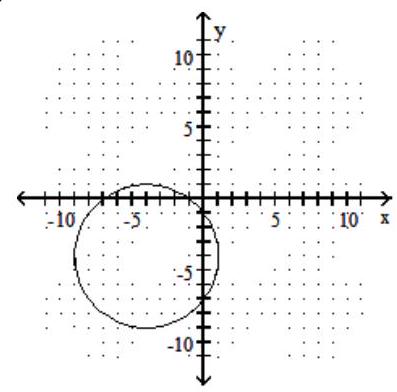
C)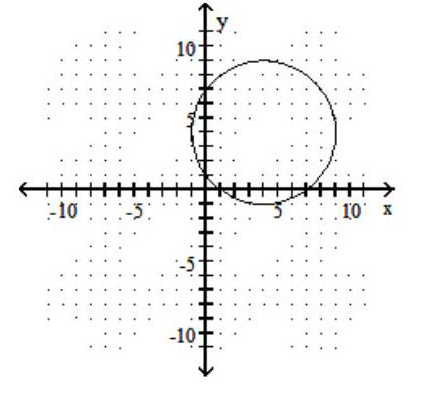
D)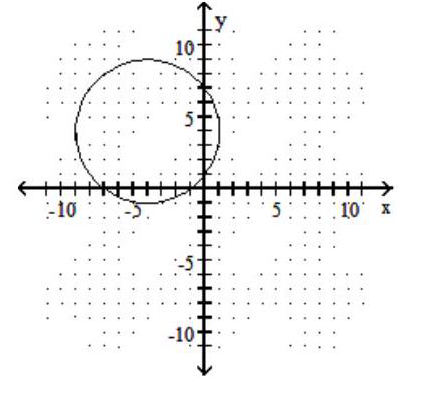
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
44
Graph the circle.
-
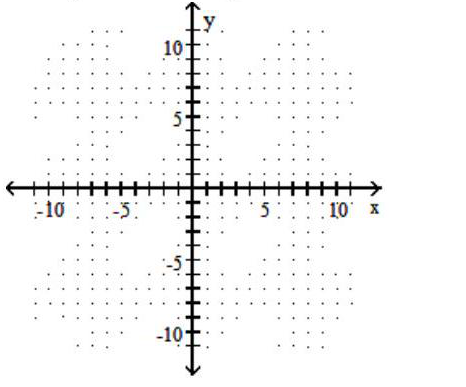
A)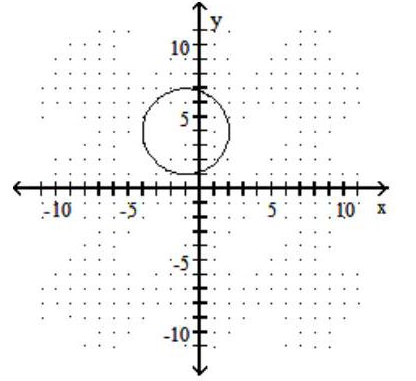
B)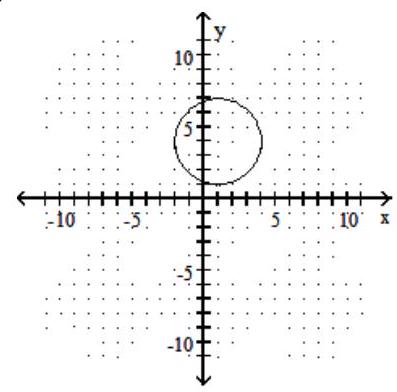
C)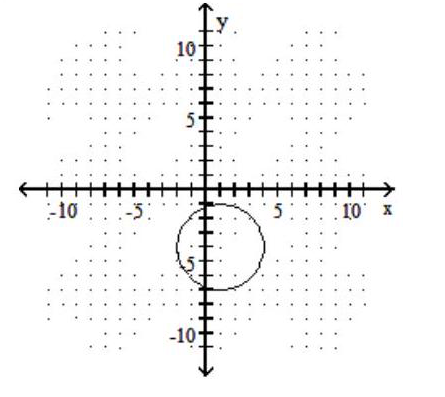
D)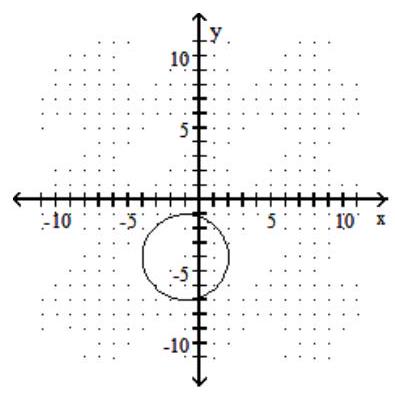
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
45
Graph the circle.
-
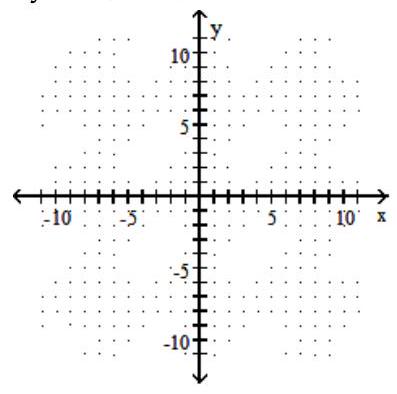
A)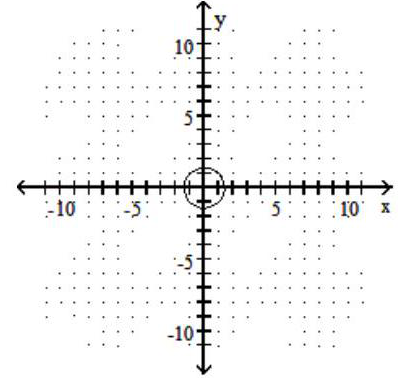
B)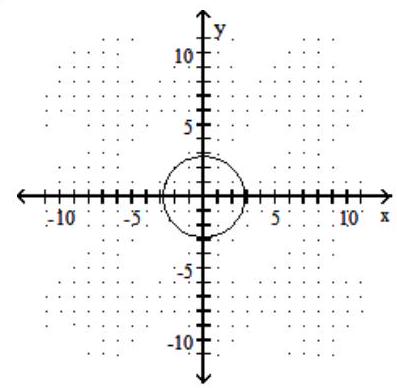
C)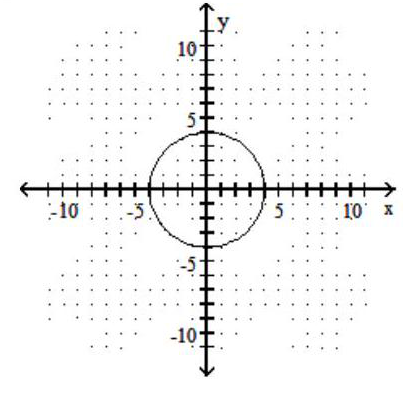
D)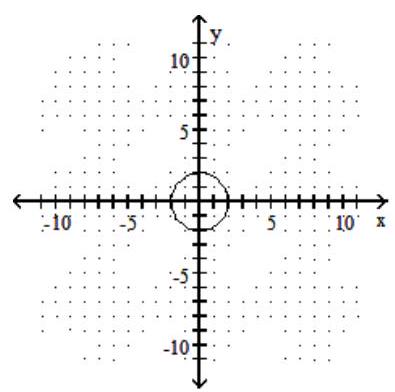
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
46
Graph the ellipse.
-
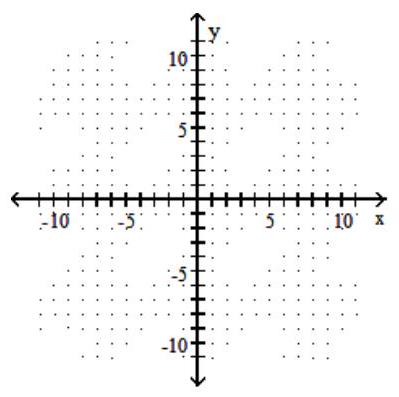
A)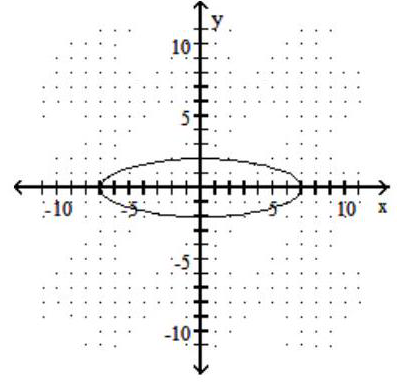
B)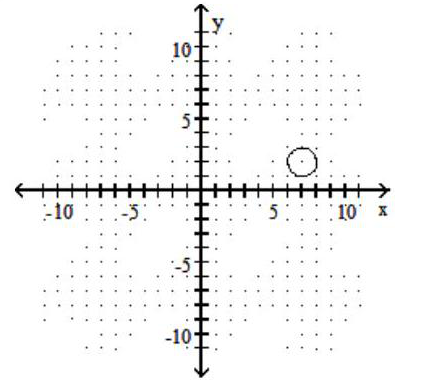
C)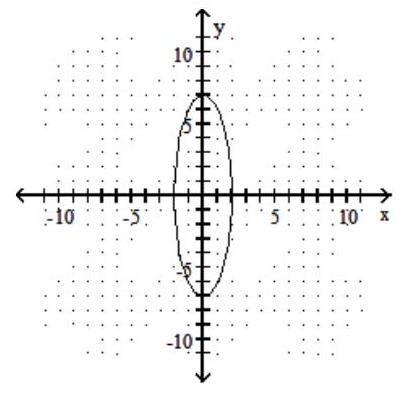
D)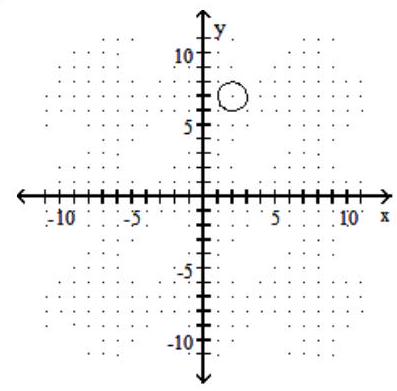
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
47
Graph the ellipse.
-
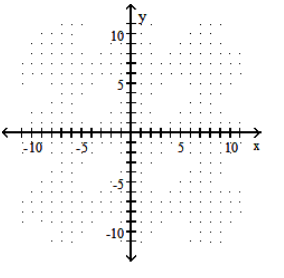
A)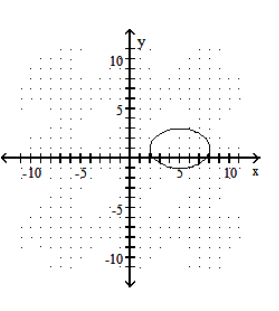
B)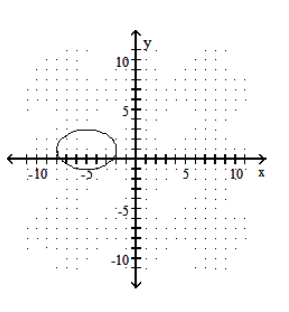
C)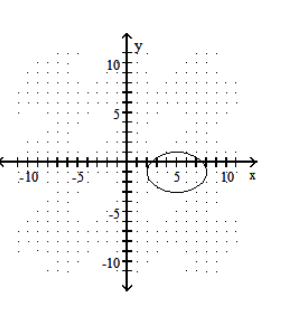
D)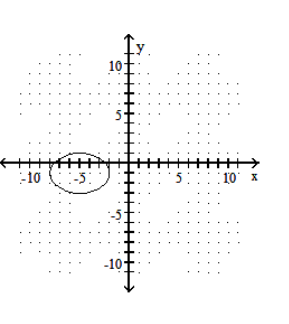
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
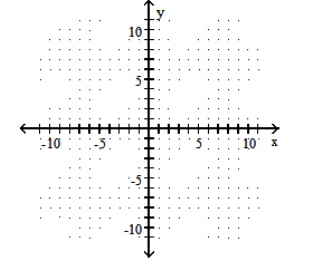
48
Graph the ellipse.
-
A)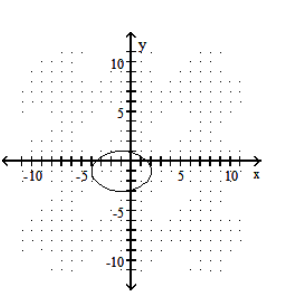
B)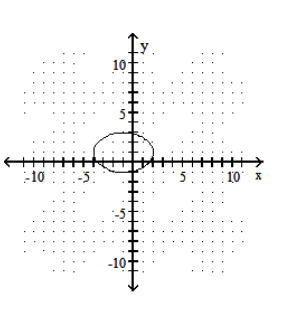
C)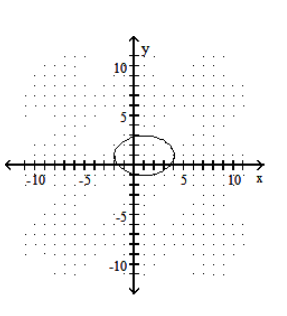
D)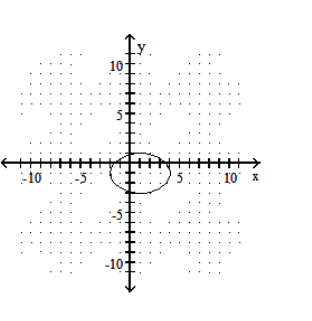
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
49
The circle or ellipse shown in the calculator-generated graph was created using function mode with a square viewing window. What are the two functions and that were used to obtain the graph whose equation is given?
-
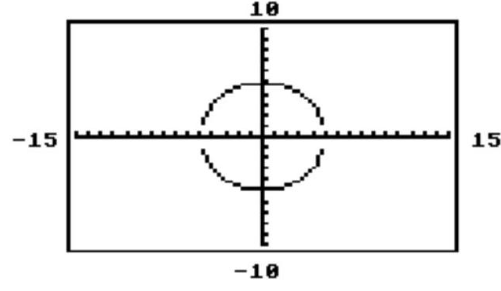
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
50
The circle or ellipse shown in the calculator-generated graph was created using function mode with a square viewing window. What are the two functions and that were used to obtain the graph whose equation is given?
-
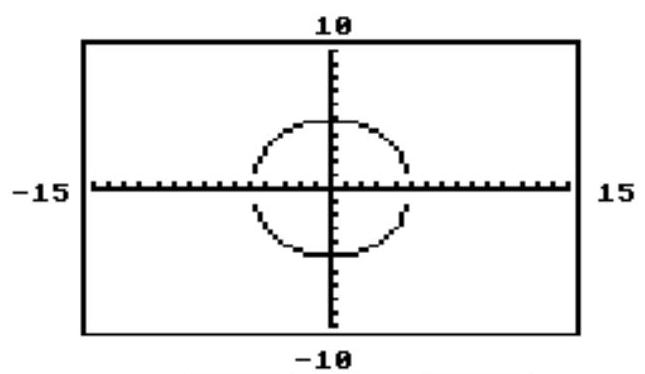
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
51
The circle or ellipse shown in the calculator-generated graph was created using function mode with a square viewing window. What are the two functions and that were used to obtain the graph whose equation is given?
-
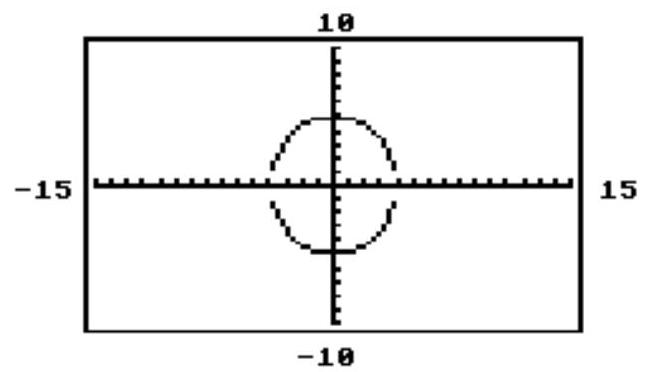
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
52
The circle or ellipse shown in the calculator-generated graph was created using function mode with a square viewing window. What are the two functions and that were used to obtain the graph whose equation is given?
-
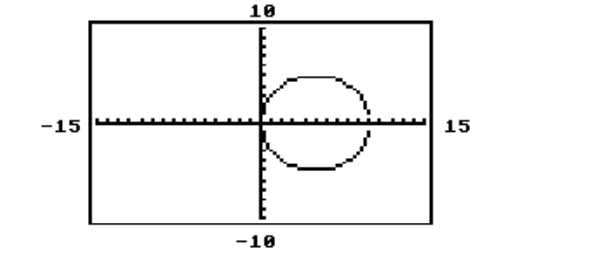
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
53
The circle or ellipse shown in the calculator-generated graph was created using function mode with a square viewing window. What are the two functions and that were used to obtain the graph whose equation is given?
-
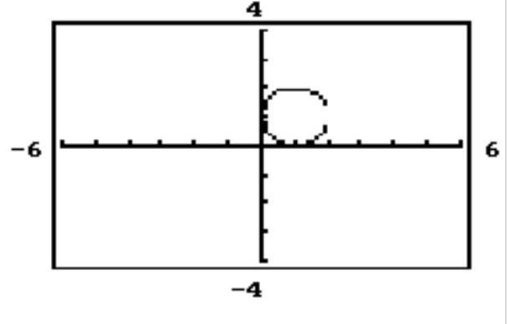
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
54
The circle or ellipse shown in the calculator-generated graph was created using function mode with a square viewing window. What are the two functions and that were used to obtain the graph whose equation is given?
-
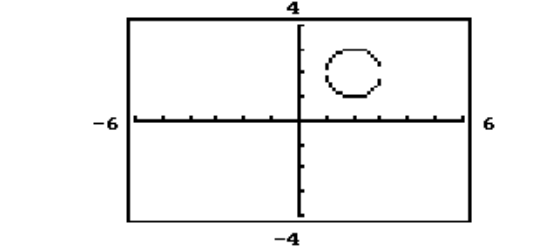
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
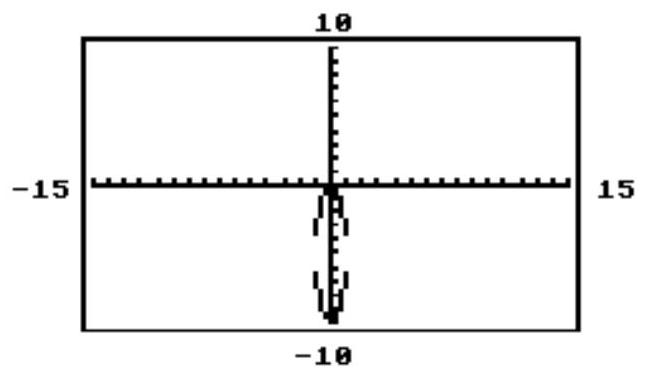
55
The circle or ellipse shown in the calculator-generated graph was created using function mode with a square viewing window. What are the two functions and that were used to obtain the graph whose equation is given?
-
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
56
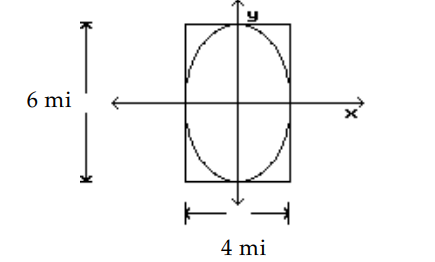
Solve the problem.
-An elliptical riding path is to be built on a rectangular piece of property that measures by . Find an equation for the ellipse, where and are measured in , if the path is to touch the center of the property line on all 4 sides.
A)
B)
C)
D)
-An elliptical riding path is to be built on a rectangular piece of property that measures by . Find an equation for the ellipse, where and are measured in , if the path is to touch the center of the property line on all 4 sides.

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
57
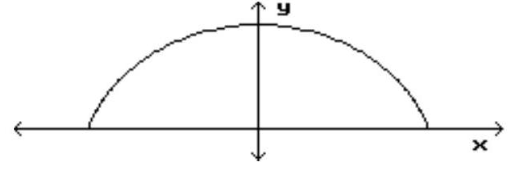
Solve the problem.
-A railroad tunnel has the shape of half an ellipse. The height of the tunnel at the center is and the vertical clearance must be at a point from the center. Find an equation for the ellipse, where and are measured in .
A)
B)
C)
D)
-A railroad tunnel has the shape of half an ellipse. The height of the tunnel at the center is and the vertical clearance must be at a point from the center. Find an equation for the ellipse, where and are measured in .

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
58
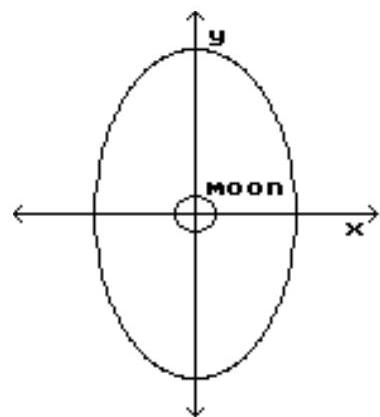
Solve the problem.
-A satellite is to be put into an elliptical orbit around a moon. The moon is a sphere with radius 589 . Determine an equation for the ellipse, where and are measured in , if the distance of the satellite from the surface of the moon varies from to .
A)
B)
C)
D)
-A satellite is to be put into an elliptical orbit around a moon. The moon is a sphere with radius 589 . Determine an equation for the ellipse, where and are measured in , if the distance of the satellite from the surface of the moon varies from to .

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
59
Solve the problem.
-A rectangular board is 8 by 20 . How far from the center of the board will the foci be located to determine the largest elliptical tabletop? Round your answer to the nearest tenth.
A) 9.2
B) .8
C) 4.0
D) 6.0
-A rectangular board is 8 by 20 . How far from the center of the board will the foci be located to determine the largest elliptical tabletop? Round your answer to the nearest tenth.
A) 9.2
B) .8
C) 4.0
D) 6.0

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
60
Solve the problem.
-A rectangular board is 8 by 14 . The foci of an ellipse are located to produce the largest area. A string is connected to the foci and pulled taut by a pencil in order to draw the ellipse. Find the length of the string.
A) 16
B) 8
C) 28
D) 14
-A rectangular board is 8 by 14 . The foci of an ellipse are located to produce the largest area. A string is connected to the foci and pulled taut by a pencil in order to draw the ellipse. Find the length of the string.
A) 16
B) 8
C) 28
D) 14

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
61
The circle with equation has center at .

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
62
The circle with equation has center at .

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
63
The equation of a circle centered at the origin with radius 5 is .

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
64
The equation of a semicircle that is the upper half of the circle centered at the origin with radius 2 is .

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
65
The -intercepts of the ellipse with equation are and .

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
66
The -intercepts of the ellipse with equation are and .

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
67
The -intercepts of the ellipse with equation are and .

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
68
The graph of the equation is an ellipse.

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
69
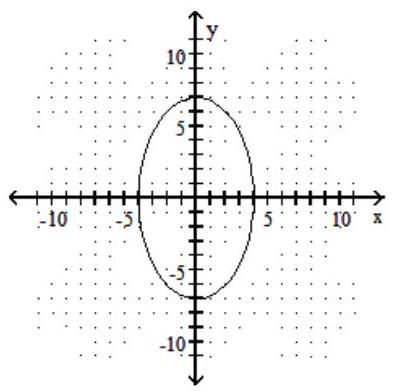
Choose the equation that matches the graph.
-
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
70
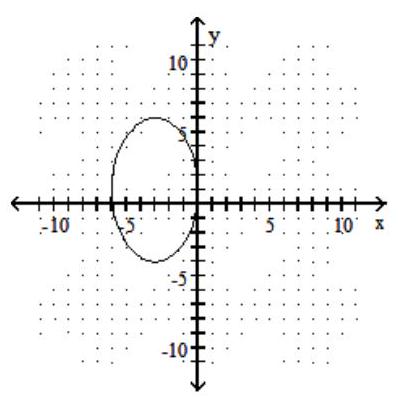
Choose the equation that matches the graph.
-
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
71
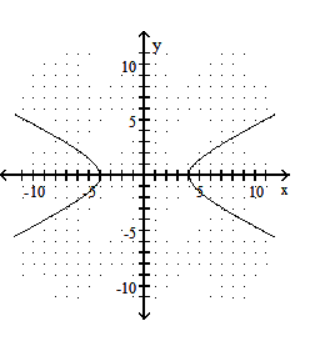
Choose the equation that matches the graph.
-
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
72
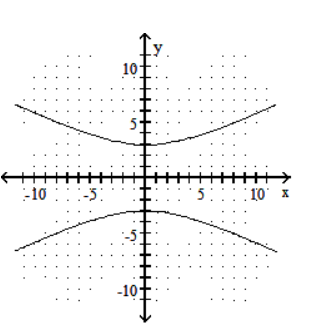
Choose the equation that matches the graph.
-
A)
B)
C)
D)
-

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
73
Graph the hyperbola.
-
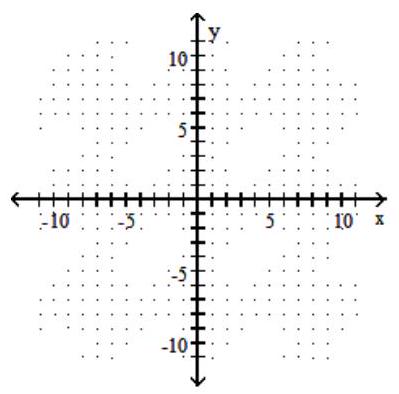
A)
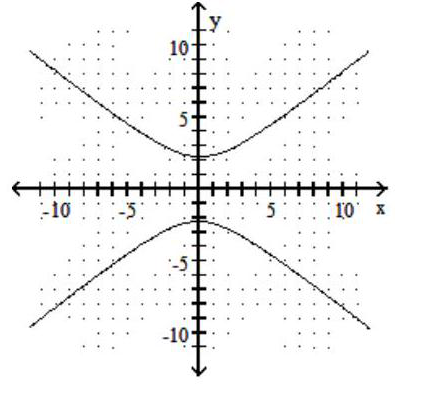
B)
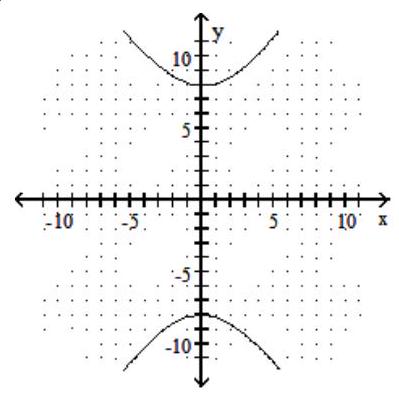
C)
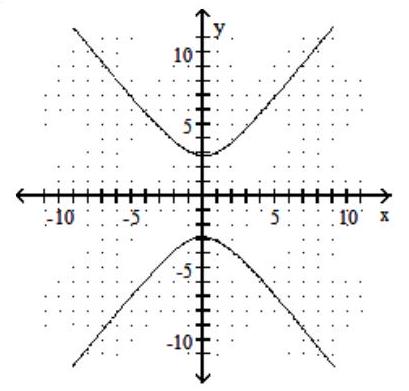
D)
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
74
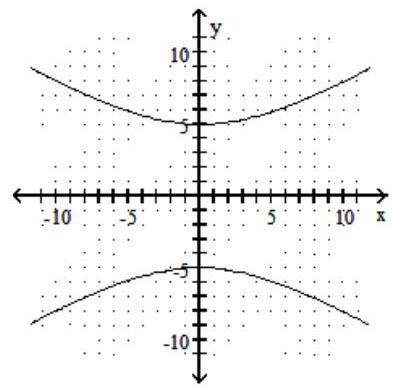
Graph the hyperbola.
-
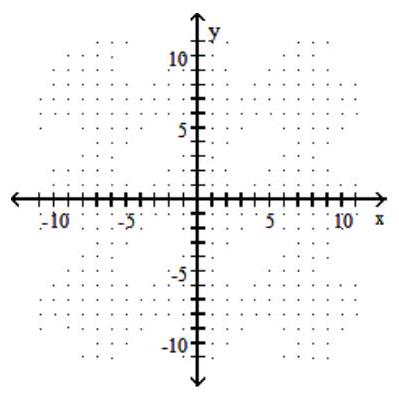
A)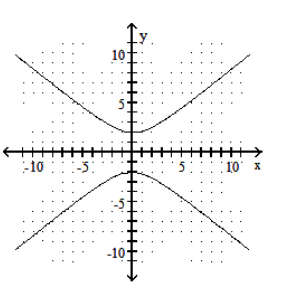
B)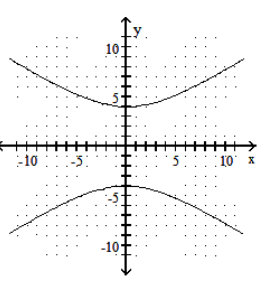
C)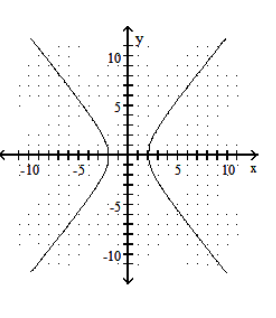
D)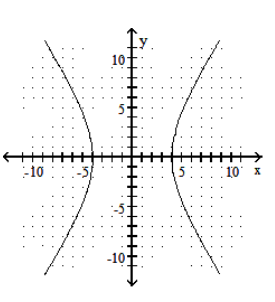
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
75
Graph the hyperbola.
-
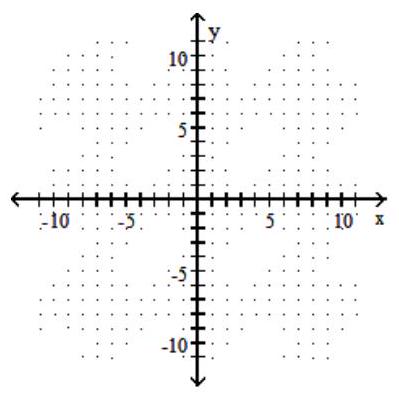
A)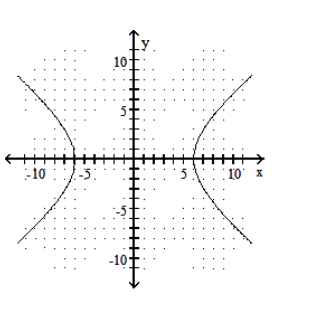
B)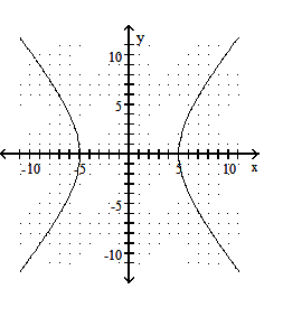
C)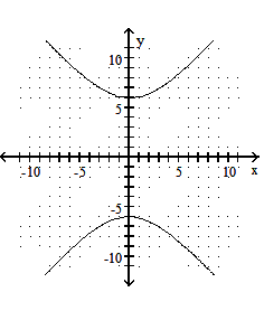
D)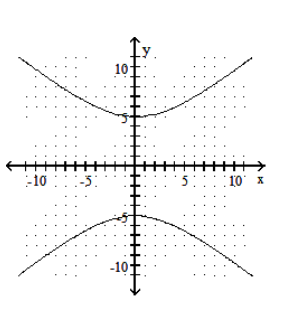
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
76
Graph the hyperbola.
-
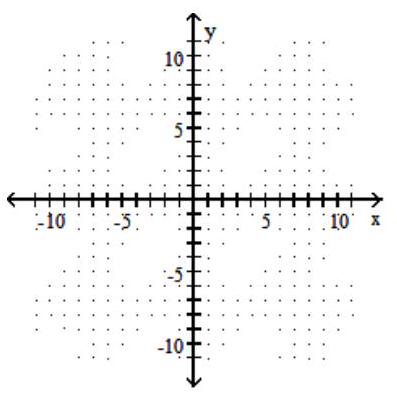
A)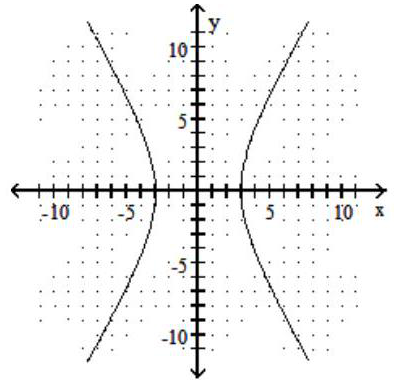
B)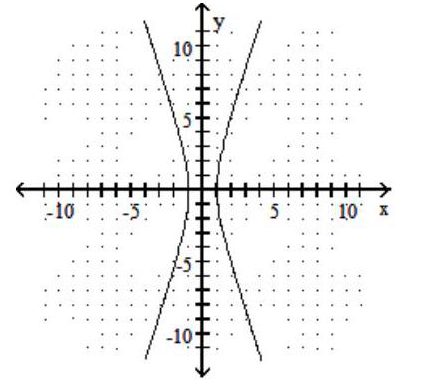
C)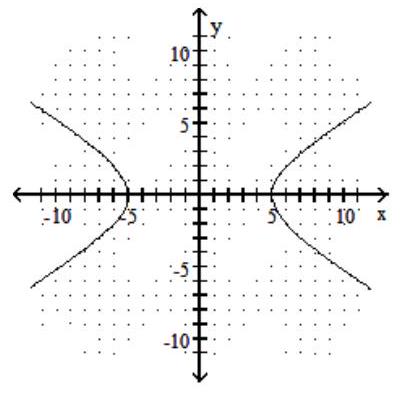
D)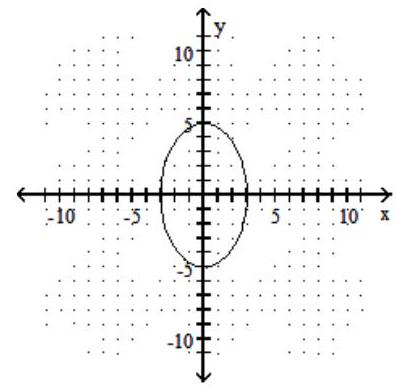
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
77
Graph the hyperbola.
-
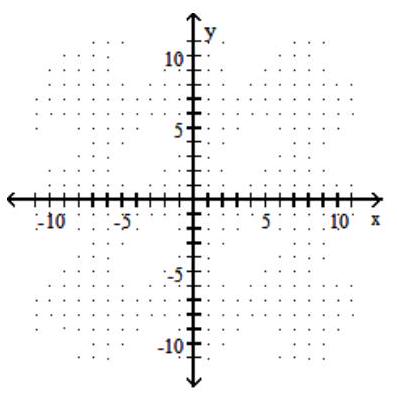
A)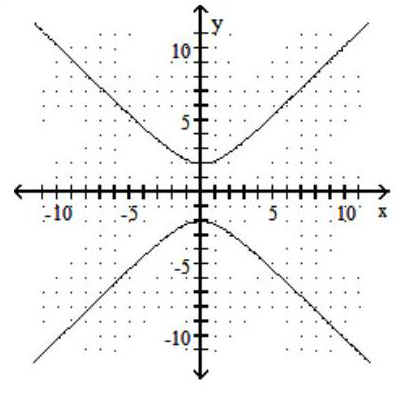
B)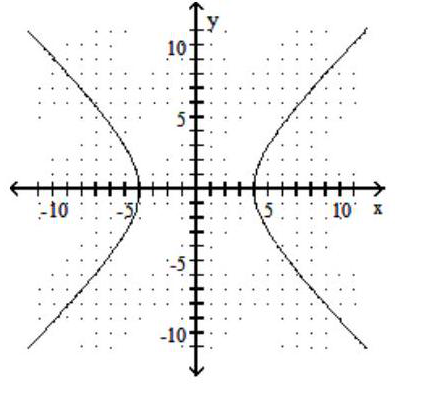
C)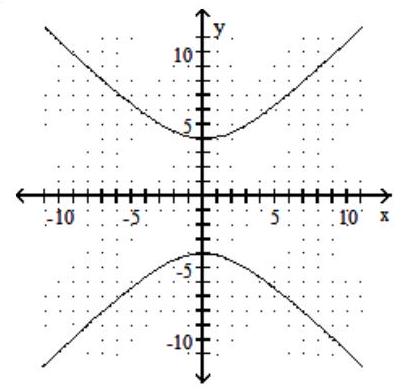
D)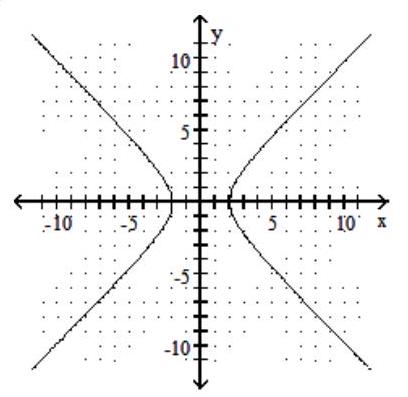
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
78
Graph the hyperbola.
-
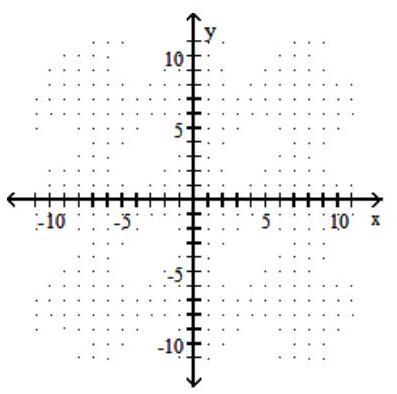
A)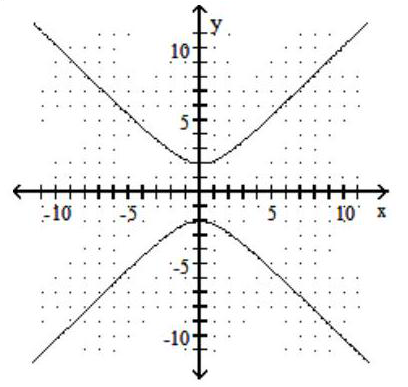
B)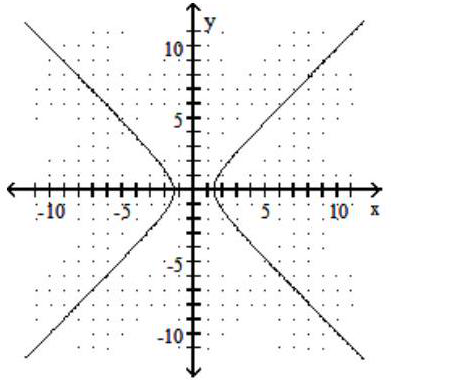
C)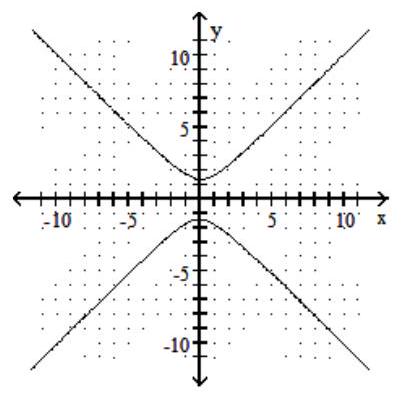
D)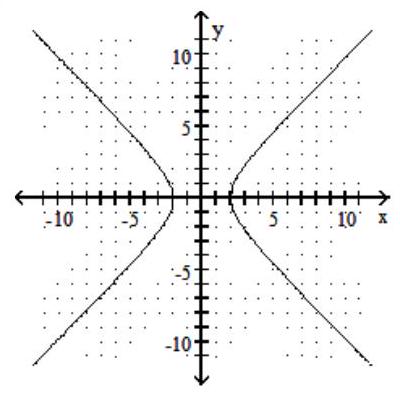
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
79
Identify the graph of the equation as a parabola, circle, ellipse, or hyperbola.
-
A) Parabola
B) Hyperbola
C) Circle
D) Ellipse
-
A) Parabola
B) Hyperbola
C) Circle
D) Ellipse

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck
80
Identify the graph of the equation as a parabola, circle, ellipse, or hyperbola.
-
A) Hyperbola
B) Ellipse
C) Circle
D) Parabola
-
A) Hyperbola
B) Ellipse
C) Circle
D) Parabola

Unlock Deck
Unlock for access to all 233 flashcards in this deck.
Unlock Deck
k this deck


