Deck 12: Further Topics in Algebra
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/190
Play
Full screen (f)
Deck 12: Further Topics in Algebra
1
Write out the first five terms of the sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)
2
Write out the first five terms of the sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)
3
Write out the first five terms of the sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)
4
Write out the first five terms of the sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
5
Write out the first five terms of the sequence.
-
A)
B)
C)
D) 1, 1, 1, 1, 1
-
A)
B)
C)
D) 1, 1, 1, 1, 1

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
6
Write out the first five terms of the sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
7
Write out the first five terms of the sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
8
Write out the first five terms of the sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
9
Write out the first five terms of the sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
10
Find the indicated term for the sequence.
- ;
A) 124
B) 128
C) 112
D) 136
- ;
A) 124
B) 128
C) 112
D) 136

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
11
Find the indicated term for the sequence.
-
A) 32
B) 33
C) 24
D) 31
-
A) 32
B) 33
C) 24
D) 31

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
12
Find the indicated term for the sequence.
- ; ag
A) -72
B) 72
C) 90
D) 9
- ; ag
A) -72
B) 72
C) 90
D) 9

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
13
Find the indicated term for the sequence.
- ;
A) 64
B) 12
C) 16
D) 81
- ;
A) 64
B) 12
C) 16
D) 81

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
14
Find the indicated term for the sequence.
-
A) 616
B) 384
C) 494
D) 750
-
A) 616
B) 384
C) 494
D) 750

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
15
Find the indicated term for the sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
16
Find a general term, , for the given terms of the sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
17
Find a general term, , for the given terms of the sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
18
Find a general term, , for the given terms of the sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
19
Find a general term, , for the given terms of the sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
20
Find a general term, , for the given terms of the sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
21
Find a general term, , for the given terms of the sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
22
Find a general term, , for the given terms of the sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
23
A man earned the first year he worked. If he received a raise of at the end of each year, what was his salary during the 15 th year?
A)
B)
C)
D) None of the above
A)
B)
C)
D) None of the above

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
24
The population of a town was 27,000 at the beginning of 1970 . If the population decreased 300 people per year, how many people lived in the town at the beginning of 1985 ?
A) 4500
B) 22,800
C) 22,200
D) 22,500
A) 4500
B) 22,800
C) 22,200
D) 22,500

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
25
An investment is worth , and its value is increasing by every year. What will its value be at the end of 9 years? Round your answer to the nearest dollar.
A)
B)
C)
D) \$1993
A)
B)
C)
D) \$1993

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
26
An investment is worth , and its value is increasing by every year. What will its value be at the end of 4 years? Round your answer to the nearest dollar.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
27
Evaluate the series
-
A) 8
B) 7
C) 9
D) 5
-
A) 8
B) 7
C) 9
D) 5

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
28
Evaluate the series
-
A) 42
B) 17
C) 54
D) 38
-
A) 42
B) 17
C) 54
D) 38

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
29
Evaluate the series
-
A) 243
B) 12
C) 120
D) 81
-
A) 243
B) 12
C) 120
D) 81

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
30
Evaluate the series
-
A) 39
B) 40
C) 78
D) 21
-
A) 39
B) 40
C) 78
D) 21

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
31
Evaluate the series
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
32
Evaluate the series
-
A) -22
B) -2
C) -18
D) 23
-
A) -22
B) -2
C) -18
D) 23

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
33
Write out the terms of the series.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
34
Write out the terms of the series.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
35
Write out the terms of the series.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
36
Write out the terms of the series.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
37
Write the series with summation notation.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
38
Write the series with summation notation.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
39
Write the series with summation notation.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
40
Find the arithmetic mean for the collection of numbers.
A) 51
B) 10
C) 9
D) 12.5
A) 51
B) 10
C) 9
D) 12.5

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
41
Find the arithmetic mean for the collection of numbers.
A) 9
B) 13
C) 10
D) 11
A) 9
B) 13
C) 10
D) 11

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
42
Find the arithmetic mean for the collection of numbers.
A) 13
B) 7.5
C) 4
D) 6
A) 13
B) 7.5
C) 4
D) 6

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
43
Find the arithmetic mean for the collection of numbers.
A)
B)
C)
D) 10
A)
B)
C)
D) 10

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
44
The number of mutual funds available to investors in Dereguland for each year during the period is given in the following table.
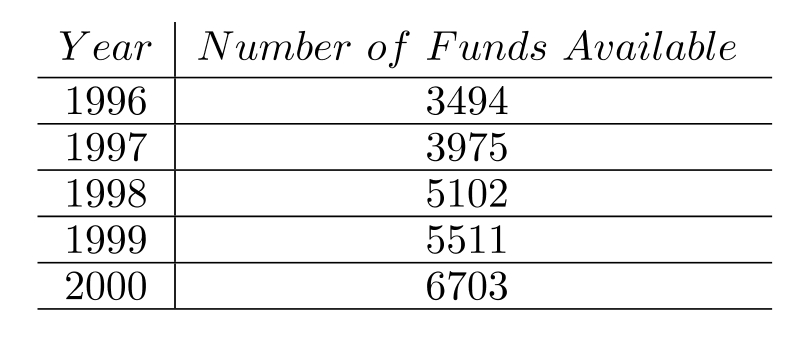
To the nearest whole number, what was the average number of funds available during this period?
A) 5102
B) 5099
C) 12,393
D) 4957

To the nearest whole number, what was the average number of funds available during this period?
A) 5102
B) 5099
C) 12,393
D) 4957

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
45
If the sequence is arithmetic, find the common difference. If the sequence is not arithmetic, say so.
-
A) 1.5
B) 2
C) 7
D) Not arithmetic
-
A) 1.5
B) 2
C) 7
D) Not arithmetic

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
46
If the sequence is arithmetic, find the common difference. If the sequence is not arithmetic, say so.
-
A) -1
B) 3
C) 1
D) Not arithmetic
-
A) -1
B) 3
C) 1
D) Not arithmetic

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
47
If the sequence is arithmetic, find the common difference. If the sequence is not arithmetic, say so.
-
A) -4
B) -6
C) -2
D) Not arithmetic
-
A) -4
B) -6
C) -2
D) Not arithmetic

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
48
If the sequence is arithmetic, find the common difference. If the sequence is not arithmetic, say so.
-
A) 2.86
B) 2.145
C) 8.58
D) Not arithmetic
-
A) 2.86
B) 2.145
C) 8.58
D) Not arithmetic

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
49
If the sequence is arithmetic, find the common difference. If the sequence is not arithmetic, say so.
-
A)
B) 8
C) 2
D) Not arithmetic
-
A)
B) 8
C) 2
D) Not arithmetic

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
50
Write the first five terms of the arithmetic sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
51
Write the first five terms of the arithmetic sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
52
Write the first five terms of the arithmetic sequence.
-
A)
B)
C) , 2
D)
-
A)
B)
C) , 2
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
53
Write the first five terms of the arithmetic sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
54
Write the first five terms of the arithmetic sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
55
Write the first five terms of the arithmetic sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
56
Use the formula for to find the general term for the arithmetic sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
57
Use the formula for to find the general term for the arithmetic sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
58
Use the formula for to find the general term for the arithmetic sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
59
Use the formula for to find the general term for the arithmetic sequence.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
60
Find the indicated term for the arithmetic sequence.
- ;
A) -23
B) 22
C) -26
D) 19
- ;
A) -23
B) 22
C) -26
D) 19

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
61
Find the indicated term for the arithmetic sequence.
- ;
A) 81
B) 83
C) -73
D) -71
- ;
A) 81
B) 83
C) -73
D) -71

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
62
Find the indicated term for the arithmetic sequence.
-
A)
B) -49
C)
D) 35
-
A)
B) -49
C)
D) 35

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
63
Find the indicated term for the arithmetic sequence.
- ; a22
A) 48
B) 50
C) -36
D) -38
- ; a22
A) 48
B) 50
C) -36
D) -38

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
64
Find the indicated term for the arithmetic sequence.
-
A) 4
B) 2
C) 6
D) 8
-
A) 4
B) 2
C) 6
D) 8

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
65
Find the indicated term for the arithmetic sequence.
-
A) -26
B) -5
C) -21
D) 9
-
A) -26
B) -5
C) -21
D) 9

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
66
Find the indicated term for the arithmetic sequence.
-
A) 9
B) 1
C)
D)
-
A) 9
B) 1
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
67
Find the number of terms in the arithmetic sequence.
-
A) 13
B) 14
C) 11
D) 12
-
A) 13
B) 14
C) 11
D) 12

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
68
Find the number of terms in the arithmetic sequence.
-
A) 24
B) 25
C) 23
D) 22
-
A) 24
B) 25
C) 23
D) 22

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
69
Find the number of terms in the arithmetic sequence.
-
A) 12
B) 15
C) 14
D) 13
-
A) 12
B) 15
C) 14
D) 13

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
70
Find the number of terms in the arithmetic sequence.
-
A) 13
B) 16
C) 15
D) 14
-
A) 13
B) 16
C) 15
D) 14

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
71
Find the requested sum for the arithmetic sequence.
-
A) 6
B) -29
C) -24
D) -69
-
A) 6
B) -29
C) -24
D) -69

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
72
Find the requested sum for the arithmetic sequence.
-
A) -66
B) -18
C) -19
D) -60
-
A) -66
B) -18
C) -19
D) -60

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
73
Find the requested sum for the arithmetic sequence.
-
A) -17
B) -35
C) 15
D) -23
-
A) -17
B) -35
C) 15
D) -23

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
74
Find the requested sum for the arithmetic sequence.
-
A) -60
B) 0
C) -90
D) -24
-
A) -60
B) 0
C) -90
D) -24

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
75
Use a formula for to evaluate the series.
-
A) 16
B) 32
C) 34
D) 4
-
A) 16
B) 32
C) 34
D) 4

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
76
Use a formula for to evaluate the series.
-
A)
B) -12
C) -36
D)
-
A)
B) -12
C) -36
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
77
Use a formula for to evaluate the series.
-
A) 7533
B)
C)
D) 7531
-
A) 7533
B)
C)
D) 7531

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
78
An auditorium has 25 rows, with 10 seats in the first row, 12 in the second row, 14 in the third row, and so forth. How many seats are in the auditorium?
A) 850
B) 900
C) 550
D) 500
A) 850
B) 900
C) 550
D) 500

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
79
If a person puts one penny in a piggy bank on the first day, two pennies in on the second day, three pennies in on the third day, and so forth, how much money will be in the bank after 30 days?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck
80
A collection of dimes is arranged in a triangular array, with 14 coins in the base row, 13 in the next, 12 in the next, and so forth. Find the value of the collection.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 190 flashcards in this deck.
Unlock Deck
k this deck


