Deck 9: Prelude to Calculus
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/32
Play
Full screen (f)
Deck 9: Prelude to Calculus
1
Represent the given system of linear equations as a matrix. Use alphabetical order for the variables.
2
Represent the given system of linear equations as a matrix. Use alphabetical order for the variables.
3
Interpret the given matrix as a system of linear equations. Use x for the first variable, y for the second variable, and z for the third variable.
A)
B)
C)
D)
A)
B)
C)
D)
4
Interpret the given matrix as a system of linear equations. Use x for the first variable, y for the second variable, and z for the third variable.
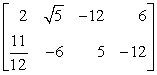
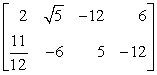

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
5
Interpret the given matrix as a system of linear equations. Use x for the first variable, y for the second variable, and z for the third variable.
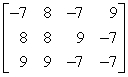
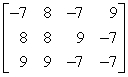

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
6
Use Gaussian elimination to find all solutions to the given system of equations. Work with matrices at least until the back substitution stage is reached. Give the exact answer.
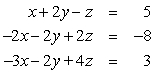
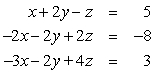

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
7
Use Gaussian elimination to find all solutions to the given system of equations. Work with matrices at least until the back substitution stage is reached.
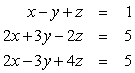
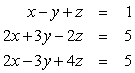

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
8
The solution of the following system of equations is given by x = 1, y = -1, z = 4.
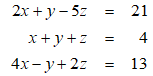
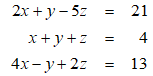

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
9
Find a number b such that the system of linear equations has no solutions. Give the exact answer.
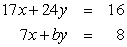
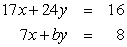

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
10
Find a number b < 49 such that the system of linear equations has infinitely many solutions.
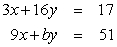
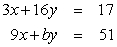

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
11
Find a number b such that the system of linear equations has no solutions. Give the exact answer.
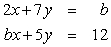
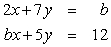

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
12
The system of linear equations has no solutions if and only if b = 5 or b = 0.
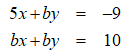
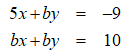

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
13
The system of linear equations has infinitely many solutions.
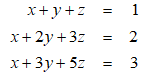
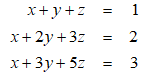

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
14
Find all solutions to the given system of equations.
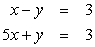
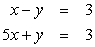

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
15
Find all solutions to the given system of equations. 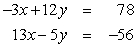
A) (-2, 6)
B) (2, -6)
C) (6, -2)
D) (-6, 2)
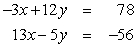
A) (-2, 6)
B) (2, -6)
C) (6, -2)
D) (-6, 2)

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
16
Find all solutions to the given system of equations.
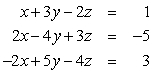
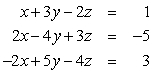

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
17
Determine the value of x in the given system of linear equations.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
18
Use Gaussian elimination to find all solutions to the given system of equations. Work directly with equations rather than matrices.
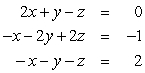
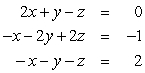

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
19
Use Gaussian elimination to find all solutions to the given system of equations. Work directly with equations rather than matrices.
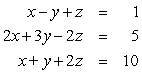
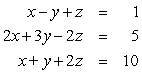

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
20
The solution of the following system of equations is given by x = 1, y = -1, z = 4.
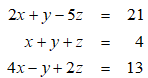
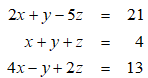

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
21
Find a number b such that the system of linear equations has no solutions. Give the exact answer.
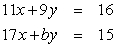
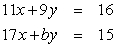

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
22
Find a number b < 61 such that the system of linear equations has infinitely many solutions.
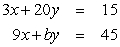
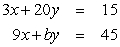

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
23
Find a number b such that the system of linear equations has no solutions. Give the exact answer.
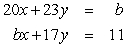
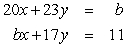

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
24
The system of linear equations has no solutions if and only if b = 12 or b = 0.
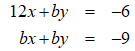
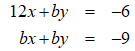

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
25
The system of linear equations has infinitely many solutions.
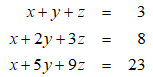
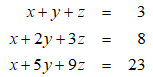

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
26
Use Gaussian elimination to find all solutions to the given system of equations. Work directly with equations rather than matrices.
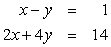
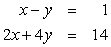

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
27
Use Gaussian elimination to find all solutions to the given system of equations. Work directly with equations rather than matrices. 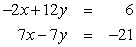
A) (3, 2)
B) (-5, 0)
C) (-3, 0)
D) (0, -3)
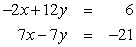
A) (3, 2)
B) (-5, 0)
C) (-3, 0)
D) (0, -3)

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
28
Use Gaussian elimination to find all solutions to the given system of equations. Work directly with equations rather than matrices.
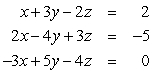
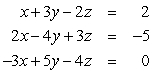

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
29
Find all solutions to the given system of equations.
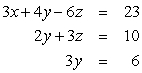
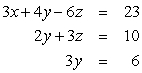

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
30
Find all solutions to the given system of equations.
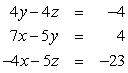
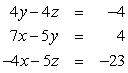

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
31
An ad for a snack consisting of peanuts and raisins states that one serving of the regular snack contains 10 peanuts and 25 raisins and has 110 calories. The lite version of the snack consists of 5 peanuts and 30 raisins per serving and, according to the ad, has 97 calories. How many calories are in each peanut and each raisin?

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck
32
At an educational district's office, three types of employee wages are incorporated into the budget: specialists, managers, and directors. Employees of the same classification earn the same wage district wide. At one location, there are 15 specialists, 5 managers, and 2 directors with a total annual salary budget of $1,070,000. At another location, there are 15 specialists, 2 managers, and 1 director with a total annual salary budget of $771,000. A third location has 14 specialists, 1 manager, and 2 directors with a total annual salary budget of $667,000.

Unlock Deck
Unlock for access to all 32 flashcards in this deck.
Unlock Deck
k this deck


