Deck 10: Sequences and Series
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/124
Play
Full screen (f)
Deck 10: Sequences and Series
1
Evaluate the binomial coefficient 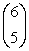
A) 6
B) 720
C) 0.55
D) 30
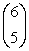
A) 6
B) 720
C) 0.55
D) 30
6
2
Evaluate the binomial coefficient
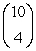
A) 5,040
B) 210
C) 40
D) 52.50
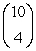
A) 5,040
B) 210
C) 40
D) 52.50
210
3
Evaluate the binomial coefficient
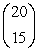
A) 3,876
B) 300
C) 15,504
D) 232,560
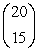
A) 3,876
B) 300
C) 15,504
D) 232,560
15,504
4
Evaluate the binomial coefficient
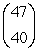
A) 1,367,206.5
B) 2,515,659,960
C) 1,880
D) 62,891,499
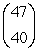
A) 1,367,206.5
B) 2,515,659,960
C) 1,880
D) 62,891,499

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
5
Evaluate the binomial coefficient
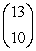
A) 1,037,836,800
B) 286
C) 130
D) 2,860
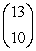
A) 1,037,836,800
B) 286
C) 130
D) 2,860

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
6
Expand (x - 2)5 using the binomial theorem.
A) x5 - 10x4 + 40x3 - 80x2 + 80x - 32
B) x5 + 10x4 + 40x3 + 80x2 + 80x + 32
C) x5 - 10x4 - 40x3 - 80x2 - 80x - 32
D) -x5 + 10x4 - 40x3 + 80x2 - 80x + 32
A) x5 - 10x4 + 40x3 - 80x2 + 80x - 32
B) x5 + 10x4 + 40x3 + 80x2 + 80x + 32
C) x5 - 10x4 - 40x3 - 80x2 - 80x - 32
D) -x5 + 10x4 - 40x3 + 80x2 - 80x + 32

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
7
Expand (4x + 5)3 using the binomial theorem.
A) 125x3 + 100x2 + 80x + 64
B) 64x3 + 80x2 + 100x + 125
C) 125x3 + 300x2 + 240x + 64
D) 64x3 + 240x2 + 300x + 125
A) 125x3 + 100x2 + 80x + 64
B) 64x3 + 80x2 + 100x + 125
C) 125x3 + 300x2 + 240x + 64
D) 64x3 + 240x2 + 300x + 125

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
8
Expand 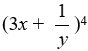 using the binomial theorem.
using the binomial theorem.
A) 81x4 + 108(x3y) + 54(x2y2) + 12(xy3) + 1y4
B) 81x4 + 108(x3/y) + 54(x2/y2) + 12(x/y3) + 1/y4
C) x4 + 12(x3/y) + 54(x2/y2) + 108(x/y3) + 12/y4
D) 81x4 + 27(x3/y) + 9(x2/y2) + 3(x/y3) + 1/y4
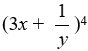 using the binomial theorem.
using the binomial theorem.A) 81x4 + 108(x3y) + 54(x2y2) + 12(xy3) + 1y4
B) 81x4 + 108(x3/y) + 54(x2/y2) + 12(x/y3) + 1/y4
C) x4 + 12(x3/y) + 54(x2/y2) + 108(x/y3) + 12/y4
D) 81x4 + 27(x3/y) + 9(x2/y2) + 3(x/y3) + 1/y4

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
9
Expand (3x - y)4 using Pascal's Triangle.
A) -81x4 + 108x3y - 54x2y2 + 12xy3 - y4
B) 81x4 - 108x3y + 54x2y2 - 12xy3 + y4
C) 81x4 + 108x3y + 54x2y2 + 12xy3 + y4
D) 81x4 - 27x3y + 9x2y2 - 3xy3 + y4
A) -81x4 + 108x3y - 54x2y2 + 12xy3 - y4
B) 81x4 - 108x3y + 54x2y2 - 12xy3 + y4
C) 81x4 + 108x3y + 54x2y2 + 12xy3 + y4
D) 81x4 - 27x3y + 9x2y2 - 3xy3 + y4

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
10
Expand (5x + 3y)3 using Pascal's Triangle.
A) 125x3 + 45x2y + 75xy2 + 27y3
B) 125x3 + 75x2y + 45xy2 + 27y3
C) 125x3 + 225x2y + 135xy2 + 27y3
D) 125x3 + 135x2y + 225xy2 + 27y3
A) 125x3 + 45x2y + 75xy2 + 27y3
B) 125x3 + 75x2y + 45xy2 + 27y3
C) 125x3 + 225x2y + 135xy2 + 27y3
D) 125x3 + 135x2y + 225xy2 + 27y3

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
11
Find the coefficient, C, of the term in the binomial expansion.
Binomial: (x + 5)9 Term: Cx6
A) 125
B) 78,750
C) 900
D) 10,500
Binomial: (x + 5)9 Term: Cx6
A) 125
B) 78,750
C) 900
D) 10,500

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
12
Find the coefficient, C, of the term in the binomial expansion.
Binomial: (x - 4y)6 Term: Cx3y3
A) -1,280
B) 1,280
C) 64
D) -64
Binomial: (x - 4y)6 Term: Cx3y3
A) -1,280
B) 1,280
C) 64
D) -64

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
13
Find the coefficient, C, of the term in the binomial expansion.
Coefficient: (5x + 2y)8 Term: Cx5y3
A) 25,000
B) 3,133
C) 4,000
D) 1,400,000
Coefficient: (5x + 2y)8 Term: Cx5y3
A) 25,000
B) 3,133
C) 4,000
D) 1,400,000

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
14
Find the coefficient, C, of the term in the binomial expansion.
Binomial: (4x - 3y)4 Term: Cxy3
A) 432
B) -432
C) 108
D) -108
Binomial: (4x - 3y)4 Term: Cxy3
A) 432
B) -432
C) 108
D) -108

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
15
Evaluate the binomial coefficient.
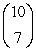
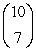

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
16
Expand (2x + 5)4 using the binomial theorem.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
17
In a state lottery in which 5 numbers are drawn from a possible 53 numbers, the number of possible 5 number combinations is equal to:
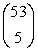 How many possible combinations are there?
How many possible combinations are there?
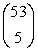 How many possible combinations are there?
How many possible combinations are there?
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
18
Expand the expression using the binomial theorem. 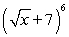
A)
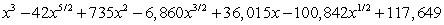
B)
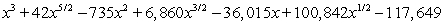
C)
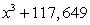
D)
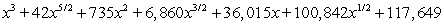
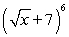
A)
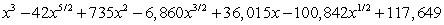
B)
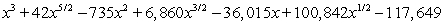
C)
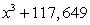
D)
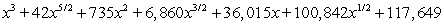

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
19
Expand the expression using the binomial theorem. 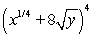
A)
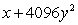
B)
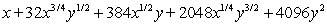
C)
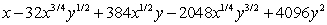
D)
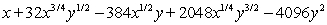
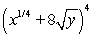
A)
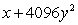
B)
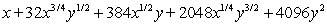
C)
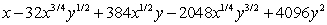
D)
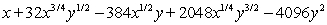

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
20
Evaluate the binomial coefficient
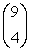
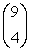

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
21
Evaluate the binomial coefficient
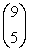
.
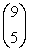
.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
22
Evaluate the binomial coefficient
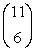
.
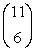
.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
23
Evaluate the binomial coefficient
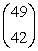
.
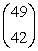
.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
24
Evaluate the binomial coefficient
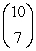
.
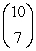
.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
25
Expand (x - 2)5 using the binomial theorem.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
26
Expand (3x + 5)3 using the binomial theorem.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
27
Expand 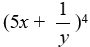 using the binomial theorem.
using the binomial theorem.
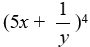 using the binomial theorem.
using the binomial theorem.
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
28
Expand (3x - y)4 using Pascal's Triangle.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
29
Expand (5x + 4y)3 using Pascal's Triangle.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
30
Find the coefficient, C, of the term in the binomial expansion.
Binomial: (x + 3)9 Term: Cx6
Binomial: (x + 3)9 Term: Cx6

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
31
Find the coefficient, C, of the term in the binomial expansion.
Binomial: (x - 3y)6 Term: Cx3y3
Binomial: (x - 3y)6 Term: Cx3y3

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
32
Find the coefficient, C, of the term in the binomial expansion.
Coefficient: (3x + 2y)8 Term: Cx5y3
Coefficient: (3x + 2y)8 Term: Cx5y3

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
33
Find the coefficient, C, of the term in the binomial expansion.
Binomial: (5x - 3y)4 Term: Cxy3
Binomial: (5x - 3y)4 Term: Cxy3

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
34
Prove the statement using mathematical induction for all positive integers, n.
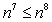
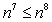

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
35
Prove the statement using mathematical induction for all positive integers, n.
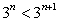
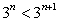

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
36
Prove the statement using mathematical induction for all positive integers, n.
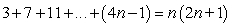
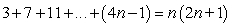

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
37
Prove the statement using mathematical induction for all positive integers, n.
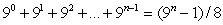
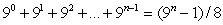

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
38
Prove the statement using mathematical induction for all positive integers, n.
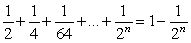
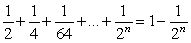

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
39
Prove the statement using mathematical induction for all positive integers, n.
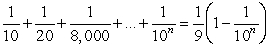
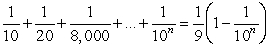

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
40
Prove the statement using mathematical induction for all positive integers, n. For n > 1.
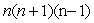 is divisible by 3
is divisible by 3
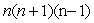 is divisible by 3
is divisible by 3
Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
41
Prove the statement using mathematical induction for all positive integers, n.
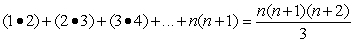
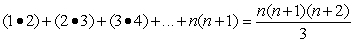

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
42
Prove the statement using mathematical induction for all positive integers, n.
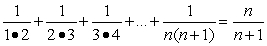
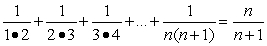

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
43
Prove the statement using mathematical induction for all positive integers, n.
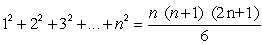
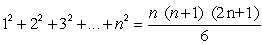

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
44
Which relationship below can be shown to be true through mathematical induction?
A)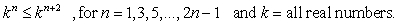
B)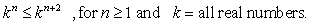
C)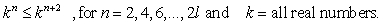
D)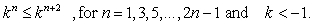
A)
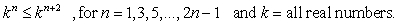
B)
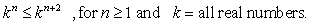
C)
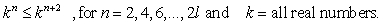
D)
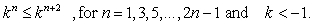

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
45
Apply mathematical induction to prove the formula.
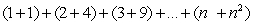
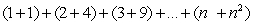

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
46
Prove the statement using mathematical induction for all positive integers, n.
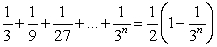
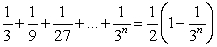

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
47
Determine whether the sequence is geometric. If it is, find the common ratio.
4, 8, 16, 32, 64,...
A) r = -2
B) r = 4
C) r = 2
D) r = -4
4, 8, 16, 32, 64,...
A) r = -2
B) r = 4
C) r = 2
D) r = -4

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
48
Determine whether the sequence is geometric. If it is, find the common ratio.
-4, 8, -16, 32, -64,...
A) r = -12
B) r = -2
C) r = 12
D) r = 2
-4, 8, -16, 32, -64,...
A) r = -12
B) r = -2
C) r = 12
D) r = 2

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
49
Determine whether the sequence is geometric. If it is, find the common ratio. 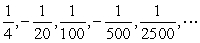
A)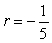
B)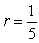
C)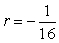
D)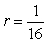
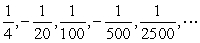
A)
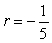
B)
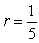
C)
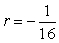
D)
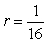

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
50
Write the first four terms of the geometric sequence with a1 = -6 and r = -3.
A) a1 = -6, a2 = 9, a3 = -12, a4 = 15
B) a1 = -6, a2 = -9, a3 = -12, a4 = -15
C) a1 = 6, a2 = -18, a3 = 54, a4 = -162
D) a1 = -6, a2 = 18, a3 = -54, a4 = 162
A) a1 = -6, a2 = 9, a3 = -12, a4 = 15
B) a1 = -6, a2 = -9, a3 = -12, a4 = -15
C) a1 = 6, a2 = -18, a3 = 54, a4 = -162
D) a1 = -6, a2 = 18, a3 = -54, a4 = 162

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
51
Write the first four terms of the geometric sequence with a1 = 64 and r =
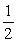
A) a1 = -64, a2 = -128, a3 = -256, a4 = -512
B) a1 = 64, a2 = 128, a3 = 256, a4 = 512
C) a1 = -64, a2 = -32, a3 = -16, a4 = -8
D) a1 = 64, a2 = 32, a3 = 16, a4 = 8
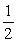
A) a1 = -64, a2 = -128, a3 = -256, a4 = -512
B) a1 = 64, a2 = 128, a3 = 256, a4 = 512
C) a1 = -64, a2 = -32, a3 = -16, a4 = -8
D) a1 = 64, a2 = 32, a3 = 16, a4 = 8

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
52
Write the formula for the nth term of the geometric sequence with a1 = 6 and r = -6.
A) an = -6(6)n-1
B) an = -6(6)n+1
C) an = 6(-6)n-1
D) an = 6(-6)n+1
A) an = -6(6)n-1
B) an = -6(6)n+1
C) an = 6(-6)n-1
D) an = 6(-6)n+1

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
53
Write the formula for the nth term of the geometric sequence with a1 = 4 and r =
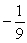
A)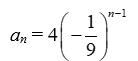
B)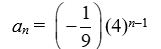
C) an = 4(9)n-1
D)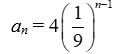
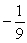
A)
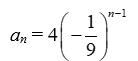
B)
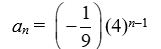
C) an = 4(9)n-1
D)
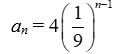

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
54
Find the 9th term of the geometric sequence 5, 20, 80, 320,...
A) 327,680
B) 1,310,720
C) 1,953,125
D) 1,562,500
A) 327,680
B) 1,310,720
C) 1,953,125
D) 1,562,500

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
55
Find the 6th term of the geometric sequence 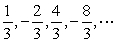
A)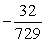
B)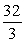
C)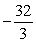
D)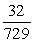
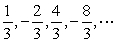
A)
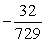
B)
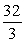
C)
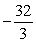
D)
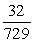

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
56
Find the sum of the finite geometric series 1 + 4 + 16 + 64 + ... + 4096.
A) 4,181
B) 5,461
C) 729
D) 3,277
A) 4,181
B) 5,461
C) 729
D) 3,277

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
57
Find the sum of the finite geometric series
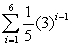
A) 364
B) 36.5
C) -6.4
D) 72.8
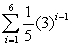
A) 364
B) 36.5
C) -6.4
D) 72.8


Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
58
Find the sum of the infinite geometric series 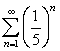
A)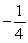
B)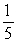
C)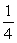
D)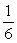
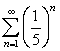
A)
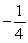
B)
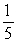
C)
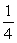
D)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
59
Find the sum of the infinite geometric series
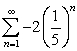
A)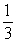
B)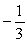
C)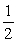
D)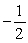
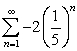
A)
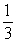
B)
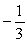
C)
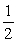
D)
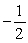

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
60
At the time she was hired, Nema's salary was $35,000 per year. If she is given an annual salary increase of 4% per year, what will her salary be after 12 years?
A) $56,036.13
B) $400,400.00
C) $53,880.89
D) $436,800.00
A) $56,036.13
B) $400,400.00
C) $53,880.89
D) $436,800.00

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
61
Adrienne bought a condominium in 2005 for $155,000. She expects it to appreciate 4% per year. Calculate the expected value of the condominium after 14 years.
A) $258,086.39
B) $268,409.85
C) $86,800.00
D) $80,600.00
A) $258,086.39
B) $268,409.85
C) $86,800.00
D) $80,600.00

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
62
Write the formula for the nth term of the geometric sequence with a1 = 8 and r = -3.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
63
The population of a city increased at the rate of 3% every year over an eight-year period. If the population was 1,000 in 2001, what was the population in 2006?

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
64
A bungee jumper rebounds 68% of the height jumped. Assuming the bungee jump is made with a cord that stretches to 340 feet, how far will the bungee jumper travel upward on the fourth rebound?
A) On the fourth rebound, the jumper will reach a height approximately 49 feet.
B) On the fourth rebound, the jumper will reach a height approximately 107 feet.
C) On the fourth rebound, the jumper will reach a height approximately 73 feet.
D) On the fourth rebound, the jumper will reach a height approximately 925 feet.
A) On the fourth rebound, the jumper will reach a height approximately 49 feet.
B) On the fourth rebound, the jumper will reach a height approximately 107 feet.
C) On the fourth rebound, the jumper will reach a height approximately 73 feet.
D) On the fourth rebound, the jumper will reach a height approximately 925 feet.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
65
Find the sum of the finite geometric series 4 + 8 + 16 + 32 + ... + 256.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
66
Find the sum of the finite geometric series
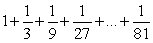
. Round the answer to 3 decimal places if necessary.
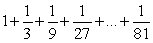
. Round the answer to 3 decimal places if necessary.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
67
Find the sum of the infinite geometric series
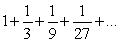
. Round the answer to 3 decimal places if necessary.
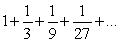
. Round the answer to 3 decimal places if necessary.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
68
Find the sum of the finite geometric series
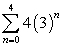
.
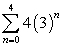
.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
69
Find the sum of the finite geometric series
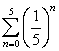
. Round the answer to 3 decimal places if necessary.
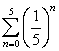
. Round the answer to 3 decimal places if necessary.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
70
Find the sum of the infinite geometric series
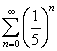
. Round the answer to 3 decimal places if necessary.
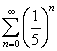
. Round the answer to 3 decimal places if necessary.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
71
Determine whether the sequence is arithmetic. If it is, find the common difference d.
6, 7, 8, 9, 10,...
A) d = -1
B) d = 1
C) d = 4
D) d = 7
6, 7, 8, 9, 10,...
A) d = -1
B) d = 1
C) d = 4
D) d = 7

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
72
Determine whether the sequence is arithmetic. If it is, find the common difference d.
59, 55, 51, 47, 43,...
A) d = -16
B) d = 16
C) d = 4
D) d = -4
59, 55, 51, 47, 43,...
A) d = -16
B) d = 16
C) d = 4
D) d = -4

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
73
Find the first four terms of the sequence an = -5n + 5. Determine whether the sequence is arithmetic, and if so, find the common difference d.
A) a1 = 10, a2 = 15, a3 = 20, a4 = 25; not arithmetic
B) a1 = 0, a2 = -5, a3 = -10, a4 = -15; not arithmetic
C) a1 = 10, a2 = 15, a3 = 20, a4 = 25; d = 5
D) a1 = 0, a2 = -5, a3 = -10, a4 = -15; d = -5
A) a1 = 10, a2 = 15, a3 = 20, a4 = 25; not arithmetic
B) a1 = 0, a2 = -5, a3 = -10, a4 = -15; not arithmetic
C) a1 = 10, a2 = 15, a3 = 20, a4 = 25; d = 5
D) a1 = 0, a2 = -5, a3 = -10, a4 = -15; d = -5

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
74
Find the first four terms of the sequence an = 7(n - 3). Determine whether the sequence is arithmetic, and if so, find the common difference d.
A) a1 = -14, a2 = -7, a3 = 0, a4 = 7; not arithmetic
B) a1 = -14, a2 = -7, a3 = 0, a4 = 7; d = 7
C) a1 = 14, a2 = 7, a3 = 0, a4 = -7; not arithmetic
D) a1 = -14, a2 = -7, a3 = 0, a4 = 7; d = -7
A) a1 = -14, a2 = -7, a3 = 0, a4 = 7; not arithmetic
B) a1 = -14, a2 = -7, a3 = 0, a4 = 7; d = 7
C) a1 = 14, a2 = 7, a3 = 0, a4 = -7; not arithmetic
D) a1 = -14, a2 = -7, a3 = 0, a4 = 7; d = -7

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
75
Find the first four terms of the sequence an = (-1)n+2(7n). Determine whether the sequence is arithmetic, and if so, find the common difference d.
A) a1 = -7, a2 = 14, a3 = -21, a4 = 28; not arithmetic
B) a1 = -7, a2 = 14, a3 = -21, a4 = 28; d = 7
C) a1 = -7, a2 = 14, a3 = -21, a4 = 28; d = -7
D) a1 = 7, a2 = -14, a3 = 21, a4 = -28; not arithmetic
A) a1 = -7, a2 = 14, a3 = -21, a4 = 28; not arithmetic
B) a1 = -7, a2 = 14, a3 = -21, a4 = 28; d = 7
C) a1 = -7, a2 = 14, a3 = -21, a4 = 28; d = -7
D) a1 = 7, a2 = -14, a3 = 21, a4 = -28; not arithmetic

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
76
Find the general, or nth, term of the arithmetic sequence given the first term a1 = -7 and the common difference d = -2.
A) an = -5n - 2
B) an = 5n - 2
C) an = -2n - 5
D) an = -7n + -2
A) an = -5n - 2
B) an = 5n - 2
C) an = -2n - 5
D) an = -7n + -2

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
77
Find the general, or nth, term of the arithmetic sequence given the first term a1 = 2 and the common difference d = k.
A) an = kn + (2 + k)
B) an = kn + (2 - k)
C) an = 2n + (2 - k)
D) an = kn - (2 - k)
A) an = kn + (2 + k)
B) an = kn + (2 - k)
C) an = 2n + (2 - k)
D) an = kn - (2 - k)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
78
Find the general, or nth, term of the arithmetic sequence given the first term a1 = -10 and the common difference d =
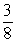
A)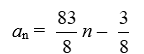
B)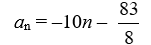
C)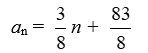
D)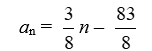
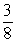
A)
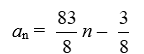
B)
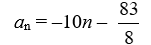
C)
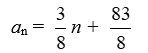
D)
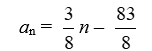

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
79
Find the 10th term of the arithmetic sequence 9, 13, 17, 21, 25,...
A) 85
B) 53
C) 49
D) 45
A) 85
B) 53
C) 49
D) 45

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
80
Find the 195th term of the arithmetic sequence -5, 1, 7, 13,...
A) 1,159
B) 1,165
C) 1,171
D) -1,000
A) 1,159
B) 1,165
C) 1,171
D) -1,000

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck


