Deck 9: Conics, Systems of Nonlinear Equations and Inequalities, and Parametric Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/230
Play
Full screen (f)
Deck 9: Conics, Systems of Nonlinear Equations and Inequalities, and Parametric Equations
1
Graph the curve defined by the parametric equations.
x= t , y= t2 , t in [-2, 2]
x= t , y= t2 , t in [-2, 2]
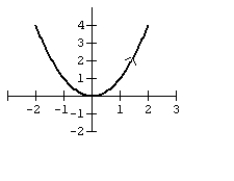
2
Graph the curve defined by the parametric equations.
![Graph the curve defined by the parametric equations. , ,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a14_a8a5_d53b9504a056_TB10663_00.jpg) ,
, ![Graph the curve defined by the parametric equations. , ,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a15_a8a5_1b57be2bb7b9_TB10663_00.jpg) ,t in [0, 2π]
,t in [0, 2π]
![Graph the curve defined by the parametric equations. , ,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a14_a8a5_d53b9504a056_TB10663_00.jpg) ,
, ![Graph the curve defined by the parametric equations. , ,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a15_a8a5_1b57be2bb7b9_TB10663_00.jpg) ,t in [0, 2π]
,t in [0, 2π]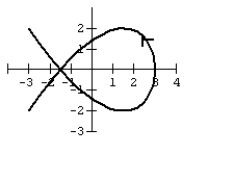
3
Graph the curve defined by the parametric equations.
![Graph the curve defined by the parametric equations. ,y=t,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a17_a8a5_ad47cfa028f0_TB10663_00.jpg) ,y=t,t in [0, 2π]
,y=t,t in [0, 2π]
![Graph the curve defined by the parametric equations. ,y=t,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a17_a8a5_ad47cfa028f0_TB10663_00.jpg) ,y=t,t in [0, 2π]
,y=t,t in [0, 2π]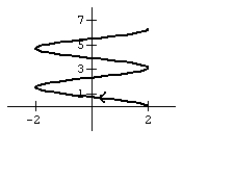
4
Graph the curve defined by the parametric equations.
![Graph the curve defined by the parametric equations. , ,t in [0, 1]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a19_a8a5_bdf37051c310_TB10663_00.jpg) ,
, ![Graph the curve defined by the parametric equations. , ,t in [0, 1]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a1a_a8a5_f1c961783a67_TB10663_00.jpg) ,t in [0, 1]
,t in [0, 1]
![Graph the curve defined by the parametric equations. , ,t in [0, 1]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a19_a8a5_bdf37051c310_TB10663_00.jpg) ,
, ![Graph the curve defined by the parametric equations. , ,t in [0, 1]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a1a_a8a5_f1c961783a67_TB10663_00.jpg) ,t in [0, 1]
,t in [0, 1]
Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
5
Graph the curve defined by the parametric equations.
![Graph the curve defined by the parametric equations. , ,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a1c_a8a5_a7145e9d4d96_TB10663_00.jpg) ,
, ![Graph the curve defined by the parametric equations. , ,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a1d_a8a5_c5fff45959d3_TB10663_00.jpg) ,t in [0, 2π]
,t in [0, 2π]
![Graph the curve defined by the parametric equations. , ,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a1c_a8a5_a7145e9d4d96_TB10663_00.jpg) ,
, ![Graph the curve defined by the parametric equations. , ,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a1d_a8a5_c5fff45959d3_TB10663_00.jpg) ,t in [0, 2π]
,t in [0, 2π]
Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
6
Graph the curve defined by the parametric equations.
![Graph the curve defined by the parametric equations. , ,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a1f_a8a5_b19069536c98_TB10663_00.jpg) ,
, ![Graph the curve defined by the parametric equations. , ,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a20_a8a5_f7d09269dc66_TB10663_00.jpg) ,t in [0, 2π]
,t in [0, 2π]
![Graph the curve defined by the parametric equations. , ,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a1f_a8a5_b19069536c98_TB10663_00.jpg) ,
, ![Graph the curve defined by the parametric equations. , ,t in [0, 2π]](https://storage.examlex.com/TB10663/11eed1b2_575d_9a20_a8a5_f7d09269dc66_TB10663_00.jpg) ,t in [0, 2π]
,t in [0, 2π]
Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
7
Graph the curve defined by the parametric equations.
![Graph the curve defined by the parametric equations. , ,t in [-π/4,π/4]](https://storage.examlex.com/TB10663/11eed1b2_575d_c132_a8a5_23b1280af6ba_TB10663_00.jpg) ,
, ![Graph the curve defined by the parametric equations. , ,t in [-π/4,π/4]](https://storage.examlex.com/TB10663/11eed1b2_575d_c133_a8a5_211dfd65d254_TB10663_00.jpg) ,t in [-π/4,π/4]
,t in [-π/4,π/4]
![Graph the curve defined by the parametric equations. , ,t in [-π/4,π/4]](https://storage.examlex.com/TB10663/11eed1b2_575d_c132_a8a5_23b1280af6ba_TB10663_00.jpg) ,
, ![Graph the curve defined by the parametric equations. , ,t in [-π/4,π/4]](https://storage.examlex.com/TB10663/11eed1b2_575d_c133_a8a5_211dfd65d254_TB10663_00.jpg) ,t in [-π/4,π/4]
,t in [-π/4,π/4]
Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
8
The given parametric equations define a plane curve. Find an equation in rectangular form that also corresponds to the plane curve.
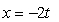 ,
, 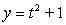
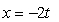 ,
, 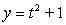

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
9
The given parametric equations define a plane curve. Find an equation in rectangular form that also corresponds to the plane curve.
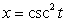 ,
, 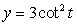
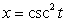 ,
, 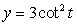

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
10
The given parametric equations define a plane curve. Find an equation in rectangular form that also corresponds to the plane curve.
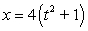 ,
, 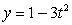
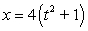 ,
, 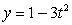

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
11
The given parametric equations define a plane curve. Find an equation in rectangular form that also corresponds to the plane curve.
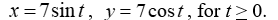
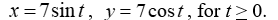

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
12
The given parametric equations define a plane curve. Find an equation in rectangular form that also corresponds to the plane curve.
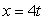 ,
, 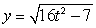
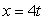 ,
, 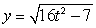

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
13
Recall that the flight of a projectile can be modeled with the parametric equations:
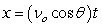 ,
, 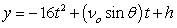 where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
A projectile is launched at a speed of 560 ft/sec at an angle of 47° with the horizontal. After how many seconds does the projectile hit the ground? Round to one decimal place.
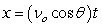 ,
, 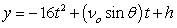 where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.A projectile is launched at a speed of 560 ft/sec at an angle of 47° with the horizontal. After how many seconds does the projectile hit the ground? Round to one decimal place.

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
14
Recall that the flight of a projectile can be modeled with the parametric equations:
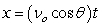 ,
, 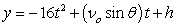
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
A projectile is launched at a speed of 465 ft/sec at an angle of 33° with the horizontal. How far does the projectile travel (what is the horizontal distance), and what is the maximum altitude? Round to the nearest integer.
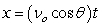 ,
, 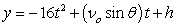
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
A projectile is launched at a speed of 465 ft/sec at an angle of 33° with the horizontal. How far does the projectile travel (what is the horizontal distance), and what is the maximum altitude? Round to the nearest integer.

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
15
Recall that the flight of a projectile can be modeled with the parametric equations:
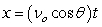 ,
, 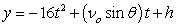
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
A baseball is hit at an initial speed of 115 mph and angle of 32° at a height of 2 feet above the ground. If home plate is 425 feet from the back fence, which is 12 feet tall, will the baseball clear the back fence for a home run?
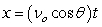 ,
, 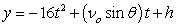
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
A baseball is hit at an initial speed of 115 mph and angle of 32° at a height of 2 feet above the ground. If home plate is 425 feet from the back fence, which is 12 feet tall, will the baseball clear the back fence for a home run?

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
16
Recall that the flight of a projectile can be modeled with the parametric equations:
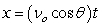 ,
, 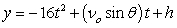 where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
A baseball is hit at an initial speed of 110 mph and angle of 31° at a height of 2 feet above the ground. If there's no back fence or other obstruction, how far does the baseball travel (horizontal distance), and what is the maximum height? Round to one decimal place.
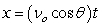 ,
, 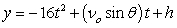 where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.A baseball is hit at an initial speed of 110 mph and angle of 31° at a height of 2 feet above the ground. If there's no back fence or other obstruction, how far does the baseball travel (horizontal distance), and what is the maximum height? Round to one decimal place.

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
17
Recall that the flight of a projectile can be modeled with the parametric equations:
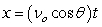 ,
, 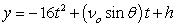 where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
A gun is fired at an angle of 21°, and the bullet has an initial speed of 875 feet per second. How high does the bullet go, and when does it hit the ground? Round the altitude to the nearest foot and time to the nearest tenth of a second.
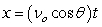 ,
, 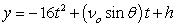 where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.A gun is fired at an angle of 21°, and the bullet has an initial speed of 875 feet per second. How high does the bullet go, and when does it hit the ground? Round the altitude to the nearest foot and time to the nearest tenth of a second.

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
18
Recall that the flight of a projectile can be modeled with the parametric equations:
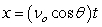 ,
, 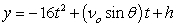 where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
A missile is fired from a ship at an angle of 32°, an initial height of 20 feet above the water's surface, and at a speed of 4450 feet per second. How long will it be before the missile hits the water? Round to the nearest tenth of a second.
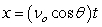 ,
, 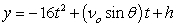 where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.A missile is fired from a ship at an angle of 32°, an initial height of 20 feet above the water's surface, and at a speed of 4450 feet per second. How long will it be before the missile hits the water? Round to the nearest tenth of a second.

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
19
Recall that the flight of a projectile can be modeled with the parametric equations:
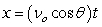 ,
, 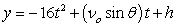 where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
A missile is fired from a ship at an angle of 56°, an initial height of 18 feet above the water's surface, and at a speed of 4430 feet per second. Will it be able to hit a target that is 2.4 miles away?
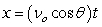 ,
, 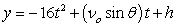 where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.A missile is fired from a ship at an angle of 56°, an initial height of 18 feet above the water's surface, and at a speed of 4430 feet per second. Will it be able to hit a target that is 2.4 miles away?

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
20
Recall that the flight of a projectile can be modeled with the parametric equations:
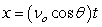 ,
, 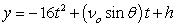 where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
A projectile is launched at a speed of 200 ft/sec at an angle of 30° with the horizontal. Plot the path of the projectile on a graph.
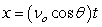 ,
, 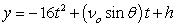 where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.
where t is in seconds, νo is the initial velocity, θ is the angle with the horizontal, and x and y are in feet.A projectile is launched at a speed of 200 ft/sec at an angle of 30° with the horizontal. Plot the path of the projectile on a graph.

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
21
Graph the curve defined by the parametric equations.
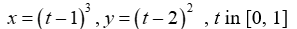
A)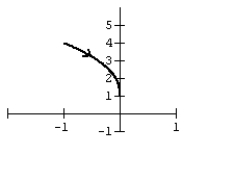
B)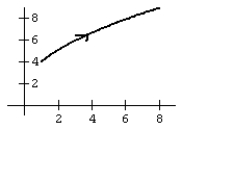
C)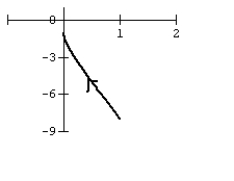
D)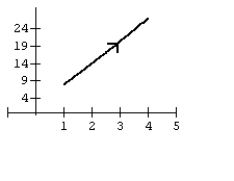
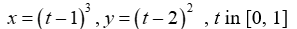
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
22
Graph the curve defined by the parametric equations.
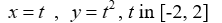
A)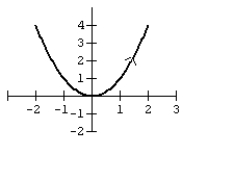
B)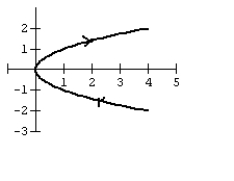
C)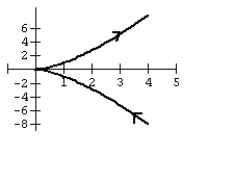
D)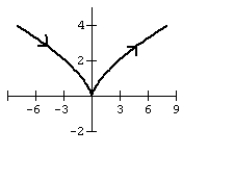
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
23
Graph the curve defined by the parametric equations.
A)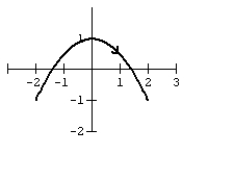
B)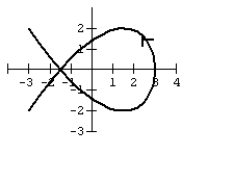
C)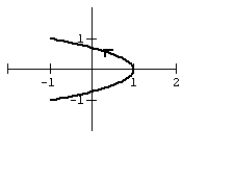
D)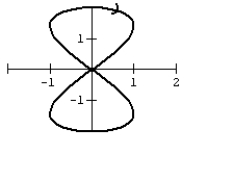
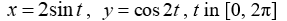
A)

B)
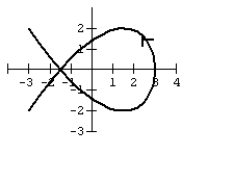
C)

D)


Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
24
Graph the curve defined by the parametric equations.
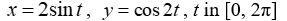
A)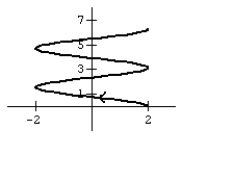
B)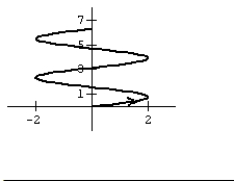
C)
D)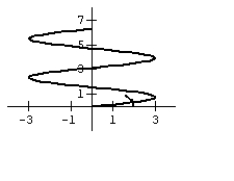
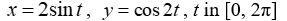
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
25
Graph the curve defined by the parametric equations.
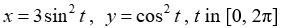
A)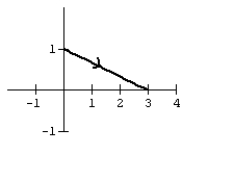
B)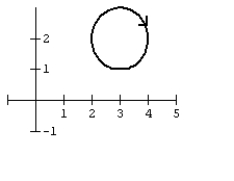
C)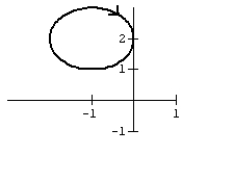
D)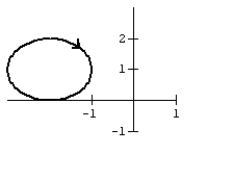
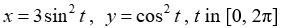
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
26
Graph the curve defined by the parametric equations.
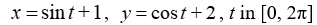
A)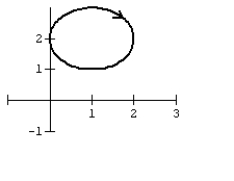
B)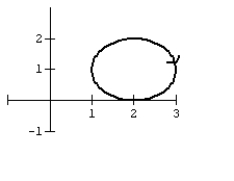
C)
D)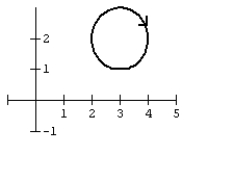
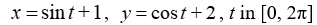
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
27
Graph the curve defined by the parametric equations.
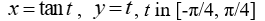
A)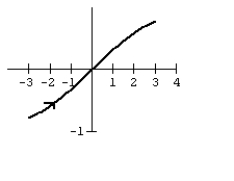
B)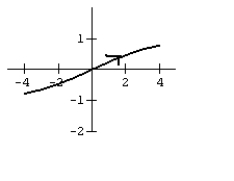
C)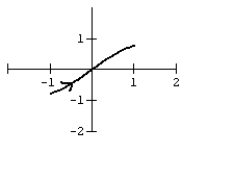
D)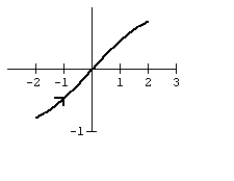
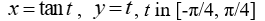
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
28
The given parametric equations define a plane curve. Find an equation in rectangular form that also corresponds to the plane curve.
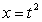 ,
, 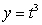
A)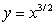
B)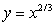
C)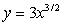
D)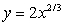
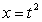 ,
, 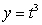
A)
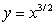
B)
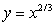
C)
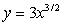
D)
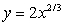

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
29
The given parametric equations define a plane curve. Find an equation in rectangular form that also corresponds to the plane curve.
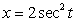 ,
, 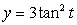
A)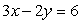
B)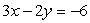
C)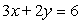
D)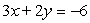
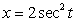 ,
, 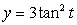
A)
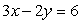
B)
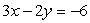
C)
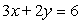
D)
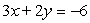

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
30
The given parametric equations define a plane curve. Find an equation in rectangular form that also corresponds to the plane curve.
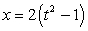 ,
, 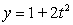
A)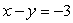
B)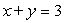
C)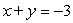
D)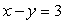
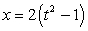 ,
, 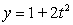
A)
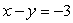
B)
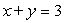
C)
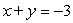
D)
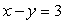

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
31
The given parametric equations define a plane curve. Find an equation in rectangular form that also corresponds to the plane curve.
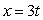 ,
, 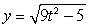
A)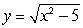
B)
C)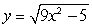
D)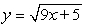
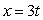 ,
, 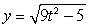
A)
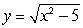
B)
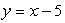
C)
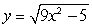
D)
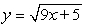

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
32
Recall that the flight of a projectile can be modeled with the parametric equations:
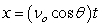 ,
, 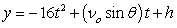 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
A projectile is launched at a speed of 420 ft/sec at an angle of 37° with the horizontal. After how many seconds does the projectile hit the ground? Round to one decimal place.
A) 15.8 seconds
B) 31.6 seconds
C) 7.9 seconds
D) 21.0 seconds
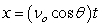 ,
, 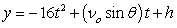 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.A projectile is launched at a speed of 420 ft/sec at an angle of 37° with the horizontal. After how many seconds does the projectile hit the ground? Round to one decimal place.
A) 15.8 seconds
B) 31.6 seconds
C) 7.9 seconds
D) 21.0 seconds

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
33
Recall that the flight of a projectile can be modeled with the parametric equations:
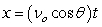 ,
, 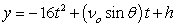 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
A projectile is launched at a speed of 520 ft/sec at an angle of 31° with the horizontal. How far does the projectile travel (what is the horizontal distance), and what is the maximum altitude? Round to the nearest integer.
A) 7,461 feet; 1,121 feet
B) 14,922 feet; 1,121 feet
C) 7,461 feet; 2,241 feet
D) 14,922 feet; 2,241 feet
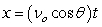 ,
, 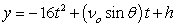 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.A projectile is launched at a speed of 520 ft/sec at an angle of 31° with the horizontal. How far does the projectile travel (what is the horizontal distance), and what is the maximum altitude? Round to the nearest integer.
A) 7,461 feet; 1,121 feet
B) 14,922 feet; 1,121 feet
C) 7,461 feet; 2,241 feet
D) 14,922 feet; 2,241 feet

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
34
Recall that the flight of a projectile can be modeled with the parametric equations:
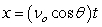 ,
, 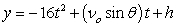 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
A baseball is hit at an initial speed of 100 mph and angle of 32° at a height of 3 feet above the ground. If home plate is 465 feet from the back fence, which is 19 feet tall, will the baseball clear the back fence for a home run?
A) Yes. The height will be over 19 feet at that time.
B) No. The height will not be over 19 feet at that time.
C) no solution
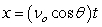 ,
, 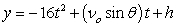 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.A baseball is hit at an initial speed of 100 mph and angle of 32° at a height of 3 feet above the ground. If home plate is 465 feet from the back fence, which is 19 feet tall, will the baseball clear the back fence for a home run?
A) Yes. The height will be over 19 feet at that time.
B) No. The height will not be over 19 feet at that time.
C) no solution

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
35
Recall that the flight of a projectile can be modeled with the parametric equations:
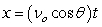 ,
, 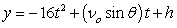 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
A baseball is hit at an initial speed of 110 mph and angle of 24° at a height of 5 feet above the ground. If there's no back fence or other obstruction, how far does the baseball travel (horizontal distance), and what is the maximum height? Round to one decimal place.
A) 615.5 feet; 72.3 feet
B) 604.5 feet; 72.3 feet
C) 615.5 feet; 67.3 feet
D) 604.5 feet; 165.4 feet
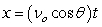 ,
, 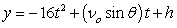 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.A baseball is hit at an initial speed of 110 mph and angle of 24° at a height of 5 feet above the ground. If there's no back fence or other obstruction, how far does the baseball travel (horizontal distance), and what is the maximum height? Round to one decimal place.
A) 615.5 feet; 72.3 feet
B) 604.5 feet; 72.3 feet
C) 615.5 feet; 67.3 feet
D) 604.5 feet; 165.4 feet

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
36
Recall that the flight of a projectile can be modeled with the parametric equations:
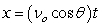 ,
, 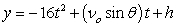 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
A gun is fired at an angle of 23°, and the bullet has an initial speed of 2345 feet per second. How high does the bullet go, and when does it hit the ground? Round the altitude to the nearest foot and time to the nearest tenth of a second.
A) 13,118 feet; 57.3 seconds
B) 26,236 feet; 57.3 seconds
C) 13,118 feet; 29 seconds
D) 33,573 feet; 29 seconds
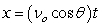 ,
, 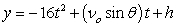 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.A gun is fired at an angle of 23°, and the bullet has an initial speed of 2345 feet per second. How high does the bullet go, and when does it hit the ground? Round the altitude to the nearest foot and time to the nearest tenth of a second.
A) 13,118 feet; 57.3 seconds
B) 26,236 feet; 57.3 seconds
C) 13,118 feet; 29 seconds
D) 33,573 feet; 29 seconds

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
37
Recall that the flight of a projectile can be modeled with the parametric equations:
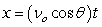 ,
, 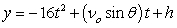 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
A missile is fired from a ship at an angle of 31°, an initial height of 13 feet above the water's surface, and at a speed of 5500 feet per second. How long will it be before the missile hits the water? Round to one decimal place.
A) 177.0 seconds
B) 354.1 seconds
C) 88.5 seconds
D) 294.7 seconds
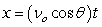 ,
, 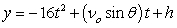 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.A missile is fired from a ship at an angle of 31°, an initial height of 13 feet above the water's surface, and at a speed of 5500 feet per second. How long will it be before the missile hits the water? Round to one decimal place.
A) 177.0 seconds
B) 354.1 seconds
C) 88.5 seconds
D) 294.7 seconds

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
38
Recall that the flight of a projectile can be modeled with the parametric equations:
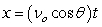 ,
, 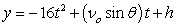 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
A missile is fired from a ship at an angle of 39°, an initial height of 20 feet above the water's surface, and at a speed of 3890 feet per second. Will it be able to hit a target that is 2.4 miles away?
A) Yes, it will easily hit the target.
B) No, it will miss the target.
C) no solution
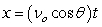 ,
, 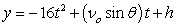 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.A missile is fired from a ship at an angle of 39°, an initial height of 20 feet above the water's surface, and at a speed of 3890 feet per second. Will it be able to hit a target that is 2.4 miles away?
A) Yes, it will easily hit the target.
B) No, it will miss the target.
C) no solution

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
39
Recall that the flight of a projectile can be modeled with the parametric equations:
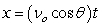 ,
, 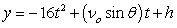 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
A projectile is launched at a speed of 200 ft/sec at an angle of 60° with the horizontal. Plot the path of the projectile on a graph.
A)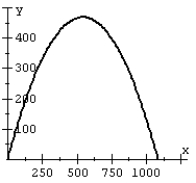
B)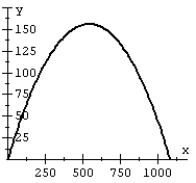
C)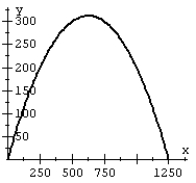
D)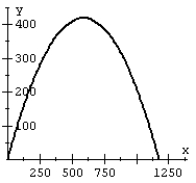
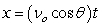 ,
, 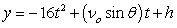 where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.
where t is in seconds, vo is the initial velocity, is the angle with the horizontal, and x and y are in feet.A projectile is launched at a speed of 200 ft/sec at an angle of 60° with the horizontal. Plot the path of the projectile on a graph.
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
40
The given rectangular equation defines a plane curve. Find the parametric equations that also corresponds to the plane curve.
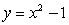
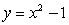

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
41
The given rectangular equation defines a plane curve. Find the parametric equations that also corresponds to the plane curve.
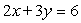
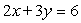

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
42
The given rectangular equation defines a plane curve. Find the parametric equations that also corresponds to the plane curve.
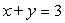
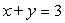

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
43
The given rectangular equation defines a plane curve. Find the parametric equations that also corresponds to the plane curve.
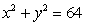
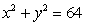

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
44
The given rectangular equation defines a plane curve. Find the parametric equations that also corresponds to the plane curve.
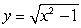
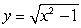

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
45
Find the polar equation that represents the conic described (assume the focus is at the origin).
Ellipse with eccentricity e =
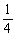
and directrix
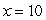
Ellipse with eccentricity e =
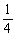
and directrix
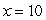

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
46
Find the polar equation that represents the conic described (assume the focus is at the origin).
Hyperbola with eccentricity e =
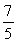
and directrix
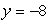
Hyperbola with eccentricity e =
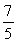
and directrix
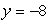

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
47
Find the polar equation that represents the conic described (assume the focus is at the origin).
Parabola with eccentricity e =1 and directrix
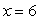
Parabola with eccentricity e =1 and directrix
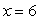

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
48
Identify the conic that the polar equation represents.
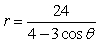
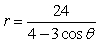

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
49
Identify the conic that the polar equation represents.
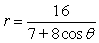
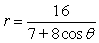

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
50
Identify the conic that the polar equation represents.
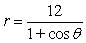
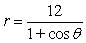

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
51
For the polar equation, (a) Identify the conic as either a parabola, ellipse, or hyperbola; (b) find the eccentricity and vertex (or vertices); and (c) graph.
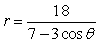
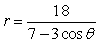

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
52
For the polar equation, (a) Identify the conic as either a parabola, ellipse, or hyperbola; (b) find the eccentricity and vertex (or vertices); and (c) graph.
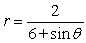
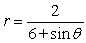

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
53
For the polar equation, graph the conic. 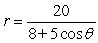
A)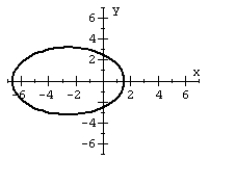
B)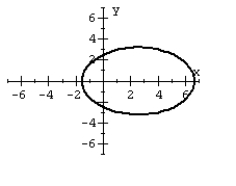
C)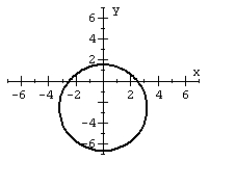
D)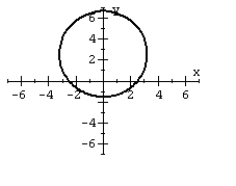
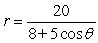
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
54
For the polar equation, graph the conic. 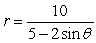
A)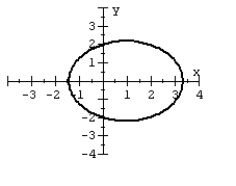
B)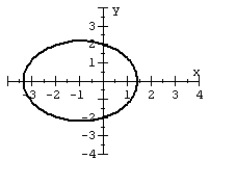
C)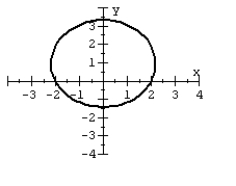
D)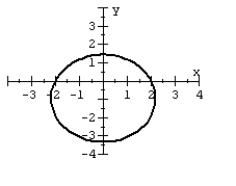
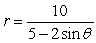
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
55
For the polar equation, (a) Identify the conic as either a parabola, ellipse, or hyperbola; (b) find the eccentricity and vertex (or vertices); and (c) graph.
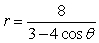
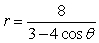

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
56
For the polar equation, (a) Identify the conic as either a parabola, ellipse, or hyperbola; (b) find the eccentricity and vertex (or vertices); and (c) graph.
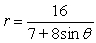
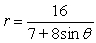

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
57
For the polar equation, graph the conic. 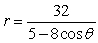
A)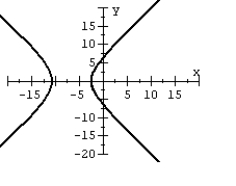
B)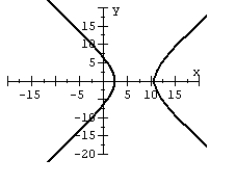
C)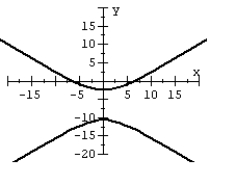
D)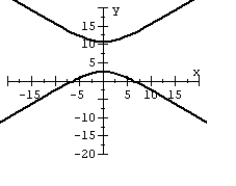
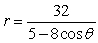
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
58
For the polar equation, graph the conic. 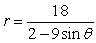
A)
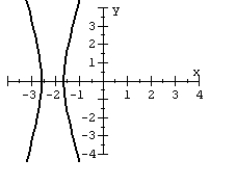
B)
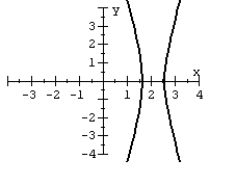
C)
D)
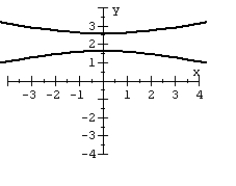
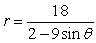
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
59
For the polar equation, (a) Identify the conic as either a parabola, ellipse, or hyperbola; (b) find the eccentricity and vertex (or vertices); and (c) graph.
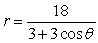
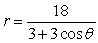

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
60
For the polar equation, (a) Identify the conic as either a parabola, ellipse, or hyperbola; (b) find the eccentricity and vertex (or vertices); and (c) graph.
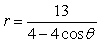
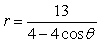

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
61
For the polar equation, (a) Identify the conic as either a parabola, ellipse, or hyperbola; (b) find the eccentricity and vertex (or vertices); and (c) graph.
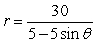
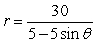

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
62
For the polar equation, graph the conic. 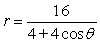
A)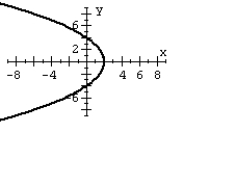
B)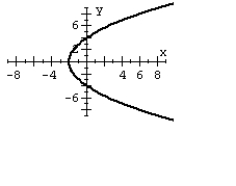
C)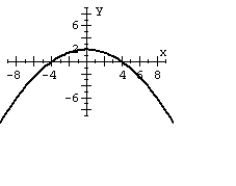
D)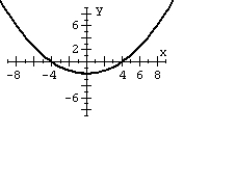
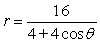
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
63
For the polar equation, graph the conic. 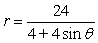
A)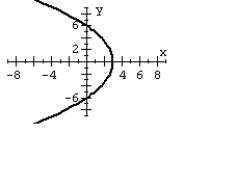
B)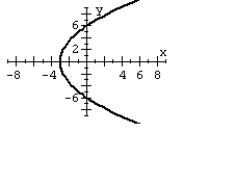
C)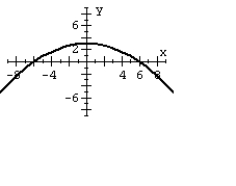
D)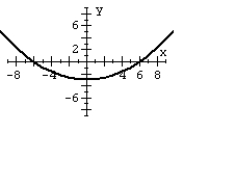
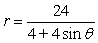
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
64
Identify the conic (parabola, ellipse, or hyperbola) that is represented by the equation.
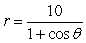
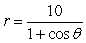

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
65
Identify the conic (parabola, ellipse, or hyperbola) that is represented by the equation.
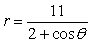
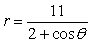

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
66
Identify the conic (parabola, ellipse, or hyperbola) that is represented by the equation.
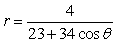
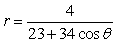

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
67
Identify the conic (parabola, ellipse, or hyperbola) that is represented by the equation.
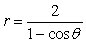
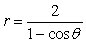

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
68
Identify the conic (parabola, ellipse, or hyperbola) that is represented by the equation.
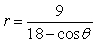
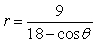

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
69
Identify the conic (parabola, ellipse, or hyperbola) that is represented by the equation.
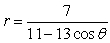
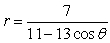

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
70
(a) Identify the type of conic by the discriminant, (b) transform the equation in x and y into an equation in X and Y (without an XY term) by rotating the x- and y-axes by an angle of θ to arrive at the new X- and Y-axes, and (c) graph the resulting equation (showing both sets of axes).
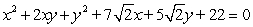
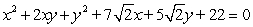

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
71
(a) Identify the type of conic by the discriminant, (b) transform the equation in x and y into an equation in X and Y (without an XY term) by rotating the x- and y-axes by an angle of θ to arrive at the new X- and Y-axes, and (c) graph the resulting equation (showing both sets of axes).
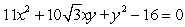
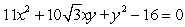

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
72
If the xy-coordinate axes are rotated 45°, find the XY coordinates of the point (x, y) = (3, -6).

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
73
If the xy-coordinate axes are rotated 30°, find the XY coordinates of the point (x, y) =
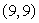
.
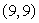
.

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
74
If the xy-coordinate axes are rotated 60°, find the XY coordinates of the point (x, y) =
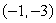
.
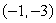
.

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
75
If the xy-coordinate axes are rotated 45°, find the XY coordinates of the point (x, y) = (-33, 3).

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
76
If the xy-coordinate axes are rotated 30°, find the XY coordinates of the point (x, y) =
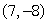
.
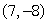
.

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
77
If the xy-coordinate axes are rotated 60°, find the XY coordinates of the point (x, y) =
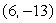
.
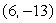
.

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
78
Determine the angle of rotation necessary to transform the equation in x and y into an equation in X and Y with no XY term. Round to one decimal place.
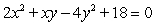
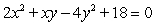

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
79
(a) Identify the type of conic by the discriminant, (b) transform the equation in x and y into an equation in X and Y (without an XY term) by rotating the x- and y-axes by an angle of θ to arrive at the new X- and Y-axes, and (c) graph the resulting equation (showing both sets of axes).
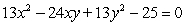
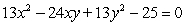

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck
80
Graph the second-degree equation. (Hint: Transform the equation into an equation that contains no xy term).
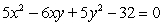
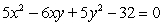

Unlock Deck
Unlock for access to all 230 flashcards in this deck.
Unlock Deck
k this deck


