Deck 7: Vectors, the Complex Plane, and Polar Coordinates
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/225
Play
Full screen (f)
Deck 7: Vectors, the Complex Plane, and Polar Coordinates
1
Convert the point to exact polar coordinates. Assume 0 ≤ θ ≤ 2π.
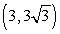
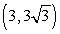
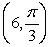
2
Convert the point to exact polar coordinates. Assume 0 ≤ θ ≤ 2π.
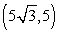
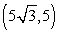
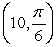
3
Convert the point to exact polar coordinates. Assume 0 ≤ θ ≤ 2π.
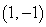
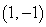
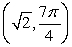
4
Convert the point to exact polar coordinates. Assume 0 ≤ θ ≤ 2π.
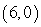
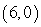

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
5
Convert the point to exact rectangular coordinates.
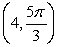
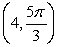

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
6
Convert the point to exact rectangular coordinates.
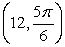
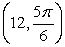

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
7
Convert the point to exact rectangular coordinates.
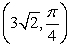
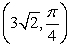

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
8
Convert the point to exact rectangular coordinates.
(2, /2)
(2, /2)

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
9
Convert the point to exact rectangular coordinates.
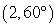
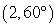

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
10
Convert the point to exact rectangular coordinates.
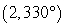
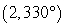

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
11
Convert the point to exact rectangular coordinates.
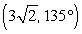
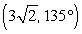

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
12
Graph the equation.
r = cos 2 θ
r = cos 2 θ

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
13
Graph the equation.
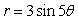
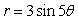

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
14
Graph the equation.
r2 = 4 cos 5θ
r2 = 4 cos 5θ

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
15
Graph the equation.
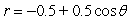
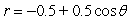

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
16
Graph the equation.
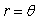
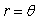

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
17
Spirals are seen in nature - in the swirl of a pine cone; they are also used in machinery to convert motions. An Archimedes Spiral has the general equation r = a θ. A more general form for the quation of a spiral is r = aθ1/n where n is a constant that determines how tightly the spiral is wrapped. Compare the Archimedes Sprial r = θ with the spiral
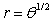
by graphing both on the same polar graph.
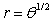
by graphing both on the same polar graph.

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
18
The lemniscate motion occurs naturally in the flapping of birds' wings. The bird's vertical lift and wing sweep create the distinctive figure-eight pattern. The patterns vary with the different wing profiles. Compare the two possible lemniscate patterns by graphing them on the same polar graph: r2 = cos 2θ and r2 = cos (2θ + 1).

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
19
Many microphones advertise that their exceptional pickup capabilities hat isolate the sound source and minimize background noise. The name of these microphones comes from the pattern formed by the range of the pickup. Graph the cardioid curve to see what the range looks like.
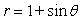
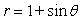

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
20
Convert the point to exact polar coordinates. Assume 0 2 . 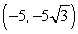
A)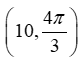
B)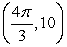
C)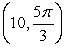
D)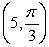
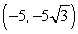
A)
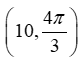
B)
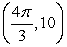
C)
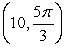
D)
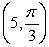

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
21
Convert the point to exact polar coordinates. Assume 0 2 . 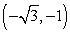
A)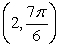
B)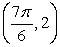
C)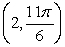
D)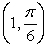
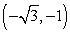
A)
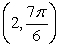
B)
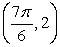
C)
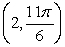
D)
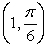

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
22
Convert the point to exact polar coordinates. Assume 0 2 . 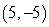
A)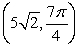
B)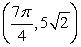
C)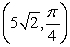
D)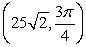
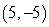
A)
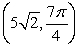
B)
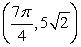
C)
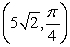
D)
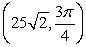

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
23
Convert the point to exact polar coordinates. Assume 0 2 . 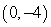
A) (4, 3 /2)
B) (3 /2, 4)
C) (-4, 3 /2)
D) (16, )
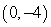
A) (4, 3 /2)
B) (3 /2, 4)
C) (-4, 3 /2)
D) (16, )

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
24
Convert the point to exact rectangular coordinates. 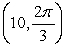
A)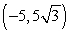
B)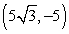
C)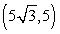
D)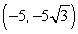
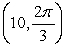
A)
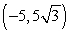
B)
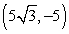
C)
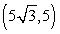
D)
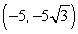

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
25
Convert the point to exact rectangular coordinates. 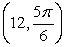
A)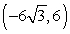
B)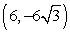
C)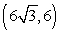
D)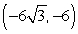
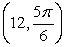
A)
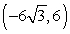
B)
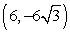
C)
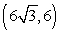
D)
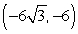

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
26
Convert the point to exact rectangular coordinates. 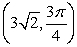
A)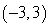
B)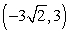
C)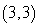
D)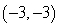
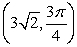
A)
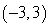
B)
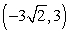
C)
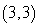
D)
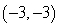

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
27
Convert the point to exact rectangular coordinates.
(1, )
A)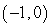
B)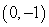
C)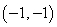
D)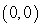
(1, )
A)
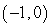
B)
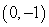
C)
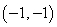
D)
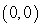

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
28
Convert the point to exact rectangular coordinates. 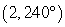
A)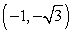
B)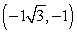
C)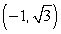
D)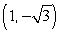
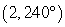
A)
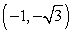
B)
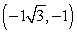
C)
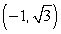
D)
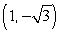

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
29
Convert the point to exact rectangular coordinates. 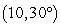
A)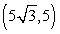
B)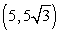
C)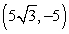
D)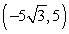
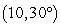
A)
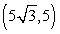
B)
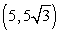
C)
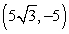
D)
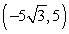

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
30
Convert the point to exact rectangular coordinates. 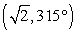
A)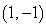
B)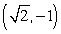
C)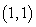
D)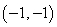
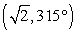
A)
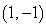
B)
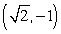
C)
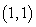
D)
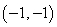

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
31
Graph the equation. 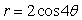
A)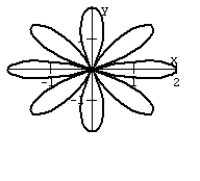
B)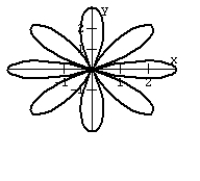
C)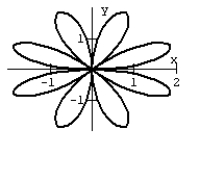
D)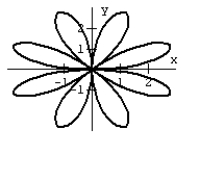
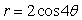
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
32
Graph the equation. 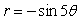
A)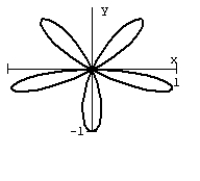
B)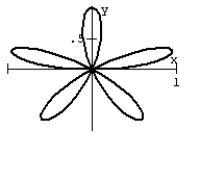
C)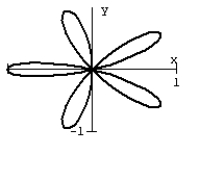
D)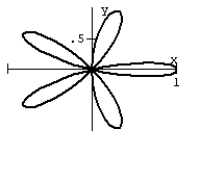
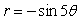
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
33
Graph the equation.
R2 = cos 5
A)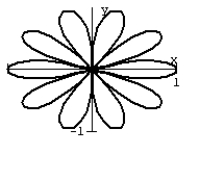
B)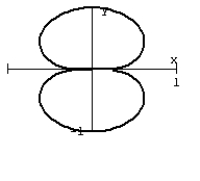
C)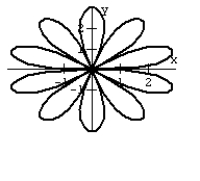
D)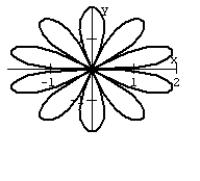
R2 = cos 5
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
34
Graph the equation. 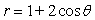
A)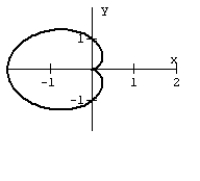
B)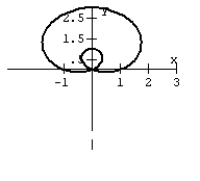
C)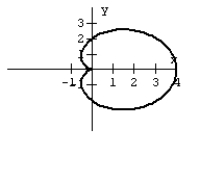
D)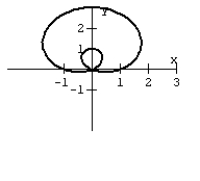
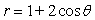
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
35
Graph the equation. 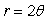
A)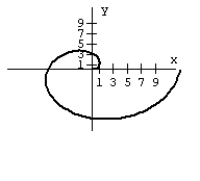
B)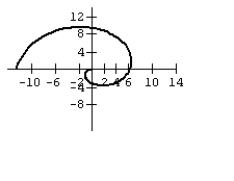
C)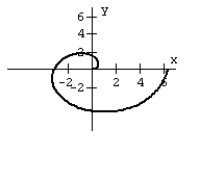
D)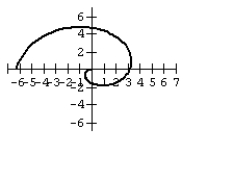
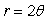
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
36
The lemniscate motion occurs naturally in the flapping of birds' wings. The bird's vertical lift and wing sweep create the distinctive figure-eight pattern. The patterns vary with the different wing profiles. Compare the two possbile lemniscate patterns by graphing them on the same polar graph: r2 = cos 2 and r2 = cos (2 + 2).
A)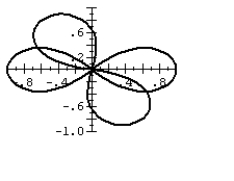
B)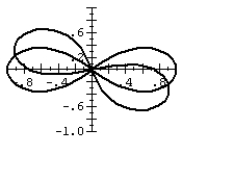
C)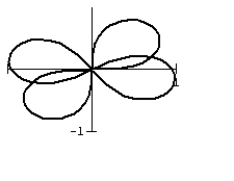
D)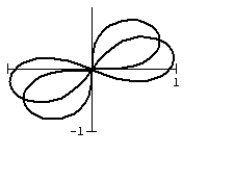
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
37
Many microphones advertise that their exceptional pickup capabilities hat isolate the sound source and minimize background noise. The name of these microphones comes from the pattern formed by the range of the pickup. Graph the cardioid curve to see what the range looks like. 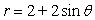
A)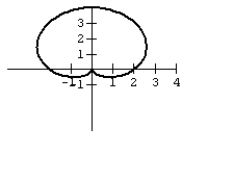
B)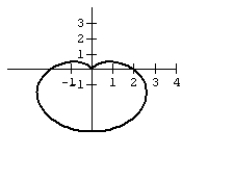
C)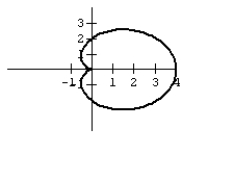
D)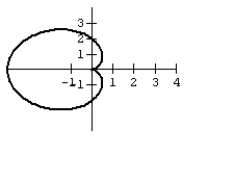
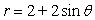
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
38
Plot the point
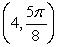
in a polar coordinate system.
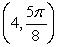
in a polar coordinate system.

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
39
Plot the point
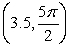
in a polar coordinate system.
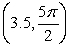
in a polar coordinate system.

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
40
Plot the point
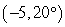
in a polar coordinate system.
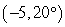
in a polar coordinate system.

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
41
Convert the equation
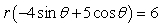
from polar to rectangular form.
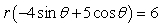
from polar to rectangular form.

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
42
Convert the equation
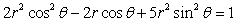
from polar to rectangular form.
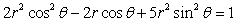
from polar to rectangular form.

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
43
Convert the equation
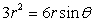
from polar to rectangular form.
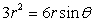
from polar to rectangular form.

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
44
Find the product, z1z2 in rectangular form.
z1 = 3 [ cos 225° + i sin 225° ] and z2 = 16 [ cos 15° + i sin 15° ]
z1 = 3 [ cos 225° + i sin 225° ] and z2 = 16 [ cos 15° + i sin 15° ]

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
45
Find the product, z1z2 in rectangular form.
z1 = 2 [ cos 84° + i sin 84° ] and z2 = 12 [ cos 66° + i sin 66° ]
z1 = 2 [ cos 84° + i sin 84° ] and z2 = 12 [ cos 66° + i sin 66° ]

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
46
Find the product, z1z2 in rectangular form.
z1 = 3 [ cos 197° + i sin 197° ] and z2 = 10 [ cos 28° + i sin 28° ]
z1 = 3 [ cos 197° + i sin 197° ] and z2 = 10 [ cos 28° + i sin 28° ]

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
47
Find the product, z1z2 in rectangular form.
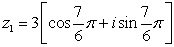 and
and 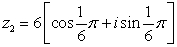
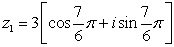 and
and 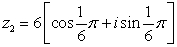

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
48
Find the product, z1z2 in rectangular form.
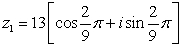 and
and 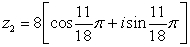
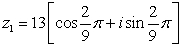 and
and 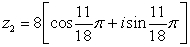

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
49
Find the product, z1z2 in rectangular form.
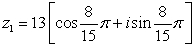 and
and 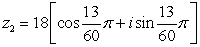
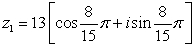 and
and 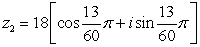

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
50
Find the quotient,
![Find the quotient, in rectangular form. z<sub>1</sub> = 24 [ cos 78° + i sin 78° ] and z<sub>2</sub> = 4 [ cos 18° + i sin 18° ]](https://storage.examlex.com/TB10663/11eed1b2_576e_ffa2_a8a5_a1dc21eba800_TB10663_00.jpg)
in rectangular form.
z1 = 24 [ cos 78° + i sin 78° ] and z2 = 4 [ cos 18° + i sin 18° ]
![Find the quotient, in rectangular form. z<sub>1</sub> = 24 [ cos 78° + i sin 78° ] and z<sub>2</sub> = 4 [ cos 18° + i sin 18° ]](https://storage.examlex.com/TB10663/11eed1b2_576e_ffa2_a8a5_a1dc21eba800_TB10663_00.jpg)
in rectangular form.
z1 = 24 [ cos 78° + i sin 78° ] and z2 = 4 [ cos 18° + i sin 18° ]

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
51
Find the quotient,
![Find the quotient, in rectangular form. z<sub>1</sub> = 104 [ cos 173° + i sin 173° ] and z<sub>2</sub> = 4 [ cos 23° + i sin 23° ]](https://storage.examlex.com/TB10663/11eed1b2_576e_ffa4_a8a5_556754e2fa81_TB10663_00.jpg)
in rectangular form.
z1 = 104 [ cos 173° + i sin 173° ] and z2 = 4 [ cos 23° + i sin 23° ]
![Find the quotient, in rectangular form. z<sub>1</sub> = 104 [ cos 173° + i sin 173° ] and z<sub>2</sub> = 4 [ cos 23° + i sin 23° ]](https://storage.examlex.com/TB10663/11eed1b2_576e_ffa4_a8a5_556754e2fa81_TB10663_00.jpg)
in rectangular form.
z1 = 104 [ cos 173° + i sin 173° ] and z2 = 4 [ cos 23° + i sin 23° ]

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
52
Find the quotient,
![Find the quotient, in rectangular form. z<sub>1</sub> = 208 [ cos 180° + i sin 180° ] and z<sub>2</sub> = 8 [ cos 45° + i sin 45° ]](https://storage.examlex.com/TB10663/11eed1b2_576e_ffa6_a8a5_9dc798419b11_TB10663_00.jpg)
in rectangular form.
z1 = 208 [ cos 180° + i sin 180° ] and z2 = 8 [ cos 45° + i sin 45° ]
![Find the quotient, in rectangular form. z<sub>1</sub> = 208 [ cos 180° + i sin 180° ] and z<sub>2</sub> = 8 [ cos 45° + i sin 45° ]](https://storage.examlex.com/TB10663/11eed1b2_576e_ffa6_a8a5_9dc798419b11_TB10663_00.jpg)
in rectangular form.
z1 = 208 [ cos 180° + i sin 180° ] and z2 = 8 [ cos 45° + i sin 45° ]

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
53
Find the quotient,
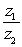
in rectangular form.
and
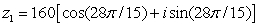
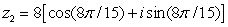
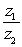
in rectangular form.
and
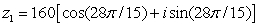
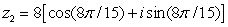

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
54
Find the quotient,
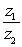
in rectangular form.
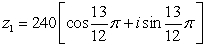 and
and
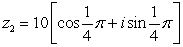
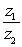
in rectangular form.
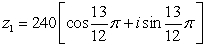 and
and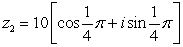

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
55
Find the quotient,
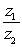
in rectangular form.
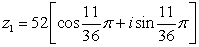 and
and
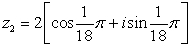
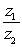
in rectangular form.
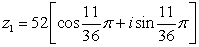 and
and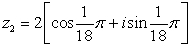

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
56
Find the result of the expression using De Moivre's theorem. Write the answer in rectangular form.
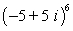
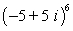

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
57
Find the result of the expression using De Moivre's theorem. Write the answer in rectangular form.
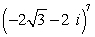
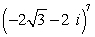

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
58
Find the result of the expression using De Moivre's theorem. Write the answer in rectangular form.
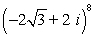
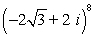

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
59
Find the result of the expression using De Moivre's theorem. Write the answer in rectangular form.
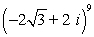
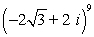

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
60
Find the result of the expression using De Moivre's theorem. Write the answer in rectangular form.
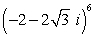
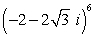

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
61
Find all nth roots of z. Write answers in polar form and plot roots in complex plane.
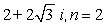
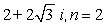

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
62
Find all nth roots of z. Write answers in polar form and plot roots in complex plane.
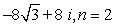
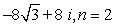

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
63
Find all nth roots of z. Write answers in polar form and plot roots in complex plane.
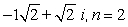
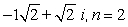

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
64
Find all nth roots of z. Write answers in polar form.
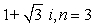
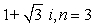

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
65
Find all nth roots of z. Write answers in polar form.
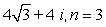
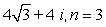

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
66
Find all nth roots of z. Write answers in polar form.
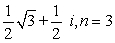
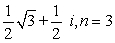

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
67
Find all nth roots of z. Write answers in polar form.
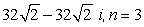
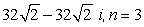

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
68
Find all nth roots of z. Write answers in polar form.
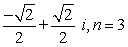
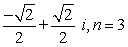

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
69
Find all nth roots of z. Write answers in polar form.



Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
70
Find all nth roots of z. Write answers in polar form.
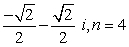
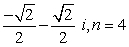

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
71
Find all complex solutions to the equation.Write answers in rectangular form.
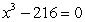
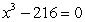

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
72
Find all complex solutions to the equation.Write answers in rectangular form.
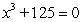
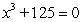

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
73
Find all complex solutions to the equation.Write answers in rectangular form.
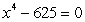
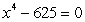

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
74
Find all complex solutions to the equation.Write answers in rectangular form.
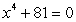
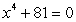

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
75
Find all complex solutions to the equation.Write answers in rectangular form.
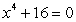
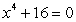

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
76
Find all complex solutions to the equation.Write answers in rectangular form.
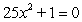
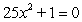

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
77
Find all complex solutions to the equation.
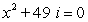
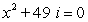

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
78
When you graph the five fifth roots of
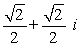
and connect the points, you form a pentagon. Find the roots and draw the pentagon.
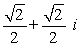
and connect the points, you form a pentagon. Find the roots and draw the pentagon.

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
79
Find the product, z1z2 in rectangular form.
Z1 = 8 [ cos 23° + i sin 23° ] and z2 = 4 [ cos 37° + i sin 37° ]
A)![<strong>Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form. Z<sub>1</sub> = 8 [ cos 23° + i sin 23° ] and z<sub>2</sub> = 4 [ cos 37° + i sin 37° ]</strong> A) B) C) D)](https://storage.examlex.com/TB10663/11eed1b2_5770_fbb8_a8a5_eb7062343f8f_TB10663_00.jpg)
B)![<strong>Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form. Z<sub>1</sub> = 8 [ cos 23° + i sin 23° ] and z<sub>2</sub> = 4 [ cos 37° + i sin 37° ]</strong> A) B) C) D)](https://storage.examlex.com/TB10663/11eed1b2_5770_fbb9_a8a5_4d70039ae8b5_TB10663_00.jpg)
C)![<strong>Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form. Z<sub>1</sub> = 8 [ cos 23° + i sin 23° ] and z<sub>2</sub> = 4 [ cos 37° + i sin 37° ]</strong> A) B) C) D)](https://storage.examlex.com/TB10663/11eed1b2_5770_fbba_a8a5_d5b7f5efa67e_TB10663_00.jpg)
D)![<strong>Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form. Z<sub>1</sub> = 8 [ cos 23° + i sin 23° ] and z<sub>2</sub> = 4 [ cos 37° + i sin 37° ]</strong> A) B) C) D)](https://storage.examlex.com/TB10663/11eed1b2_5770_fbbb_a8a5_11f12887890d_TB10663_00.jpg)
Z1 = 8 [ cos 23° + i sin 23° ] and z2 = 4 [ cos 37° + i sin 37° ]
A)
![<strong>Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form. Z<sub>1</sub> = 8 [ cos 23° + i sin 23° ] and z<sub>2</sub> = 4 [ cos 37° + i sin 37° ]</strong> A) B) C) D)](https://storage.examlex.com/TB10663/11eed1b2_5770_fbb8_a8a5_eb7062343f8f_TB10663_00.jpg)
B)
![<strong>Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form. Z<sub>1</sub> = 8 [ cos 23° + i sin 23° ] and z<sub>2</sub> = 4 [ cos 37° + i sin 37° ]</strong> A) B) C) D)](https://storage.examlex.com/TB10663/11eed1b2_5770_fbb9_a8a5_4d70039ae8b5_TB10663_00.jpg)
C)
![<strong>Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form. Z<sub>1</sub> = 8 [ cos 23° + i sin 23° ] and z<sub>2</sub> = 4 [ cos 37° + i sin 37° ]</strong> A) B) C) D)](https://storage.examlex.com/TB10663/11eed1b2_5770_fbba_a8a5_d5b7f5efa67e_TB10663_00.jpg)
D)
![<strong>Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form. Z<sub>1</sub> = 8 [ cos 23° + i sin 23° ] and z<sub>2</sub> = 4 [ cos 37° + i sin 37° ]</strong> A) B) C) D)](https://storage.examlex.com/TB10663/11eed1b2_5770_fbbb_a8a5_11f12887890d_TB10663_00.jpg)

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck
80
Find the product, z1z2 in rectangular form.
Z1 = 10 [ cos 306° + i sin 306° ] and z2 = 18 [ cos 24° + i sin 24° ]
A)![<strong>Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form. Z<sub>1</sub> = 10 [ cos 306° + i sin 306° ] and z<sub>2</sub> = 18 [ cos 24° + i sin 24° ]</strong> A) B) C) D)](https://storage.examlex.com/TB10663/11eed1b2_5770_fbbc_a8a5_bf179278478a_TB10663_00.jpg)
B)![<strong>Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form. Z<sub>1</sub> = 10 [ cos 306° + i sin 306° ] and z<sub>2</sub> = 18 [ cos 24° + i sin 24° ]</strong> A) B) C) D)](https://storage.examlex.com/TB10663/11eed1b2_5770_fbbd_a8a5_f9dd64c5fcbb_TB10663_00.jpg)
C)![<strong>Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form. Z<sub>1</sub> = 10 [ cos 306° + i sin 306° ] and z<sub>2</sub> = 18 [ cos 24° + i sin 24° ]</strong> A) B) C) D)](https://storage.examlex.com/TB10663/11eed1b2_5770_fbbe_a8a5_b7dc2b49702c_TB10663_00.jpg)
D)![<strong>Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form. Z<sub>1</sub> = 10 [ cos 306° + i sin 306° ] and z<sub>2</sub> = 18 [ cos 24° + i sin 24° ]</strong> A) B) C) D)](https://storage.examlex.com/TB10663/11eed1b2_5770_fbbf_a8a5_1df9800d3837_TB10663_00.jpg)
Z1 = 10 [ cos 306° + i sin 306° ] and z2 = 18 [ cos 24° + i sin 24° ]
A)
![<strong>Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form. Z<sub>1</sub> = 10 [ cos 306° + i sin 306° ] and z<sub>2</sub> = 18 [ cos 24° + i sin 24° ]</strong> A) B) C) D)](https://storage.examlex.com/TB10663/11eed1b2_5770_fbbc_a8a5_bf179278478a_TB10663_00.jpg)
B)
![<strong>Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form. Z<sub>1</sub> = 10 [ cos 306° + i sin 306° ] and z<sub>2</sub> = 18 [ cos 24° + i sin 24° ]</strong> A) B) C) D)](https://storage.examlex.com/TB10663/11eed1b2_5770_fbbd_a8a5_f9dd64c5fcbb_TB10663_00.jpg)
C)
![<strong>Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form. Z<sub>1</sub> = 10 [ cos 306° + i sin 306° ] and z<sub>2</sub> = 18 [ cos 24° + i sin 24° ]</strong> A) B) C) D)](https://storage.examlex.com/TB10663/11eed1b2_5770_fbbe_a8a5_b7dc2b49702c_TB10663_00.jpg)
D)
![<strong>Find the product, z<sub>1</sub>z<sub>2</sub> in rectangular form. Z<sub>1</sub> = 10 [ cos 306° + i sin 306° ] and z<sub>2</sub> = 18 [ cos 24° + i sin 24° ]</strong> A) B) C) D)](https://storage.examlex.com/TB10663/11eed1b2_5770_fbbf_a8a5_1df9800d3837_TB10663_00.jpg)

Unlock Deck
Unlock for access to all 225 flashcards in this deck.
Unlock Deck
k this deck


