Deck 4: Trigonometric Functions of Angles
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/261
Play
Full screen (f)
Deck 4: Trigonometric Functions of Angles
1
Solve the given triangle. Round angle to one decimal place and side measures to 3 significant digits.
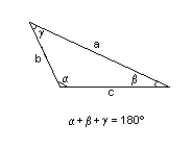
b = 246 yd., c = 377 yd. , a = 426 yd.

b = 246 yd., c = 377 yd. , a = 426 yd.
= 35.0°, = 61.4, = 83.6°
2
Solve the given triangle. Round angle to one decimal place and side measures to 3 significant digits.
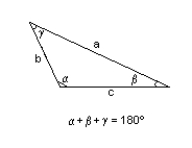
b = 63 in., = 48.4°, a = 56.6 in.

b = 63 in., = 48.4°, a = 56.6 in.
= 72.6°, = 59.0°, c = 49.4 in.
3
Solve the given triangle. Round angle to one decimal place and side measures to 3 significant digits.
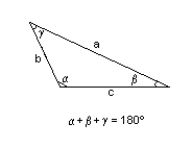
C = 199 yd., a = 232 yd. , b = 219 yd.
A) = 52.2°, = 67.2°, = 60.6°
B) = 60.6°, = 52.2°, = 67.2°
C) = 67.2°, = 60.6°, = 52.2°
D) no solution

C = 199 yd., a = 232 yd. , b = 219 yd.
A) = 52.2°, = 67.2°, = 60.6°
B) = 60.6°, = 52.2°, = 67.2°
C) = 67.2°, = 60.6°, = 52.2°
D) no solution
= 52.2°, = 67.2°, = 60.6°
4
Solve the given triangle. Round angle to one decimal place and side measures to 3 significant digits.
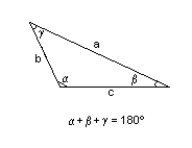
B = 94 ft., = 45.8°, a = 89.5 ft.
A) = 70.4°, = 63.8°, c = 71.5 ft.
B) = 63.8°, = 70.4°, c = 97 ft.
C) = 70.4°, = 63.8°, c = 106 ft.
D) no solution

B = 94 ft., = 45.8°, a = 89.5 ft.
A) = 70.4°, = 63.8°, c = 71.5 ft.
B) = 63.8°, = 70.4°, c = 97 ft.
C) = 70.4°, = 63.8°, c = 106 ft.
D) no solution

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
5
A plane flew due north at 460 mph for 3.5 hours. A second plane, starting at the same point and at the same time flew southeast at an angle 140° clockwise from due north for 3.5 hours. If, at the end of the 3.5 hours, the two planes were 2550 miles apart, how fast was the second plane traveling?

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
6
A 26 foot slide leaning against the bottom of a building's window makes a 57° angle with the building. The angle formed with the building with the line of sight from the top of the window to the point on the ground where the slide ends is 39°. How tall is the window? Round to the nearest integer.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
7
An airplane door is 5 feet high. If a slide attached to the bottom of the open door is at an angle of 28° with the ground, and the angle formed by the line of sight from where the slide touches the ground to the top of the door is 39°, then how long is the slide?

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
8
A plane flew due north at 380 mph for 4 hours. A second plane, starting at the same point and at the same time flew southeast at an angle 168° clockwise from due north for 4 hours. If, at the end of the 4 hours, the two planes were 2300 miles apart, how fast was the second plane traveling?
A) 18.3 mph
B) 772 mph
C) 193 mph
D) no solution
A) 18.3 mph
B) 772 mph
C) 193 mph
D) no solution

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
9
A 36 foot slide leaning against the bottom of a building's window makes a 52° angle with the building. The angle formed with the building with the line of sight from the top of the window to the point on the ground where the slide ends is 39°. How tall is the window? Round to the nearest integer.
A) 46 feet
B) 13 feet
C) 127 feet
D) no solution
A) 46 feet
B) 13 feet
C) 127 feet
D) no solution

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
10
An airplane door is 5 feet high. If a slide attached to the bottom of the open door is at an angle of 40° with the ground, and the angle formed by the line of sight from where the slide touches the ground to the top of the door is 50°, then how long is the slide?
A) 19 feet
B) 22 feet
C) 6 feet
D) no solution
A) 19 feet
B) 22 feet
C) 6 feet
D) no solution

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
11
Find the area of the triangle described. Round to the nearest integer.
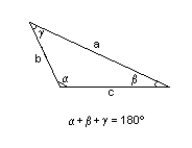
b = 370, c = 439, = 36

b = 370, c = 439, = 36

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
12
Find the area of the triangle described. Round to the nearest integer.
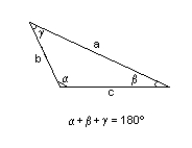
c = 428, a = 416 , b = 120

c = 428, a = 416 , b = 120

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
13
A parking lot is to have the shape of a parallelogram that has adjacent sides measuring 158 feet and 277 feet. The angle between the two sides is 43°. What is the area of the parking lot? Round to the nearest integer.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
14
A regular heptagon has sides measuring 36 feet. What is its area? (Hint: The measure of an angle of a regular n-gon is equal to 180(n - 2) divided by the number of sides, n.) Round to one decimal place.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
15
Find the area of the triangle described. Round to the nearest integer.
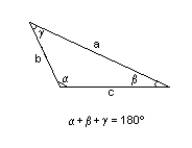
A = 274, b = 257, = 29°
A) 17,070
B) 34,139
C) 23,366
D) no solution

A = 274, b = 257, = 29°
A) 17,070
B) 34,139
C) 23,366
D) no solution

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
16
Find the area of the triangle described. Round to the nearest integer.
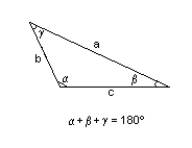
B = 493, c = 402 , a = 338
A) 67,441
B) 4,548,335,944
C) 823,777
D) 815,453

B = 493, c = 402 , a = 338
A) 67,441
B) 4,548,335,944
C) 823,777
D) 815,453

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
17
A parking lot is to have the shape of a parallelogram that has adjacent sides measuring 281 feet and 253 feet. The angle between the two sides is 57°. What is the area of the parking lot? Round to the nearest integer.
A) 59,624 square feet
B) 29,812 square feet
C) 31,008 square feet
D) 38,720 square feet
A) 59,624 square feet
B) 29,812 square feet
C) 31,008 square feet
D) 38,720 square feet

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
18
A regular decagon has sides measuring 38 inches. What is its area? (Hint: The measure of an angle of a regular n-gon is equal to 180(n - 2) divided by the number of sides, n.) Round to one decimal place.
A) 11110.4 square inches
B) 3795.8 square inches
C) 4968.7 square inches
D) 11682.2 square inches
A) 11110.4 square inches
B) 3795.8 square inches
C) 4968.7 square inches
D) 11682.2 square inches

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
19
Peg and Meg live five miles apart. The school that they attend lies on a street that makes a 34° angle with the street connecting their houses when measured from Peg's house. The street connecting Meg's house and the school makes a 38° angle with the street connecting them. How far is it from Peg's house to the school?

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
20
Decide whether the Law of Cosines is needed to solve this triangle.
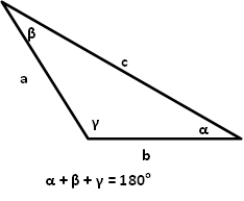
Given: sides a and b, and angle
A) Do NOT need Law of Cosines
B) Do need Law of Cosines

Given: sides a and b, and angle
A) Do NOT need Law of Cosines
B) Do need Law of Cosines

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
21
Find the area of the triangle described. Round to three decimal places.
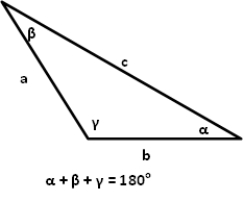
b =
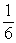
, c =
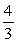
, = 54

b =
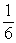
, c =
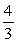
, = 54

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
22
Find the area of the triangle described. Round to one decimal place.
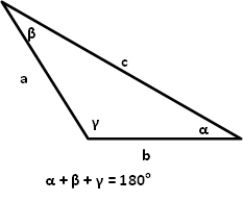
a =
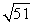
, b = 38 , c = 39

a =
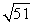
, b = 38 , c = 39

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
23
Some very destructive beetles have made their way into a forest preserve. The rangers are trying to keep track of their spread and how well preventative measures are working. In a triangular area that is 49.9 miles on one side, 43.5 miles on another and 57.0 miles on the third, what is the total area the rangers are covering? Round to one decimal place.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
24
A real estate agent needs to determine the area of a triangular lot. Two sides of the lot are 130 feet and 100 feet. The angle between the two measured sides is 79°. What is the area of the lot? Round to one decimal place.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
25
Big Augie's Pizza now offers equilateral triangle shaped pizzas. How long must the sides of the pizza be to the nearest inch to equal the size of a round pizza with a 17 inch diameter?

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
26
Classify the triangle as AAS, SAS, SSA, SAS, or SSS given the following information.
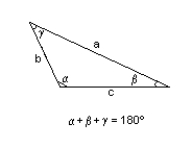 b, c
b, c
 b, c
b, c 
Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
27
Classify the triangle as AAS, SAS, SSA, SAS, or SSS given the following information.
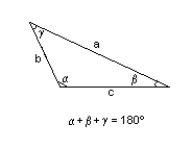 c
c
 c
c 
Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
28
Solve the given triangle. Round angle to one decimal place and side measures to 3 significant digits.
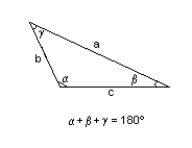
b = 142 yd., = 54.2°, = 60.4°

b = 142 yd., = 54.2°, = 60.4°

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
29
Solve the given triangle. Round angle to one decimal place and side measures to 3 significant digits.
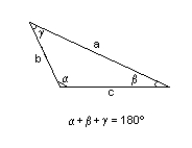
b = 217 yd., = 54.2°, = 37.0°

b = 217 yd., = 54.2°, = 37.0°

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
30
Solve the given triangle. Round angles to one decimal place and side measure to 3 significant figures.
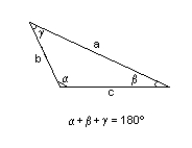
c = 151 cm., a = 55 cm., = 69.0°

c = 151 cm., a = 55 cm., = 69.0°

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the given triangle. Round angles to one decimal place and side measures to 3 significant figures.
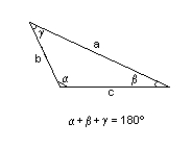
b = 67 yd., c = 70.3 yd., = 70.0°

b = 67 yd., c = 70.3 yd., = 70.0°

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
32
Solve the given triangle and round to one decimal place.
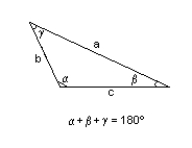
A = 151.0 yd., = 69.0°, = 63.4°
A) = 47.6°, b = 144.6 yd. , c = 119.4 yd.
B) = 47.6°, b = 119.4 yd. , c = 144.6 yd.
C) = 47.6°, b = 157.7 yd. , c = 124.7 yd.
D) = 47.6°, b = 190.9 yd. , c = 182.8 yd.

A = 151.0 yd., = 69.0°, = 63.4°
A) = 47.6°, b = 144.6 yd. , c = 119.4 yd.
B) = 47.6°, b = 119.4 yd. , c = 144.6 yd.
C) = 47.6°, b = 157.7 yd. , c = 124.7 yd.
D) = 47.6°, b = 190.9 yd. , c = 182.8 yd.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the given triangle and round to one decimal place.
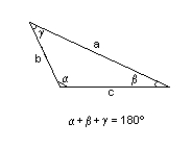
B = 57.0 cm., = 61.8°, = 63.4°
A) = 54.8°, c = 61.5 cm. , a = 62.4 cm.
B) = 54.8°, c = 62.4 cm. , a = 61.5 cm.
C) = 54.8°, c = 52.9 cm. , a = 57.8 cm.
D) = 54.8°, c = 52.1 cm. , a = 57.0 cm.

B = 57.0 cm., = 61.8°, = 63.4°
A) = 54.8°, c = 61.5 cm. , a = 62.4 cm.
B) = 54.8°, c = 62.4 cm. , a = 61.5 cm.
C) = 54.8°, c = 52.9 cm. , a = 57.8 cm.
D) = 54.8°, c = 52.1 cm. , a = 57.0 cm.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the given triangle and round to one decimal place.
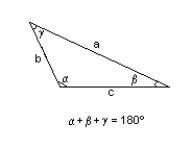
B = 199.0 cm., c = 45.0 cm., = 40.0°
A) = 8.4°, = 131.6°, a = 231.4 cm.
B) = 131.6°, = 8.4°, a = 231.4 cm.
C) = 8.4°, = 131.6°, a = 171.2 cm.
D) no solution

B = 199.0 cm., c = 45.0 cm., = 40.0°
A) = 8.4°, = 131.6°, a = 231.4 cm.
B) = 131.6°, = 8.4°, a = 231.4 cm.
C) = 8.4°, = 131.6°, a = 171.2 cm.
D) no solution

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
35
Solve the given triangle and round to one decimal place.
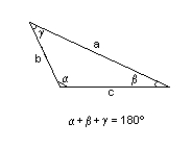
B = 33.0 in., c = 35.8 in., = 30.0°
A) Case one: 1 = 32.8°, 1 = 117.2°, a1 = 58.7 in.
Case two: 2 = 147.2°, 2 = 2.8°, a2 = 3.3 in.
B) Case one: 1 = 32.8°, 1 = 117.2°, a1 = 58.7 in.
Case two: 2 = 2.8°, 2 = 147.2°, a2 = 3.3 in.
C) = 32.8°, = 117.2°, a = 58.7 in. and no ambiguous case
D) no solution

B = 33.0 in., c = 35.8 in., = 30.0°
A) Case one: 1 = 32.8°, 1 = 117.2°, a1 = 58.7 in.
Case two: 2 = 147.2°, 2 = 2.8°, a2 = 3.3 in.
B) Case one: 1 = 32.8°, 1 = 117.2°, a1 = 58.7 in.
Case two: 2 = 2.8°, 2 = 147.2°, a2 = 3.3 in.
C) = 32.8°, = 117.2°, a = 58.7 in. and no ambiguous case
D) no solution

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
36
A hot air balloon is sighted at the same time by two friends who are 2.2 miles apart on the same side of the balloon. The angles of elevation from the two friends are 11.5° and 18°. How high is the balloon? Round to one decimal place.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
37
A tracking station has two telescopes that are 1.6 miles apart. The telescopes can lock onto a rocket after it is launched and record the angles of elevation to the rocket. If the angles of elevation from telescope A and B are 27° and 56°, respectively, then how far is the rocket from telescope A? Round to one decimal place.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
38
An engineer wants to construct a bridge across a fast moving river. Using a straight line segment between two points that are 187 feet apart along his side of the river, he measures the angles formed when sighting the point on the other side where he wants to have the bridge end. If the angles formed at points A and B are 68° and 34°, respectively, how far is it from point B to the point on the other side of the river? Round to one decimal place.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
39
A hot air balloon is sighted at the same time by two friends who are 2.5 miles apart on the same side of the balloon. The angles of elevation from the two friends are 20.5° and 28°. How high is the balloon? Round to one decimal place.
A) 3.1 miles
B) 0.2 mile
C) 0.4 mile
D) no solution
A) 3.1 miles
B) 0.2 mile
C) 0.4 mile
D) no solution

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
40
A tracking station has two telescopes that are 1.7 miles apart. The telescopes can lock onto a rocket after it is launched and record the angles of elevation to the rocket. If the angles of elevation from telescope A and B are 22.5° and 44°, respectively, then how far is the rocket from telescope B? Round to one decimal place.
A) 1.8 miles
B) 3.2 miles
C) 1.6 miles
D) no solution
A) 1.8 miles
B) 3.2 miles
C) 1.6 miles
D) no solution

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
41
An engineer wants to construct a bridge across a fast moving river. Using a straight line segment between two points that are 95 feet apart along his side of the river, he measures the angles formed when sighting the point on the other side where he wants to have the bridge end. If the angles formed at points A and B are 78° and 37°, respectively, how far is it from point A to the point on the other side of the river? Round to one decimal place.
A) 63.1 feet
B) 102.5 feet
C) 143.1 feet
D) no solution
A) 63.1 feet
B) 102.5 feet
C) 143.1 feet
D) no solution

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
42
The terminal side of an angle θ in standard position passes through the point
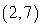
. Calculate the exact value of sin θ.
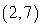
. Calculate the exact value of sin θ.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
43
The terminal side of an angle θ in standard position passes through the point
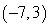
. Calculate the exact value of csc θ.
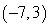
. Calculate the exact value of csc θ.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
44
The terminal side of an angle θ in standard position passes through the point
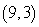
. Calculate the exact value of cot θ.
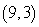
. Calculate the exact value of cot θ.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
45
The terminal side of an angle θ in standard position passes through the point
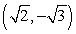
. Calculate the exact value of sin θ.
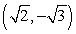
. Calculate the exact value of sin θ.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
46
The terminal side of an angle θ in standard position passes through the point
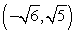
. Calculate the exact value of cot θ.
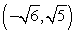
. Calculate the exact value of cot θ.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
47
The terminal side of an angle θ in standard position passes through the point
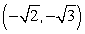
. Calculate the exact value of sec θ.
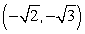
. Calculate the exact value of sec θ.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
48
The terminal side of an angle θ in standard position passes through the point
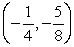
. Calculate the value of sin θ.
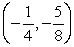
. Calculate the value of sin θ.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
49
The terminal side of an angle θ in standard position passes through the point
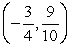
. Calculate the value of cos θ.
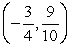
. Calculate the value of cos θ.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
50
The terminal side of an angle θ in standard position passes through the point
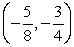
. Calculate the value of tan θ.
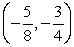
. Calculate the value of tan θ.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
51
The terminal side of an angle θ in standard position passes through the point
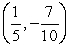
. Calculate the value of cot θ.
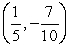
. Calculate the value of cot θ.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
52
The terminal side of an angle θ in standard position passes through the point
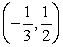
. Calculate the value of csc θ.
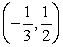
. Calculate the value of csc θ.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
53
The terminal side of an angle θ in standard position passes through the point
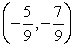
. Calculate the value of sec θ.
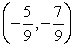
. Calculate the value of sec θ.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
54
The terminal side of an angle θ in standard position passes through the point (-2, -1). Calculate the value of sinθ. Round your answer to four decimal places.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
55
The terminal side of an angle θ in standard position passes through the point (-6, 1). Calculate the value of cosθ. Round your answer to four decimal places.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
56
The terminal side of an angle θ in standard position passes through the point (2, 5). Calculate the value of tanθ. Round your answer to four decimal places.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
57
The terminal side of an angle θ in standard position passes through the point (-4, 6). Calculate the value of cotθ. Round your answer to four decimal places.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
58
The terminal side of an angle θ in standard position passes through the point (7, -6). Calculate the value of cscθ. Round your answer to four decimal places.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
59
The terminal side of an angle θ in standard position passes through the point (2, 1). Calculate the value of secθ. Round your answer to four decimal places.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
60
Calculate cot if is in standard position and has a measure of 225°.
A) 0
B) -1
C) 1
D)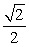
A) 0
B) -1
C) 1
D)
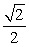

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
61
Calculate cscθ if θ is in standard position and has a measure of 1890°.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
62
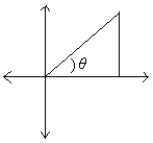
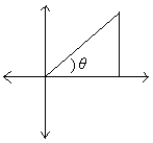
A right triangle is drawn in QI with one leg on the x-axis and its hypotenuse on the terminal side of
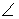
drawn in standard position. If tan =
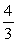
, then what is sin ?
A)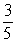
B)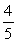
C)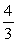
D)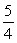
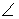
drawn in standard position. If tan =
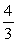
, then what is sin ?

A)
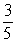
B)
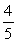
C)
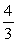
D)
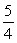

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
63
A right triangle is drawn in QI with one leg on the x-axis and its hypotenuse on the terminal side of
drawn in standard position. If tan =
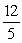
, then what is cos ?
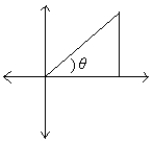
A)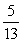
B)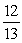
C)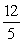
D)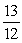
drawn in standard position. If tan =
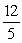
, then what is cos ?

A)
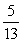
B)
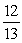
C)
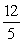
D)
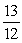

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
64
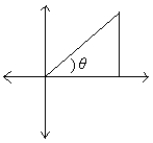
A right triangle is drawn in QI with one leg on the x-axis and its hypotenuse on the terminal side of
drawn in standard position. If sin =
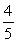
, then what is tan ?
A)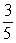
B)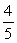
C)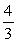
D)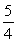
drawn in standard position. If sin =
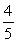
, then what is tan ?

A)
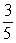
B)
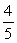
C)
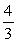
D)
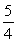

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
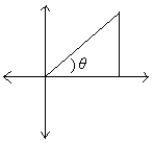
65
A right triangle is drawn in QI with one leg on the x-axis and its hypotenuse on the terminal side of
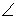
θ drawn in standard position. If tanθ =
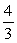
, then what is sinθ?
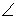
θ drawn in standard position. If tanθ =
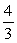
, then what is sinθ?


Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
66
A right triangle is drawn in QI with one leg on the x-axis and its hypotenuse on the terminal side of
θ drawn in standard position. If tanθ =
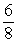
, then what is cosθ?
θ drawn in standard position. If tanθ =
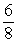
, then what is cosθ?


Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
67
A right triangle is drawn in QI with one leg on the x-axis and its hypotenuse on the terminal side of
θ drawn in standard position. If sin θ =
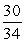
, then what is tanθ?
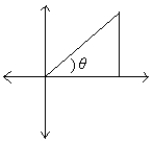
θ drawn in standard position. If sin θ =
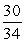
, then what is tanθ?


Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
68
Indicate the quadrant in which the terminal side of must lie in order for the following to be true.
Tan is positive and cos is negative.
A) Q1
B) QII
C) QIII
D) QIV
Tan is positive and cos is negative.
A) Q1
B) QII
C) QIII
D) QIV

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
69
Indicate the quadrant in which the terminal side of must lie in order for the following to be true:
Cos is positive and tan is negative.
A) Q1
B) QII
C) QIII
D) QIV
Cos is positive and tan is negative.
A) Q1
B) QII
C) QIII
D) QIV

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
70
Indicate the quadrant in which the terminal side of θ must lie in order for the following to be true:
sinθ is positive and tanθ is negative.
sinθ is positive and tanθ is negative.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
71
Indicate the quadrant in which the terminal side of θ must lie in order for the following to be true:
tanθ is positive and cosθ is negative.
tanθ is positive and cosθ is negative.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
72
If tan =
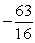
, and the terminal side of lies in quadrant II, find sin .
A)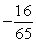
B)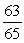
C)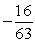
D)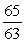
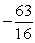
, and the terminal side of lies in quadrant II, find sin .
A)
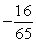
B)
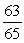
C)
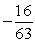
D)
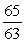

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
73
If tan =
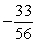
, and the terminal side of lies in quadrant II, find cos .
A)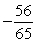
B)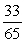
C)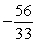
D)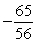
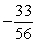
, and the terminal side of lies in quadrant II, find cos .
A)
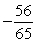
B)
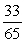
C)
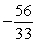
D)
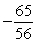

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
74
If cos =
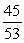
, and the terminal side of lies in quadrant I, find sin .
A)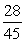
B)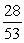
C)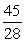
D)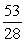
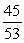
, and the terminal side of lies in quadrant I, find sin .
A)
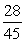
B)
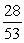
C)
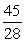
D)
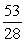

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
75
If cot =
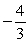
, and the terminal side of lies in quadrant II, find sec .
A)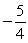
B)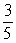
C)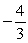
D)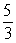
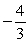
, and the terminal side of lies in quadrant II, find sec .
A)
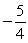
B)
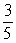
C)
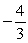
D)
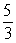

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
76
If sec =
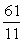
, and the terminal side of lies in quadrant I, find sin .
A)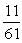
B)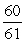
C)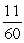
D)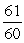
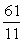
, and the terminal side of lies in quadrant I, find sin .
A)
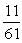
B)
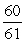
C)
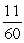
D)
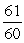

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
77
If tan =
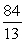
, and the terminal side of lies in quadrant III, find csc .
A)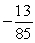
B)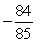
C)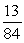
D)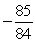
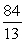
, and the terminal side of lies in quadrant III, find csc .
A)
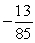
B)
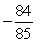
C)
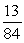
D)
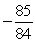

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
78
Indicate the quadrant in which the terminal side of θ must lie in order for the following to be true.
tan θ is positive and sin θ is negative.
tan θ is positive and sin θ is negative.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
79
If sinθ =
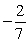
, and the terminal side of θ lies in quadrant IV, find cosθ.
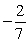
, and the terminal side of θ lies in quadrant IV, find cosθ.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck
80
If cos θ =
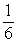
, and the terminal side of θ lies in quadrant I, find sin θ.
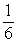
, and the terminal side of θ lies in quadrant I, find sin θ.

Unlock Deck
Unlock for access to all 261 flashcards in this deck.
Unlock Deck
k this deck


