Deck 3: The Laws of Physics Are Frame-Independent Relativity
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/124
Play
Full screen (f)
Deck 3: The Laws of Physics Are Frame-Independent Relativity
1
Which of the following are (at least nearly) inertial reference frames and which are not? (Respond T if the
frame is inertial, F if it is non inertial, and C if it is inertial for everyday purposes. The classification could be
debatable, creating an opportunity to discuss the issues involved.)
-(a) A non rotating frame floating in deep space
frame is inertial, F if it is non inertial, and C if it is inertial for everyday purposes. The classification could be
debatable, creating an opportunity to discuss the issues involved.)
-(a) A non rotating frame floating in deep space
T
2
Which of the following are (at least nearly) inertial reference frames and which are not? (Respond T if the
frame is inertial, F if it is non inertial, and C if it is inertial for everyday purposes. The classification could be
debatable, creating an opportunity to discuss the issues involved.)
-(b) A frame floating in deep space that rotates at 1 rev/h
frame is inertial, F if it is non inertial, and C if it is inertial for everyday purposes. The classification could be
debatable, creating an opportunity to discuss the issues involved.)
-(b) A frame floating in deep space that rotates at 1 rev/h
C
3
Which of the following are (at least nearly) inertial reference frames and which are not? (Respond T if the
frame is inertial, F if it is non inertial, and C if it is inertial for everyday purposes. The classification could be
debatable, creating an opportunity to discuss the issues involved.)
-(c) A non rotating frame attached to the sun
frame is inertial, F if it is non inertial, and C if it is inertial for everyday purposes. The classification could be
debatable, creating an opportunity to discuss the issues involved.)
-(c) A non rotating frame attached to the sun
C
4
Which of the following are (at least nearly) inertial reference frames and which are not? (Respond T if the
frame is inertial, F if it is non inertial, and C if it is inertial for everyday purposes. The classification could be
debatable, creating an opportunity to discuss the issues involved.)
-(d) A frame attached to the surface of the earth
frame is inertial, F if it is non inertial, and C if it is inertial for everyday purposes. The classification could be
debatable, creating an opportunity to discuss the issues involved.)
-(d) A frame attached to the surface of the earth

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following are (at least nearly) inertial reference frames and which are not? (Respond T if the
frame is inertial, F if it is non inertial, and C if it is inertial for everyday purposes. The classification could be
debatable, creating an opportunity to discuss the issues involved.)
-(e) A frame attached to a car moving at a constant velocity
frame is inertial, F if it is non inertial, and C if it is inertial for everyday purposes. The classification could be
debatable, creating an opportunity to discuss the issues involved.)
-(e) A frame attached to a car moving at a constant velocity

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
6
Which of the following are (at least nearly) inertial reference frames and which are not? (Respond T if the
frame is inertial, F if it is non inertial, and C if it is inertial for everyday purposes. The classification could be
debatable, creating an opportunity to discuss the issues involved.)
-(f) A frame attached to a roller-coaster car
frame is inertial, F if it is non inertial, and C if it is inertial for everyday purposes. The classification could be
debatable, creating an opportunity to discuss the issues involved.)
-(f) A frame attached to a roller-coaster car

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following physical occurrences fit the physical definition of an event?
A) The collision of two point particles
B) A point particle passing a given point in space
C) A firecracker explosion
D) A party at your dorm
E) A hurricane
F) A, B, and C
G) Any of the above could be an event, depending on the reference frame's scale and/or how precise the measurements need to be.
A) The collision of two point particles
B) A point particle passing a given point in space
C) A firecracker explosion
D) A party at your dorm
E) A hurricane
F) A, B, and C
G) Any of the above could be an event, depending on the reference frame's scale and/or how precise the measurements need to be.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
8
Since the laws of physics are the same in every inertial reference frame, there is no meaningful physical distinction between an inertial frame at rest and one moving at a constant velocity.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
9
Since the laws of physics are the same in every reference frame, an object must have the same kinetic energy in all inertial reference frames.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
10
Since the laws of physics are the same in every inertial reference frame, an interaction between objects must be observed to conserve energy in every inertial reference frame.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
11
Since the laws of physics are the same in every inertial reference frame, if you perform identical experiments in two different inertial frames, you should get exactly the same results.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
12
Imagine two boats. One travels eastward relative to the earth and the other eastward relative to the earth. We set up a reference frame on each boat with the axis pointing eastward, and choose the first boat (arbitrarily) to be the Home Frame. The second boat is thus the Other Frame. What is the sign of , according to the convention established in this chapter?
A) Positive
B) Negative
C) We are free to choose either sign.
A) Positive
B) Negative
C) We are free to choose either sign.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
13
You are in a spaceship traveling away from earth. You and Mission Control on earth agree that the direction is the direction in which your ship is traveling relative to the earth. If you choose your own frame to be the Home Frame (so that the earth is the Other Frame), what is the sign of , according to the convention established in this chapter?
A) Positive
B) Negative
C) We are free to choose to have either sign.
A) Positive
B) Negative
C) We are free to choose to have either sign.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
14
Suppose you observe a collision of an isolated system of two particles. A friend observes the same collision in a reference frame moving in the direction with respect to yours. According to the Galilean transformation equations, on which aspects of the collision will you agree with your friend? (Answer T or F.)
-(a) On the value of the system's total -momentum
-(a) On the value of the system's total -momentum

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
15
Suppose you observe a collision of an isolated system of two particles. A friend observes the same collision in a reference frame moving in the direction with respect to yours. According to the Galilean transformation equations, on which aspects of the collision will you agree with your friend? (Answer T or F.)
-(b) On the value of the system's total -momentum
-(b) On the value of the system's total -momentum

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
16
Suppose you observe a collision of an isolated system of two particles. A friend observes the same collision in a reference frame moving in the direction with respect to yours. According to the Galilean transformation equations, on which aspects of the collision will you agree with your friend? (Answer T or F.)
-(c) On the value of the system's total -momentum
-(c) On the value of the system's total -momentum

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
17
Suppose you observe a collision of an isolated system of two particles. A friend observes the same collision in a reference frame moving in the direction with respect to yours. According to the Galilean transformation equations, on which aspects of the collision will you agree with your friend? (Answer T or F.)
-(d) On the force that one particle exerts on the other
-(d) On the force that one particle exerts on the other

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
18
Suppose you observe a collision of an isolated system of two particles. A friend observes the same collision in a reference frame moving in the direction with respect to yours. According to the Galilean transformation equations, on which aspects of the collision will you agree with your friend? (Answer T or F.)
-(e) That the system's total momentum is conserved
-(e) That the system's total momentum is conserved

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
19
Suppose you are in a train traveling at one-half of the speed of light relative to the earth. Assuming that photons emitted by the train's headlight travel at the speed of light relative to you, they would (according to the Galilean velocity transformation) travel at 1.5 times the speed of light relative to the earth.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
20
Suppose you are in a spaceship traveling at twice the speed of light relative to the earth. Assuming that the Galilean transformation equations are true and the earth is approximately at rest relative to the ether, light from the ship's taillight will never reach the ship's bridge at its front end.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
21
Suppose the Galilean transformation equations are true and your spaceship is moving at twice the speed of light relative to the ether. What odd things will you observe in your spaceship? Select all that apply. (If you are using the back of the book to communicate your answers, you can point to multiple letters with several fingers.)
A) You won't be able to see anything behind you.
B) You won't be able to see anything in front of you.
C) The beam from a laser pointer facing forward and a bit to your right will get curved toward the ship's stern.
D) Light from stars in front of you will become infinitely blue-shifted.
E) Stars a bit to the right or left of the forward direction will have their apparent positions shifted dramatically toward the ship's stern.
F) You will see none of these effects.
G) You will see all of these effects.
A) You won't be able to see anything behind you.
B) You won't be able to see anything in front of you.
C) The beam from a laser pointer facing forward and a bit to your right will get curved toward the ship's stern.
D) Light from stars in front of you will become infinitely blue-shifted.
E) Stars a bit to the right or left of the forward direction will have their apparent positions shifted dramatically toward the ship's stern.
F) You will see none of these effects.
G) You will see all of these effects.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
22
Imagine that in the distant future you (on earth) are watching a transmission from Pluto, which at the time is 5.0 light-hours from earth. You notice that a clock on the wall behind the person speaking in the video reads 12:10 p.m. You note that your watch reads exactly the same time. Is the station clock synchronized with your watch?
A) Yes, it is.
B) No, it isn't.
C) The problem doesn't give enough information to tell.
A) Yes, it is.
B) No, it isn't.
C) The problem doesn't give enough information to tell.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
23
Suppose you receive a message from a starbase that is 13.0 light-years from earth. The message is dated July 15, 2127. What year does your calendar indicate at the time of reception if your calendar and the station's calendar are correctly synchronized?
A) 2127
B) 2114
C) 2140
D) Other (specify)
A) 2127
B) 2114
C) 2140
D) Other (specify)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
24
The speed of a typical car on the freeway expressed in SR units is most nearly
A)
B)
C)
D)
E)
F) Other (specify)
G) None of these answers is right: we must state units!
A)
B)
C)
D)
E)
F) Other (specify)
G) None of these answers is right: we must state units!

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
25
Suppose you are sitting at the origin of an inertial reference frame. You see (that is, you receive the light from) an event occurring near a clock at at a time . When do you observe that event to occur?
A)
B)
C)
D) , of course
E)
F) Some other time (specify)
A)
B)
C)
D) , of course
E)
F) Some other time (specify)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
26
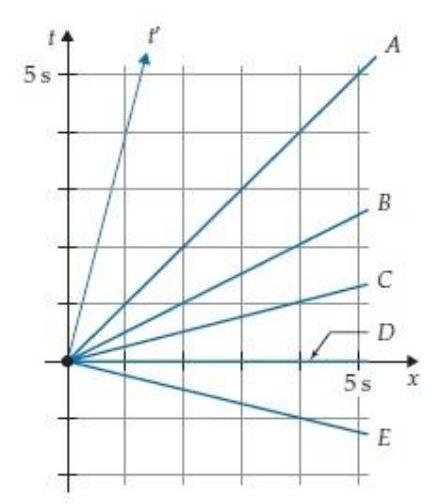
The space time diagram in figure R2.12 shows the world lines of various objects. Which object has the largest speed at time ?
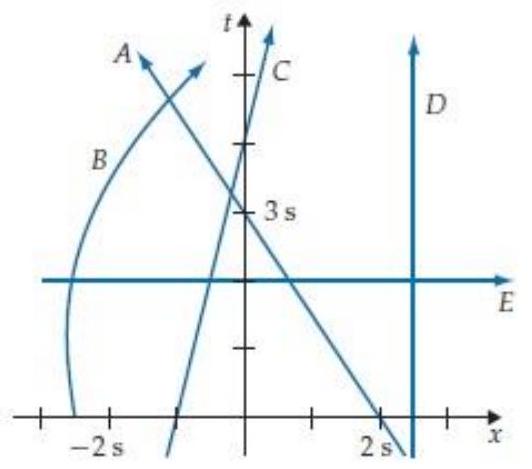
A) A
B) B
C) C
D) D
E) E

A) A
B) B
C) C
D) D
E) E

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
27
The space time diagram in figure R2.12 shows the world lines of various objects. Which object has the largest speed at time ?
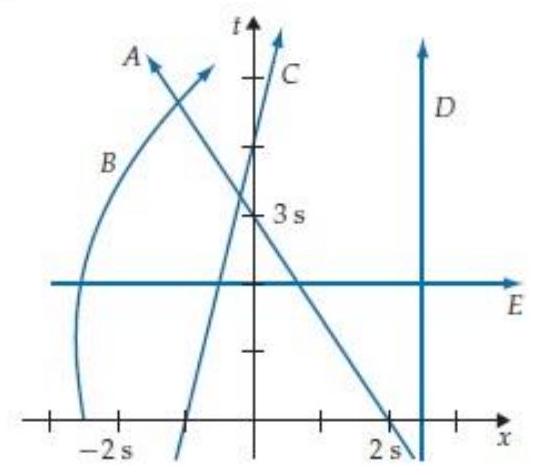
A) A
B) B
C) C
D) D
E) E

A) A
B) B
C) C
D) D
E) E

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
28
The space time diagram in figure R2.12 shows the world lines of various objects. Which world line cannot possibly be correct? (Explain why.)
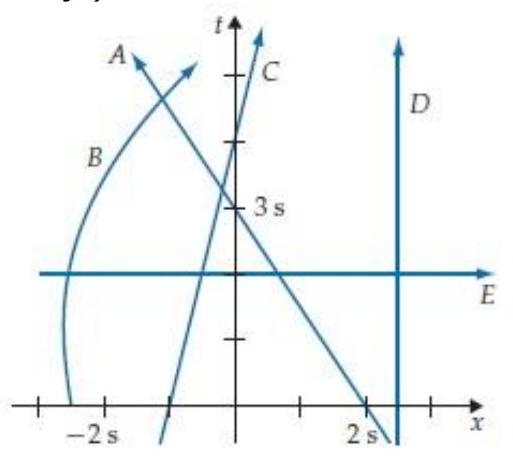
A) A
B) B
C) C
D) D
E) E

A) A
B) B
C) C
D) D
E) E

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
29
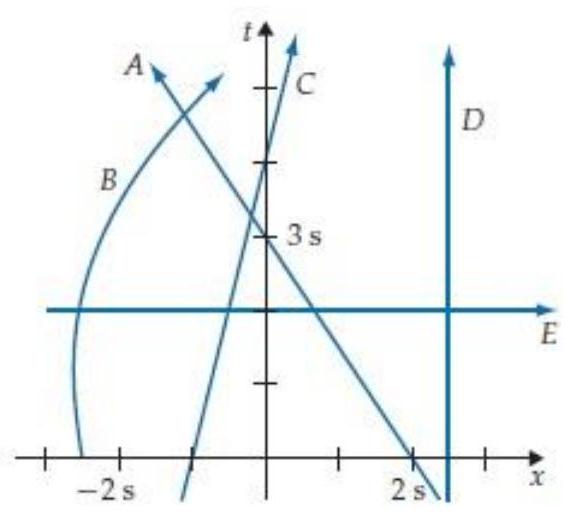
In figure R2.12, the object whose world line is labelled is moving along the axis.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
30
A light flash leaves a master clock at at time , is reflected from an object a certain distance in the direction from the origin, and then returns to the origin at . From this information, we can infer that the spacetime coordinates of the reflection event are
A)
B)
C)
D)
E)
F) Other (specify)
A)
B)
C)
D)
E)
F) Other (specify)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
31
Coordinate time would be frame-independent if the Newtonian concept of time were valid.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
32
Consider a Home Frame and an Other Frame that moves in the direction with respect to the Home Frame.
-(a) Observers in the Home Frame will conclude that the clocks in an Other Frame will be out of synchronization, even if the observers in the Other Frame have carefully synchronized clocks using the Einstein prescription.
-(a) Observers in the Home Frame will conclude that the clocks in an Other Frame will be out of synchronization, even if the observers in the Other Frame have carefully synchronized clocks using the Einstein prescription.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
33
Consider a Home Frame and an Other Frame that moves in the direction with respect to the Home Frame.
-(b) Specifically, Home Frame observers will see that for events farther and farther up the common axis, the times registered by Other Frame clocks at the events
A) Become further and further ahead.
B) Become further and further behind.
C) Remain the same.
D) Have no clear relationship to the values that Home Frame clocks register for the same events.
-(b) Specifically, Home Frame observers will see that for events farther and farther up the common axis, the times registered by Other Frame clocks at the events
A) Become further and further ahead.
B) Become further and further behind.
C) Remain the same.
D) Have no clear relationship to the values that Home Frame clocks register for the same events.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
34
In the geometric analogy, the coordinate time difference between two events in space time corresponds to
A) The north-south separation between points on a plane.
B) The distance between points on a plane.
C) A certain path length between points on a plane.
D) The separation between the events in space time.
E) Something else (specify).
A) The north-south separation between points on a plane.
B) The distance between points on a plane.
C) A certain path length between points on a plane.
D) The separation between the events in space time.
E) Something else (specify).

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
35
A person riding a merry-go-round passes very close to a person standing on the ground once (event ) and then again (event ). Assume the ground is an inertial frame and that the rider moves at a constant speed.
-(a) Which person's watch measures a proper time between events and ?
A) The rider in the merry-go-round
B) The person standing on the ground
C) Both
D) Neither
-(a) Which person's watch measures a proper time between events and ?
A) The rider in the merry-go-round
B) The person standing on the ground
C) Both
D) Neither

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
36
A person riding a merry-go-round passes very close to a person standing on the ground once (event ) and then again (event ). Assume the ground is an inertial frame and that the rider moves at a constant speed.
-(b) Which person's watch measures the spacetime interval between those events?
A) The rider in the merry-go-round
B)The person standing on the ground
C) Both
D) Neither
-(b) Which person's watch measures the spacetime interval between those events?
A) The rider in the merry-go-round
B)The person standing on the ground
C) Both
D) Neither

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
37
A person riding a merry-go-round passes very close to a person standing on the ground once (event ) and then again (event ). Assume the ground is an inertial frame and that the rider moves at a constant speed.
-(c) Which person's watch (if any) measures the coordinate time between those events in some inertial frame?
A) The rider in the merry-go-round
B)The person standing on the ground
C) Both
D) Neither
-(c) Which person's watch (if any) measures the coordinate time between those events in some inertial frame?
A) The rider in the merry-go-round
B)The person standing on the ground
C) Both
D) Neither

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
38
A spaceship departs from the solar system (event ) and travels at a constant velocity to a distant star. It then returns at a constant velocity, finally returning to the solar system (event ). A clock on the spaceship registers which of the following kinds of time between these events?
A) Proper time
B) Coordinate time
C) Space time interval
D) Proper time and space time interval
E) Coordinate time and space time interval
F) All three
A) Proper time
B) Coordinate time
C) Space time interval
D) Proper time and space time interval
E) Coordinate time and space time interval
F) All three

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
39
Alice bungee-jumps from a bridge above a deep gorge. Bob watches from the bridge. Let event be Alice's departure from Bob's location on the bridge, and event be her return to Bob's location on the bridge. Carol observes these events from a a train passing over the bridge, and uses synchronized clocks on the train to measure the time between Alice's departure and return.
-(a) Which person's watch or clocks register(s) a proper time between events and ?
A) Alice
B) Bob
C) Carol
D) Alice and Bob
E) Bob and Carol
F) Alice and Carol
G) All three observers
-(a) Which person's watch or clocks register(s) a proper time between events and ?
A) Alice
B) Bob
C) Carol
D) Alice and Bob
E) Bob and Carol
F) Alice and Carol
G) All three observers

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
40
Alice bungee-jumps from a bridge above a deep gorge. Bob watches from the bridge. Let event be Alice's departure from Bob's location on the bridge, and event be her return to Bob's location on the bridge. Carol observes these events from a a train passing over the bridge, and uses synchronized clocks on the train to measure the time between Alice's departure and return.
-(b) Which person's watch or clocks register(s) the space time interval between those events?
A) Alice
B) Bob
C) Carol
D) Alice and Bob
E) Bob and Carol
F) Alice and Carol
G) All three observers
-(b) Which person's watch or clocks register(s) the space time interval between those events?
A) Alice
B) Bob
C) Carol
D) Alice and Bob
E) Bob and Carol
F) Alice and Carol
G) All three observers

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
41
Alice bungee-jumps from a bridge above a deep gorge. Bob watches from the bridge. Let event be Alice's departure from Bob's location on the bridge, and event be her return to Bob's location on the bridge. Carol observes these events from a a train passing over the bridge, and uses synchronized clocks on the train to measure the time between Alice's departure and return.
-(c) Which person's watch or clocks register(s) a coordinate time between those events in some inertial frame?
A) Alice
B) Bob
C) Carol
D) Alice and Bob
E) Bob and Carol
F) Alice and Carol
G) All three observers
-(c) Which person's watch or clocks register(s) a coordinate time between those events in some inertial frame?
A) Alice
B) Bob
C) Carol
D) Alice and Bob
E) Bob and Carol
F) Alice and Carol
G) All three observers

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
42
The space time interval between two events can never be larger than the coordinate time between those events as measured in any inertial reference frame.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
43
Two events occur apart in time and apart in space. A clock traveling at a speed of be present at both these events. What time interval will such a clock measure between the events?
A)
B)
C)
D)
E)
F) Other (specify)
A)
B)
C)
D)
E)
F) Other (specify)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
44
Consider the events , and shown in the space time diagram below.
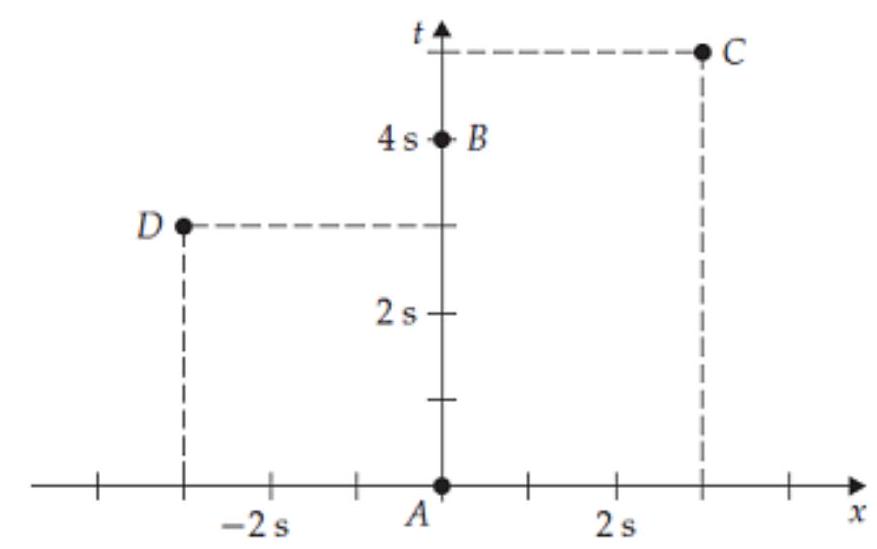
-(a) What is the space time interval between events A and B?
A)
B)
C)
D)
E)
F) Other (specify)

-(a) What is the space time interval between events A and B?
A)
B)
C)
D)
E)
F) Other (specify)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
45
Consider the events , and shown in the space time diagram below.

-(b) Between A and C?
A)
B)
C)
D)
E)
F) Other (specify)

-(b) Between A and C?
A)
B)
C)
D)
E)
F) Other (specify)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
46
Consider the events , and shown in the space time diagram below.

-(c) Between and ?
A)
B)
C)
D)
E)
F) Other (specify)

-(c) Between and ?
A)
B)
C)
D)
E)
F) Other (specify)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
47
Consider the space time diagram below. Let the space time interval between events and be , and let the space time interval between events and be Which of these two space time intervals is larger? (Assume that the and coordinates of all these events are zero.)
A)
B)
C)
D) There is no way to tell from this diagram.

A)
B)
C)
D) There is no way to tell from this diagram.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
48
An inertial clock present at two events always measures a shorter time than a pair of synchronized clocks in any inertial reference frame would register between the same two events (as long as the events don't occur at the same place in that frame).

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
49
Consider a train moving at a speed of 0.6 relative to the ground. A light in one of its windows blinks repeatedly. An observer on the ground will necessarily see (not observe) those blinks to be separated by a larger time interval than a person on the train would.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
50
Suppose we carefully synchronize two identical atomic clocks initially standing next to each other (call them and ). We put clock on a jet plane, which then flies around the world at an essentially constant speed of , returning later. We then again compare the two clocks. Assume the earth's surface defines an inertial reference frame, and ignore the possible effects of gravity.
-(a) Which clock measures the space time interval between the synchronization and comparison events?
A) Clock
B) Clock
C) Both
D) Neither
-(a) Which clock measures the space time interval between the synchronization and comparison events?
A) Clock
B) Clock
C) Both
D) Neither

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
51
Suppose we carefully synchronize two identical atomic clocks initially standing next to each other (call them and ). We put clock on a jet plane, which then flies around the world at an essentially constant speed of , returning later. We then again compare the two clocks. Assume the earth's surface defines an inertial reference frame, and ignore the possible effects of gravity.
-(b) Which clock measures a coordinate time between the synchronization and comparison events?
A) Clock
B) Clock
C) Both
D) Neither
-(b) Which clock measures a coordinate time between the synchronization and comparison events?
A) Clock
B) Clock
C) Both
D) Neither

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
52
Suppose we carefully synchronize two identical atomic clocks initially standing next to each other (call them and ). We put clock on a jet plane, which then flies around the world at an essentially constant speed of , returning later. We then again compare the two clocks. Assume the earth's surface defines an inertial reference frame, and ignore the possible effects of gravity.
-(c) Which clock measures the shorter time interval between the synchronization and comparison events (or do both measure the same time)?
A) Clock A
B) Clock
C) Both
D) Neither
-(c) Which clock measures the shorter time interval between the synchronization and comparison events (or do both measure the same time)?
A) Clock A
B) Clock
C) Both
D) Neither

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
53
In the round-the-world experiment described in problem R4T.2, what is the minimum accuracy over the experiment's duration that the clocks must have to clearly display the relativistic effect?
A) Both clocks must be accurate to the nearest .
B) Both clocks must be accurate to the nearest .
C) Both clocks must be accurate to the nearest .
D) Both clocks must be accurate to the nearest 10 ps.
A) Both clocks must be accurate to the nearest .
B) Both clocks must be accurate to the nearest .
C) Both clocks must be accurate to the nearest .
D) Both clocks must be accurate to the nearest 10 ps.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
54
Jennifer bungee-jumps from a bridge (event A). Jennifer's bungee cord is perfectly elastic, so she bounces exactly back up to the bridge and lands on her feet (event B). The time between these events is measured by Jennifer's watch, a stopwatch held by Jennifer's friend, Rob, who is standing on the bridge, and by two passengers (one present at event and one present at event ) who are riding on a train traveling at a constant velocity across the bridge at the time (the passengers have synchronized watches and compare readings later). Assuming the earth's frame is inertial, who measures
-(a) the longest time interval between these events?
A) Jennifer
B) Rob
C) The train passengers
-(a) the longest time interval between these events?
A) Jennifer
B) Rob
C) The train passengers

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
55
Jennifer bungee-jumps from a bridge (event A). Jennifer's bungee cord is perfectly elastic, so she bounces exactly back up to the bridge and lands on her feet (event B). The time between these events is measured by Jennifer's watch, a stopwatch held by Jennifer's friend, Rob, who is standing on the bridge, and by two passengers (one present at event and one present at event ) who are riding on a train traveling at a constant velocity across the bridge at the time (the passengers have synchronized watches and compare readings later). Assuming the earth's frame is inertial, who measures
-(b) the shortest time interval between these events?
A) Jennifer
B) Rob
C) The train passengers
-(b) the shortest time interval between these events?
A) Jennifer
B) Rob
C) The train passengers

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
56
Jennifer bungee-jumps from a bridge (event A). Jennifer's bungee cord is perfectly elastic, so she bounces exactly back up to the bridge and lands on her feet (event B). The time between these events is measured by Jennifer's watch, a stopwatch held by Jennifer's friend, Rob, who is standing on the bridge, and by two passengers (one present at event and one present at event ) who are riding on a train traveling at a constant velocity across the bridge at the time (the passengers have synchronized watches and compare readings later). Assuming the earth's frame is inertial, who measures
-(c) the space time interval between the events?
A) Jennifer
B) Rob
C) The train passengers
-(c) the space time interval between the events?
A) Jennifer
B) Rob
C) The train passengers

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
57
In the situation described in problem R4T.4, the train passengers are moving, but Rob is at rest. Therefore, the train passengers measure less time between the events than Rob does.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
58
Suppose we synchronize two atomic clocks at a point at south latitude, and then move one clock directly north to the earth's equator and the other directly south to the south pole, where they remain for some years in climate-controlled enclosures that keep them at the same temperature and humidity. We then reunite the clocks at the origin point and compare them again. Which (if either) has registered a shorter time between the synchronization and comparison events?
A) The clock at the equator}
B) The clock at the south pole
C) Both clocks read the same time.
A) The clock at the equator}
B) The clock at the south pole
C) Both clocks read the same time.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
59
GPS satellites go around the earth in orbits that have a common radius of and a period of . Roughly how much less time would an atomic clock on a GPS satellite register between two events separated by exactly 24 than clocks in the reference frame of the earth (ignoring gravitational effects on the satellite's clock rate)?
A) About
B) About
C) About
D) About 10 us
E) About 1 rs
F) About 10 ns
A) About
B) About
C) About
D) About 10 us
E) About 1 rs
F) About 10 ns

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
60
The coordinate time between two given events is shortest in the inertial frame where their spatial separation is the smallest.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
61
The Other Frame is moving in the direction with -velocity with respect to the Home Frame. The two-observer space time diagram in figure R5.9 shows the diagram and axes of the Home Frame and the diagram axis of the Other Frame. Which of the choices in that Figure best corresponds to the diagram axis?
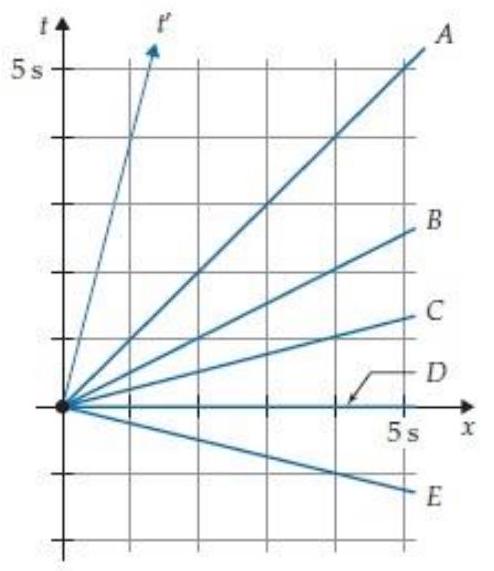


Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
62
The Other Frame is moving in the direction with -velocity with respect to the Home Frame. The two-observer space time diagram in figure R5.9 shows the diagram and axes of the Home Frame and the diagram axis of the Other Frame. Which of the choices in that figure would best correspond to the diagram axis if the Newtonian concept of time were true?
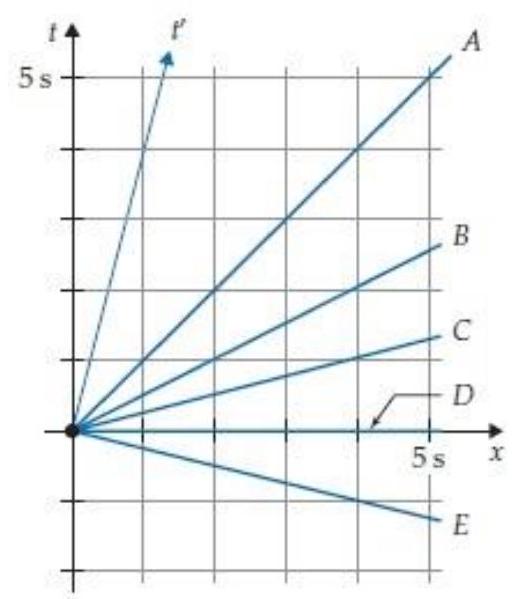


Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
63
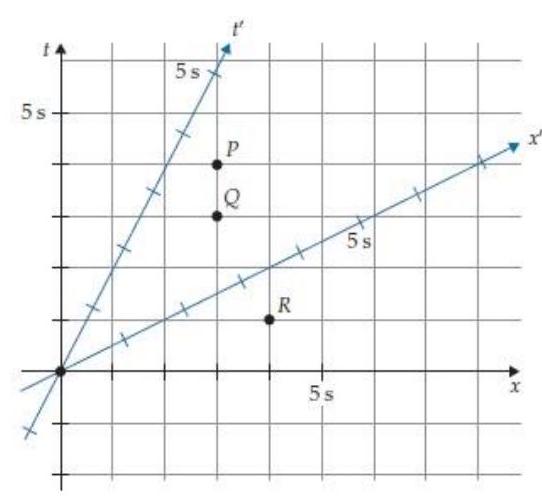
Suppose the marks on the Home Frame axis in figure R5.9 are apart. What should be the vertical separation of the corresponding marks on the ' axis?
A)
B)
C)
D)
E)
F) Other

A)
B)
C)
D)
E)
F) Other

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
64
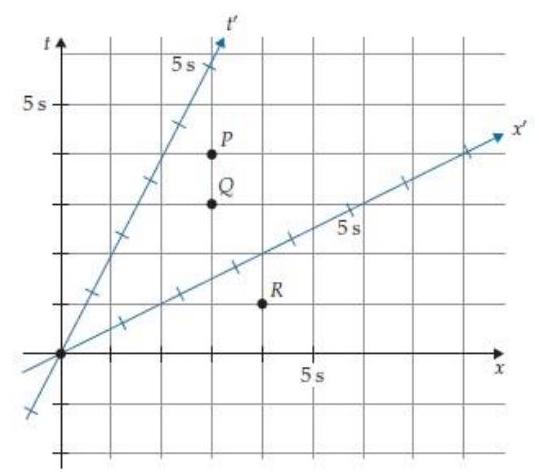
Figure R5.10 shows a two-observer space time diagram for an Other Frame that moves at a speed of 0.5 relative to the Home Frame. What are the coordinates of event in the Other Frame?
A)
B)
C)
D)
E) Other (specify)

A)
B)
C)
D)
E) Other (specify)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
65
Figure R5.10 shows a two-observer space time diagram for an Other Frame that moves at a speed of 0.5 relative to the Home Frame. What are the coordinates of event in the Other Frame?
A)
B)
C)
D)
E) Other (specify)

A)
B)
C)
D)
E) Other (specify)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
66
Figure R5.10 shows a two-observer space time diagram for an Other Frame that moves at a speed of 0.5 relative to the Home Frame. What are the coordinates of event in the Other Frame?
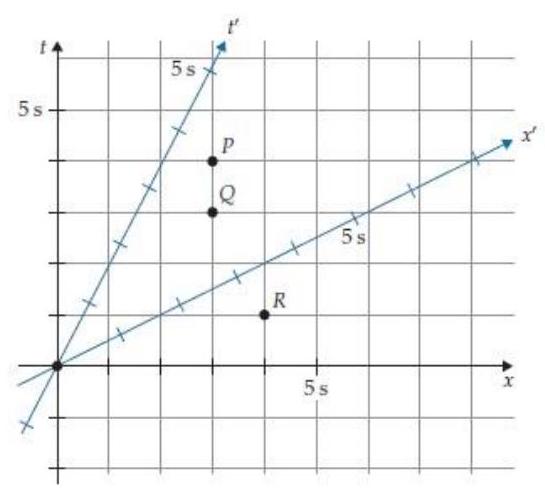
Figure R5.10
A)
B)
C)
D)
E) Other (specify)

Figure R5.10
A)
B)
C)
D)
E) Other (specify)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
67
Consider two blinking warning lights apart along a railroad track. These lights flash simultaneously in the ground frame. Let be the event of the west light blinking, and let be the event of the east light blinking. train moves eastward along the track at a relativistic speed . Suppose an observer in the train passes the west light just as event happens. By carefully measuring when the light from event arrives and calculating the distance between the two lights (by observing how long it takes to travel between the lights at the known speed ), the observer is able to infer when event actually happened in the train frame. The observer concludes that
A) Event happened before event in the train frame.
B) Events and were simultaneous in the train frame.
C) Event happened before event in the train frame.
D) One cannot determine unambiguously which event occurs first in the train frame.
A) Event happened before event in the train frame.
B) Events and were simultaneous in the train frame.
C) Event happened before event in the train frame.
D) One cannot determine unambiguously which event occurs first in the train frame.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
68
A bullet train moving in the direction with -velocity relative to the ground has lights on the roof of the head and tail cars that blink simultaneously in the train frame. The head car's light happens to be passing by an observer on the ground just as it blinks. The observer sees the light from the tail car at a different time, but after correcting for the light travel time from the tail car, the observer concludes that in the ground frame
A) The tail car's light blinked before the head car's light.}
B) The head car's light blinked before the tail car's light.
C) Both lights blinked simultaneously.
D) One cannot determine unambiguously which event occurs first in the ground frame.
A) The tail car's light blinked before the head car's light.}
B) The head car's light blinked before the tail car's light.
C) Both lights blinked simultaneously.
D) One cannot determine unambiguously which event occurs first in the ground frame.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
69
Two lights are 1000 ns apart along a stretch of railway track. In the ground frame, the west light flashes before the east light flashes. Could these flashes be simultaneous in the frame of a train moving along the track at a certain speed (that is less than the speed of light)?
A) Yes, if the train is moving east at the correct speed.
B) Yes, if the train is moving west at the correct speed.
C) Yes, if the train observer happens to be at the right distances from the lights when receiving their flashes.
D) No, the flashes cannot be simultaneous in any frame.
A) Yes, if the train is moving east at the correct speed.
B) Yes, if the train is moving west at the correct speed.
C) Yes, if the train observer happens to be at the right distances from the lights when receiving their flashes.
D) No, the flashes cannot be simultaneous in any frame.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
70
According to our conventional frame names, the Home Frame is the frame at rest.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
71
A moving object's length in a given frame is defined to be the distance between two events that occur at opposite ends of the object and that are simultaneous in that frame. Why is it crucial that the events we use to define a moving object's length be simultaneous?
A) This is purely conventional: there is no other reason.
B) This choice makes it easier to use the Lorentz transformation equations to find the length.
C) If the events are not constrained to be simultaneous, then the length is poorly defined: its value would depend on the time interval between the events.
D) If the events are simultaneous, then the length will be a frame-independent quantity.
E) Other (specify)
A) This is purely conventional: there is no other reason.
B) This choice makes it easier to use the Lorentz transformation equations to find the length.
C) If the events are not constrained to be simultaneous, then the length is poorly defined: its value would depend on the time interval between the events.
D) If the events are simultaneous, then the length will be a frame-independent quantity.
E) Other (specify)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
72
Since an object's ends do not move in its rest frame, the events used to mark out an object's length in that frame do not have to be simultaneous: the distance between them is the object's rest length whether they are simultaneous or not.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
73
An object of rest length moving at one-half the speed of light will have a length equal to:
A)
B)
C)
D)
E)
F) Other (specify)
A)
B)
C)
D)
E)
F) Other (specify)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
74
An object is at rest in the Home Frame. Imagine an Other Frame moving at a speed of with respect to the Home Frame. The object's length in the Other Frame is measured to be . What is its length as observed in the Home Frame?
A)
B)
C)
D)
E) 25 ns
F) Other (specify)
A)
B)
C)
D)
E) 25 ns
F) Other (specify)

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
75
An object's length would be negative in a frame where it travels faster than the speed of light.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
76
Suppose an object is in a frame where it is moving at speed and its length is at that speed. If we double the speed , then the object's length is compressed by a factor of two .

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
77
The most important reason an object is observed to be shorter in a frame where it is moving than in a frame where it is at rest is that
A) The force of motion strongly compresses an object that is moving at relativistic speeds.
B) "Simultaneity" is not a frame-independent concept.
C) The measuring sticks used by the moving observer are Lorentz-contracted.
D) The clocks used by the moving observer run slower.
A) The force of motion strongly compresses an object that is moving at relativistic speeds.
B) "Simultaneity" is not a frame-independent concept.
C) The measuring sticks used by the moving observer are Lorentz-contracted.
D) The clocks used by the moving observer run slower.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
78
In the pole and barn problem, the barn never actually encloses the pole in the ground frame.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
79
We can define a moving object's length to be its speed times the time it takes to pass a given point.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck
80
Consider the events shown in the figure below:
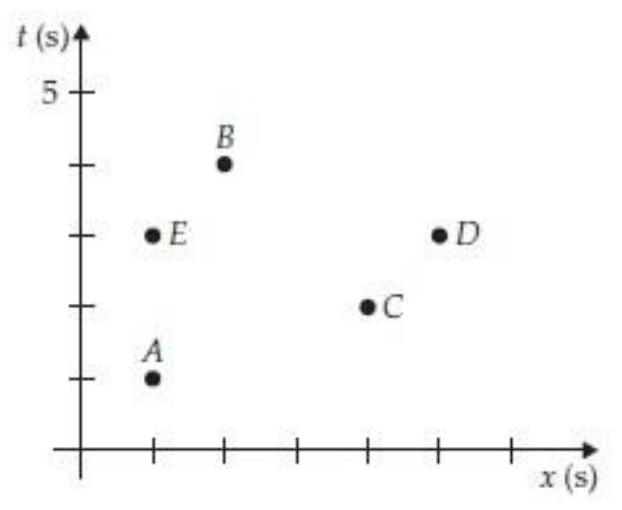
For each of the ten event pairs in this space time diagram, classify the space time interval between them.
A. The interval is time like.
B. The interval is light like.
C. The interval is space like.

For each of the ten event pairs in this space time diagram, classify the space time interval between them.
A. The interval is time like.
B. The interval is light like.
C. The interval is space like.

Unlock Deck
Unlock for access to all 124 flashcards in this deck.
Unlock Deck
k this deck


