Deck 29: Applied Applications of the Derivative

Question 1

The current in a $7.50-\mathrm{H}$ inductor is given by $i=1.8 t^{2}-6.2 t$ . Find the voltage across the inductor at $2.75 \mathrm{~s}$ .

Answer 1

$27.75 \mathrm{~V}$

Question 2

The charge through a resistor is given by $q=2.93 t^{3}-3.98 t$ . Write an expression for the instantaneous current through the resistor. Evaluate at $t=4.00 \mathrm{~s}$ .

Answer 2

$i=8.79 t^{2}-3.98,137 \mathrm{~A}$

Question 3

The current in a $1.00-\mathrm{H}$ inductor is given by $i=\sqrt{6.02 t^{2}+20.1} t$ . Find the voltage across the inductor at $6.00 \mathrm{~s}$ .

Answer 3

$2.51 \mathrm{~V}$

Question 4

If a voltage of $v=1.7 t^{2}-3.2 t+1.3$ is applied to a $250-\mu \mathrm{F}$ capacitor, what is the current when $0.3 \mathrm{sec}$ ?

Question 5

The charge through a resistor is given by $q=4 t^{3}-9 t^{2}$ . What is the current through the resistor at $5.0 \mathrm{~s}$ ?

Question 6

Find the voltage across a $12.5-\Omega$ resistor at $2.50 \mathrm{~s}$ if the charge through the resistor is given by $q=8 \sqrt{4 t-1}$ .

Question 7

The voltage applied to a $0.25-\mathrm{F}$ capacitor is given by $v=\frac{\left(t^{2}-2 t\right)^{3}}{5 t}$ . Find the current at $3.7 \mathrm{~s}$ .

Question 8

The temperature $T\left({ }^{\circ} \mathrm{C}\right)$ at distance $x(\mathrm{~mm})$ from the end of a certain heated bar is given by $T(x)=2.0 x^{1.5}$ $+4.0 x+7.0$ . Find the rate of change of temperature with respect to distance at the point $55 \mathrm{~mm}$ from the end.

Question 9

The air in a container is at a pressure of $27.1 \mathrm{lb} / \mathrm{in}^{3}$ when its volume is $96.0 \mathrm{in}^{3}$ . Find the rate of change of the volume with respect to pressure as the pressure increases. Use Boyles' Law, $p v=k$ .

Question 10

The temperature $T\left({ }^{\circ} \mathrm{C}\right)$ of a point $r \mathrm{~cm}$ from the center of a particular metal disc being heated up is given by $T=0.4 r^{2}+\pi r+87$ . Find the rate of change of temperature with respect to distance at a point $6.0 \mathrm{~cm}$ from the center.

Question 11

The voltage applied to a $0.250-F$ capacitor is given by $v=15.0 t^{2}-48.0 t+40.0$ . Find the current at $6.25 \mathrm{~s}$ .

Question 12

The distance $(\mathrm{m})$ that a point travels in $t$ seconds is given by $s=\sqrt{5+t^{2}}$ . Find the velocity and acceleration of the point at $2 \mathrm{~s}$ .

Question 13

A point moves according to the equation $s=3.0 t^{3}-64 t$ , where $s$ is in centimetres and $t$ is in seconds.
(a) Find the time $t$ in seconds greater than zero when the point comes to rest and the distance it traveled in this time.
(b) Find the non-zero time when the point crosses its starting point.

Question 14

A point is moving along the curve $y^{2}=3 x^{2}-12 x$ so that its $y$ -value increases at a constant rate of 3 units/s. How fast is the $x$ -value changing when the $x$ -value of the point increases to 6 ?

Question 15

A point moves along the curve that has the parametric equations $x=8 t^{3}-3 t^{2}$ and $y=6 t^{3}+25, x$ and $y$ being in metres and $t$ being in minutes. Find the magnitude and direction of the acceleration when $t=2.50$ minutes.

Question 16

Find the instantaneous velocity and acceleration at the given time for the straight-line motion described by the equation $s=12 t^{2}-t+15$ at $t=2.0 \mathrm{~s}$ , where $s$ is in centimetres.

Question 17

Find the instantaneous velocity and acceleration at the given time for the straight-line motion described by the equation: $s=(t+2)^{4}-\frac{1}{(t+2)^{2}}$ at $1.000 \mathrm{~s}$ , where $s$ is in centimetres.

Question 18

A point moves along the curve $y=2 x^{4}-10 x^{2}-x+2 \mathrm{~cm}$ .
(a) Find the direction of travel at $x=2.01 \mathrm{~cm}$ .
(b) If the speed of the point along the curve is $4.81 \mathrm{~cm} / \mathrm{s}$ , find the $x$ and $y$ components of the velocity when $x=2.01 \mathrm{~cm}$ .

Question 19

A point has horizontal and vertical displacements (in $\mathrm{cm}$ ) of $x=3 t^{3}+5 t$ and $y=13+5 t^{2}$ . Find the $x$ and $y$ components of the velocity and acceleration at $t=2.00 \mathrm{~s}$ .

Question 20

A point has horizontal and vertical displacements (in $\mathrm{cm}$ ) of $x=t^{3}-t^{2}+5 t$ and $y=24-t^{3}+t$ . Find the magnitude and direction of the resultant velocity at $t=3.50 \mathrm{~s}$ .

Question 21

The angular displacement of a rotating body is given by $\theta=47 t^{3}-75 \sqrt{t}$ in radians. Find the angular velocity and the angular acceleration at $1.50 \mathrm{~s}$ .

Question 22

Find the instantaneous acceleration of an object at $1.20 \mathrm{~s}$ given that its path follows $s=2 t^{3}+5 t-8 \mathrm{~cm}$ .

Question 23

What is the velocity at 3 seconds of an object with displacement $s=t^{3}-7 t \mathrm{~m}$ ?

Question 24

The angular displacement of a spinning shaft is given as $\theta=0.7 t^{2}-5 t+3$ , where $\theta$ is in radians and $t$ is in seconds. Find the angular velocity after one minute.

Question 25

The displacement (in $\mathrm{cm}$ ) of a point is given by $s=4 t^{3}-3 \sqrt{1+2 t}$ . Find the instantaneous velocity and acceleration at $t=1.5 \mathrm{~s}$ .

Question 26

The displacement in metres of an arrow shot straight up is giving by $s=35 t-4.9 t^{2}$ , where $t$ is in seconds. Find the maximum height reached by the arrow.

Question 27

A rocket fired at $275 \mathrm{~m} / \mathrm{s}$ at $36^{\circ}$ angle of elevation is described by $x=\left(275 \cos 36^{\circ}\right) t$ and $y=\left(275 \sin 36^{\circ}\right) t-4.9 t^{2}$ . Find the velocity (magnitude and direction) at $8 \mathrm{~s}$ .

Question 28

The angular displacement in radians is given by $\theta=8 \sqrt{t^{2}+2}$ . Find the angular velocity and angular acceleration at $0.25 \mathrm{~s}$ .

Question 29

The end of a robotic arm follows the displacement equation $s=2 t^{3}-3 t^{2}+t-3$ where $\mathrm{s}$ is in $\mathrm{mm}$ . What is the acceleration at the end of the arm after $1.5 \mathrm{~s}$ ?

Question 30

A plane moves according to $s=225 t^{2}-2.5 t^{3}$ , where $t$ is in minutes and $s$ in metres. What is the maximum speed attained by the plane?

Question 31

The angular displacement of a rotating object is given by $\theta=\frac{1}{4} t\left(t^{2}+1\right)^{3}$ in radians. Find the angular acceleration of the object at $2.400 \mathrm{~s}$ .

Question 32

A car drives towards a $111 \mathrm{~m}$ skyscraper at $7.62 \mathrm{~m} / \mathrm{s}$ . How fast is the car approaching the top of the building when the car is $68.6 \mathrm{~m}$ from the base of the building?

Question 33

A submarine passes $30 \mathrm{~m}$ beneath a boat while traveling at $8.89 \mathrm{~m} / \mathrm{s}$ on a course of $\mathrm{N} 34^{\circ} 21^{\prime} \mathrm{W}$ . The boat continues on a heading of $\mathrm{N} 55^{\circ} 39^{\prime} \mathrm{E}$ at a speed of $13.3 \mathrm{~m} / \mathrm{s}$ .
(a) How far do radio signals between the two craft have to travel 3 s later?
(b) How fast are the two craft moving apart at this time?

Question 34

A rope runs through a pulley $3.05 \mathrm{~m}$ off the ground. One end hangs straight down and is attached to a car's engine that is being hoisted. The other end is attached $0.61 \mathrm{~m}$ off the ground to the rear bumper of another car. The car drives away at $4 \mathrm{~km} / \mathrm{h}$ . How fast, in $\mathrm{m} / \mathrm{s}$ , is the rope going through the pulley when the car's rear bumper is $4.88 \mathrm{~m}$ from being under the pulley? The rope is long enough so that the engine is between the ground and the pulley.

Question 35

A movie projector that is $1.2 \mathrm{~m}$ off the ground projects on a screen $50.0 \mathrm{~m}$ away. A woman $1.75 \mathrm{~m}$ tall walks from the screen towards the projector at $1.0 \mathrm{~m} / \mathrm{s}$ . How fast is the woman's shadow getting taller when she is $10.0 \mathrm{~m}$ from the projector?

Question 36

The formula for the volume of fluid $V$ in a spherical tank of radius $r$ when the depth of the fluid $h$ is $V=\frac{\pi h^{2}}{3}(3 r-h)$ A $21.7 \mathrm{~m}$ wide tank is filling with liquid oxygen at a constant rate of $20.5 \mathrm{~L} / \mathrm{s}$ . How fast is the surface of the oxygen rising when the height is $1.06 \mathrm{~m}$ ?

Question 37

A bird flying horizontally at a height of $25 \mathrm{~m}$ and a rate of $10.0 \mathrm{~m} / \mathrm{s}$ passes directly over a scarecrow. Find how fast the distance between the bird and the scarecrow is increasing $5 \mathrm{~s}$ later.

Question 38

A boat with an anchor on the bottom at a depth of $30.0 \mathrm{~m}$ is drifting away from the anchor at $3.00 \mathrm{~m} / \mathrm{s}$ , while the anchor cable slips out at water level. At what rate is the cable leaving the boat when the boat has drifted $10.0 \mathrm{~m}$ away from the spot directly above the anchor? Assume that the cable is straight.

Question 39

One train leaves a station at noon heading east at a rate of $60.0 \mathrm{~km} / \mathrm{h}$ . A second train leaves the same station at 2PM heading north at a rate of $75.0 \mathrm{~km} / \mathrm{h}$ . Find the rate at which they are separating at 5PM.

Question 40

A light is located $20.0 \mathrm{ft}$ above the ground. A person $6.00 \mathrm{ft}$ tall walks away from the light at a rate of $3.00 \mathrm{ft} / \mathrm{s}$ . Find the rate at which the person's shadow is increasing when the person is $10.0 \mathrm{ft}$ from the spot directly under the light.

Question 41

A spherical balloon is decreasing its volume at a rate of $163.87 \mathrm{~cm}^{3} / \mathrm{min}$ . Find the rate at which the radius is decreasing when the volume is $4916.12 \mathrm{~cm}^{3}$ .

Question 42

A circular plate is cooled and contracts so its radius is shrinking by $0.01 \mathrm{~cm} / \mathrm{s}$ . How fast is the area of one face decreasing when the radius is $2.5 \mathrm{~cm}$ ?

Question 43

A $6.00-\mathrm{m}$ ladder is placed against a wall. If the bottom of the ladder is pushed in towards the wall at $0.400 \mathrm{~m} / \mathrm{s}$ , how fast is the top of the ladder moving when the ladder reaches $4.5 \mathrm{~m}$ above the ground?

Question 44

A kite is flying $30 \mathrm{~m}$ above a field. If it stays $30 \mathrm{~m}$ above the field but is moving at $0.3 \mathrm{~m} / \mathrm{s}$ horizontally, how fast is the string being drawn from the reel when the string is $50 \mathrm{~m}$ long?

Question 45

A $3.5-\mathrm{m}$ ladder is leaning against the side of a building. At what rate is the top of the ladder sliding down the building if the bottom of the ladder is $0.80 \mathrm{~m}$ from the base of the building and being pulled away from the building at $2.0 \mathrm{~m} / \mathrm{s}$ ?

Question 46

A spherical snowball is melting at $120 \mathrm{~cm}^{3} / \mathrm{min}$ . At what rate is the surface area decreasing at when the radius is $15 \mathrm{~cm}$ ?

Question 47

A light is on the ground $70.0 \mathrm{~m}$ away from a wall. At what rate will a $1.80-\mathrm{m}$ tall person's shadow be increasing when the person is $20.0 \mathrm{~m}$ from wall and walking away from the wall at $5.00 \mathrm{~m} / \mathrm{s}$ .

Question 48

Sand is being piled on the ground in a conical shape at a rate of $4.50 \mathrm{~cm}^{3} / \mathrm{s}$ . At what rate is the radius of the pile increasing at when the height is $12.0 \mathrm{~cm}$ and the radius is $6.00 \mathrm{~cm}$ ? The height is increasing at twice the rate of the radius.

Question 49

A metal bar $4.00 \mathrm{~cm}$ by $6.00 \mathrm{~cm}$ by $48.0 \mathrm{~cm}$ is being heated such that each length is increasing at 0.05 $\mathrm{cm} / \mathrm{s}$ . At what rate is the volume increasing?

Question 50

A pebble is dropped into a calm pond causing a series of circular ripples. The radius of the outer ripple is increasing at $0.700 \mathrm{~m} / \mathrm{s}$ . How fast is the area increasing at $5.00 \mathrm{~s}$ ?

Question 51

A ship is travelling at $12.0 \mathrm{~km} / \mathrm{h}, 2.00 \mathrm{~km}$ parallel to shore. The ship passes a light house, what is the straight-line distance between the ship and the light house 30 minutes later?

Question 52

Split the number 15 into two parts so that the product of one part and the other is maximized.

Question 53

A rectangular area with a certain size is to be enclosed on three sides by a fence and on one side by an existing building. Find the ratio of the sides of the area that minimizes the fence needed.

Question 54

Find the area of the largest rectangle with sides parallel to the coordinate axes which can be inscribed in the figure bounded by the parabolas $2 x=y^{2}-10$ and $4 x=16-2 y^{2}$ .

Question 55

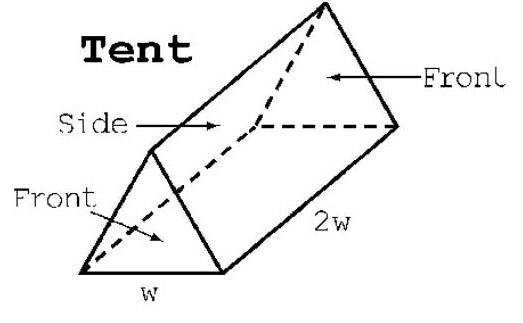
The tent is in the shape of a triangular prism, with both ends covered, but with no bottom. It has a rectangular base with a width that is half its length. The tent must have a volume of $58.0 \mathrm{~m}^{3}$ . Find the width of the tent that minimizes the surface area of the tent.

Question 56

A point is on a $4 \mathrm{~m}$ long line between Light $\mathrm{A}$ and Light $\mathrm{B}$ . Light $\mathrm{B}$ is 3 times as bright as Light $\mathrm{A}$ . The intensity of light at a point is proportional to the brightness of the light divided by the square of the distance from the light to the point. Find the distance of the point from A that minimizes the intensity of the light at the point.

Question 57

Separate the number 200 into two parts such that the sum of one part times 60 and square of the second part is a minimum.

Question 58

Suppose you want to fence three sides of rectangular region where one side is bordered by a river. Find the dimensions for the maximum possible area if you have material for only $140 \mathrm{~m}$ of fence.

Question 59

Find the maximum area for an isosceles triangle with a perimeter of $76.2 \mathrm{~cm}$ .

Question 60

A car is on a road traveling due north at $56.3 \mathrm{~km} / \mathrm{h}$ and a motorcycle is traveling on another road due west at $64.37 \mathrm{~km} / \mathrm{h}$ . The car is $24.14 \mathrm{~km}$ from the point where the roads meet and the motorcycle is $8.00 \mathrm{~km}$ past that point. What is the closest that the two vehicles get?

Question 61

Find the volume of the largest right cylinder that can be inscribed in a cone of height $20.00 \mathrm{~cm}$ . and a base radius of $15.00 \mathrm{~cm}$ .

Question 62

The cost of manufacturing a crankshaft per hour follows the equation $c=2 x^{2}-8 x+2$ where $\mathrm{x}$ is the number of crankshafts. What is the optimum number of crankshafts to minimize production costs?

Question 63

What is the maximum volume for a lidless box created from a rectangular piece of sheet metal measuring $50.0 \mathrm{~cm}$ by $80.0 \mathrm{~cm}$ ? (The box is created by cutting equal squares out of each corner and folding up the sides).

Question 64

A rectangular hardwood dance floor has one border against a carpeted area and the rest bordering tile. If the border along the carpeted edge costs twice as much as the border with the tiles, what are the dimensions of a $80.0 \mathrm{~m}^{2}$ dance floor with minimum border costs?

Question 65

What is the maximum volume of cylindrical tin can that can be made from $750.0 \mathrm{~cm}^{2}$ of metal?

Question 66

What is the largest area that can be enclosed by fence? We have $18 \overline{0} \mathrm{~m}$ of fence and there is a preexisting fence on one side.

Question 67

What dimensions of a rectangular beam will give the maximum strength? The beam is to be cut from a circular log with a diameter of $80.0 \mathrm{~cm}$ ? $\left(S=k x y^{2}\right)$

Question 68

What value of $x$ will give the maximum efficiency of a screw with a coefficient of friction $\mu=0.82$ ?
$E=\frac{x-\mu x^{2}}{x+\mu}$

Question 69

What is the minimum amount of metal needed to make a $300000-\mathrm{cm}^{3}$ cylindrical drum? Express our answer to the nearest whole square centimetre.

Question 70

The power $(\mathrm{W})$ delivered to a load by a $40 \mathrm{~V}$ source with internal resistance of $5 \Omega$ is $P=40 i-5 i^{2}$ . What current will give the maximum power?

Question 71

A window is composed of a rectangle with a semicircle above. If the perimeter is $16.0 \mathrm{~m}$ , what dimensions will make the area of the window a maximum?