Deck 4: Exponential and Logarithmic Functions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/192
Play
Full screen (f)
Deck 4: Exponential and Logarithmic Functions
1
Classify the function as a linear, quadratic, or exponential.
-f
A) Linear
B) Exponential
C) Quadratic
-f
A) Linear
B) Exponential
C) Quadratic
Linear
2
Classify the function as a linear, quadratic, or exponential.
-
A) Quadratic
B) Exponential
C) Linear
-
A) Quadratic
B) Exponential
C) Linear
Linear
3
Classify the function as a linear, quadratic, or exponential.
-
A) Exponential
B) Quadratic
C) Linear
-
A) Exponential
B) Quadratic
C) Linear
Quadratic
4
Classify the function as a linear, quadratic, or exponential.
-
A) Exponential
B) Quadratic
C) Linear
-
A) Exponential
B) Quadratic
C) Linear

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
5
Classify the function as a linear, quadratic, or exponential.
-
A) Linear
B) Exponential
C) Quadratic
-
A) Linear
B) Exponential
C) Quadratic

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
6
Classify the function as a linear, quadratic, or exponential.
-
A) Exponential
B) Quadratic
C) Linear
-
A) Exponential
B) Quadratic
C) Linear

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
7
Classify the function as a linear, quadratic, or exponential.
-
A) Quadratic
B) Linear
C) Exponential
-
A) Quadratic
B) Linear
C) Exponential

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
8
without graphing, describe the shape of the graph of the function and complete the ordered pairs and ,
-
A) The graph lies below the -axis, falls from right to left, with the positive -axis as a horizontal asymptote; and .
B) The graph lies below the -axis, falls from left to right, with the positive -axis as a horizontal asymptote; and .
C) The graph lies above the -axis, falls from right to left, with the positive -axis as a horizontal asymptote; and .
D) The graph lies above the -axis, falls from left to right, with the positive -axis as a horizontal asymptote; and .
-
A) The graph lies below the -axis, falls from right to left, with the positive -axis as a horizontal asymptote; and .
B) The graph lies below the -axis, falls from left to right, with the positive -axis as a horizontal asymptote; and .
C) The graph lies above the -axis, falls from right to left, with the positive -axis as a horizontal asymptote; and .
D) The graph lies above the -axis, falls from left to right, with the positive -axis as a horizontal asymptote; and .

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
9
without graphing, describe the shape of the graph of the function and complete the ordered pairs and ,
-
A) The graph lies below the -axis, falls from left to right, with the negative -axis as a horizontal asy mptote; and .
B) The graph lies above the -axis, falls from right to left, with the negative -axis as a horizontal asymptote; and .
C) The graph lies below the -axis, falls from right to left, with the negative -axis as a horizontal asymptote; and .
D) The graph lies above the -axis, falls from left to right, with the negative -axis as a horizontal asymptote; and .
-
A) The graph lies below the -axis, falls from left to right, with the negative -axis as a horizontal asy mptote; and .
B) The graph lies above the -axis, falls from right to left, with the negative -axis as a horizontal asymptote; and .
C) The graph lies below the -axis, falls from right to left, with the negative -axis as a horizontal asymptote; and .
D) The graph lies above the -axis, falls from left to right, with the negative -axis as a horizontal asymptote; and .

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
10
without graphing, describe the shape of the graph of the function and complete the ordered pairs and ,
-
A) The graph lies above the -axis, falls from left to right, with the positive -axis as a horizontal asymptote; and .
B) The graph lies above the -axis, falls from left to right, with the negative -axis as a horizontal asymptote; and .
C) The graph lies above the -axis, falls from right to left, with the negative -axis as a horizontal asymptote; and .
D) The graph lies above the -axis, falls from right to left, with the positive -axis as a horizontal asymptote; and .
-
A) The graph lies above the -axis, falls from left to right, with the positive -axis as a horizontal asymptote; and .
B) The graph lies above the -axis, falls from left to right, with the negative -axis as a horizontal asymptote; and .
C) The graph lies above the -axis, falls from right to left, with the negative -axis as a horizontal asymptote; and .
D) The graph lies above the -axis, falls from right to left, with the positive -axis as a horizontal asymptote; and .

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
11
without graphing, describe the shape of the graph of the function and complete the ordered pairs and ,
-
A) The graph lies above the -axis, falls from left to right, with the negative -axis as a horizontal asymptote; and .
B) The graph lies below the -axis, rises from left to right, with the negative -axis as a horizontal asymptote; and .
C) The graph lies above the -axis, rises from left to right, with the negative -axis as a horizontal asymptote; and .
D) The graph lies below the -axis, falls from right to left, with the negative -axis as a horizontal asymptote; and .
-
A) The graph lies above the -axis, falls from left to right, with the negative -axis as a horizontal asymptote; and .
B) The graph lies below the -axis, rises from left to right, with the negative -axis as a horizontal asymptote; and .
C) The graph lies above the -axis, rises from left to right, with the negative -axis as a horizontal asymptote; and .
D) The graph lies below the -axis, falls from right to left, with the negative -axis as a horizontal asymptote; and .

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
12
without graphing, describe the shape of the graph of the function and complete the ordered pairs and ,
-
A) The graph lies below the -axis, falls from right to left, with the positive -axis as a horizontal asymptote; and .
B) The graph lies above the -axis, rises from right to left, with the negative -axis as a horizontal asymptote; and .
C) The graph lies above the -axis, rises from left to right, with the negative -axis as a horizontal asymptote; and .
D) The graph lies below the -axis, falls from left to right, with the positive -axis as a horizontal asymptote; and .
-
A) The graph lies below the -axis, falls from right to left, with the positive -axis as a horizontal asymptote; and .
B) The graph lies above the -axis, rises from right to left, with the negative -axis as a horizontal asymptote; and .
C) The graph lies above the -axis, rises from left to right, with the negative -axis as a horizontal asymptote; and .
D) The graph lies below the -axis, falls from left to right, with the positive -axis as a horizontal asymptote; and .

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
13
Graph the function.
-
A)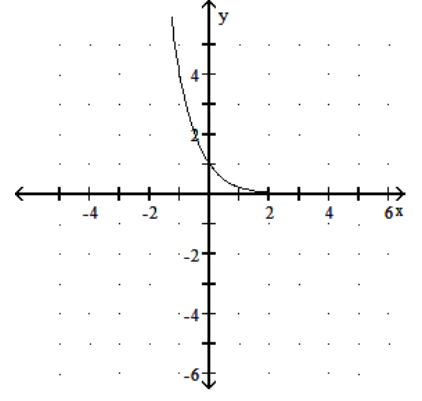
B)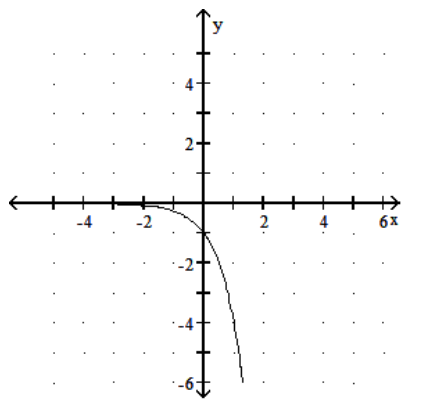
C)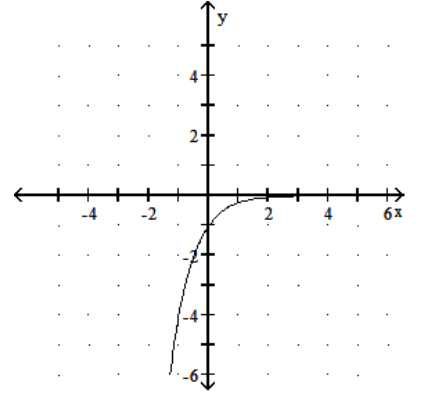
D)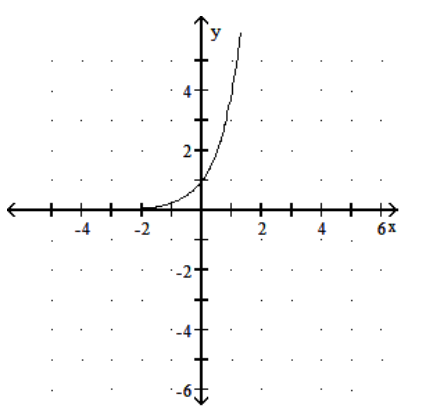
-

A)

B)

C)
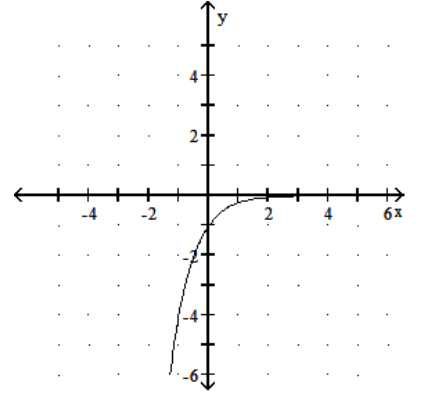
D)


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
14
Graph the function.
-
A)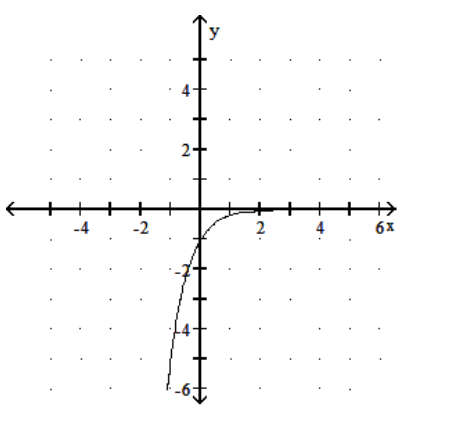
B)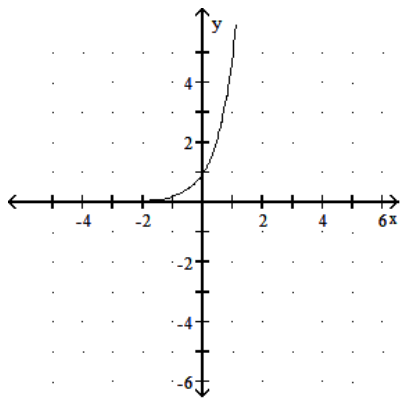
C)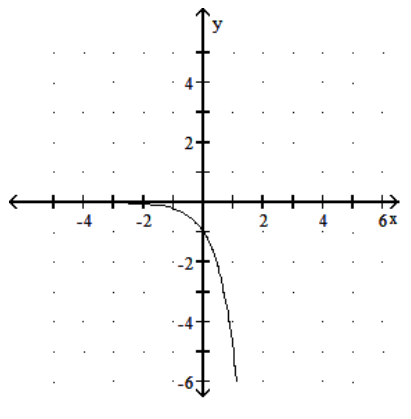
D)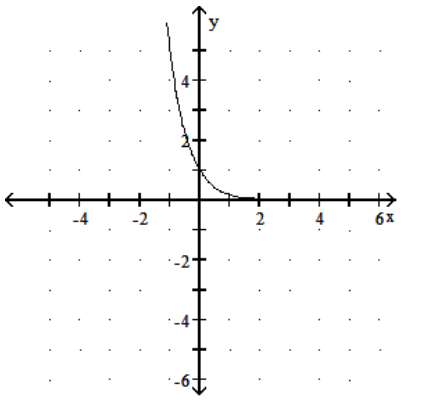
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
15
Graph the function.
-
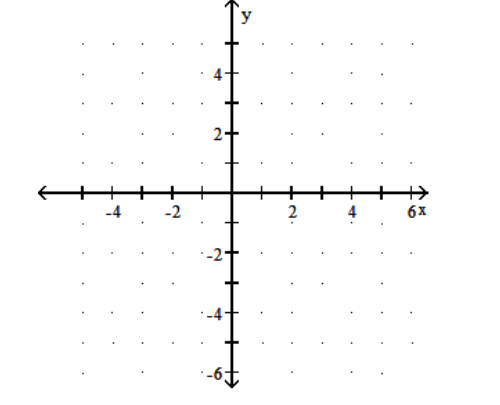
A)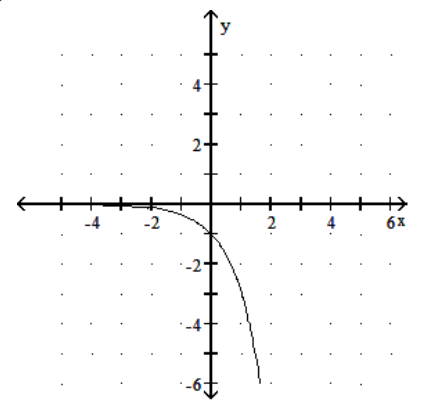
B)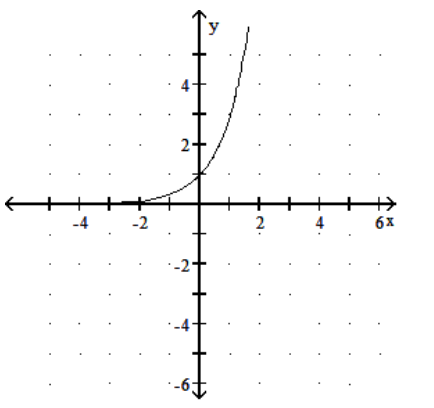
C)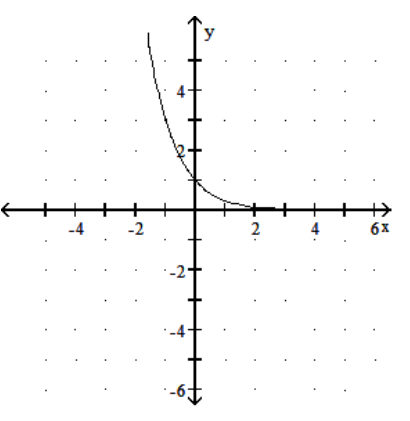
D)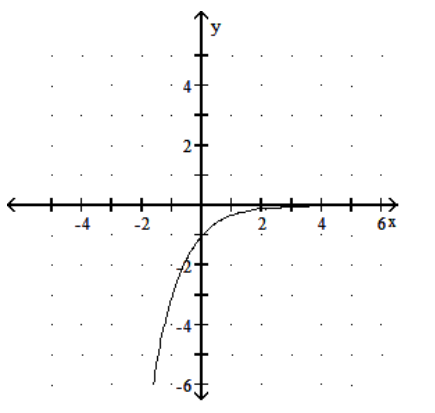
-

A)

B)

C)

D)
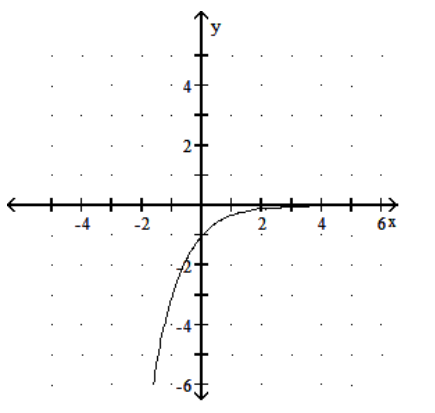

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
16
Graph the function.
-
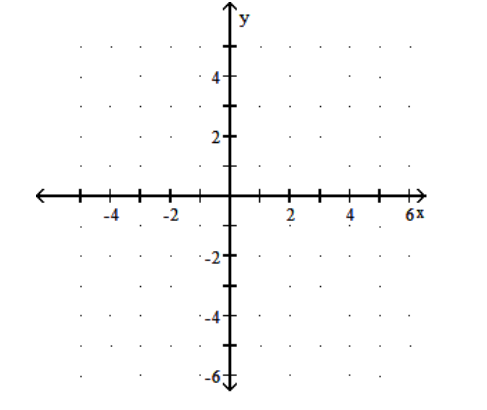
A)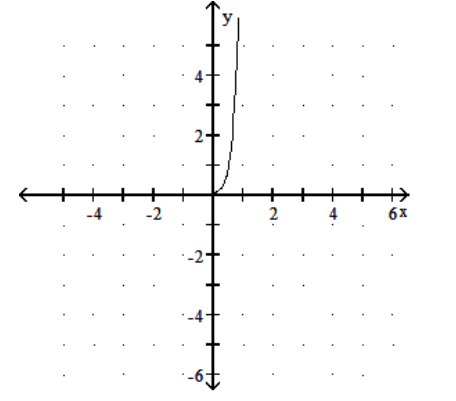
B)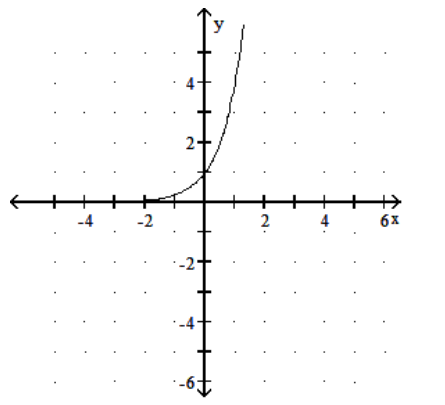
C)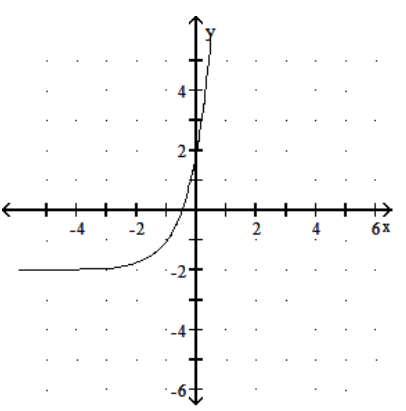
D)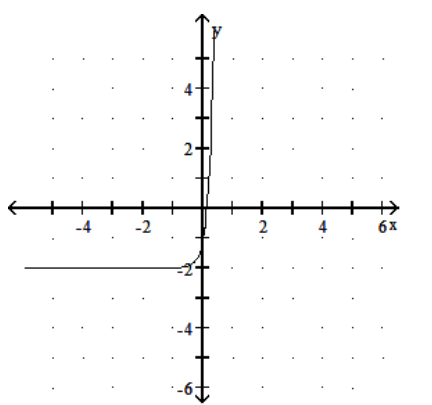
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
17
Graph the function.
-
A)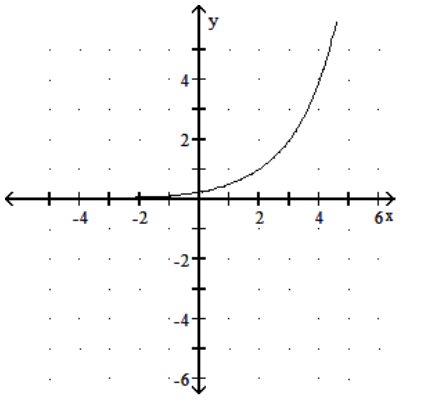
B)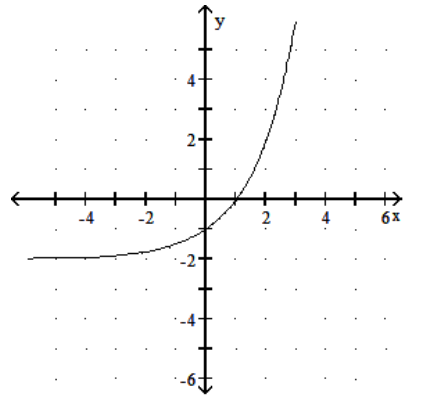
C)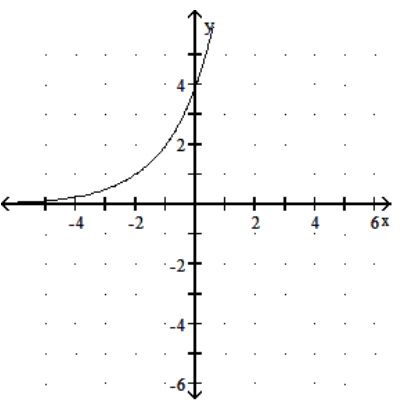
D)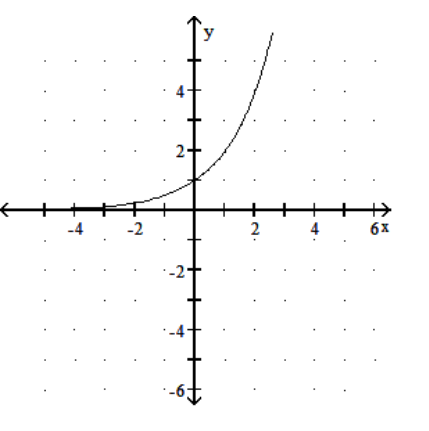
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
18
Graph the function.
-
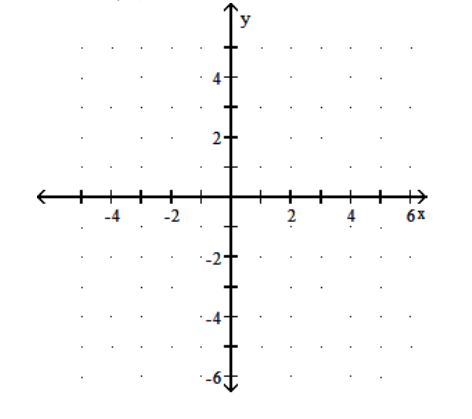
A)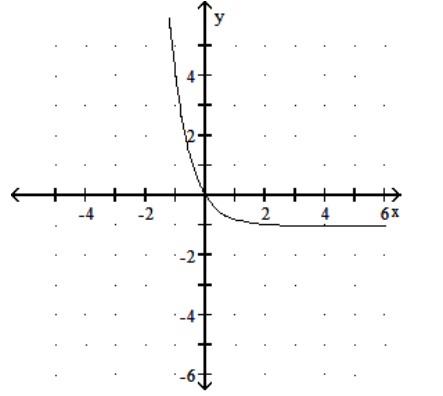
B)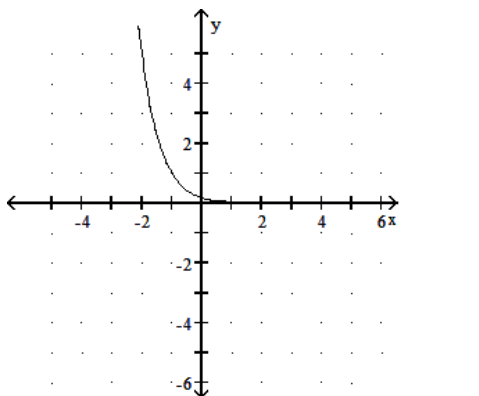
C)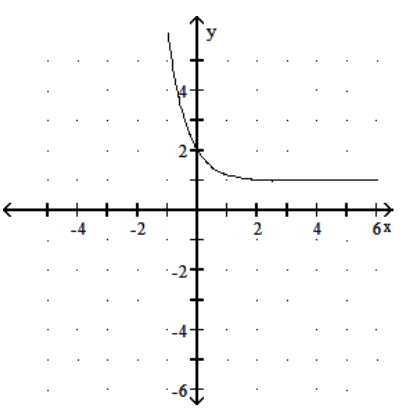
D)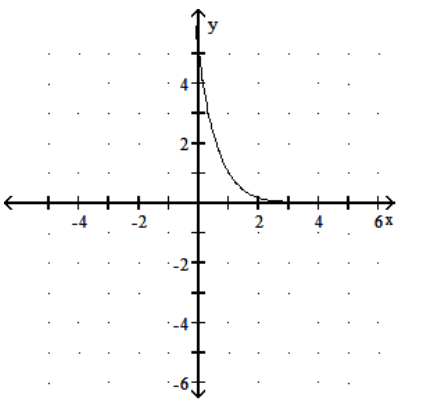
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
19
Graph the function.
-
A)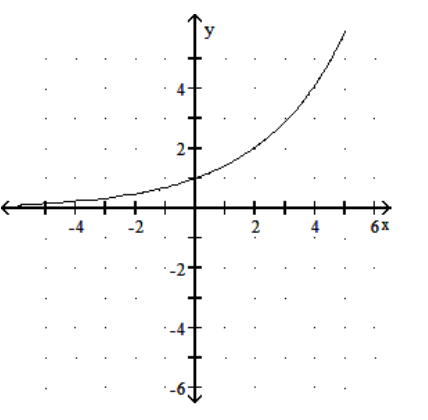
B)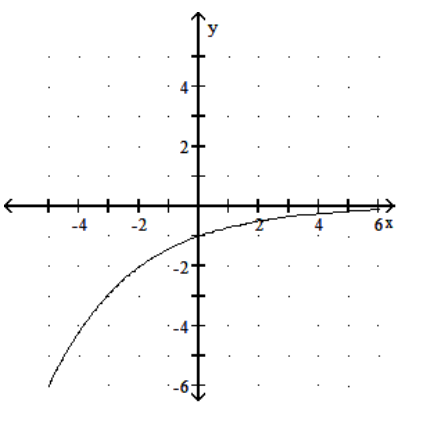
C)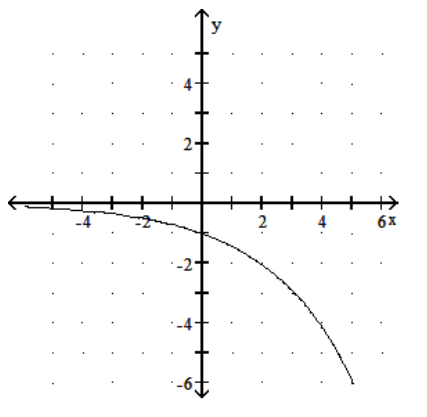
D)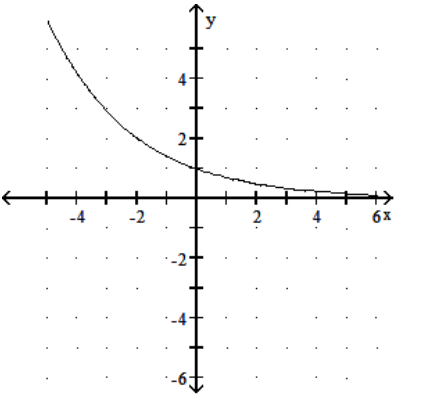
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
20
Graph the function.
-
A)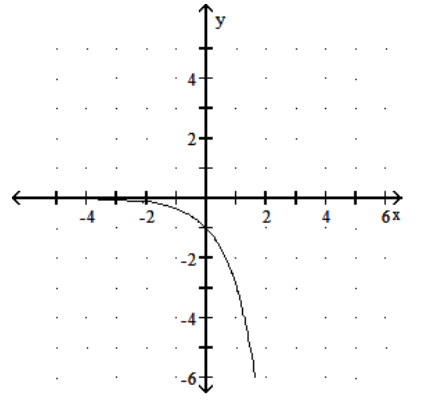
B)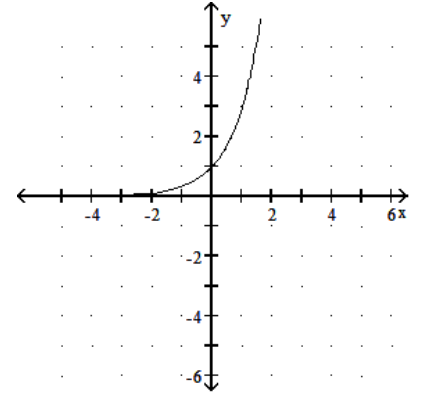
C)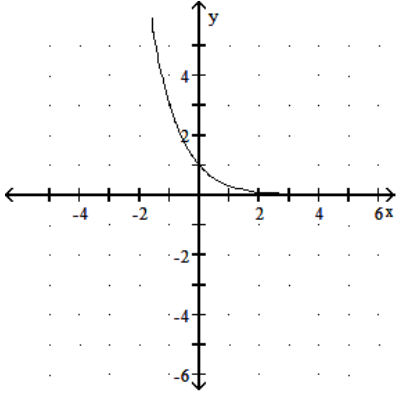
D)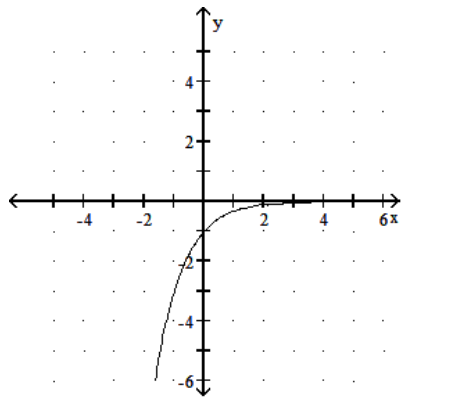
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
21
Graph the function.
-
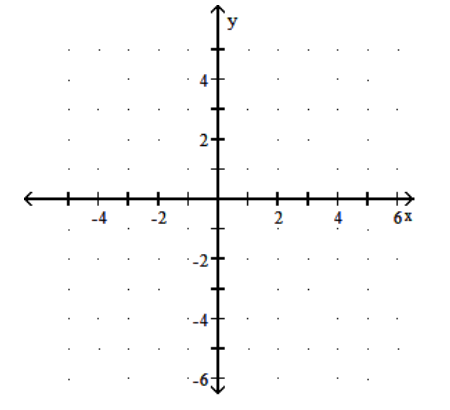
A)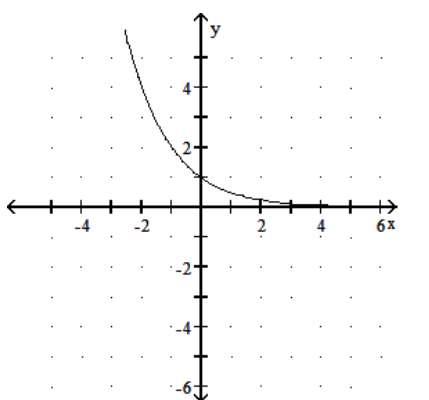
B)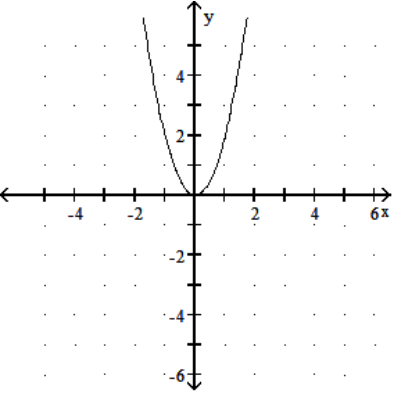
C)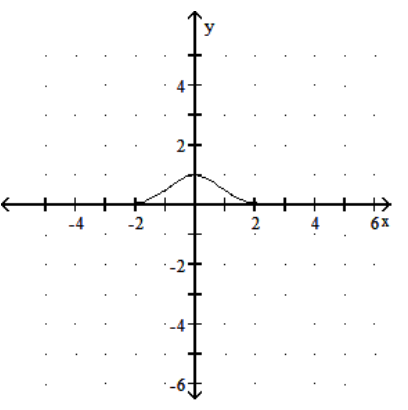
D)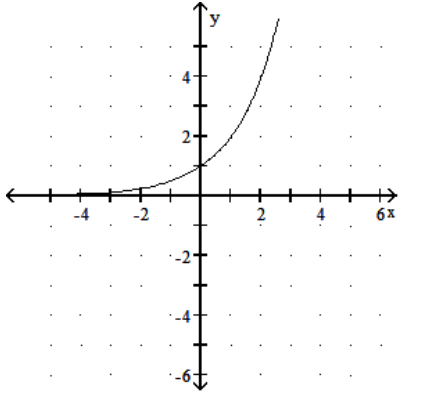
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
22
Graph the function.
-
A)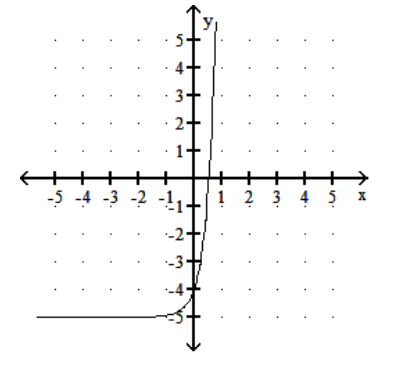
B)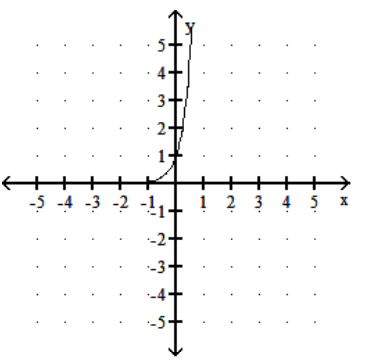
C)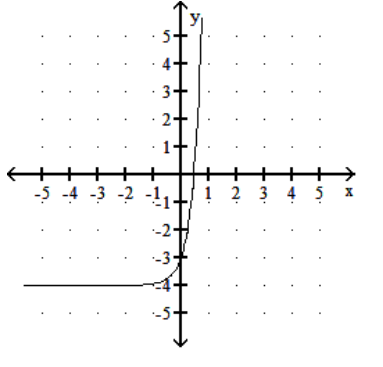
D)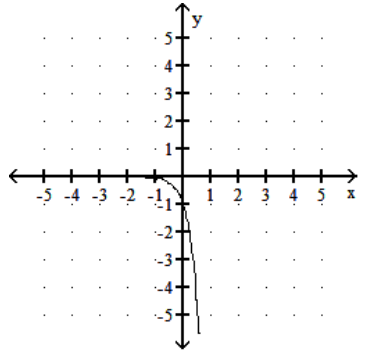
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
23
Provide an appropriate response.
-In the given figure, the graphs of for are given. Identify the graph of .
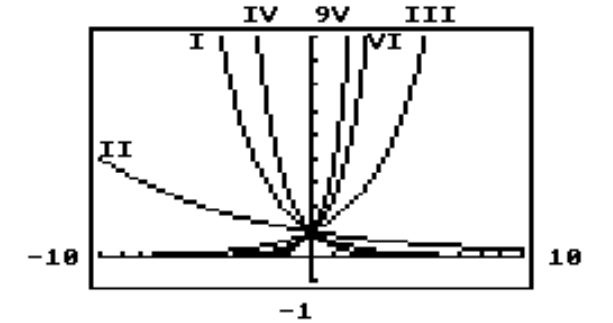
A) V
B) III
C) VI
D) I
-In the given figure, the graphs of for are given. Identify the graph of .

A) V
B) III
C) VI
D) I

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
24
Provide an appropriate response.
-The graph of an exponential function is given. Which of the following is the correct equation of the function?
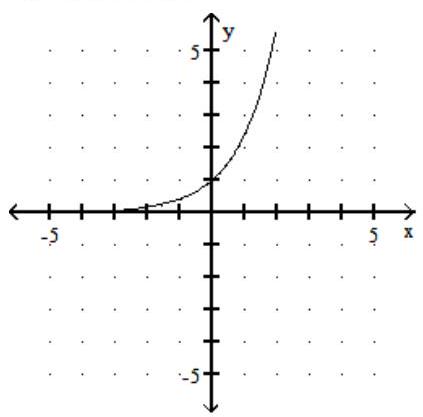
A)
B)
C)
D)
-The graph of an exponential function is given. Which of the following is the correct equation of the function?

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
25
Provide an appropriate response.
-The graph of an exponential function is given. Which of the following is the correct equation of the function?
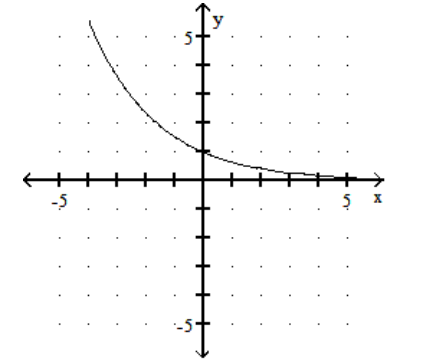
A)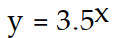
B)
C)
D)
-The graph of an exponential function is given. Which of the following is the correct equation of the function?

A)
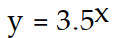
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
26
Provide an appropriate response.
-The graph of an exponential function is given. Which of the following is the correct equation of the function?
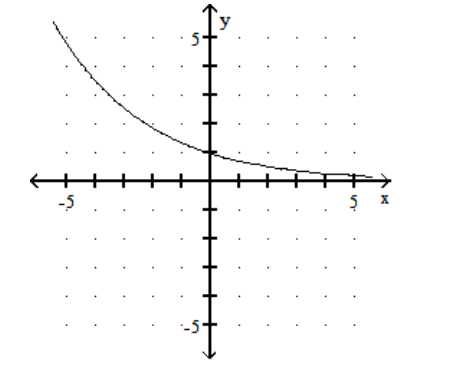
A)
B)
C)
D)
-The graph of an exponential function is given. Which of the following is the correct equation of the function?

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
27
Provide an appropriate response.
-The graph of an exponential function is given. Which of the following is the correct equation of the function?
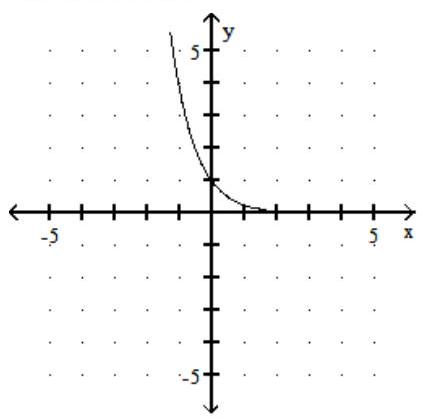
A)
B)
C)
D)
-The graph of an exponential function is given. Which of the following is the correct equation of the function?

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
28
Write the word or phrase that best completes each statement or answers the question.
-
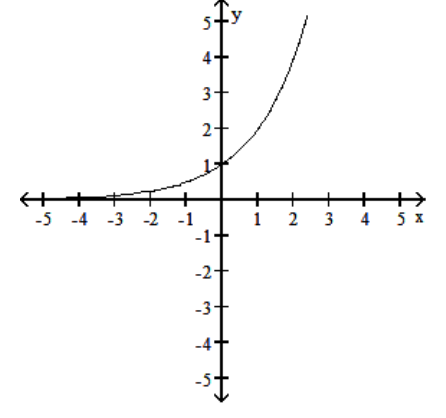 The graph of an exponential function with base a is given. Is a or is ? Explain how you arrived at your answer. Give the domain and range of .
The graph of an exponential function with base a is given. Is a or is ? Explain how you arrived at your answer. Give the domain and range of .
-
 The graph of an exponential function with base a is given. Is a or is ? Explain how you arrived at your answer. Give the domain and range of .
The graph of an exponential function with base a is given. Is a or is ? Explain how you arrived at your answer. Give the domain and range of . 
Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
29
Write the word or phrase that best completes each statement or answers the question.
-
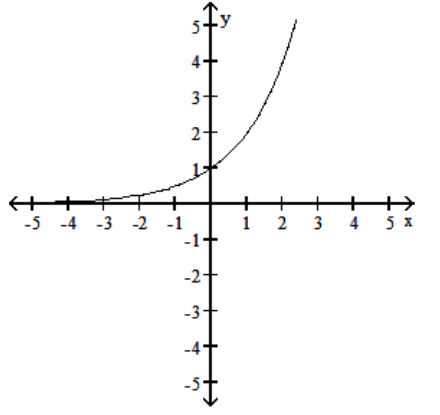 The graph of an exponential function with base is given. Sketch the graph of . Give the domain and range of .
The graph of an exponential function with base is given. Sketch the graph of . Give the domain and range of .
-
 The graph of an exponential function with base is given. Sketch the graph of . Give the domain and range of .
The graph of an exponential function with base is given. Sketch the graph of . Give the domain and range of . 
Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
30
Write the word or phrase that best completes each statement or answers the question.
-
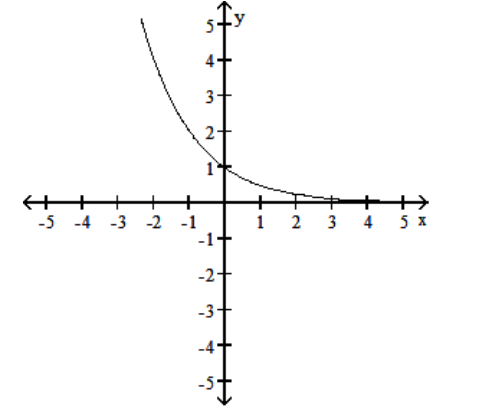 The graph of an exponential function with base a is given. Sketch the graph of . Give the domain and range of .
The graph of an exponential function with base a is given. Sketch the graph of . Give the domain and range of .
-
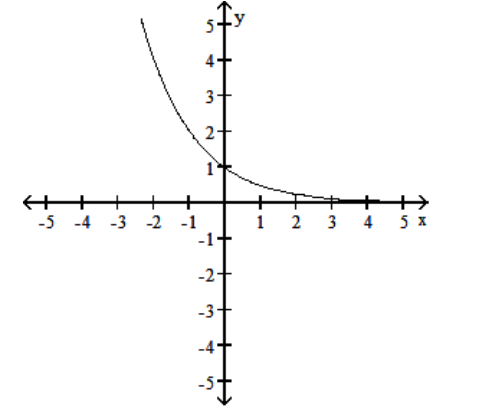 The graph of an exponential function with base a is given. Sketch the graph of . Give the domain and range of .
The graph of an exponential function with base a is given. Sketch the graph of . Give the domain and range of . 
Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
31
Write the word or phrase that best completes each statement or answers the question.
-
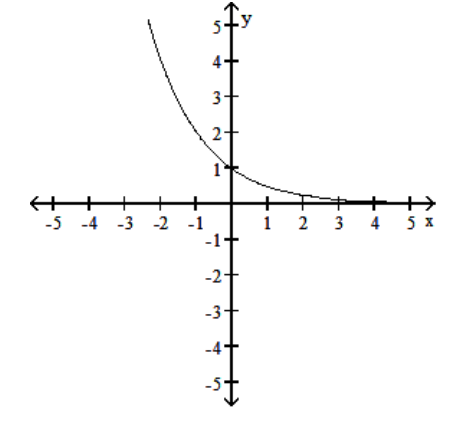 The graph of an exponential function with base a is given. Sketch the graph of . Give the domain and range of .
The graph of an exponential function with base a is given. Sketch the graph of . Give the domain and range of .
-
 The graph of an exponential function with base a is given. Sketch the graph of . Give the domain and range of .
The graph of an exponential function with base a is given. Sketch the graph of . Give the domain and range of . 
Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
32
Write the word or phrase that best completes each statement or answers the question.
-
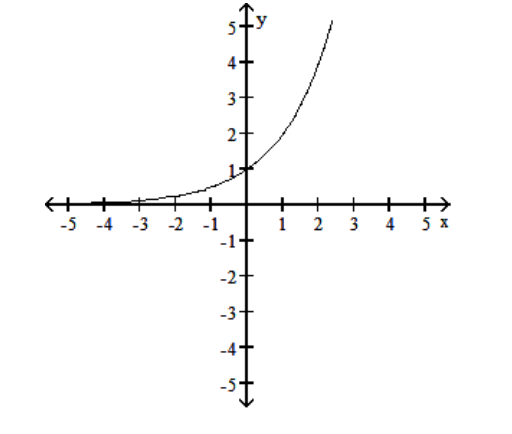 The graph of an exponential function with base a is given. Sketch the graph of . Give the domain and range of .
The graph of an exponential function with base a is given. Sketch the graph of . Give the domain and range of .
-
 The graph of an exponential function with base a is given. Sketch the graph of . Give the domain and range of .
The graph of an exponential function with base a is given. Sketch the graph of . Give the domain and range of . 
Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
33
Solve the problem.
-An economist predicts that the buying power of a dollar years from now will decrease according to the formula . How much will today's dollar be worth in 5 years? Round the answer to the nearest cent.
A)\$ 1.97
B)
C)
D)
-An economist predicts that the buying power of a dollar years from now will decrease according to the formula . How much will today's dollar be worth in 5 years? Round the answer to the nearest cent.
A)\$ 1.97
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
34
Solve the problem.
-The number of dislocated electric impulses per cubic inch in a transformer increases when lightning strikes by , where is the time in milliseconds of the lightning strike. Find the number of dislocated impulses at and .
A)
B)
C)
D)
-The number of dislocated electric impulses per cubic inch in a transformer increases when lightning strikes by , where is the time in milliseconds of the lightning strike. Find the number of dislocated impulses at and .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
35
Solve the problem.
-The number of dislocated electric impulses per cubic inch in a transformer when lightning strikes is given by , where is the time in milliseconds of the lightning strike. Find the number of dislocated impulses at and .
A)
B)
C)
D)
-The number of dislocated electric impulses per cubic inch in a transformer when lightning strikes is given by , where is the time in milliseconds of the lightning strike. Find the number of dislocated impulses at and .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
36
Solve the problem.
-The amount of particulate matter left in solution during a filtering process is given by the equation , where is the number of filtering steps. Find the amounts left for and . (Round to the nearest whole number.)
A) 200,13
B) 400,13
C) 200,6
D) 200,3200
-The amount of particulate matter left in solution during a filtering process is given by the equation , where is the number of filtering steps. Find the amounts left for and . (Round to the nearest whole number.)
A) 200,13
B) 400,13
C) 200,6
D) 200,3200

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
37
Solve the problem.
-The number of bacteria growing in an incubation culture increases with time according to , where is time in days. Find the number of bacteria when and .
A)
B)
C)
D)
-The number of bacteria growing in an incubation culture increases with time according to , where is time in days. Find the number of bacteria when and .
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
38
Solve the problem.
-Suppose the amount of a radioactive element remaining in a sample of 100 milligrams after years can be described by . How much is remaining after 194 years? Round the answer to the nearest hundredth of a milligram.
A) 0.04 milligrams
B) 2597.83 milligrams
C) 325.73 milligrams
D) 3.85 milligrams
-Suppose the amount of a radioactive element remaining in a sample of 100 milligrams after years can be described by . How much is remaining after 194 years? Round the answer to the nearest hundredth of a milligram.
A) 0.04 milligrams
B) 2597.83 milligrams
C) 325.73 milligrams
D) 3.85 milligrams

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
39
Solve the problem.
-The decay of of an isotope is given by , where is time in years. Find the amount left after 4 years.
A) 259
B) 253
C) 130
D) 281
-The decay of of an isotope is given by , where is time in years. Find the amount left after 4 years.
A) 259
B) 253
C) 130
D) 281

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
40
Solve the problem.
-Use the formula . A bacterial culture has an initial population of 500. If its population grows to 7000 in 6 hours, what will it be at the end of 8 hours?
A) 4838
B) 51,714
C) 1117
D) 16,723
-Use the formula . A bacterial culture has an initial population of 500. If its population grows to 7000 in 6 hours, what will it be at the end of 8 hours?
A) 4838
B) 51,714
C) 1117
D) 16,723

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
41
Solve the problem.
-Use the formula . A bacterial culture has an initial population of 10,000 . If its population declines to 3000 in 2 hours, what will it be at the end of 4 hours?
A) 450
B) 900
C) 4481
D) 3500
-Use the formula . A bacterial culture has an initial population of 10,000 . If its population declines to 3000 in 2 hours, what will it be at the end of 4 hours?
A) 450
B) 900
C) 4481
D) 3500

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
42
Solve the problem.
-The population of a particular city is increasing at a rate proportional to its size. It follows the function where is a constant and is the time in years. If the current population is 29,000 , in how many years is the population expected to be 72,500 ?
A) 79 year(s)
B) 5 years(s)
C) 6 year(s)
D) 11 year(s)
-The population of a particular city is increasing at a rate proportional to its size. It follows the function where is a constant and is the time in years. If the current population is 29,000 , in how many years is the population expected to be 72,500 ?
A) 79 year(s)
B) 5 years(s)
C) 6 year(s)
D) 11 year(s)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
43
Solve the problem.
-The number of books in a small library increases according to the function , where is measured in years. How many books will the library have after 3 years?
A) 5226
B) 4299
C) 3048
D) 7019
-The number of books in a small library increases according to the function , where is measured in years. How many books will the library have after 3 years?
A) 5226
B) 4299
C) 3048
D) 7019

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
44
Solve the problem.
-The sales of a mature product (one which has passed its peak) will decline by the function , where is time in years. Find the sales after 9 years if and .
A) 7957
B) 227,497
C) 15,913
D) 64,530
-The sales of a mature product (one which has passed its peak) will decline by the function , where is time in years. Find the sales after 9 years if and .
A) 7957
B) 227,497
C) 15,913
D) 64,530

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the problem.
-The growth in the population of a certain rodent at a dump site fits the exponential function , where is the number of years since 1967. Estimate the population in the year 2000.
A) 580
B) 1182
C) 1159
D) 611
-The growth in the population of a certain rodent at a dump site fits the exponential function , where is the number of years since 1967. Estimate the population in the year 2000.
A) 580
B) 1182
C) 1159
D) 611

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
46
Solve the problem.
-The decay of of an isotope is given by , where is time in years. Find the amount left after 13 years.
A) 136
B) 161
C) 134
D) 68
-The decay of of an isotope is given by , where is time in years. Find the amount left after 13 years.
A) 136
B) 161
C) 134
D) 68

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
47
Find an exponential function of theform to model the given data.
-Under ideal conditions, a population of rabbits has an exponential growth rate of per day. Consider an initial population of 900 rabbits. Find the exponential growth function.
A)P
B)
C)P
D)
-Under ideal conditions, a population of rabbits has an exponential growth rate of per day. Consider an initial population of 900 rabbits. Find the exponential growth function.
A)P
B)
C)P
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
48
Find an exponential function of theform to model the given data.
-In 1985, the number of female athletes participating in Summer Olympic-Type Games was 550. In 1996, about 3550 participated in the Summer Olympics in Atlanta. Assuming that and that the exponential model applies, find the value of rounded to the hundredths place, and write the function.
A)
B)
C)
D)
-In 1985, the number of female athletes participating in Summer Olympic-Type Games was 550. In 1996, about 3550 participated in the Summer Olympics in Atlanta. Assuming that and that the exponential model applies, find the value of rounded to the hundredths place, and write the function.
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
49
Solve the problem.
-Use a graphing calculator to predict about how many books will have been read in the eighth grade.
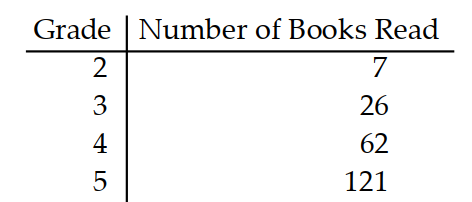
A) 500
B) 1000
C) 3000
D) 2000
-Use a graphing calculator to predict about how many books will have been read in the eighth grade.
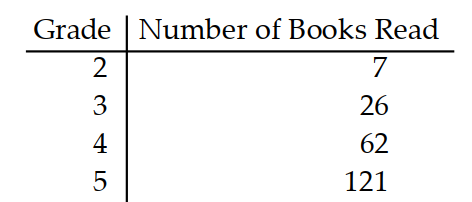
A) 500
B) 1000
C) 3000
D) 2000

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
50
Solve the problem.
-Use a graphing calculator to predict about how many widgets will be produced in 2004.
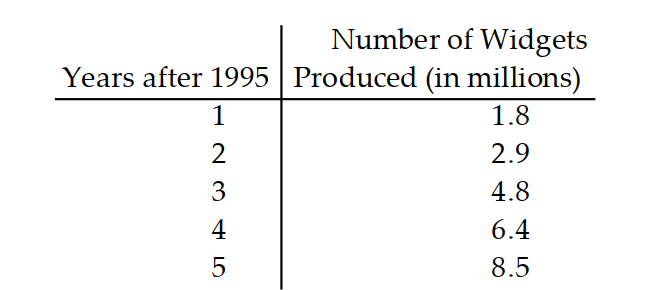
A) 11 million
B) 60 million
C) 20 million
D) 44 million
-Use a graphing calculator to predict about how many widgets will be produced in 2004.

A) 11 million
B) 60 million
C) 20 million
D) 44 million

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
51
Solve the problem.
-Use a graphing calculator to predict what income the company should expect in its seventh year of operation.
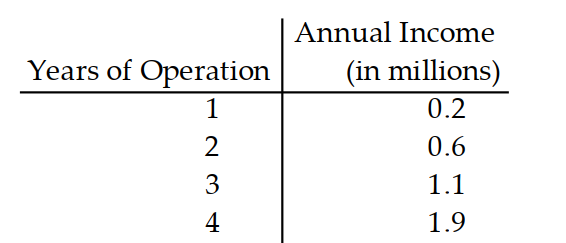
A) 5-7 million
B) 2-3 million
C) 30-40 million
D) 10-20 million
-Use a graphing calculator to predict what income the company should expect in its seventh year of operation.

A) 5-7 million
B) 2-3 million
C) 30-40 million
D) 10-20 million

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
52
Solve.
-In a town whose population is 3500 , a disease creates an epidemic. The number of people infected days after the disease has begun is given by the function
Find the number infected after 16 days.
A) 3502
B) 3498
C) 3500
D) 3503
-In a town whose population is 3500 , a disease creates an epidemic. The number of people infected days after the disease has begun is given by the function
Find the number infected after 16 days.
A) 3502
B) 3498
C) 3500
D) 3503

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
53
Solve.
-In recent years, many states have passed laws against smoking in public buildings. The total number of states that have passed a no smoking in public buildings law, years after 1985 is given by the function
How many states had passed the law in 1985 ?
A) 2.5
B) 1.25
C) 0.25
D) 0
-In recent years, many states have passed laws against smoking in public buildings. The total number of states that have passed a no smoking in public buildings law, years after 1985 is given by the function
How many states had passed the law in 1985 ?
A) 2.5
B) 1.25
C) 0.25
D) 0

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
54
Solve.
-A lake is stocked with 578 fish of a new variety. The size of the lake, the availability of food, and the number of other fish restrict growth in the lake to a limiting value of 3612. The population of fish in the lake after time , in months, is given by the function
Find the population after 20 months.
A) 3597
B) 3582
C) 3572
D) 3592
-A lake is stocked with 578 fish of a new variety. The size of the lake, the availability of food, and the number of other fish restrict growth in the lake to a limiting value of 3612. The population of fish in the lake after time , in months, is given by the function
Find the population after 20 months.
A) 3597
B) 3582
C) 3572
D) 3592

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
55
Convert to exponential form.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
56
Convert to exponential form.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
57
Convert to exponential form.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
58
Convert to exponential form.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
59
Write in logarithmic form.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
60
Write in logarithmic form.
-
A)
B)
C) .
D)
-
A)
B)
C) .
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
61
Write in logarithmic form.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
62
Write in logarithmic form.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
63
Write in logarithmic form.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
64
Find the value of the expression.
-
A) 27
B) 9
C) 3
D) 729
-
A) 27
B) 9
C) 3
D) 729

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
65
Find the value of the expression.
-
A) 5
B) 10
C) 2
D) 25
-
A) 5
B) 10
C) 2
D) 25

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
66
Find the value of the expression.
-
A) 1
B) -1
C) 4
D) 0
-
A) 1
B) -1
C) 4
D) 0

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
67
Find the value of the expression.
-
A) 9
B) -9
C) 2
D) -2
-
A) 9
B) -9
C) 2
D) -2

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
68
Find the value of the expression.
-
A) -1
B) 1
C) 0
D) 10
-
A) -1
B) 1
C) 0
D) 10

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
69
Find the value of the expression.
-
A) 81
B) -3
C) 3
D) -81
-
A) 81
B) -3
C) 3
D) -81

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
70
Find the value of the expression.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
71
Find the value of the expression.
-ln e
A) e
B) -1
C) 1
D) 0
-ln e
A) e
B) -1
C) 1
D) 0

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
72
Find the value of the expression.
-
A) 1
B) 0
C)
D) -1
-
A) 1
B) 0
C)
D) -1

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
73
Use a calculator to evaluate the logarithm.
-
A) 2.4456
B) 2.4487
C) 5.6348
D) 2.4472
-
A) 2.4456
B) 2.4487
C) 5.6348
D) 2.4472

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
74
Use a calculator to evaluate the logarithm.
-
A) 0.5250
B) 0.5378
C) 0.5502
D) 1.2384
-
A) 0.5250
B) 0.5378
C) 0.5502
D) 1.2384

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
75
Use a calculator to evaluate the logarithm.
-
A) 8.3366
B) 3.6216
C) 3.6195
D) 3.6206
-
A) 8.3366
B) 3.6216
C) 3.6195
D) 3.6206

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
76
Use a calculator to evaluate the logarithm.
-
A) -2.5320
B) -1.0942
C) -1.0996
D) -1.1051
-
A) -2.5320
B) -1.0942
C) -1.0996
D) -1.1051

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
77
Use a calculator to evaluate the logarithm.
-
A) -5.3882
B) -2.3497
C) -2.3307
D) -2.3401
-
A) -5.3882
B) -2.3497
C) -2.3307
D) -2.3401

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
78
Use a calculator to evaluate the logarithm.
-
A) 1.9823
B) 4.5643
C) 35.4244
D) 0.2184
-
A) 1.9823
B) 4.5643
C) 35.4244
D) 0.2184

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
79
Use a calculator to evaluate the logarithm.
-
A) 0.0192
B) -0.0083
C) 0.0083
D) -0.0192
-
A) 0.0192
B) -0.0083
C) 0.0083
D) -0.0192

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck
80
Write the expression as the logarithm of a single number or expression with a coefficient of 1. Assume all variables represent positive numbers.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 192 flashcards in this deck.
Unlock Deck
k this deck


