Deck 7: Linear Programming
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/203
Play
Full screen (f)
Deck 7: Linear Programming
1
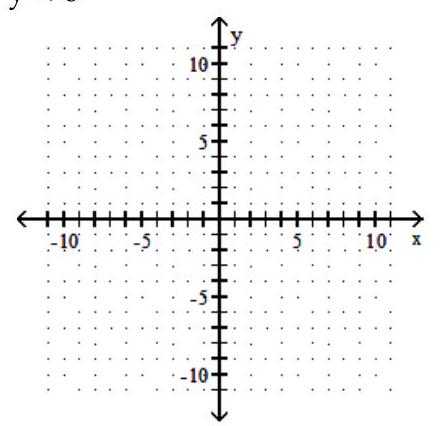
Graph the linear inequality.
-
A)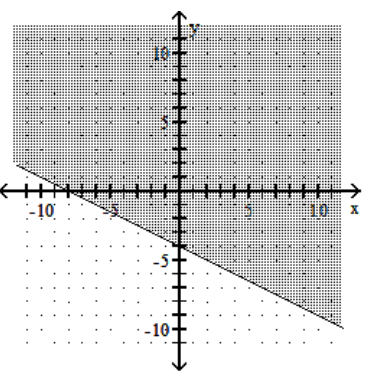
B)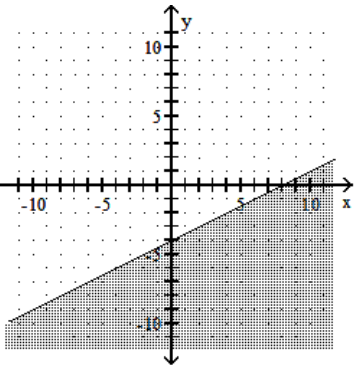
C)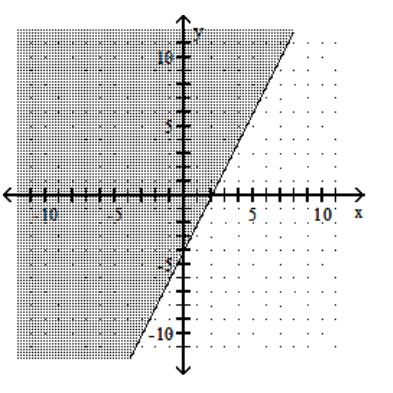
D)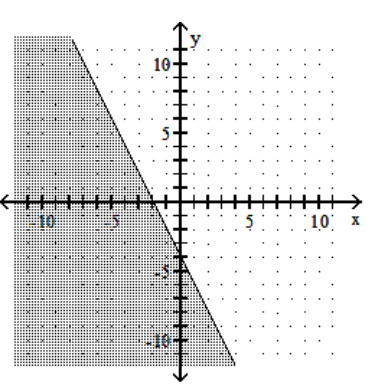
-

A)

B)

C)

D)


2
Graph the linear inequality.
-
A)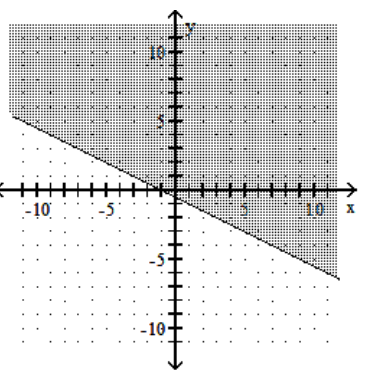
B)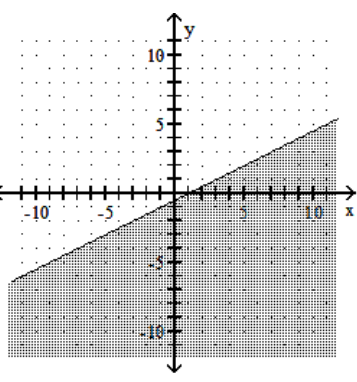
C)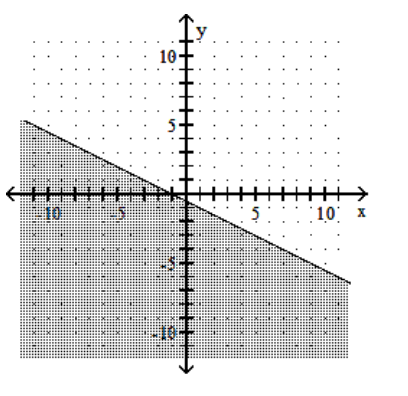
D)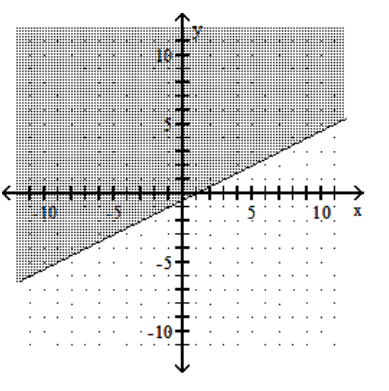
-

A)

B)

C)

D)


3
Graph the linear inequality.
-
A)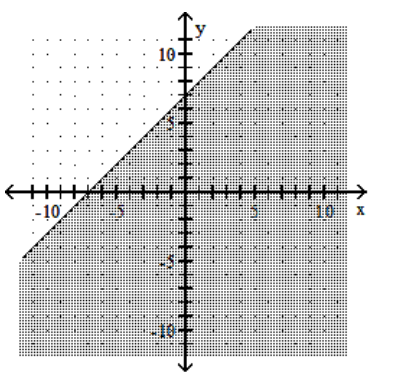
B)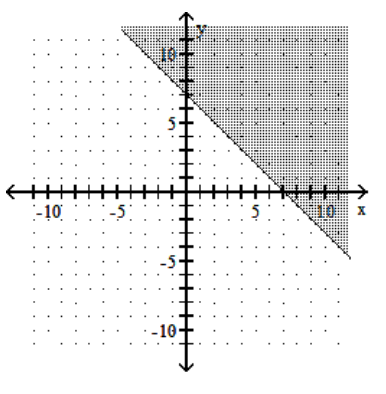
C)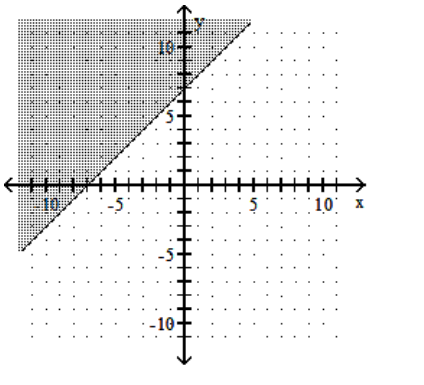
D)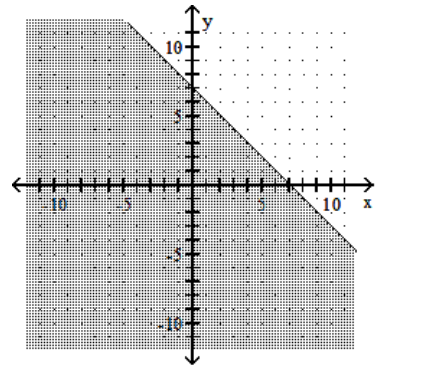
-

A)

B)

C)

D)


4
Graph the linear inequality.
-
A)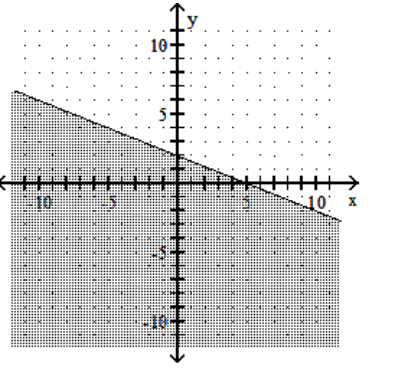
B)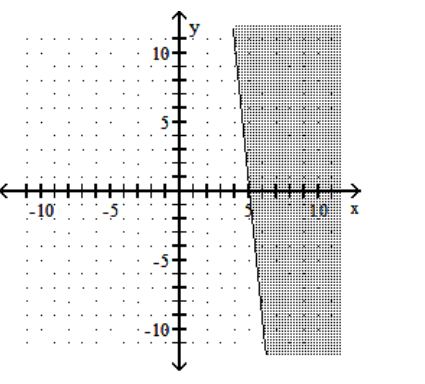
C)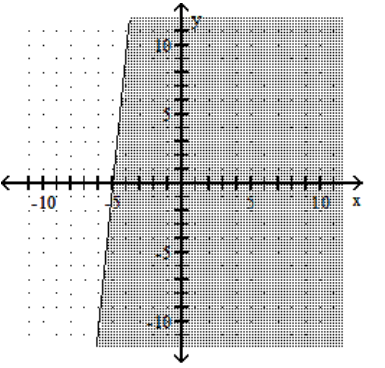
D)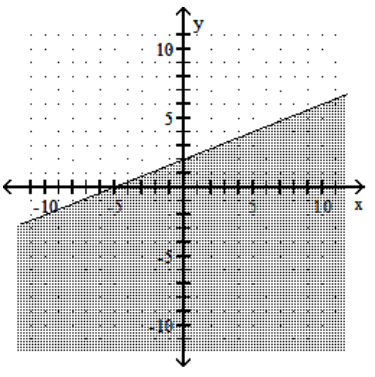
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
5
Graph the linear inequality.
-
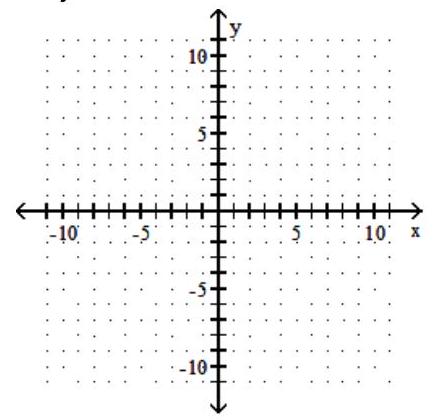
A)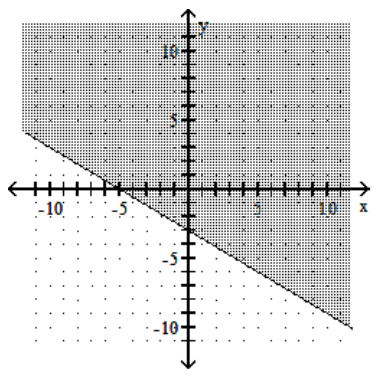
B)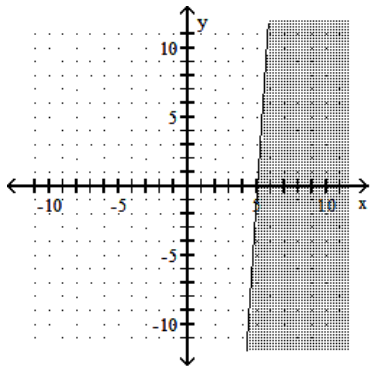
C)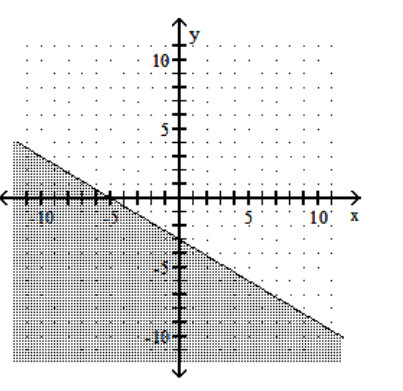
D)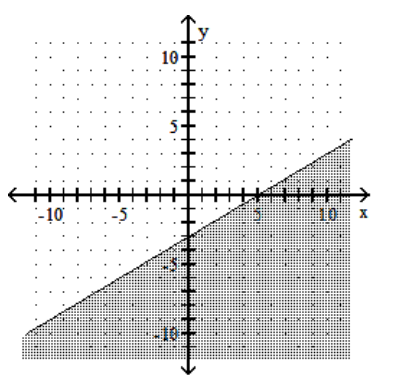
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
6
Graph the linear inequality.
-
A)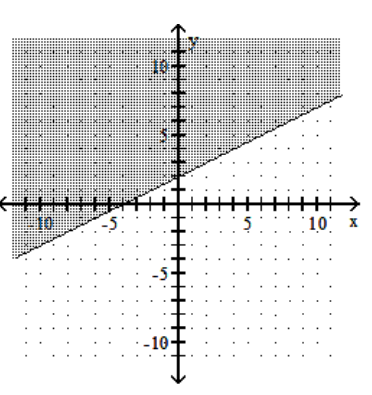
B)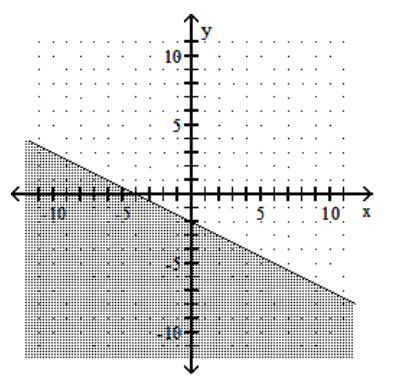
C)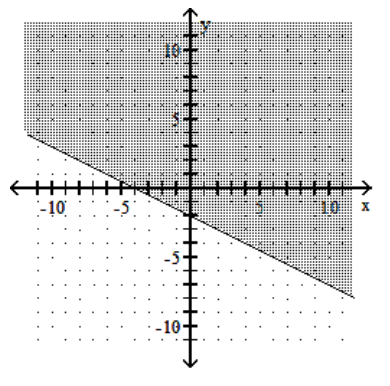
D)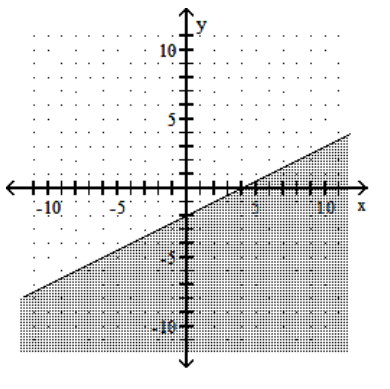
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
7
Graph the linear inequality.
-
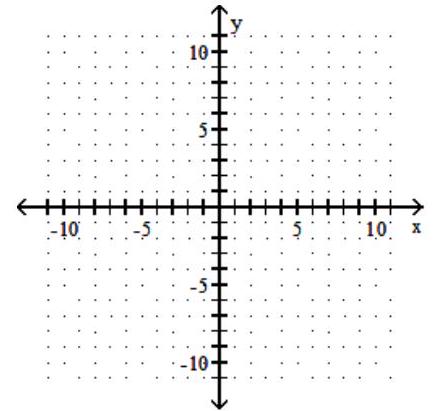
A)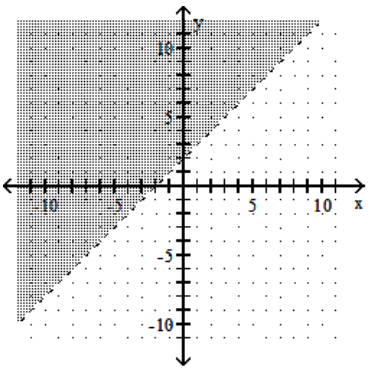
B)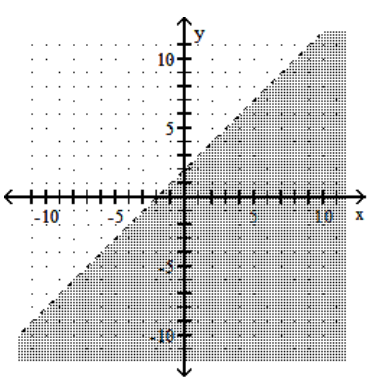
C)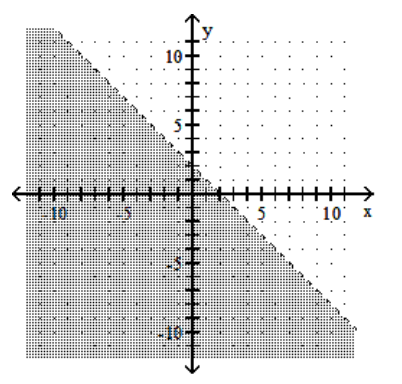
D)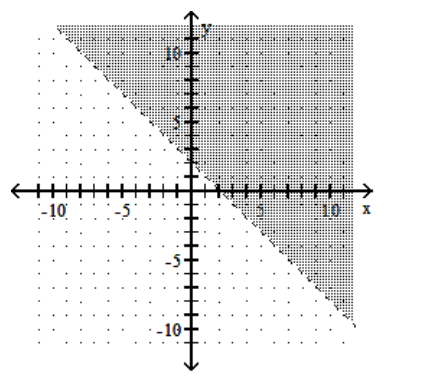
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
8
Graph the linear inequality.
-
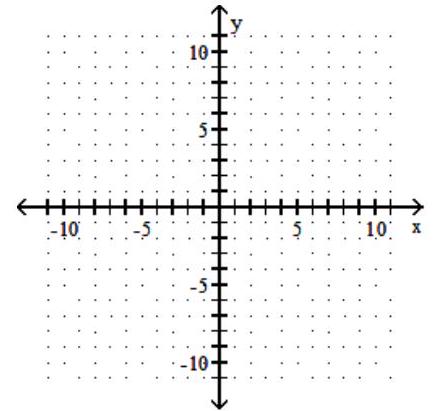
A)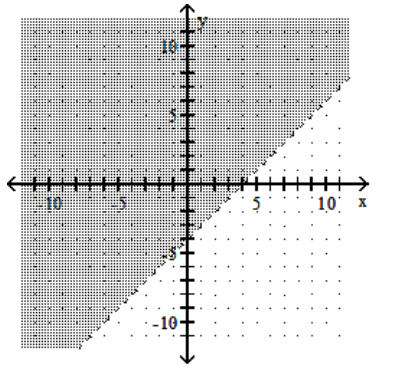
B)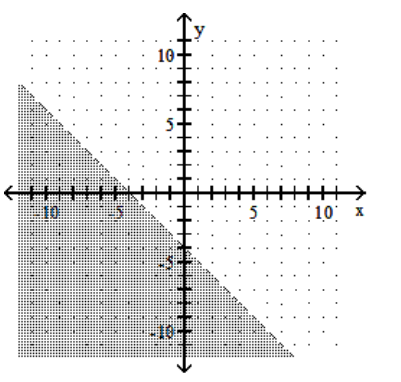
C)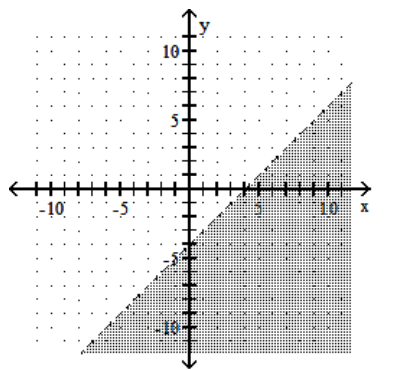
D)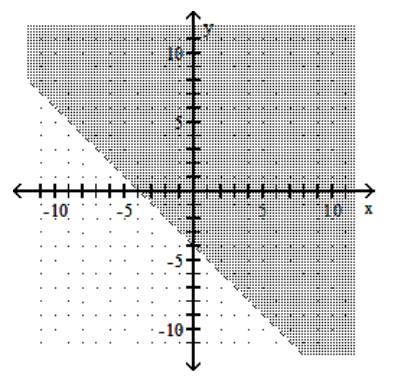
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
9
Graph the linear inequality.
-
A)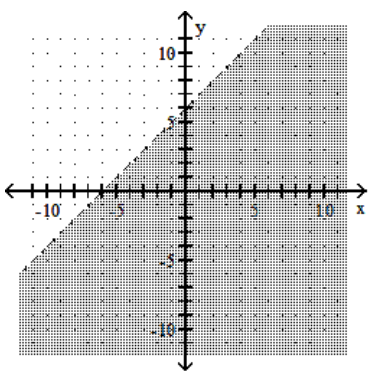
B)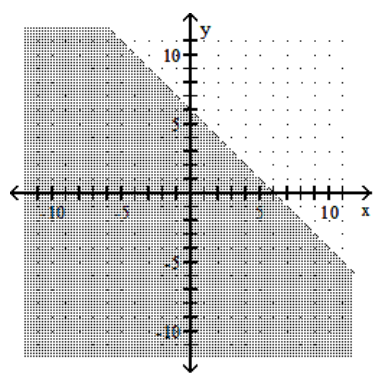
C)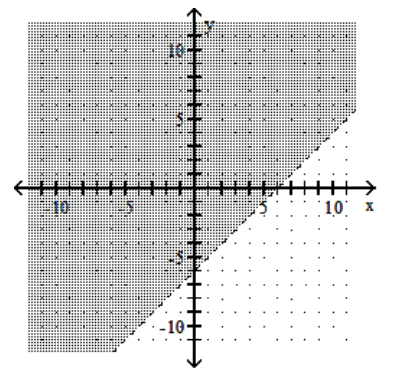
D)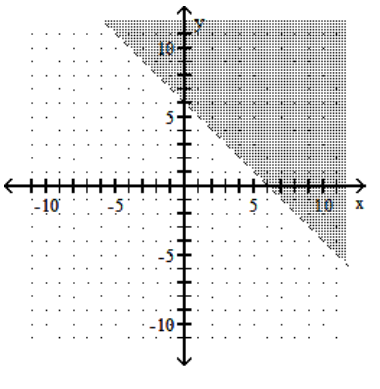
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
10
Graph the linear inequality.
-
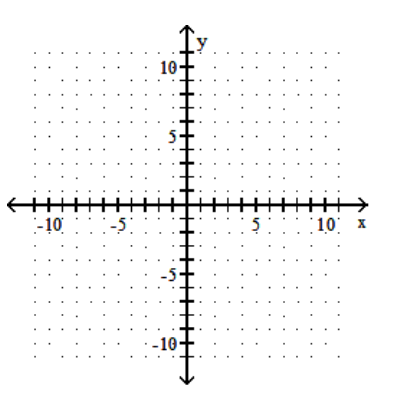
A)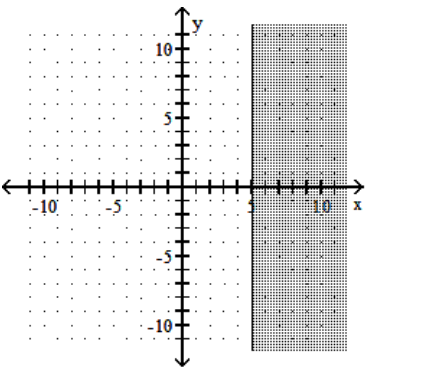
B)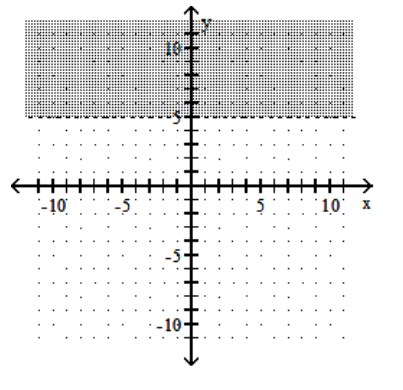
C)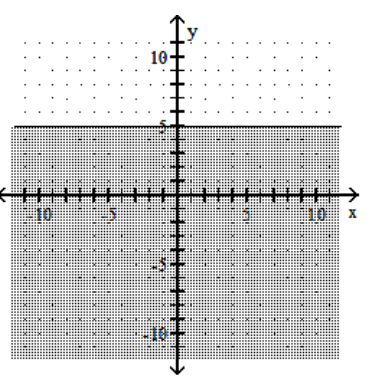
D)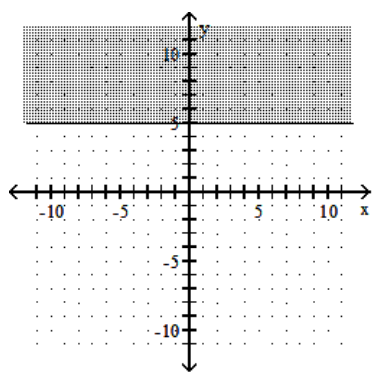
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
11
Graph the feasible region for the system of inequalities.
-
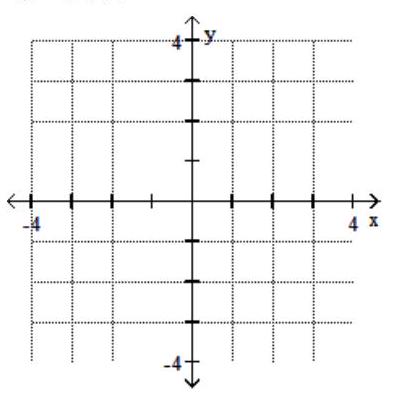
A)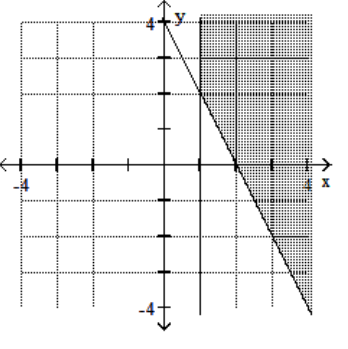
B)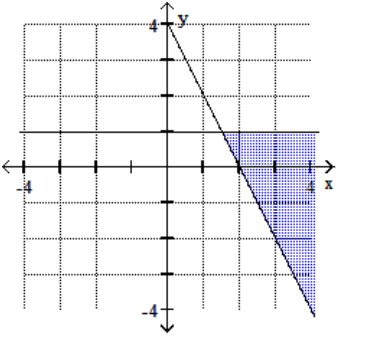
C)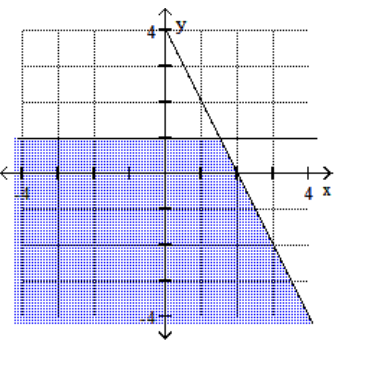
D)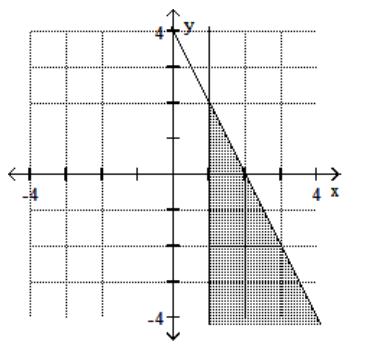
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
12
Graph the feasible region for the system of inequalities.
-
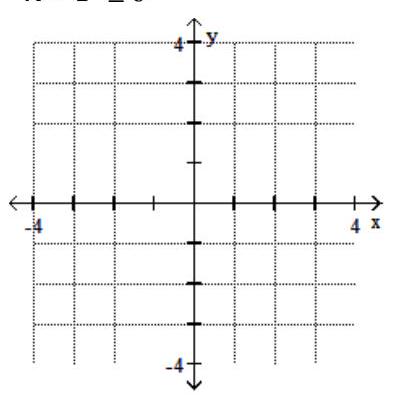
A)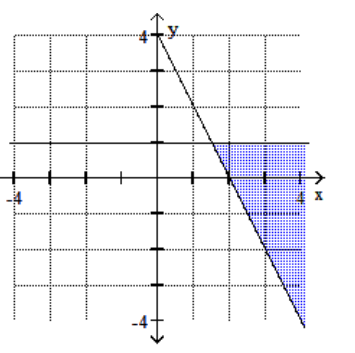
B)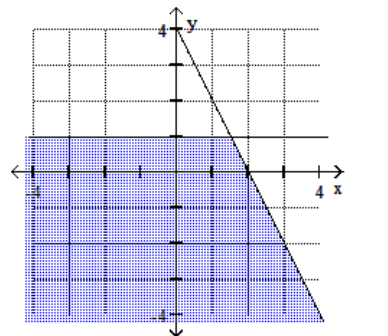
C)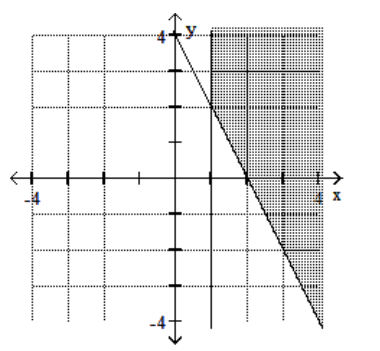
D)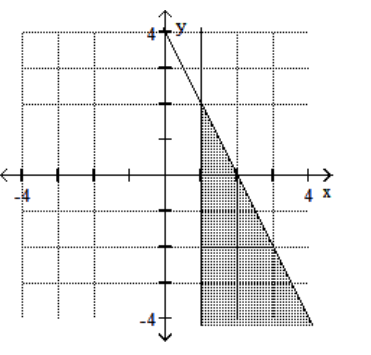
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
13
Graph the feasible region for the system of inequalities.
-
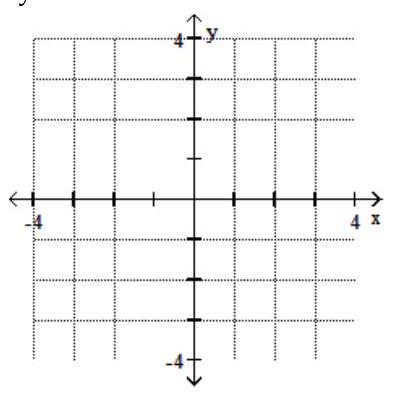
A)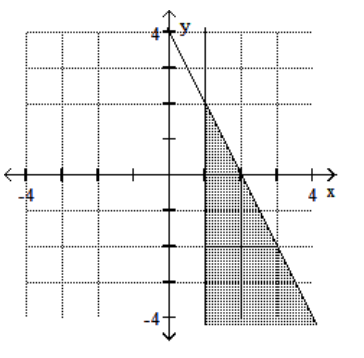
B)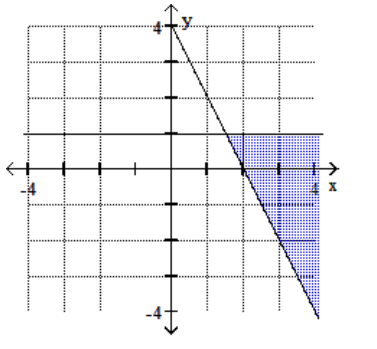
C)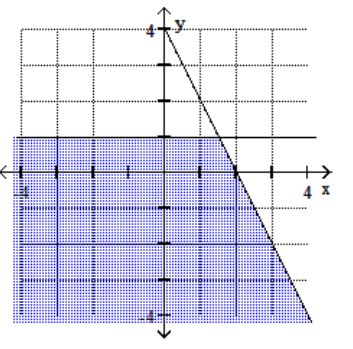
D)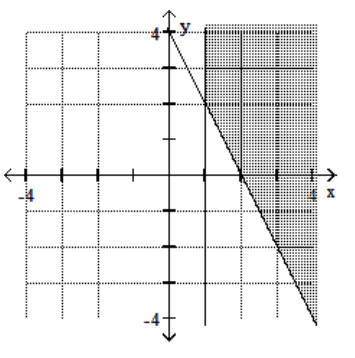
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
14
Graph the feasible region for the system of inequalities.
-
A)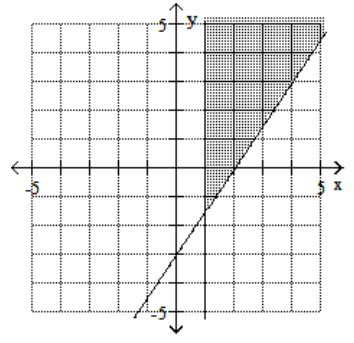
B)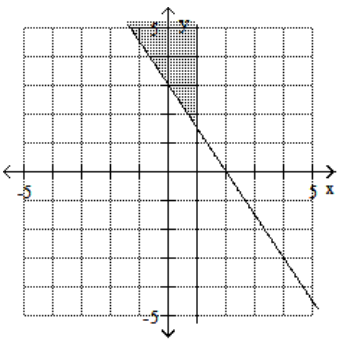
C)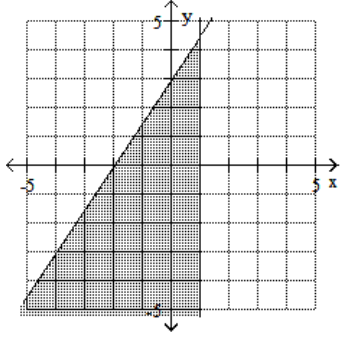
D)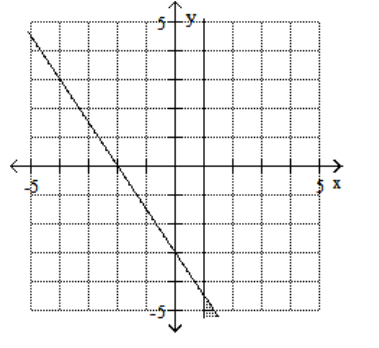
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
15
Graph the feasible region for the system of inequalities.
-
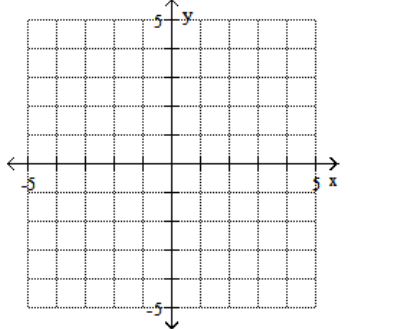
A)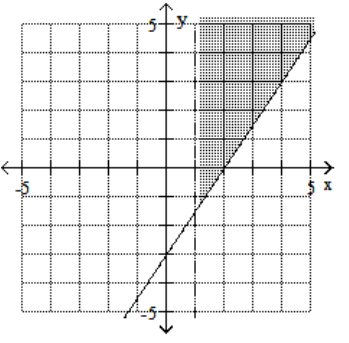
B)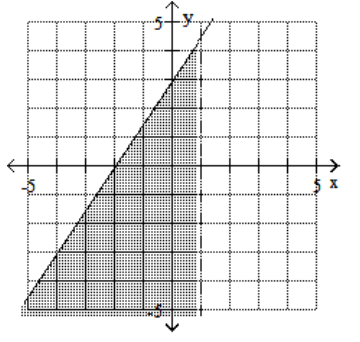
C)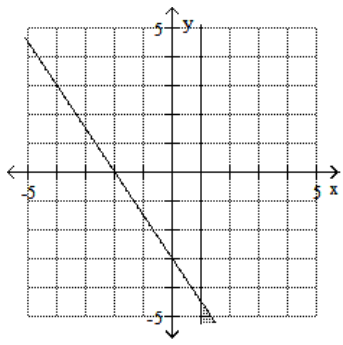
D)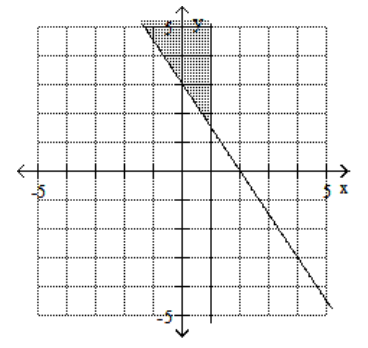
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
16
Graph the feasible region for the system of inequalities.
-
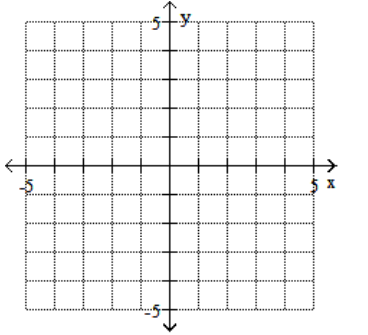
A)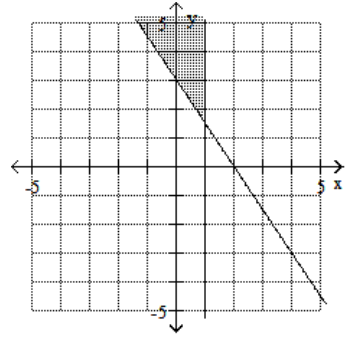
B)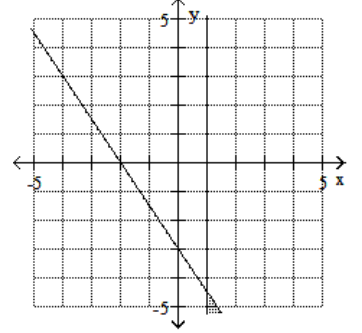
C)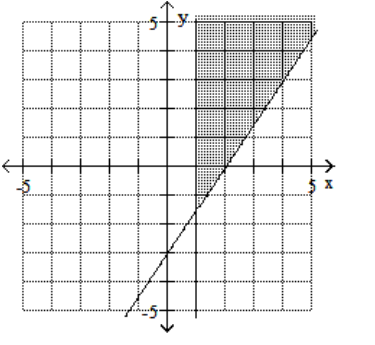
D)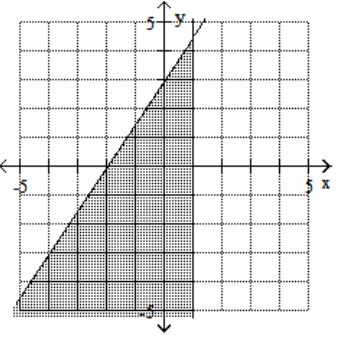
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
17
Graph the feasible region for the system of inequalities.
-
A)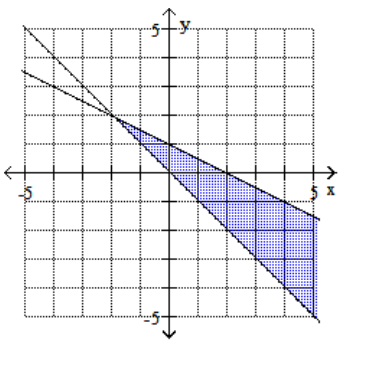
B)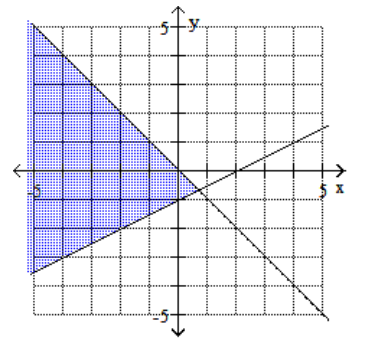
C)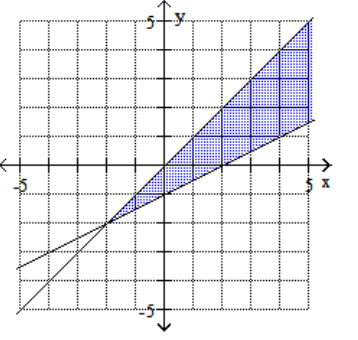
D)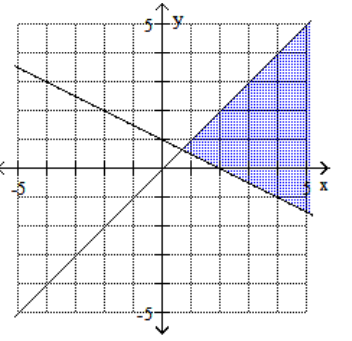
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
18
Graph the feasible region for the system of inequalities.
-
A)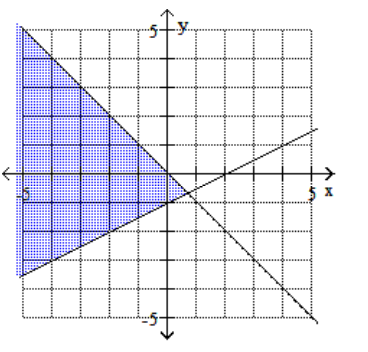
B)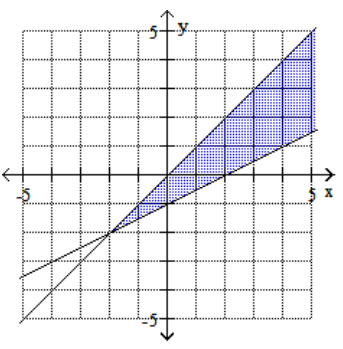
C)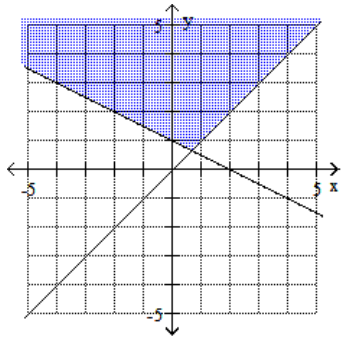
D)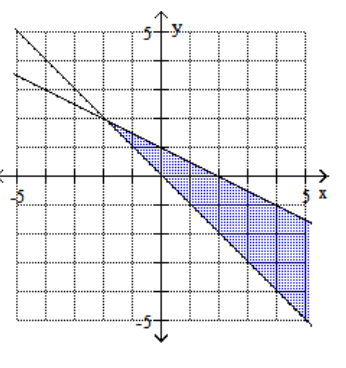
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
19
Graph the feasible region for the system of inequalities.
-
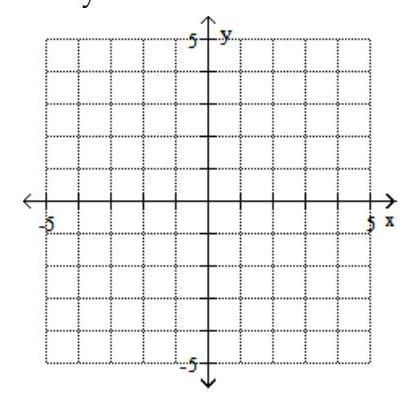
A)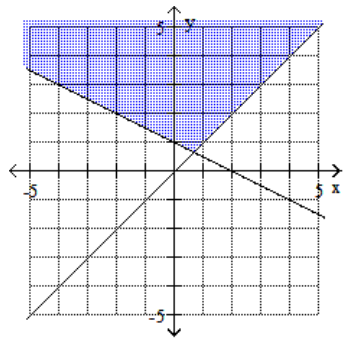
B)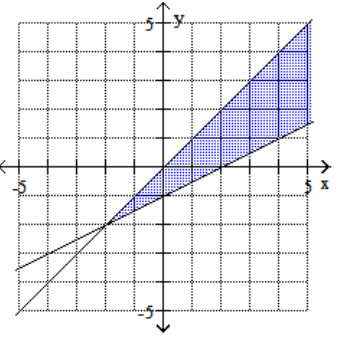
C)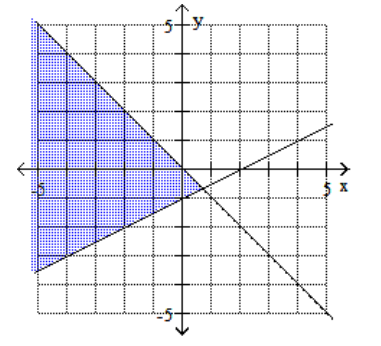
D)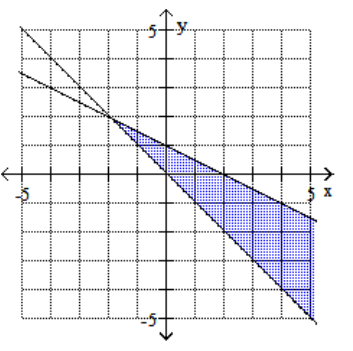
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
20
Graph the feasible region for the system of inequalities.
-
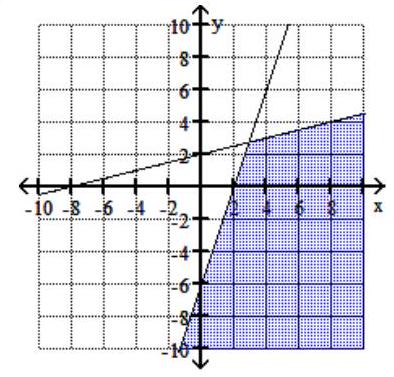
A)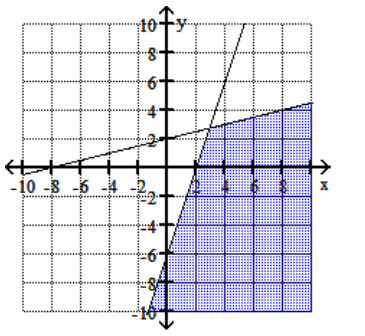
B)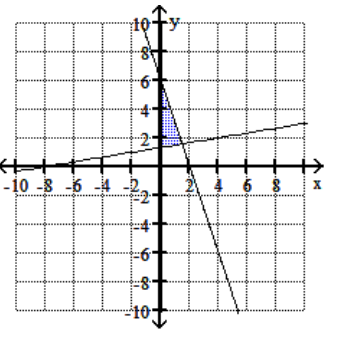
C)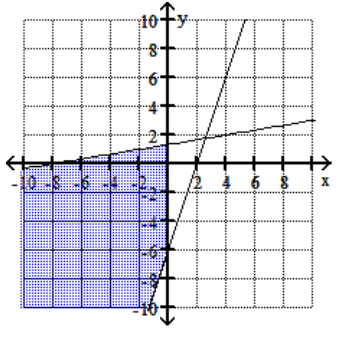
D)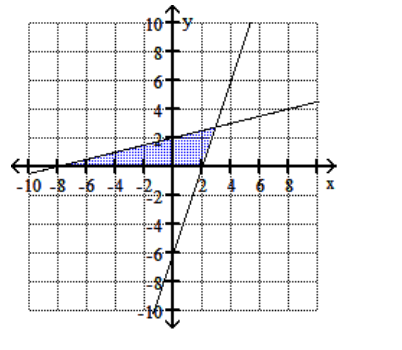
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
21
Graph the feasible region for the system of inequalities.
-
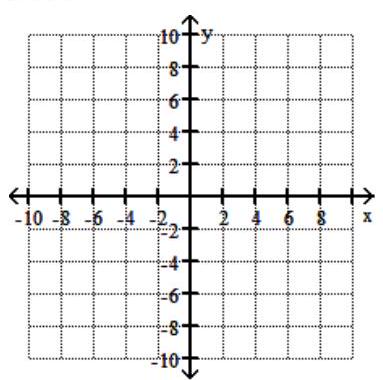
A)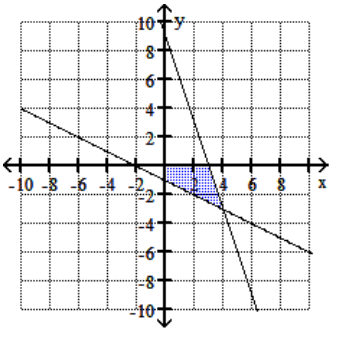
B)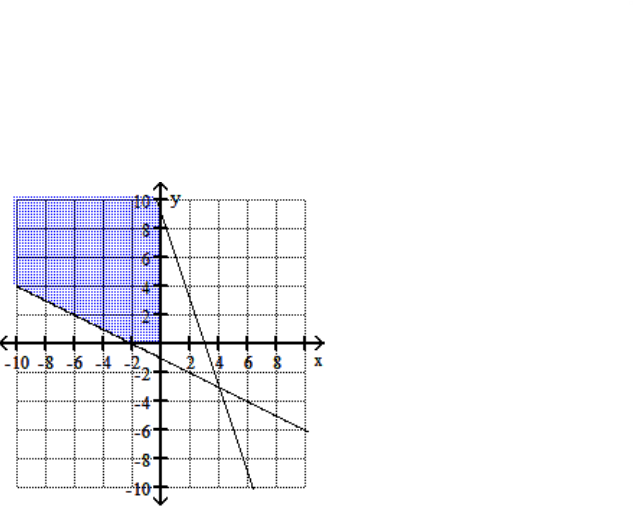
C)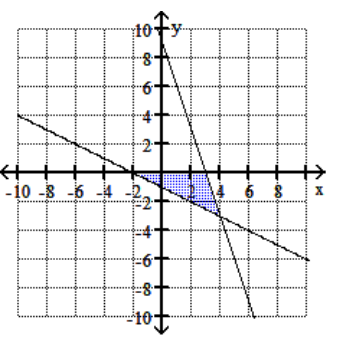
D)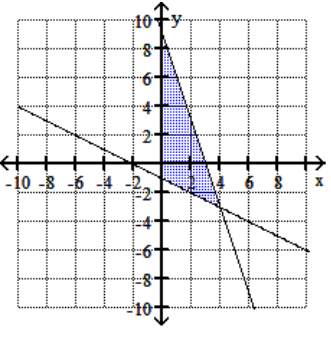
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
22
Graph the feasible region for the system of inequalities.
-
A)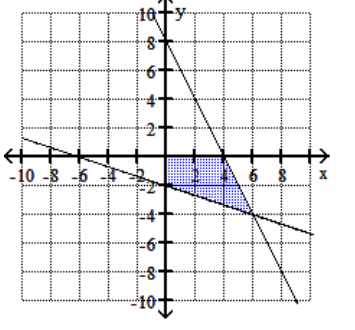
B)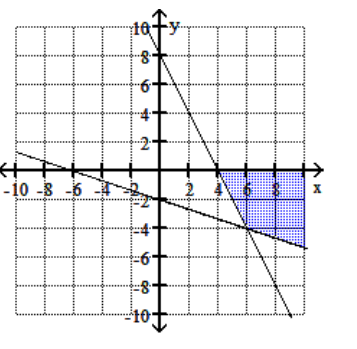
C)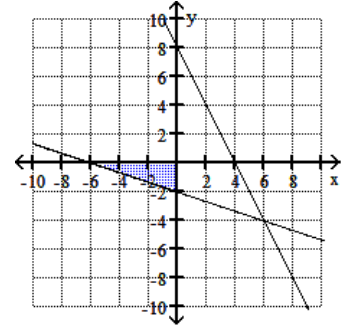
D)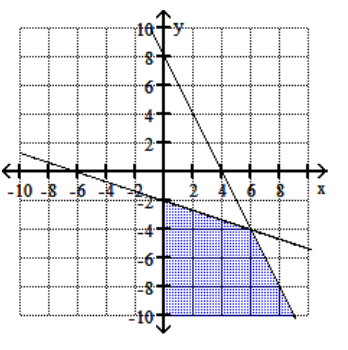
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
23
Graph the feasible region for the system of inequalities.
-
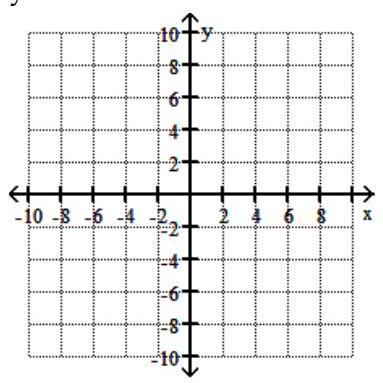
A)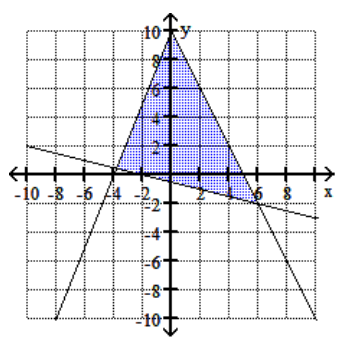
B)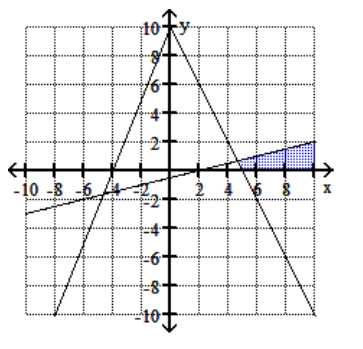
C)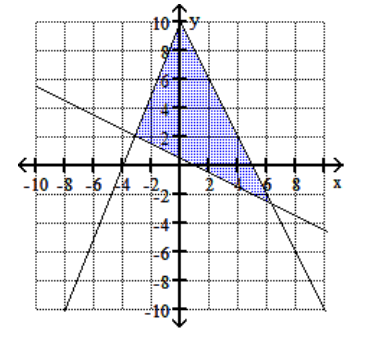
D)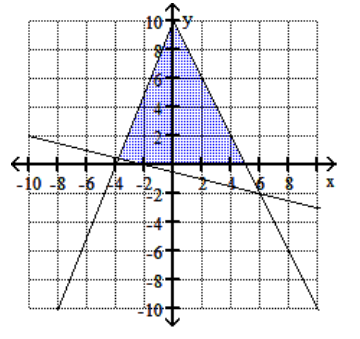
-

A)

B)

C)

D)


Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
24
A manufacturer of wooden chairs and tables must decide in advance how many of each item will be made in a givenweek. Use the table to find the system of inequalities that describes the manufacturer's weekly production.
-Use -for the number of chairs and for the number of tables made per week. The number of work hours a yailable for construction and finishing is fixed.
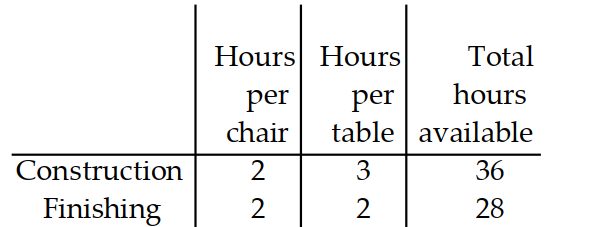
A)
B)
C)
D)
-Use -for the number of chairs and for the number of tables made per week. The number of work hours a yailable for construction and finishing is fixed.

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
25
A manufacturer of wooden chairs and tables must decide in advance how many of each item will be made in a givenweek. Use the table to find the system of inequalities that describes the manufacturer's weekly production.
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.
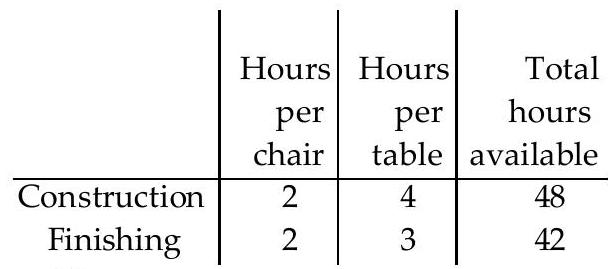
A)
B)
C)
D)
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
26
A manufacturer of wooden chairs and tables must decide in advance how many of each item will be made in a givenweek. Use the table to find the system of inequalities that describes the manufacturer's weekly production.
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.
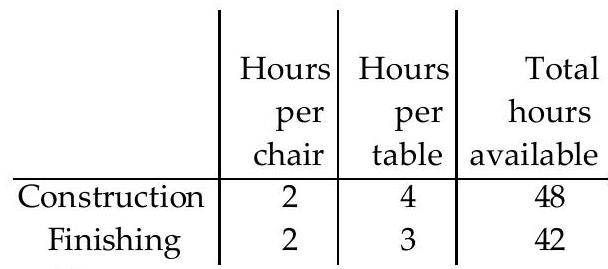
A)
B)
C)
D)
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
27
A manufacturer of wooden chairs and tables must decide in advance how many of each item will be made in a givenweek. Use the table to find the system of inequalities that describes the manufacturer's weekly production.
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.
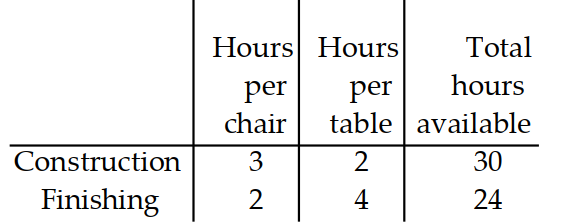
A)
B)
C)
D)
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
28
A manufacturer of wooden chairs and tables must decide in advance how many of each item will be made in a givenweek. Use the table to find the system of inequalities that describes the manufacturer's weekly production.
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.
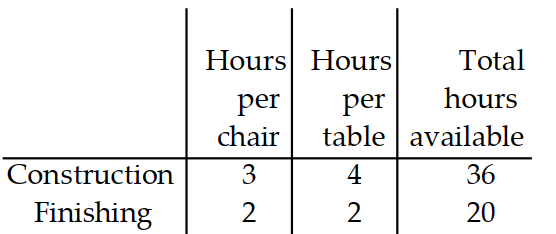
A)
B)
C)
D)
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
29
A manufacturer of wooden chairs and tables must decide in advance how many of each item will be made in a givenweek. Use the table to find the system of inequalities that describes the manufacturer's weekly production.
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.
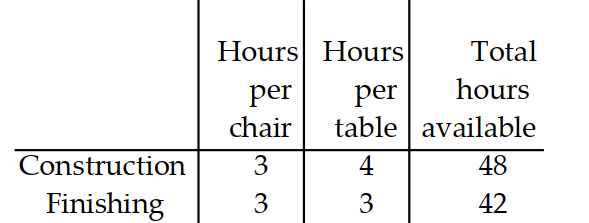
A)
B)
C)
D)
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
30
A manufacturer of wooden chairs and tables must decide in advance how many of each item will be made in a givenweek. Use the table to find the system of inequalities that describes the manufacturer's weekly production.
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.
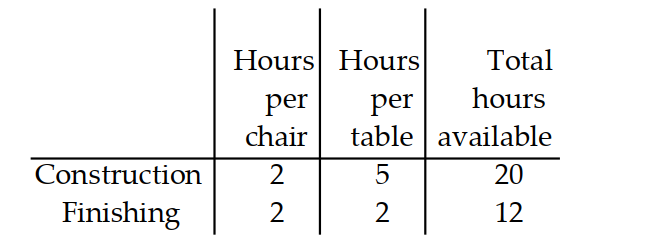
A)
B)
C)
D)
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.
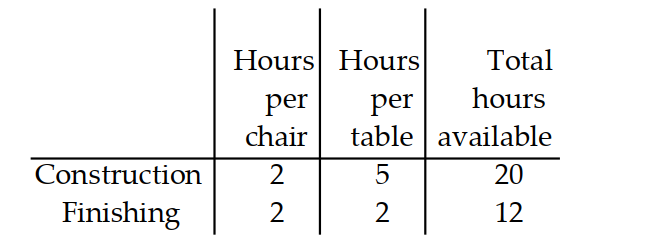
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
31
A manufacturer of wooden chairs and tables must decide in advance how many of each item will be made in a givenweek. Use the table to find the system of inequalities that describes the manufacturer's weekly production.
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.
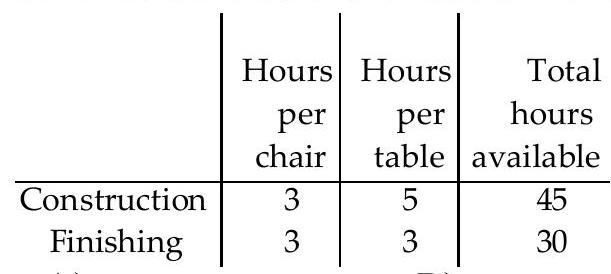
A)
B)
C)
D)
-Use for the number of chairs and for the number of tables made per week. The number of work-hours available for construction and finishing is fixed.

A)
B)
C)
D)

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
32
Find the value(s) of the function on the given feasible region.
-Find the maximum and minimum of .
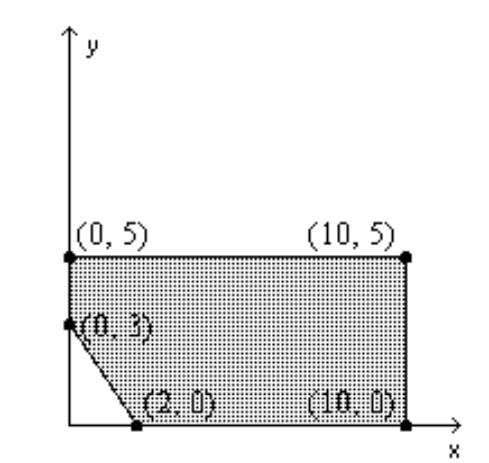
A) 225,15
B) 225,200
C) 200,15
D) 25,15
-Find the maximum and minimum of .

A) 225,15
B) 225,200
C) 200,15
D) 25,15

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
33
Find the value(s) of the function on the given feasible region.
-Find the minimum of .
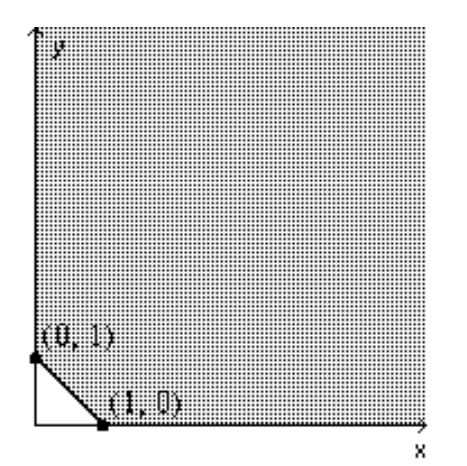
A) 42
B) 56
C) 19
D) 33
-Find the minimum of .

A) 42
B) 56
C) 19
D) 33

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
34
Find the value(s) of the function on the given feasible region.
-Find the maximum and minimum of .
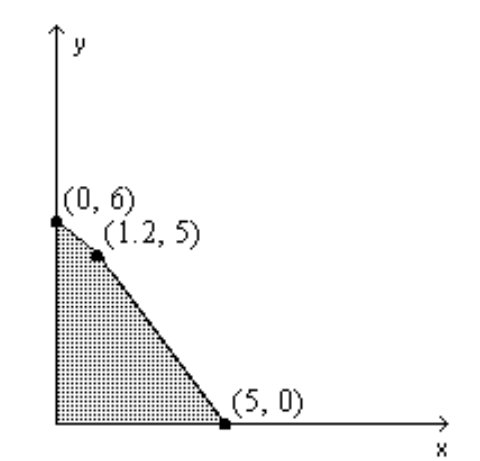
A)
B)
C)
D) 40,0
-Find the maximum and minimum of .

A)
B)
C)
D) 40,0

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
35
Find the value(s) of the function on the given feasible region.
-Find the maximum and minimum of .
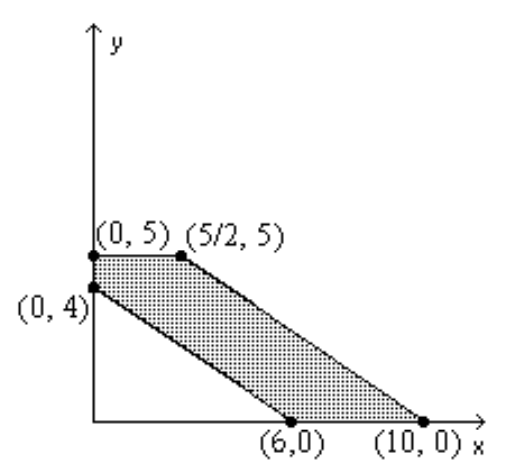
A) 36,30
B)
C) 42,24
D) 60,24
-Find the maximum and minimum of .

A) 36,30
B)
C) 42,24
D) 60,24

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
36
Find the value(s) of the function on the given feasible region.
-Find the minimum of .
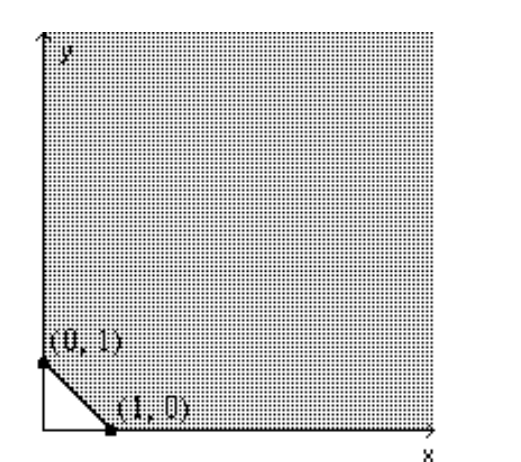
A) 29
B) 39
C) 15
D) 10
-Find the minimum of .

A) 29
B) 39
C) 15
D) 10

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
37
Use graphical methods to solve the linear programming problem.
-Maximize
Subject to:
A) Maximum of 52 when and
B) Maximum of 32 when and
C) Maximum of 24 when and
D) Maximum of 32 when and
-Maximize
Subject to:

A) Maximum of 52 when and
B) Maximum of 32 when and
C) Maximum of 24 when and
D) Maximum of 32 when and

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
38
Use graphical methods to solve the linear programming problem.
-Maximize
Subject to:
A) Maximum of 120 when and
B) Maximum of 92 when and
C) Maximum of 96 when and
D) Maximum of 100 when and
-Maximize
Subject to:

A) Maximum of 120 when and
B) Maximum of 92 when and
C) Maximum of 96 when and
D) Maximum of 100 when and

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
39
Use graphical methods to solve the linear programming problem.
-Minimize
Subject to:
A) Minimum of 1.08 when and
B) Minimum of 1.86 when and
C) Minimum of 1.2 when and
D) Minimum of 1.02 when and
-Minimize
Subject to:

A) Minimum of 1.08 when and
B) Minimum of 1.86 when and
C) Minimum of 1.2 when and
D) Minimum of 1.02 when and

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
40
Use graphical methods to solve the linear programming problem.
-Maximize
Subject to:
A) Maximum of when and
B) Maximum of 19 when and
C) Maximum of 10 when and
D) Maximum of when and
-Maximize
Subject to:

A) Maximum of when and
B) Maximum of 19 when and
C) Maximum of 10 when and
D) Maximum of when and

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
41
Use graphical methods to solve the linear programming problem.
-Minimize
Subject to:
A) Minimum of 20 when and
B) Minimum of 20 when and
C) Minimum of 20 when and , as well as when and , and all points in between
D) Minimum of 0 when and
-Minimize
Subject to:

A) Minimum of 20 when and
B) Minimum of 20 when and
C) Minimum of 20 when and , as well as when and , and all points in between
D) Minimum of 0 when and

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
42
Use graphical methods to solve the linear programming problem.
-Minimize
Subject to:
A) Minimum of 26 when and
B) Minimum of 36 when and
C) Minimum of when and
D) Minimum of 0 when and
-Minimize
Subject to:

A) Minimum of 26 when and
B) Minimum of 36 when and
C) Minimum of when and
D) Minimum of 0 when and

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
43
Use graphical methods to solve the linear programming problem.
-Minimize
Subject to:
A) Minimum of 33 when and
B) Minimum of 39 when and
C) Minimum of 20 when and
D) Minimum of 75 when and
-Minimize
Subject to:

A) Minimum of 33 when and
B) Minimum of 39 when and
C) Minimum of 20 when and
D) Minimum of 75 when and

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
44
Find the value(s) of the function, subject to the system of inequalities.
-Find the maximum and minimum of subject to:
.
A) 345,63
B) 105,63
C) 240,63
D) 345,240
-Find the maximum and minimum of subject to:
.
A) 345,63
B) 105,63
C) 240,63
D) 345,240

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
45
Find the value(s) of the function, subject to the system of inequalities.
-Find the minimum of subject to:
.
A) 46
B) 39
C) 30
D) 23
-Find the minimum of subject to:
.
A) 46
B) 39
C) 30
D) 23

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
46
Find the value(s) of the function, subject to the system of inequalities.
-Find the maximum and minimum of subject to:
, and .
A)
B) 45,0
C)
D)
-Find the maximum and minimum of subject to:
, and .
A)
B) 45,0
C)
D)

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
47
Find the value(s) of the function, subject to the system of inequalities.
-Find the maximum and minimum of subject to:
.
A) 190,36
B) 60,36
C) 250,190
D) 250,36
-Find the maximum and minimum of subject to:
.
A) 190,36
B) 60,36
C) 250,190
D) 250,36

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
48
Find the value(s) of the function, subject to the system of inequalities.
-Find the minimum of subject to:
.
A) 35
B) 50
C) 34
D) 19
-Find the minimum of subject to:
.
A) 35
B) 50
C) 34
D) 19

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
49
Find the value(s) of the function, subject to the system of inequalities.
-Find the maximum and minimum of subject to:
, and .
A) 45,0
B)
C)
D)
-Find the maximum and minimum of subject to:
, and .
A) 45,0
B)
C)
D)

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
50
State the linear programming problem in mathematical terms, identifying the objective function and the constraints.
-A firm makes products and B. Product A takes 3 hours each on machine and machine M; product B takes 3 hours on and 2 hours on M. Machine can be used for 13 hours and M for 8 hours. Profit on product is and on B. Maximize profit.
A) Maximize
Subject to:
.
B) Maximize
Subject to:
.
C) Maximize
Subject to:
.
D) Maximize
Subject to:
.
-A firm makes products and B. Product A takes 3 hours each on machine and machine M; product B takes 3 hours on and 2 hours on M. Machine can be used for 13 hours and M for 8 hours. Profit on product is and on B. Maximize profit.
A) Maximize
Subject to:
.
B) Maximize
Subject to:
.
C) Maximize
Subject to:
.
D) Maximize
Subject to:
.

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
51
State the linear programming problem in mathematical terms, identifying the objective function and the constraints.
-A car repair shop blends oil from two suppliers. Supplier I can supply at most 45 gal with detergent. Supplier II can supply at most with detergent. How much can be ordered from each to get at most 100 gal of oil with maximum detergent?
A) Maximize
Subject to:
.
B) Maximize
Subject to:
.
C) Maximize
Subject to:
.
D) Maximize
Subject to:
.
-A car repair shop blends oil from two suppliers. Supplier I can supply at most 45 gal with detergent. Supplier II can supply at most with detergent. How much can be ordered from each to get at most 100 gal of oil with maximum detergent?
A) Maximize
Subject to:
.
B) Maximize
Subject to:
.
C) Maximize
Subject to:
.
D) Maximize
Subject to:
.

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
52
State the linear programming problem in mathematical terms, identifying the objective function and the constraints.
-A breed of cattle needs at least 10 protein and 8 fat units per day. Feed type I provides 6 protein and 2 fat units at . Feed ty pe II provides 2 protein and 5 fat units at . Which mixture fills the needs at minimum cost?
A) Minimize
Subject to:
.
B) Minimize
Subject to:
.
C) Minimize
Subject to:
.
D) Minimize
Subject to:
.
-A breed of cattle needs at least 10 protein and 8 fat units per day. Feed type I provides 6 protein and 2 fat units at . Feed ty pe II provides 2 protein and 5 fat units at . Which mixture fills the needs at minimum cost?
A) Minimize
Subject to:
.
B) Minimize
Subject to:
.
C) Minimize
Subject to:
.
D) Minimize
Subject to:
.

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
53
The Acme Class Ring Company designs and sells two types of rings: the VIP and the SST. They can produce up to 24rings each day using up to 60 total man hours of labor. It takes 3 man hours to make one VIP ring, versus 2 man hoursto make one SST ring.
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
A) 12 VIP and 12 SST
B) 8 VIP and 16 SST
C)0 VIP and 24 SST
D) 16 VIP and 8 SST
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
A) 12 VIP and 12 SST
B) 8 VIP and 16 SST
C)0 VIP and 24 SST
D) 16 VIP and 8 SST

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
54
The Acme Class Ring Company designs and sells two types of rings: the VIP and the SST. They can produce up to 24rings each day using up to 60 total man hours of labor. It takes 3 man hours to make one VIP ring, versus 2 man hoursto make one SST ring.
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
A) 16 VIP and 8 SST
B) 8 VIP and 16 SST
C) 0 VIP and 24 SST
D) 12 VIP and 12 SST
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
A) 16 VIP and 8 SST
B) 8 VIP and 16 SST
C) 0 VIP and 24 SST
D) 12 VIP and 12 SST

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
55
The Acme Class Ring Company designs and sells two types of rings: the VIP and the SST. They can produce up to 24rings each day using up to 60 total man hours of labor. It takes 3 man hours to make one VIP ring, versus 2 man hoursto make one SST ring.
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
A) 20 VIP and 4 SST
B) and 4 SST
C) 24 VIP and 0 SST
D) 20 VIP and 0 SST
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
A) 20 VIP and 4 SST
B) and 4 SST
C) 24 VIP and 0 SST
D) 20 VIP and 0 SST

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
56
The Acme Class Ring Company designs and sells two types of rings: the VIP and the SST. They can produce up to 24rings each day using up to 60 total man hours of labor. It takes 3 man hours to make one VIP ring, versus 2 man hoursto make one SST ring.
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
A) 16 VIP and 8 SST
B) 18 VIP and 6 SST
C) 12 VIP and 12 SST
D) 14 VIP and 10 SST
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
A) 16 VIP and 8 SST
B) 18 VIP and 6 SST
C) 12 VIP and 12 SST
D) 14 VIP and 10 SST

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
57
The Acme Class Ring Company designs and sells two types of rings: the VIP and the SST. They can produce up to 24rings each day using up to 60 total man hours of labor. It takes 3 man hours to make one VIP ring, versus 2 man hoursto make one SST ring.
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
A) 12 VIP and 12 SST
B) 10 VIP and 14 SST
C) 14 VIP and 14 SST
D) 14 VIP and 10 SST
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
A) 12 VIP and 12 SST
B) 10 VIP and 14 SST
C) 14 VIP and 14 SST
D) 14 VIP and 10 SST

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
58
The Acme Class Ring Company designs and sells two types of rings: the VIP and the SST. They can produce up to 24rings each day using up to 60 total man hours of labor. It takes 3 man hours to make one VIP ring, versus 2 man hoursto make one SST ring.
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
A) 24 VIP and 4 SST
B) 20 VIP and 4 SST
C) 24 VIP and 0 SST
D) 20 VIP and 0 SST
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
A) 24 VIP and 4 SST
B) 20 VIP and 4 SST
C) 24 VIP and 0 SST
D) 20 VIP and 0 SST

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
59
The Acme Class Ring Company designs and sells two types of rings: the VIP and the SST. They can produce up to 24rings each day using up to 60 total man hours of labor. It takes 3 man hours to make one VIP ring, versus 2 man hoursto make one SST ring.
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
A) 12 VIP and 12 SST
B) 0 VIP and 20 SST
C) 4 VIP and 20 SST
D) 0 VIP and 24 SST
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
A) 12 VIP and 12 SST
B) 0 VIP and 20 SST
C) 4 VIP and 20 SST
D) 0 VIP and 24 SST

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
60
The Acme Class Ring Company designs and sells two types of rings: the VIP and the SST. They can produce up to 24rings each day using up to 60 total man hours of labor. It takes 3 man hours to make one VIP ring, versus 2 man hoursto make one SST ring.
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
A) 12 VIP and 12 SST
B) 14 VIP and 10 SST
C) 20 VIP and 4 SST
D) 10 VIP and 14 SST
-How many of each type of ring should be made daily to maximize the company's profit, if the profit on a VIP ring is and on an SST ring is ?
A) 12 VIP and 12 SST
B) 14 VIP and 10 SST
C) 20 VIP and 4 SST
D) 10 VIP and 14 SST

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
61
Provide an appropriate response.
-To determine the shading when graphing , the point would make a good test point. ?
-To determine the shading when graphing , the point would make a good test point. ?

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
62
Provide an appropriate response.
-The graph of is always shaded above the line , regardless of any nonzero choices of , and .
-The graph of is always shaded above the line , regardless of any nonzero choices of , and .

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
63
Provide an appropriate response.
-The feasible region of a set of two inequalities must always be unbounded.
-The feasible region of a set of two inequalities must always be unbounded.

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
64
Provide an appropriate response.
-It is possible to have a system of linear inequalities with a feasible region that includes more than one enclosed region.
-It is possible to have a system of linear inequalities with a feasible region that includes more than one enclosed region.

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
65
Provide an appropriate response.
-If a system has four inequalities, the number of corner points of the feasible region must be ?
A) exactly three
B) at least three, but not more than four
C) at least one, but not more than four
D) exactly four
-If a system has four inequalities, the number of corner points of the feasible region must be ?
A) exactly three
B) at least three, but not more than four
C) at least one, but not more than four
D) exactly four

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
66
Provide an appropriate response.
-Describe the feasible region of and .
A) Two bounded regions
B) A bounded region
C) An empty region
D) An unbounded region
-Describe the feasible region of and .
A) Two bounded regions
B) A bounded region
C) An empty region
D) An unbounded region

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
67
Provide an appropriate response.
-Describe the feasible region of , and .
A) Two bounded regions
B) An empty region
C) A bounded region
D) An unbounded region
-Describe the feasible region of , and .
A) Two bounded regions
B) An empty region
C) A bounded region
D) An unbounded region

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
68
Provide an appropriate response.
-If the inequalities and are included in a system, the feasibility region is restricted to the axes and which quadrant?
A) Fourth
B) First
C) Second
D) It is not restricted.
-If the inequalities and are included in a system, the feasibility region is restricted to the axes and which quadrant?
A) Fourth
B) First
C) Second
D) It is not restricted.

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
69
Provide an appropriate response.
-If a system of inequalities includes , then the feasibility region is restricted to what?
A) The region right of and including
B) The region left of and including
C) The region left of and including
D) The region right of and including
-If a system of inequalities includes , then the feasibility region is restricted to what?
A) The region right of and including
B) The region left of and including
C) The region left of and including
D) The region right of and including

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
70
Provide an appropriate response.
-What is the least number of inequalities needed to produce a closed region?
A) 1
B) 2
C) 4
D) 3
-What is the least number of inequalities needed to produce a closed region?
A) 1
B) 2
C) 4
D) 3

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
71
Provide an appropriate response.
-Is it possible to have a bounded feasible region that does not optimize an objective function?
-Is it possible to have a bounded feasible region that does not optimize an objective function?

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
72
Provide an appropriate response.
-Is it possible that the feasible region of a linear program include more than one distinct area?
-Is it possible that the feasible region of a linear program include more than one distinct area?

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
73
Provide an appropriate response.
-Does a linear program with at least three constraints always have a closed feasible region?
-Does a linear program with at least three constraints always have a closed feasible region?

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
74
Provide an appropriate response.
-Consider a linear program with an objective function for profit. Thinking of isoprofit lines, if the objective function is evaluated at the corner points of polygon , and , and , is it safe to assume that is not the corner point at which the profit is maximized?
-Consider a linear program with an objective function for profit. Thinking of isoprofit lines, if the objective function is evaluated at the corner points of polygon , and , and , is it safe to assume that is not the corner point at which the profit is maximized?

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
75
Provide an appropriate response.
-A linear program is defined with constraints , and . Is the feasibility region bounded, unbounded, or empty?
A) Bounded
B) Unbounded
C) Empty
-A linear program is defined with constraints , and . Is the feasibility region bounded, unbounded, or empty?
A) Bounded
B) Unbounded
C) Empty

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
76
Write the word or phrase that best completes each statement or answers thequestion.
-Explain how you decide which half-plane to shade when you are graphing an inequality.
-Explain how you decide which half-plane to shade when you are graphing an inequality.

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
77
Write the word or phrase that best completes each statement or answers thequestion.
-Explain why the graphing method is not satisfactory for solving a linear programming problem with 3 variables.
-Explain why the graphing method is not satisfactory for solving a linear programming problem with 3 variables.

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
78
Write the word or phrase that best completes each statement or answers thequestion.
-Explain why the solution to a linear programming problem always occurs at a corner point of the feasible region.
-Explain why the solution to a linear programming problem always occurs at a corner point of the feasible region.

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
79
Write the word or phrase that best completes each statement or answers thequestion.
-Can there be more than one point in the feasible region where the maximum or minimum occurs? Explain.
-Can there be more than one point in the feasible region where the maximum or minimum occurs? Explain.

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck
80
Write the word or phrase that best completes each statement or answers thequestion.
-In an unbounded region, will there always be a solution?
-In an unbounded region, will there always be a solution?

Unlock Deck
Unlock for access to all 203 flashcards in this deck.
Unlock Deck
k this deck


