Deck 8: Sets and Probability
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/240
Play
Full screen (f)
Deck 8: Sets and Probability
1
Tell whether the statement is true or false.
-
-
False
2
Tell whether the statement is true or false.
-
-
False
3
Tell whether the statement is true or false.
- is an even counting number between 8 and 14
- is an even counting number between 8 and 14
False
4
Tell whether the statement is true or false.
-
-

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
5
Tell whether the statement is true or false.
-
-

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
6
Tell whether the statement is true or false.
- is an even counting number
- is an even counting number

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
7
Tell whether the statement is true or false.
- is a counting number greater than 34
- is a counting number greater than 34

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
8
Insert " " or "q" in the blank to make the statement true.
-
A)
B)
-
A)
B)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
9
Insert " " or "q" in the blank to make the statement true.
-
A)
B)
-
A)
B)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
10
Insert " " or "q" in the blank to make the statement true.
-
A)
B)
-
A)
B)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
11
Insert " " or "q" in the blank to make the statement true.
-
A)
B)
-
A)
B)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
12
Insert " " or "q" in the blank to make the statement true.
-{k, b, d} _{k, b, d}
A)
B)
-{k, b, d} _{k, b, d}
A)
B)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
13
Insert " " or "q" in the blank to make the statement true.
- is a counting number larger than 5
A)
B)
- is a counting number larger than 5
A)
B)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
14
Find the number of subsets of the set.
-{8, 9, 10}
A) 7
B) 3
C) 6
D) 8
-{8, 9, 10}
A) 7
B) 3
C) 6
D) 8

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
15
Find the number of subsets of the set.
-
A) 1
B) 4
C) 0
D) 2
-
A) 1
B) 4
C) 0
D) 2

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
16
Find the number of subsets of the set.
- is a day of the week
A) 128
B) 256
C) 124
D) 127
- is a day of the week
A) 128
B) 256
C) 124
D) 127

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
17
Find the number of subsets of the set.
- is an even number between 15 and 35
A) 1024
B) 32
C) 34
D) 5
- is an even number between 15 and 35
A) 1024
B) 32
C) 34
D) 5

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
18
Find the number of subsets of the set.
-
A) 508
B) 16
C) 1024
D) 512
-
A) 508
B) 16
C) 1024
D) 512

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
19
Find the complement of the set.
- is an integer strictly between 0 and 9 if is the set of all integers
A) is an integer
B) is an integer or
C) is an integer
D) is an integer or
- is an integer strictly between 0 and 9 if is the set of all integers
A) is an integer
B) is an integer or
C) is an integer
D) is an integer or

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
20
Find the complement of the set.
- is a whole number less than 6 if is the set of all whole numbers
A) is a whole number
B) is a whole number
C) is a whole number
D) is a whole number
- is a whole number less than 6 if is the set of all whole numbers
A) is a whole number
B) is a whole number
C) is a whole number
D) is a whole number

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
21
Decide whether the statement is true or false.
-
-

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
22
Decide whether the statement is true or false.
-
-

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
23
Decide whether the statement is true or false.
-
-

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
24
Decide whether the statement is true or false.
-
-

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
25
Decide whether the statement is true or false.
-
-

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
26
Decide whether the statement is true or false.
-
-

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
27
Decide whether the statement is true or false.
-
-

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
28
Decide whether the statement is true or false.
-
-

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
29
Decide whether the statement is true or false.
-
-

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
30
Let and . List the members of the indicated set, using set braces.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
31
Let and . List the members of the indicated set, using set braces.
-B'
A)
B)
C)
D)
-B'
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
32
Let and . List the members of the indicated set, using set braces.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
33
Let and . List the members of the indicated set, using set braces.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
34
Let and . List the members of the indicated set, using set braces.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
35
Let and . List the members of the indicated set, using set braces.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
36
Let and . List the members of the indicated set, using set braces.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
37
Let and . List the members of the indicated set, using set braces.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
38
Let and . List the members of the indicated set, using set braces.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
39
Let and . List the members of the indicated set, using set braces.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
40
Let be the smallest possible universal set that includes all of the crops listed; and let , and be the sets of five crops in Alabama, Arkansas, and Louisiana, respectively. Find the indicated set.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
41
Let be the smallest possible universal set that includes all of the crops listed; and let , and be the sets of five crops in Alabama, Arkansas, and Louisiana, respectively. Find the indicated set.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
42
Let be the smallest possible universal set that includes all of the crops listed; and let , and be the sets of five crops in Alabama, Arkansas, and Louisiana, respectively. Find the indicated set.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
43
Let be the smallest possible universal set that includes all of the crops listed; and let , and be the sets of five crops in Alabama, Arkansas, and Louisiana, respectively. Find the indicated set.
-L' A
A)
B)
C)
D)
-L' A
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
44
Let be the smallest possible universal set that includes all of the crops listed; and let , and be the sets of five crops in Alabama, Arkansas, and Louisiana, respectively. Find the indicated set.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
45
Let be the smallest possible universal set that includes all of the crops listed; and let , and be the sets of five crops in Alabama, Arkansas, and Louisiana, respectively. Find the indicated set.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
46
Let be the smallest possible universal set that includes all of the crops listed; and let , and be the sets of five crops in Alabama, Arkansas, and Louisiana, respectively. Find the indicated set.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
47
Let be the smallest possible universal set that includes all of the crops listed; and let , and be the sets of five crops in Alabama, Arkansas, and Louisiana, respectively. Find the indicated set.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
48
Let be the smallest possible universal set that includes all of the crops listed; and let , and be the sets of five crops in Alabama, Arkansas, and Louisiana, respectively. Find the indicated set.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
49
Let be the smallest possible universal set that includes all of the crops listed; and let , and be the sets of five crops in Alabama, Arkansas, and Louisiana, respectively. Find the indicated set.
-
A)
B)
C)
D)
-
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
50
Shade the Venn diagram to represent the set.
-
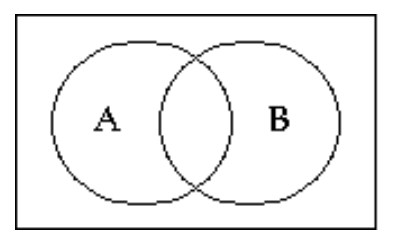
A)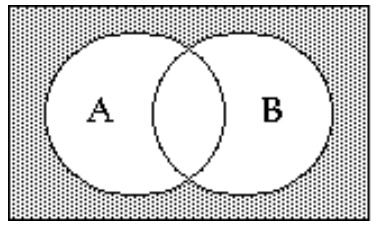
B)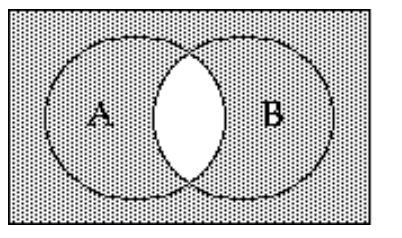
-

A)

B)


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
51
Shade the Venn diagram to represent the set.
-
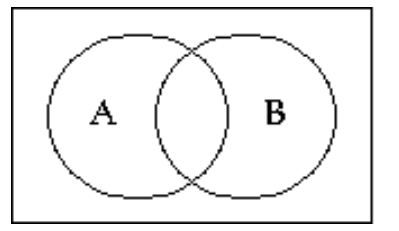
A)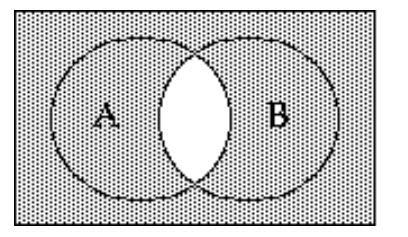
B)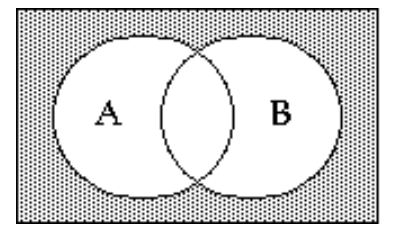
-

A)

B)


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
52
Shade the Venn diagram to represent the set.
-
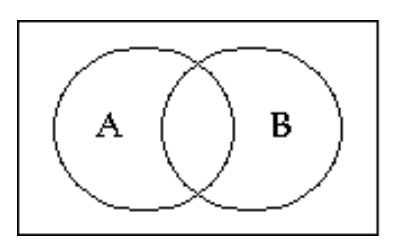
A)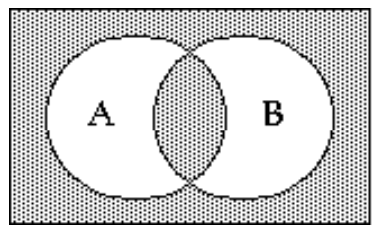
B)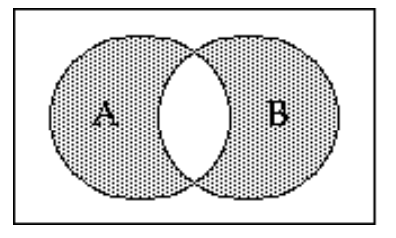
-

A)

B)


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
53
Shade the Venn diagram to represent the set.
-
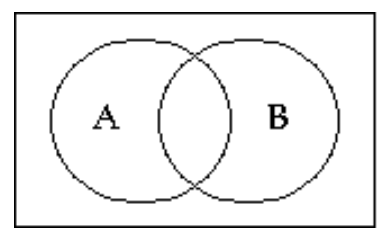
A)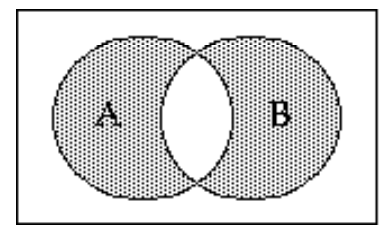
B)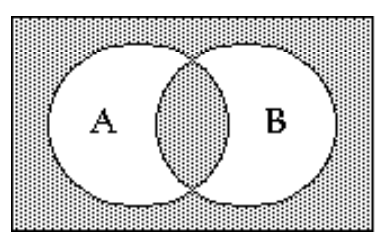
-

A)

B)


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
54
Shade the Venn diagram to represent the set.
-
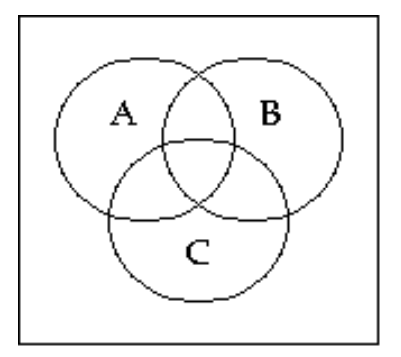
A)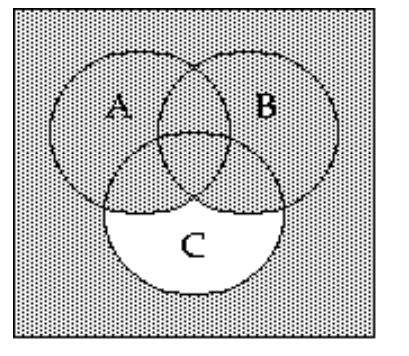
B)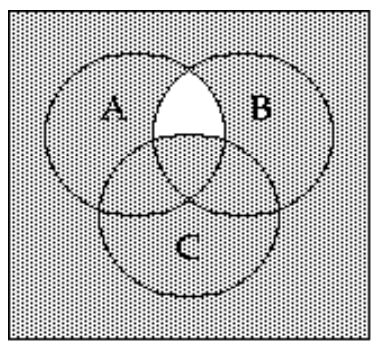
-

A)

B)


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
55
Shade the Venn diagram to represent the set.
-
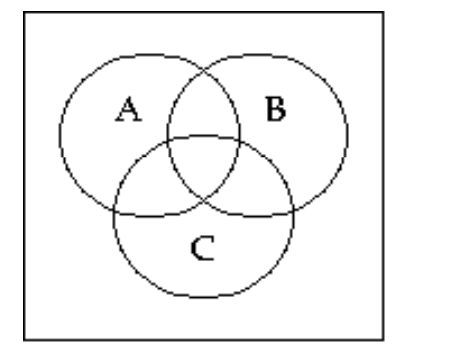
A)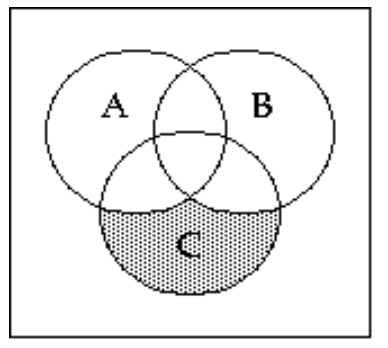
B)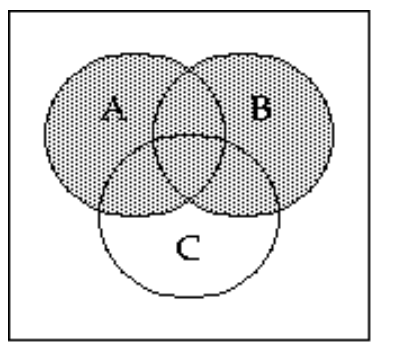
-

A)

B)


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
56
Shade the Venn diagram to represent the set.
-
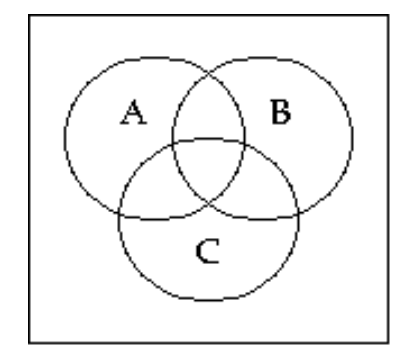
A)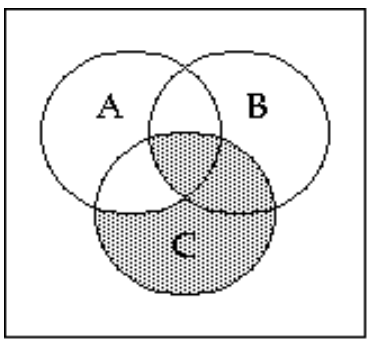
B)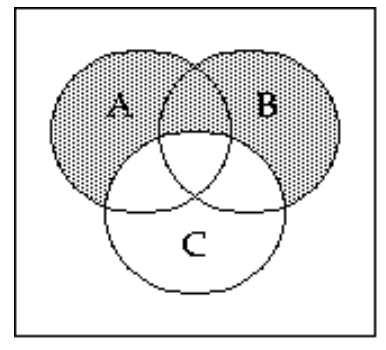
-

A)

B)


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
57
Shade the Venn diagram to represent the set.
-
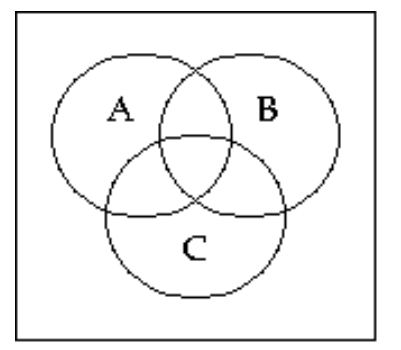
A)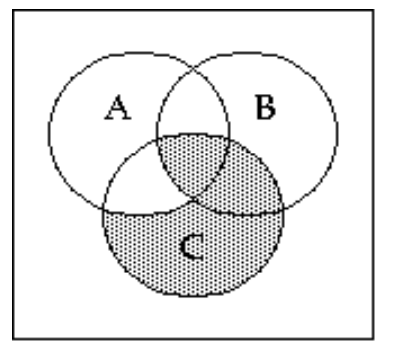
B)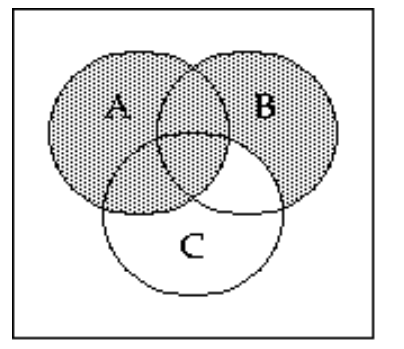
-

A)

B)


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
58
Shade the Venn diagram to represent the set.
-
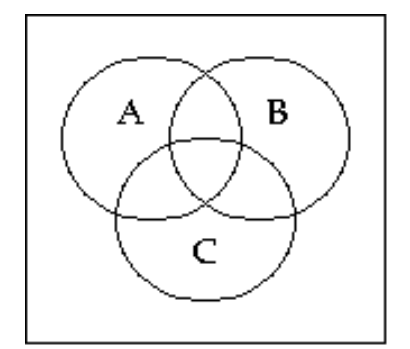
A)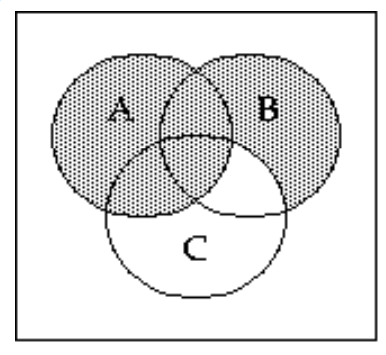
B)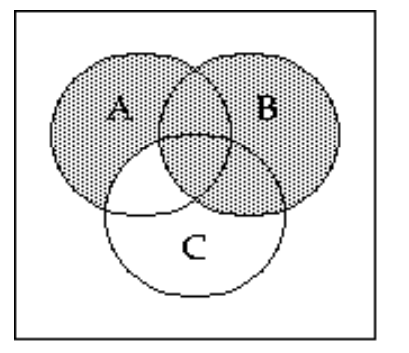
-

A)

B)


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
59
Shade the Venn diagram to represent the set.
-
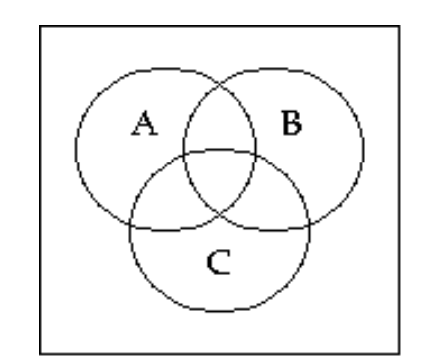
A)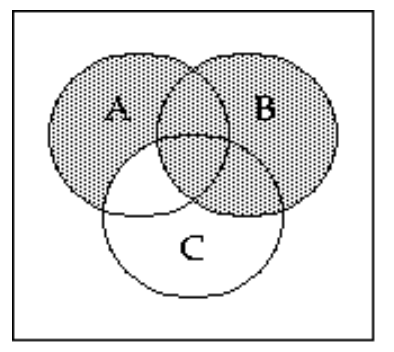
B)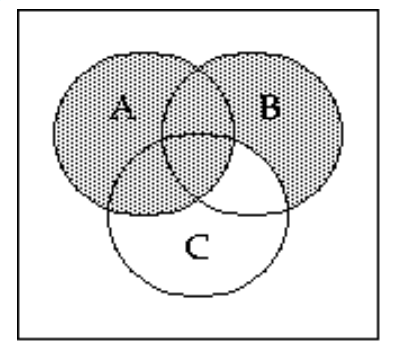
-

A)

B)


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
60
Use a Venn Diagram and the given information to determine the number of elements in the indicated set.
- , and . Find .
A) 43
B) 14
C) 46
D) 17
- , and . Find .
A) 43
B) 14
C) 46
D) 17

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
61
Use a Venn Diagram and the given information to determine the number of elements in the indicated set.
- , , and . Find .
A) 50
B) 46
C) 86
D) 30
- , , and . Find .
A) 50
B) 46
C) 86
D) 30

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
62
Use a Venn Diagram and the given information to determine the number of elements in the indicated set.
- , and . Find
A) 227
B) 398
C) 408
D) 312
- , and . Find
A) 227
B) 398
C) 408
D) 312

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
63
Use a Venn Diagram and the given information to determine the number of elements in the indicated set.
- , , and . Find
A) 20
B) 19
C) 17
D) 18
- , , and . Find
A) 20
B) 19
C) 17
D) 18

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
64
Use a Venn Diagram and the given information to determine the number of elements in the indicated set.
- , and . Find .
A) 35
B) 4
C) 38
D) 3
- , and . Find .
A) 35
B) 4
C) 38
D) 3

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
65
Use a Venn Diagram and the given information to determine the number of elements in the indicated set.
- , and . Find .
A) 5
B) 32
C) 4
D) 28
- , and . Find .
A) 5
B) 32
C) 4
D) 28

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
66
Use a Venn Diagram and the given information to determine the number of elements in the indicated set.
- , and . Find .
A) 3
B) 4
C) 12
D) 15
- , and . Find .
A) 3
B) 4
C) 12
D) 15

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
67
Use a Venn diagram to decide if the statement is true or false.
-
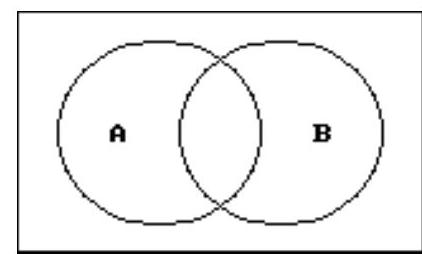
-


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
68
Use a Venn diagram to decide if the statement is true or false.
-
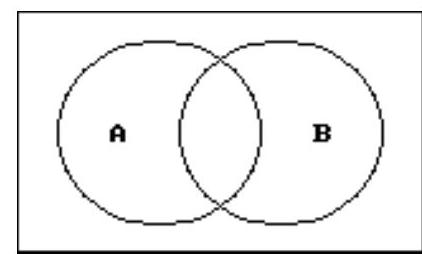
-


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
69
Use a Venn diagram to decide if the statement is true or false.
-
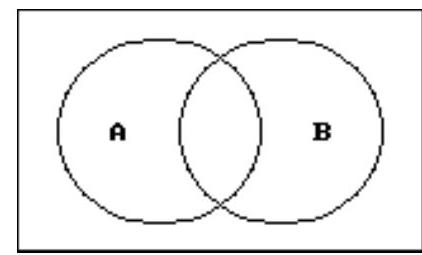
-


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
70
Use a Venn diagram to decide if the statement is true or false.
-
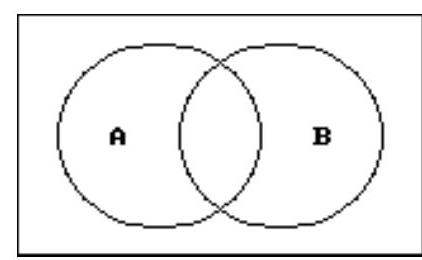
-


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
71
Use a Venn diagram to decide if the statement is true or false.
-
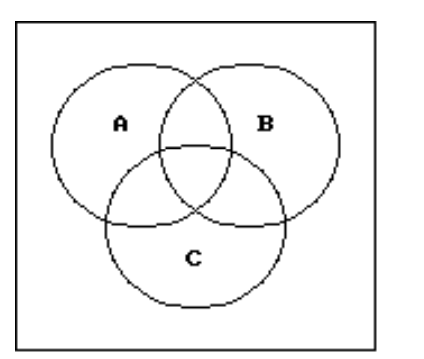
-


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
72
Use a Venn diagram to decide if the statement is true or false.
-
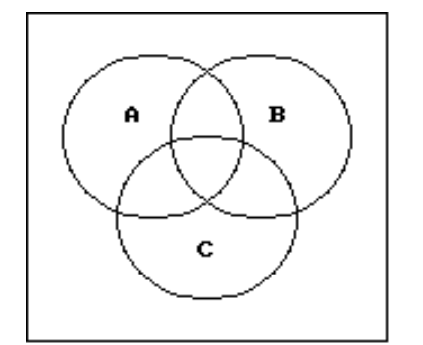
-


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
73
Use a Venn diagram to decide if the statement is true or false.
-
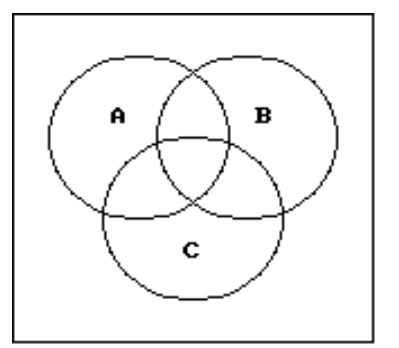
-


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
74
Use a Venn diagram to decide if the statement is true or false.
-
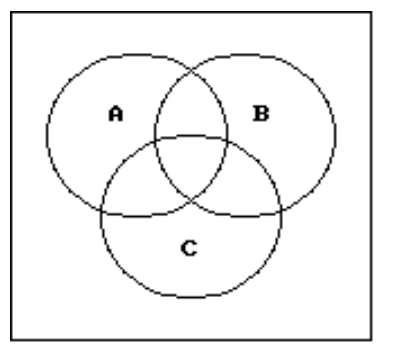
-


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
75
Use a Venn diagram to decide if the statement is true or false.
-
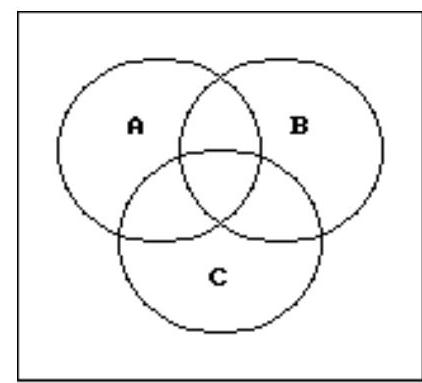
-


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
76
Use a Venn diagram to decide if the statement is true or false.
-(A ? B) ? (A ? C) = A ? (B ? C)
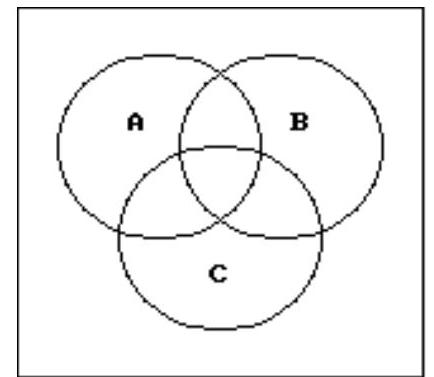
-(A ? B) ? (A ? C) = A ? (B ? C)


Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
77
Use a Venn diagram to answer the question.
-At East Zone University (EZU) there are 683 students taking College Algebra or Calculus. 281 are taking College Algebra, 456 are taking Calculus, and 54 are taking both College Algebra and Calculus. How many are taking Algebra but not Calculus?
A)6 29
B) 227
C) 173
D) 402
-At East Zone University (EZU) there are 683 students taking College Algebra or Calculus. 281 are taking College Algebra, 456 are taking Calculus, and 54 are taking both College Algebra and Calculus. How many are taking Algebra but not Calculus?
A)6 29
B) 227
C) 173
D) 402

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
78
Use a Venn diagram to answer the question.
-At East Zone University (EZU) there are 688 students taking College Algebra or Calculus. 495 are taking College Algebra, 210 are taking Calculus, and 17 are taking both College Algebra and Calculus. How many are taking Calculus but not Algebra?
A) 671
B) 461
C) 478
D) 193
-At East Zone University (EZU) there are 688 students taking College Algebra or Calculus. 495 are taking College Algebra, 210 are taking Calculus, and 17 are taking both College Algebra and Calculus. How many are taking Calculus but not Algebra?
A) 671
B) 461
C) 478
D) 193

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
79
Use a Venn diagram to answer the question.
-A local television station sends out questionnaires to determine if viewers would rather see a documentary, an interview show, or reruns of a game show. There were 900 responses with the following results:
270 were interested in an interview show and a documentary, but not reruns;
36 were interested in an interview show and reruns, but not a documentary;
126 were interested in reruns but not an interview show;
216 were interested in an interview show but not a documentary;
90 were interested in a documentary and reruns;
54 were interested in an interview show and reruns;
72 were interested in none of the three.
How many are interested in exactly one kind of show?
A) 422
B) 432
C) 412
D) 442
-A local television station sends out questionnaires to determine if viewers would rather see a documentary, an interview show, or reruns of a game show. There were 900 responses with the following results:
270 were interested in an interview show and a documentary, but not reruns;
36 were interested in an interview show and reruns, but not a documentary;
126 were interested in reruns but not an interview show;
216 were interested in an interview show but not a documentary;
90 were interested in a documentary and reruns;
54 were interested in an interview show and reruns;
72 were interested in none of the three.
How many are interested in exactly one kind of show?
A) 422
B) 432
C) 412
D) 442

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck
80
Use a Venn diagram to answer the question.
-A survey of 180 families showed that
67 had a dog;
52 had a cat;
22 had a dog and a cat;
70 had neither a cat nor a dog, and in addition did not have a parakeet;
4 had a cat, a dog, and a parakeet.
How many had a parakeet only?
A) 28
B) 18
C) 23
D) 13
-A survey of 180 families showed that
67 had a dog;
52 had a cat;
22 had a dog and a cat;
70 had neither a cat nor a dog, and in addition did not have a parakeet;
4 had a cat, a dog, and a parakeet.
How many had a parakeet only?
A) 28
B) 18
C) 23
D) 13

Unlock Deck
Unlock for access to all 240 flashcards in this deck.
Unlock Deck
k this deck


