Deck 5: Probability Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/49
Play
Full screen (f)
Deck 5: Probability Distributions
1
Identify each of the following as a discrete or continuous random variable.
Distance traveled for a migrating bird.
Distance traveled for a migrating bird.
Continuous
2
Each of the judges in a popular dancing contest assign point from 3 through 5 to each participating couple. Let X be the sum of the two scores assigned to a particular couple. List the possible values for the sum of the two scores and also the pairs of scores that result in that sum.
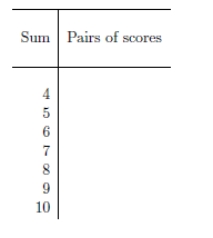


3
A rent a car company has two types of vehicles: compact (C) and full size (F). For two consecutive months, the manager recorded the type with the highest customer acceptance. List the possible outcomes, in alphabetical order; each outcome must be followed by the number of months that a full size car has the highest acceptance. That is: Letter-Letter Number
C-C 0, C-F 1, C-S 0, F-C 1, F-F 2, F-S 1, S-C 0, S-F 1, S-S 0
4
A junior college student is planning her spring semester; there are six courses available and she must choose four. The courses are:
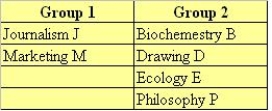
A) Make a list, in alphabetical order, of the outcomes. (Use B, D, E, J, M, and P to denote the five courses).
B) Let Y be the number of courses in Group 2 included.
C) Use the information obtained in (A) and (B) to complete the following table.

A) Make a list, in alphabetical order, of the outcomes. (Use B, D, E, J, M, and P to denote the five courses).
B) Let Y be the number of courses in Group 2 included.
C) Use the information obtained in (A) and (B) to complete the following table.


Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
5
The events corresponding to the distinct values of a random variable X are incompatible.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
6
A random variable can be ______ or continuous.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
7
If X represents the number of times that a head is followed by a tail obtained in four tosses of a fair coin, find the probability distribution of X. Write the probabilities using decimal numbers.


Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
8
Let X be the number of vowels in 50 words taken at random from a dictionary. If f(2) = .12 , f(3) = .2, f(4) = .15, and f(5) = .17, find f(6).
A) .53
B) .48
C) .36
D) .56
A) .53
B) .48
C) .36
D) .56

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
9
Probability distributions are sample based and then susceptible to variation on different occasions of sampling.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
10
Let the random variable X represent the sum of points in a tile taken from the dominoes set shown below.
 What is the probability of 9? Write your answer as a fraction reduced to lowest terms.
What is the probability of 9? Write your answer as a fraction reduced to lowest terms.
 What is the probability of 9? Write your answer as a fraction reduced to lowest terms.
What is the probability of 9? Write your answer as a fraction reduced to lowest terms.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
11
Determine how many of the following are a legitimate probability distribution. 
A) 0
B) 3
C) 1
D) 2

A) 0
B) 3
C) 1
D) 2

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
12
Consider the probability distribution given by the function
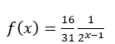 for
for 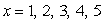 Find f(5). Round your answer to three decimal places.
Find f(5). Round your answer to three decimal places.
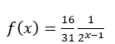 for
for 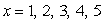 Find f(5). Round your answer to three decimal places.
Find f(5). Round your answer to three decimal places.
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
13
The probability distribution of X is given by the function
![The probability distribution of X is given by the function for x = 2, 3, 4, 5. Find P[X = 4 ]. Round your answer to two decimal places.](https://storage.examlex.com/TB10841/11ef019b_aac2_3efd_a255_93081efe3b69_TB10841_00.jpg) for x = 2, 3, 4, 5.
for x = 2, 3, 4, 5.
Find P[X = 4 ]. Round your answer to two decimal places.
![The probability distribution of X is given by the function for x = 2, 3, 4, 5. Find P[X = 4 ]. Round your answer to two decimal places.](https://storage.examlex.com/TB10841/11ef019b_aac2_3efd_a255_93081efe3b69_TB10841_00.jpg) for x = 2, 3, 4, 5.
for x = 2, 3, 4, 5.Find P[X = 4 ]. Round your answer to two decimal places.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
14
Your scores (0-50) in the six homework assignments for a course are: 46 46 46 50 50 50. The instructor will add the scores of two randomly selected assignment, this number will be your homework grade. Let X denote the sum of the scores of the two selected assignment. Complete the following table of probability distribution of X. Round the probabilities to two decimal places when necessary.
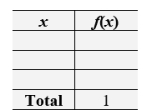


Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
15
A probability distribution is partially given in the following table with the additional information that the even values of X are equally likely. Determine the missing entries in the table.



Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
16
Let X be the number of vowels used in the name of each U.S. state. Use the following table to calculate:
A)
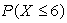
B)
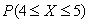

A)
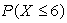
B)
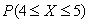


Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
17
With X denoting the number of 1's or 2's in two rolls of a fair die, calculate the mean of X. Round your answer to two decimal places.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
18
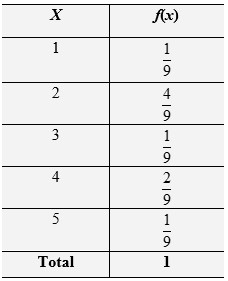
Use the information in the table below to calculate the expected value of x. Round your answer to three decimal places.


Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
19
Calculate the variance of the distribution of X 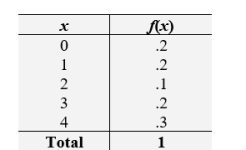
A) 2.08
B) 2.16
C) 2.3
D) 2.36

A) 2.08
B) 2.16
C) 2.3
D) 2.36

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
20
Calculate the standard deviation of the distribution of X. 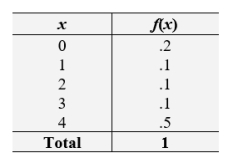
A) 1.84
B) 1.62
C) 1.52
D) 1.48

A) 1.84
B) 1.62
C) 1.52
D) 1.48

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
21
The variance rather than the standard deviation, is the appropriate measure of spread.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
22
Given the following probability distribution, find:

A) E(X)
B) 2
C)

A) E(X)
B) 2
C)

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
23
Is the model of Bernoulli trials plausible in the following situation?
Students in a literature course must read a book, the time spent reading the book is recorded.
Students in a literature course must read a book, the time spent reading the book is recorded.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
24
In Bernoulli Trials, if P(S) = p, then P(F) = 1 - p.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
25
If elements are sampled from a small dichotomous population at random and ______ replacement, the conditions for Bernoulli trials are satisfied.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
26
A cookie jar contains 42 cookies of which 10 are oatmeal, 18 are sugar, and 14 are macaroon. Consider 5 successive draws of one cookie from the jar and suppose the selected cookie is returned to the jar. If the appearance of an oatmeal cookie is the event of interest, determine the numerical value of p. Round your answer to two decimal places

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
27
Consider Bernoulli trials with success probability p = 0.7.
A) Find the probability that three trials result in all failures.
B) Find the probability that the first failure occurs in the third trial.
Round your answer to three decimal places.
A) Find the probability that three trials result in all failures.
B) Find the probability that the first failure occurs in the third trial.
Round your answer to three decimal places.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
28
The accompanying table shows the percentages of students in the state university system when classified according to gender and status as residents of that state.
 Suppose that a selection of a person is considered a trial and it is a success when the person selected is a resident of that state.
Suppose that a selection of a person is considered a trial and it is a success when the person selected is a resident of that state.
Three persons are selected at random. What is the probability that none is a state resident? Round your answer to three decimal places.
 Suppose that a selection of a person is considered a trial and it is a success when the person selected is a resident of that state.
Suppose that a selection of a person is considered a trial and it is a success when the person selected is a resident of that state.Three persons are selected at random. What is the probability that none is a state resident? Round your answer to three decimal places.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
29
The accompanying table shows the percentages of students in the state university system when classified according to gender and status as residents of that state.
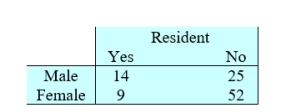 Suppose that a selection of a person is considered a trial and it is a success when the person selected is a resident of that state.
Suppose that a selection of a person is considered a trial and it is a success when the person selected is a resident of that state.
Five females are selected at random. What is the probability that none is a state resident? Round your answer to three decimal places.
 Suppose that a selection of a person is considered a trial and it is a success when the person selected is a resident of that state.
Suppose that a selection of a person is considered a trial and it is a success when the person selected is a resident of that state.Five females are selected at random. What is the probability that none is a state resident? Round your answer to three decimal places.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
30
The accompanying table shows the percentages of students in the state university system when classified according to gender and status as residents of that state.
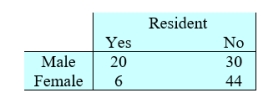 Suppose that a selection of a person is considered a trial and it is a success when the person selected is a resident of that state.
Suppose that a selection of a person is considered a trial and it is a success when the person selected is a resident of that state.
Two males and two females are selected at random. What is the probability that none is a state resident? Round your answer to three decimal places.
 Suppose that a selection of a person is considered a trial and it is a success when the person selected is a resident of that state.
Suppose that a selection of a person is considered a trial and it is a success when the person selected is a resident of that state.Two males and two females are selected at random. What is the probability that none is a state resident? Round your answer to three decimal places.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
31
Find the probability of 5 successes in 7 Bernoulli trials with success probability 0.7 for each trial. Round your answer to three decimal places.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
32
If p is the probability of success and q = 1 - p, then the probability distribution of X for four Bernoulli trials is:
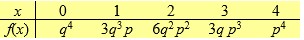
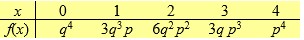

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
33
If p is the probability of success and q is the probability of failure, then the probability of X = 5 for 8 Bernoulli trials is:
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
34
Use the Bernoulli Table (Appendix B, Table 2) to find P[X 6] for n = 8 and p = 0.7.
A) .255
B) .745
C) .265
D) .735
A) .255
B) .745
C) .265
D) .735

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
35
Consider the binomial distribution with 17 trials and success probability 0.68. Find its:
A) Mean
B) Variance
C) Standard Deviation
A) Mean
B) Variance
C) Standard Deviation

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
36
A shooting athlete using a shotgun has an 81% chance of success (shot on target). Let X denote the number of successes in the next six rounds. Assuming the results for different rounds are independent, calculate P[X = 3 or 5]. Round your answer to two decimal places.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
37
About 78% of children in a neighborhood have a bicycle. Suppose n = 4 children are randomly selected. Find the probability that at most two have a bicycle. Round your answer to two decimal places.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
38
Suppose 30% of the urban population is 18 years old or younger. Five residents of that city are selected at random; find the probability that two of the selected five persons are 18 years old or younger.
A) .13
B) .18
C) .26
D) .31
A) .13
B) .18
C) .26
D) .31

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
39
Given that n = 25 and p0 = .35, find:
A) The lower control limit.
B) The upper control limit.
A) The lower control limit.
B) The upper control limit.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
40
Given that the lower control limit is 0.12 and p0 = .5, find the value of n.
A) 5
B) 11
C) 16
D) Cannot be determined
A) 5
B) 11
C) 16
D) Cannot be determined

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
41
Use the Poisson Table (Appendix A, Table 3) to find P [ X 4] for rate parameter m = 2.4
A) .779
B) 0.430
C) .221
D) .096
A) .779
B) 0.430
C) .221
D) .096

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
42
Consider a Poisson random variable with rate parameter m = 4. Find its:
(a) Mean
(b) Variance
(c) Standard Deviation
(a) Mean
(b) Variance
(c) Standard Deviation

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
43
Is the Poisson distribution a suitable approximation for to the binomial distribution with n = 55 and p = .03

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
44
The probability of red coming up on a roulette wheel that has 18 red, 18 black, and 2 green slots is 18/38 or about .474. If you bet on red a large number of times, what proportion of times will you win. Explain your reasoning.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
45
John and two of his friends have one-on-one basketball tournaments almost every week. Each person plays each other person once. Let X be the number of games that John wins next week X. Based on the results of the games over the past year, John constructs the following probability distribution for X.
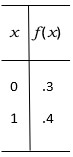
Find
(a) The expected number of wins.
(b) The standard deviation of the number of wins.
(c) Explain how John should use the results of previous games to construct the tabled probability distribution.

Find
(a) The expected number of wins.
(b) The standard deviation of the number of wins.
(c) Explain how John should use the results of previous games to construct the tabled probability distribution.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
46
Given the following probability distribution for a random variable X,
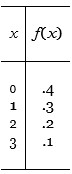
Find
(a) E ( X )
(b) 2 = Var ( X )
(c) standard deviation of X.

Find
(a) E ( X )
(b) 2 = Var ( X )
(c) standard deviation of X.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
47
You are traveling to Stockholm, Sweden next month when the average temperature is -1.5 degrees Celsius. Treating this as the expected value of a random variable X, use the properties of expectation to determine the expected value of this temperature, Y , in degrees Fahrenheit. Recall that
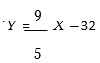
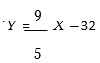

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
48
About 75% of dog owners buy holiday presents for their dogs. Sup- pose n = 3 dog owners are randomly selected. Use the formula for the binomial distribution to find the probability of:
(a) Two or more buy their dog holiday presents.
(b) At most two buy their dog holiday presents.
(c) Find the expected number of persons, in the sample, who buy their dog holiday presents.
(a) Two or more buy their dog holiday presents.
(b) At most two buy their dog holiday presents.
(c) Find the expected number of persons, in the sample, who buy their dog holiday presents.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
49
The manager of a satellite TV service states that the rate of
interruption of services is .4 per month. Use the Poisson distribution in Table 3 of Appendix A to find
(a) Zero interruptions in one month.
(b) One or more interruptions in one month.
(c) Exact two interruptions in 3 consecutive months.
interruption of services is .4 per month. Use the Poisson distribution in Table 3 of Appendix A to find
(a) Zero interruptions in one month.
(b) One or more interruptions in one month.
(c) Exact two interruptions in 3 consecutive months.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck


