Deck 6: Uncertainty and the Emergence of Insurance
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/40
Play
Full screen (f)
Deck 6: Uncertainty and the Emergence of Insurance
1
A probability distribution with a finite number of events is called a discrete probability distribution.
True
2
The expected monetary return of a lottery, gamble, or investment, determined by taking a weighted average of the monetary prizes offered using the associated probabilities as weights is called
A) expected rate of return
B) expected utility
C) expected monetary value
A) expected rate of return
B) expected utility
C) expected monetary value
expected monetary value
3
Agents _________ simply choose the option that maximizes their expected monetary payoff; they also evaluate the __________ of each payoff.
A) do not, unselfishness
B) do not, utility
C) do, utility
A) do not, unselfishness
B) do not, utility
C) do, utility
do not, utility
4
Risk pooling relies upon
A) the average annual amount of rainfall
B) a property of random variables
C) diving headfirst into the shallow end
A) the average annual amount of rainfall
B) a property of random variables
C) diving headfirst into the shallow end

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
5
The sum of the various values that a random variable can take on multiplied by the associated probability is known as
A) expected value
B) mean
C) weighted average
D) All of the answers are correct
A) expected value
B) mean
C) weighted average
D) All of the answers are correct

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
6
Xavier, Yolanda, and Zachary are considering whether to pool their funds to buy into a lottery. There is a 20% chance that they will win big and make $8 million dollars, a 40% chance that they will win second prize and make $2 million, and a 40% chance that they will lose and win nothing. The entrance fee to participate in this lottery is $3 million. The partners decide whether or not to play by majority vote. Assume that Xavier has utility function u(x) = x². The other two partners have utility function u(x) = x, where x is the total amount of money won in the lottery. Will the partners buy in?
A) All three will vote to buy in, so the partnership as a whole will buy in
B) Only Xavier will vote to buy in, so the partnership as a whole will not buy in
C) Yolanda and Zachary will vote to buy in, so the partnership as a whole will buy in
A) All three will vote to buy in, so the partnership as a whole will buy in
B) Only Xavier will vote to buy in, so the partnership as a whole will not buy in
C) Yolanda and Zachary will vote to buy in, so the partnership as a whole will buy in

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
7
The introduction of insurance makes sense only in a society where something is
A) expensive
B) uncertain or unknown
C) heavily advertised
A) expensive
B) uncertain or unknown
C) heavily advertised

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
8

Refer to Exhibit 6-1 for the probability distribution for four different ages that are spread equally throughout a hypothetical population. What is the expected age of the next person to walk into the classroom?
A) 45 years
B) 35 years
C) 55 years

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
9
Risk neutral is a characteristic of an agent who has a convex utility function (increasing marginal utility).

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
10
A probability distribution with a finite number of events is called a continuous probability distribution.

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
11
The distribution that tells us the likelihood that a given random variable will take on any given value is called a(n)
A) probability distribution
B) income distribution
C) variable distribution
A) probability distribution
B) income distribution
C) variable distribution

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
12
A continuous probability distribution is a probability distribution with a(n)
A) infinite number of events
B) finite number of events
C) constant number of events
A) infinite number of events
B) finite number of events
C) constant number of events

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
13
Expected utility is the expected utility of a lottery, gamble, or investment, determined by taking a weighted average of the utility of the monetary prizes offered using the associated probabilities as weights.

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
14
Risk averse is a characteristic of an agent who has a concave utility function (diminishing marginal utility).

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
15
Variance is a measure that tries to capture the variability of a random variable by looking at the expected squared deviation of the random variable from its mean.

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
16
The hypothesis that states that, when people are faced with risk, they assess the possible payoffs in terms of utility and then choose the gamble that yields the payoff with the highest expected utility is known as the expected utility hypothesis.

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
17
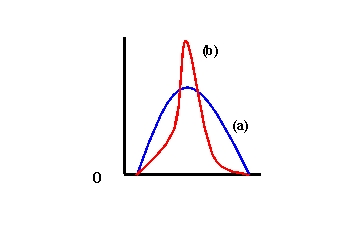
Refer to Exhibit 6-2. Which curve has the greater variance?
A) (a)
B) (b)
C) It is necessary to calculate the variances in order to answer

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
18
Expected monetary value is the expected utility of a lottery, gamble, or investment, determined by taking a weighted average of the utility of the monetary prizes offered using the associated probabilities as weights.

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
19
Risk preference is a characteristic of an agent who has a convex utility function (increasing marginal utility).

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
20
A probability distribution is a measure that tries to capture the variability of a random variable by looking at the expected squared deviation of the random variable from its mean.

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
21
Describe the difference between a discrete and a continuous probability distribution.

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
22
For Kay Afar, one way of assigning utility to an apple gives a number of 12. Another way gives a number of 30. The first way of assigning utility gives a number of 36 for a banana; the other way gives a number of 217. Either way, Kay chooses the banana. What kind of utility is illustrated by this example?
A) ordinal
B) cardinal
C) agricultural
A) ordinal
B) cardinal
C) agricultural

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
23
The main behavioral assumption that economists use in analyzing the choices that people make under conditions of uncertainty is the
A) expected monetary value hypothesis
B) expected consumption of utility hypothesis
C) expected utility hypothesis
A) expected monetary value hypothesis
B) expected consumption of utility hypothesis
C) expected utility hypothesis

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
24
A risk-averse agent will
A) reject a "fair gamble"
B) be indifferent to a "fair gamble"
C) accept a "fair gamble"
A) reject a "fair gamble"
B) be indifferent to a "fair gamble"
C) accept a "fair gamble"

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
25
If utility is measured in a way that not only the utility numbers assigned to bundles are meaningful, but also their differences, then we say that we are using
A) cardinal utility
B) ordinal utility
C) expected utility
A) cardinal utility
B) ordinal utility
C) expected utility

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
26
An agent who has a linear utility function, which implies that the agent will choose between gambles strictly on the basis of their expected monetary value, is risk
A) averse
B) neutral
C) preferring
A) averse
B) neutral
C) preferring

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
27
Xavier, Yolanda, and Zachary are considering whether to pool their funds to buy into a lottery. There is a 20% chance that they will win big and make $8 million dollars, a 40% chance that they will win second prize and make $2 million, and a 40% chance that they will lose and win nothing. The entrance fee to participate in this lottery is $2 million. The partners decide whether or not to play by majority vote. Assume that Xavier has utility function u(x) = x². The other two partners have utility function u(x) = x, where x is the total amount of money won in the lottery. Will the partners buy in?
A) All three will vote to buy in, so the partnership as a whole will buy in
B) Only Xavier will vote to buy in, so the partnership as a whole will not buy in
C) Yolanda and Zachary will vote to buy in, so the partnership as a whole will buy in
A) All three will vote to buy in, so the partnership as a whole will buy in
B) Only Xavier will vote to buy in, so the partnership as a whole will not buy in
C) Yolanda and Zachary will vote to buy in, so the partnership as a whole will buy in

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
28
(a)
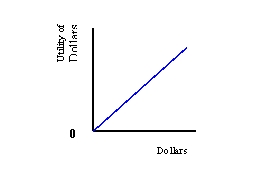
(b)
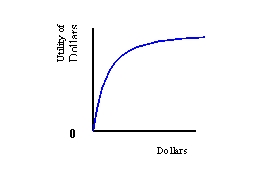
(c)
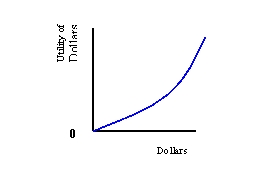
Refer to Exhibit 6-3. Which utility function is risk averse?
A) (a)
B) (b)
C) (c)

(b)

(c)

Refer to Exhibit 6-3. Which utility function is risk averse?
A) (a)
B) (b)
C) (c)

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
29
The analogy of Fahrenheit and Celsius temperature scales best fits
A) additive utility
B) ordinal utility
C) cardinal utility
A) additive utility
B) ordinal utility
C) cardinal utility

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
30
A risk-preferring agent will
A) reject a "fair gamble"
B) be indifferent to a "fair gamble"
C) accept a "fair gamble"
A) reject a "fair gamble"
B) be indifferent to a "fair gamble"
C) accept a "fair gamble"

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
31
What are the characteristics of a risk averse agent?

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
32
An agent who buys high-priced insurance is most likely
A) risk neutral
B) risk averse
C) risk preferring
A) risk neutral
B) risk averse
C) risk preferring

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
33
The theory of expected utility is
A) accepted by all economists
B) not without its detractors
C) able to explain all consumer choices
A) accepted by all economists
B) not without its detractors
C) able to explain all consumer choices

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
34
(a)

(b)

(c)

Refer to Exhibit 6-3. Which utility function is risk neutral?
A) (a)
B) (b)
C) (c)

(b)

(c)

Refer to Exhibit 6-3. Which utility function is risk neutral?
A) (a)
B) (b)
C) (c)

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
35
Explain why economists generally assume that agents have cardinal utility functions.

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
36
A risk-neutral agent will
A) reject a "fair gamble"
B) be indifferent to a "fair gamble"
C) accept a "fair gamble"
A) reject a "fair gamble"
B) be indifferent to a "fair gamble"
C) accept a "fair gamble"

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
37
A risk-preferring agent will most likely not buy insurance unless it has a
A) low price
B) neutral price
C) high price
A) low price
B) neutral price
C) high price

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
38
Why not maximize expected monetary returns?

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
39
Consider the test in Experimental Teaser 7 at the beginning of the chapter. How would you predict a risk preferring agent to behave in this experiment?

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck
40
(a)

(b)

(c)

Refer to Exhibit 6-3. Which utility function is risk preferring?
A) (a)
B) (b)
C) (c)

(b)

(c)

Refer to Exhibit 6-3. Which utility function is risk preferring?
A) (a)
B) (b)
C) (c)

Unlock Deck
Unlock for access to all 40 flashcards in this deck.
Unlock Deck
k this deck


