Deck 6: Sampling and Sampling Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/147
Play
Full screen (f)
Deck 6: Sampling and Sampling Distributions
1
A sample of size 25 is selected at random from a finite population.If the finite population correction factor is 0.80,then the population size is:
A)121
B)96
C)75
D)100
A)121
B)96
C)75
D)100
121
2
Random samples of size 36 are taken from an infinite population whose mean is 80 and standard deviation is 18.The standard error of the sample mean is:
A)18
B)15
C)3
D)2
A)18
B)15
C)3
D)2
3
3
Why is the central limit theorem important in statistics?
A)Because for a large sample size n,it says the population is approximately normal.
B)Because for any population,it says the sampling distribution of the sample mean is approximately normal,regardless of the shape of the population.
C)Because for a large sample size n,it says the sampling distribution of the sample mean is approximately normal,regardless of the shape of the population.
D)Because for any sample size n,it says the sampling distribution of the sample mean is approximately normal.
A)Because for a large sample size n,it says the population is approximately normal.
B)Because for any population,it says the sampling distribution of the sample mean is approximately normal,regardless of the shape of the population.
C)Because for a large sample size n,it says the sampling distribution of the sample mean is approximately normal,regardless of the shape of the population.
D)Because for any sample size n,it says the sampling distribution of the sample mean is approximately normal.
Because for a large sample size n,it says the sampling distribution of the sample mean is approximately normal,regardless of the shape of the population.
4
The standard deviation of the sampling distribution of the sample mean is also called the:
A)minimum sample factor.
B)standard error of the mean.
C)finite population correction factor.
D)population standard deviation.
A)minimum sample factor.
B)standard error of the mean.
C)finite population correction factor.
D)population standard deviation.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
5
What is the name of the parameter that determines the shape of the chi-square distribution?
A)mean
B)variance
C)proportion
D)degrees of freedom
A)mean
B)variance
C)proportion
D)degrees of freedom

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
6
The sampling distribution of the mean is a distribution of:
A)individual population values.
B)individual sample values.
C)sample statistics.
D)population parameters.
A)individual population values.
B)individual sample values.
C)sample statistics.
D)population parameters.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
7
A sample of size n is selected at random from an infinite population.As n increases,which of the following statements is true?
A)The population standard deviation decreases.
B)The standard error of the sample mean decreases.
C)The population standard deviation increases.
D)The standard error of the sample mean increases.
A)The population standard deviation decreases.
B)The standard error of the sample mean decreases.
C)The population standard deviation increases.
D)The standard error of the sample mean increases.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
8
In examining the invoices issued by a company,an auditor finds that the dollar amounts of invoices have a mean of $1,732 and a standard deviation of $298.What is the probability that for a sample of 45 invoices,the average invoice is greater than $1,800?
A)0.563
B)0.063
C)0.437
D)0.937
A)0.563
B)0.063
C)0.437
D)0.937

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
9
Which of the following statements is true regarding the standard error of the mean?
A)It is equal to the population variance divided by the square root of n.
B)It is equal to the population standard deviation divided by the sample size n.
C)It is equal to the population variance divided by (n -1).
D)It is equal to the population standard deviation divided by the square root of n.
A)It is equal to the population variance divided by the square root of n.
B)It is equal to the population standard deviation divided by the sample size n.
C)It is equal to the population variance divided by (n -1).
D)It is equal to the population standard deviation divided by the square root of n.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
10
If all possible samples of size n are drawn from an infinite population with a mean of 20 and a standard deviation of 5,then the standard error of the sampling distribution of sample means is equal to 1.0 only for samples of size:
A)5
B)15
C)20
D)25
A)5
B)15
C)20
D)25

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
11
If the standard error of the sampling distribution of the sample proportion is 0.0229 for samples of size 400,then the population proportion must be either:
A)0.4 or 0.6
B)0.5 or 0.5
C)0.2 or 0.8
D)0.3 or 0.7
A)0.4 or 0.6
B)0.5 or 0.5
C)0.2 or 0.8
D)0.3 or 0.7

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
12
In a recent survey of high school students,it was found that the average amount of money spent on entertainment each week was normally distributed with a mean of $52.30 and a standard deviation of $18.23.Assuming these values are representative of all high school students,what is the probability that for a sample of 25,the average amount spent by each student exceeds $60?
A)0.3372
B)0.0174
C)0.1628
D)0.4826
A)0.3372
B)0.0174
C)0.1628
D)0.4826

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
13
If a sample of size 100 is taken from a population whose standard deviation is equal to 100,then the standard error of the mean is equal to:
A)10
B)100
C)1,000
D)10,000
A)10
B)100
C)1,000
D)10,000

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
14
Which of the following distributions is used to determine the sampling distribution of the sample variance?
A)normal distribution
B)binomial distribution
C)chi-square distribution
D)Poisson distribution
A)normal distribution
B)binomial distribution
C)chi-square distribution
D)Poisson distribution

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
15
As a general rule,the normal distribution is used to approximate the sampling distribution of the sample proportion only if:
A)the sample size n is greater than 30.
B)the population proportion P is close to 0.50.
C)the underlying population is normal.
D)nP(1 - P)> 5.
A)the sample size n is greater than 30.
B)the population proportion P is close to 0.50.
C)the underlying population is normal.
D)nP(1 - P)> 5.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
16
If all possible samples of size n are drawn from an infinite population with a mean μ and a standard deviation σ,then the standard error of the sampling distribution of sample mean is inversely proportional to:
A)μ
B)σ
C)n
D)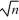
A)μ
B)σ
C)n
D)
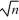

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
17
The interval within which a sample mean has a high probability of occurring,given that the population mean and variance is known,is called a(n):
A)confidence interval.
B)rejection interval.
C)acceptance interval.
D)decision interval.
A)confidence interval.
B)rejection interval.
C)acceptance interval.
D)decision interval.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
18
In a recent survey of college professors,it was found that the average amount of money spent on entertainment each week was normally distributed with a mean of $95.25 and a standard deviation of $27.32.What is the probability that the average spending of a sample of 25 randomly-selected professors will exceed $102.50?
A)0.0918
B)0.1064
C)0.3936
D)0.4082
A)0.0918
B)0.1064
C)0.3936
D)0.4082

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
19
The number of students using the ATM on campus daily is normally distributed with a mean of 237.6 and a standard deviation of 26.3.For a random sample of 55 days,what is the probability that the ATM usage averaged more than 230 students per day?
A)0.9756
B)0.9483
C)0.9838
D)0.9524
A)0.9756
B)0.9483
C)0.9838
D)0.9524

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
20
The amount of time that you have to wait before seeing the doctor in the doctor's office is normally distributed with a mean of 15.2 minutes and a standard deviation of 15.2 minutes.If you take a random sample of 35 patients,what is the probability that the average wait time is greater than 20 minutes? (Hint: Round the probability value to 2 decimal places. )
A)0.28
B)0.16
C)0.09
D)0.03
A)0.28
B)0.16
C)0.09
D)0.03

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
21
If the sample size,n,equals the population size,N,then the variance of the sample mean, 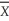
,is zero.
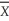
,is zero.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
22
Based on the sampling distribution of the means and the central limit theorem,the sample mean can be used as a good estimator of the population mean,assuming that the sample size,n,is sufficiently large.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
23
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
Suppose that 20% of all invoices are for amounts greater than $800.A random sample of 50 invoices is taken.
Based on the central limit theorem,the mean of all possible sample means is equal to the population:
A)variance.
B)mean.
C)median.
D)standard deviation.
Suppose that 20% of all invoices are for amounts greater than $800.A random sample of 50 invoices is taken.
Based on the central limit theorem,the mean of all possible sample means is equal to the population:
A)variance.
B)mean.
C)median.
D)standard deviation.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
24
All possible random samples of 200 middle managers are selected from a population for a study concerning their mean annual income.The population standard deviation is computed to be $2,248.5.What is the standard deviation of the sampling distribution of the means?
A)$47.42
B)$11.24
C)$158.99
D)$57.86
A)$47.42
B)$11.24
C)$158.99
D)$57.86

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
25
A basketball player shoots 60 free throws a day and historically makes 75 percent of them.What is the probability that he will make at most 80 percent tomorrow?
A)0.1056
B)0.8133
C)0.1867
D)0.8944
A)0.1056
B)0.8133
C)0.1867
D)0.8944

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
26
Random samples of size 36 each are taken from a large population whose mean is 120 and standard deviation is 39.The standard error of the sampling distribution of sample mean is:
A)39
B)6.5
C)15.6
D)24.5
A)39
B)6.5
C)15.6
D)24.5

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
27
As the size of the sample increases,what happens to the shape of the sampling distribution of sample means?
A)It becomes positively skewed.
B)It becomes negatively skewed.
C)It becomes uniformly distributed.
D)It becomes approximately normal.
A)It becomes positively skewed.
B)It becomes negatively skewed.
C)It becomes uniformly distributed.
D)It becomes approximately normal.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
28
If the standard error of the sampling distribution of the sample proportion is 0.02049 for samples of size 500,then the population proportion must be either:
A)0.2 or 0.8
B)0.5 or 0.5
C)0.3 or 0.7
D)0.6 or 0.4
A)0.2 or 0.8
B)0.5 or 0.5
C)0.3 or 0.7
D)0.6 or 0.4

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
29
A golfer practices 60 twenty-foot putts a day and historically makes 25 percent of them.Calculate the standard error of the sample proportion.
A)0.3256
B)0.6258
C)0.0559
D)0.4057
A)0.3256
B)0.6258
C)0.0559
D)0.4057

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
30
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
Suppose that 20% of all invoices are for amounts greater than $800.A random sample of 50 invoices is taken.
What is the probability that at least 25% of these 50 invoices are for more than $800?
A)0.1894
B)0.8106
C)0.3106
D)0.8894
Suppose that 20% of all invoices are for amounts greater than $800.A random sample of 50 invoices is taken.
What is the probability that at least 25% of these 50 invoices are for more than $800?
A)0.1894
B)0.8106
C)0.3106
D)0.8894

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
31
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
You have recently joined a Weight Watchers club.Suppose that the number of times you expect to visit the club in a month is represented by a normally distributed random variable with a mean of 12 and a standard deviation of 2.50.
The probability is 85% that you average less than how many visits to the club per month over the course of next year?
A)12.75
B)11.50
C)12.50
D)11.75
You have recently joined a Weight Watchers club.Suppose that the number of times you expect to visit the club in a month is represented by a normally distributed random variable with a mean of 12 and a standard deviation of 2.50.
The probability is 85% that you average less than how many visits to the club per month over the course of next year?
A)12.75
B)11.50
C)12.50
D)11.75

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
32
The standard deviation of  is also called the:
is also called the:
A)standard error of the sampling distribution of sample proportions.
B)standard deviation of the population.
C)normal approximation to the binomial.
D)continuity correction factor.
 is also called the:
is also called the:A)standard error of the sampling distribution of sample proportions.
B)standard deviation of the population.
C)normal approximation to the binomial.
D)continuity correction factor.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
33
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
Suppose that 20% of all invoices are for amounts greater than $800.A random sample of 50 invoices is taken.
The average score of all students who took a particular statistics class last semester has a mean of 70 and a standard deviation of 3.0.Suppose 36 students who are taking the class this semester are selected at random.Find the probability that the average score of the 36 students exceeds 71.
A)0.0228
B)0.0772
C)0.1228
D)0.1772.
Suppose that 20% of all invoices are for amounts greater than $800.A random sample of 50 invoices is taken.
The average score of all students who took a particular statistics class last semester has a mean of 70 and a standard deviation of 3.0.Suppose 36 students who are taking the class this semester are selected at random.Find the probability that the average score of the 36 students exceeds 71.
A)0.0228
B)0.0772
C)0.1228
D)0.1772.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
34
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
Suppose that 20% of all invoices are for amounts greater than $800.A random sample of 50 invoices is taken.
Suppose that 15% of all invoices are for amounts greater than $1,000.A random sample of 60 invoices is taken.What is the probability that between 13% and 23% of these 60 invoices are for more than $1,000?
A)0.4591
B)0.2019
C)0.1664
D)0.6255
Suppose that 20% of all invoices are for amounts greater than $800.A random sample of 50 invoices is taken.
Suppose that 15% of all invoices are for amounts greater than $1,000.A random sample of 60 invoices is taken.What is the probability that between 13% and 23% of these 60 invoices are for more than $1,000?
A)0.4591
B)0.2019
C)0.1664
D)0.6255

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
35
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
Suppose that 20% of all invoices are for amounts greater than $800.A random sample of 50 invoices is taken.
What is the mean and standard error of the sample proportion of invoices with amounts in excess of $800?
A)mean = 10,standard error = 0.4472
B)mean = 0.20,standard error = 0.0566
C)mean = 0.20,standard error = 0.0032
D)mean = 10,standard error = 0.0598
Suppose that 20% of all invoices are for amounts greater than $800.A random sample of 50 invoices is taken.
What is the mean and standard error of the sample proportion of invoices with amounts in excess of $800?
A)mean = 10,standard error = 0.4472
B)mean = 0.20,standard error = 0.0566
C)mean = 0.20,standard error = 0.0032
D)mean = 10,standard error = 0.0598

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
36
The variance of the sampling distribution of the sample mean is equal to the variance of the population mean divided by the square root of the sample size.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
37
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
Suppose that 20% of all invoices are for amounts greater than $800.A random sample of 50 invoices is taken.
What is the probability that more than 22.7% of these 50 invoices are for more than $800?
A)0.1368
B)0.2266
C)0.3156
D)0.2734
Suppose that 20% of all invoices are for amounts greater than $800.A random sample of 50 invoices is taken.
What is the probability that more than 22.7% of these 50 invoices are for more than $800?
A)0.1368
B)0.2266
C)0.3156
D)0.2734

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
38
According to the central limit theorem,the sampling distribution of the sample mean can be approximated by the normal distribution as the:
A)number of samples gets large enough.
B)sample size gets large enough.
C)population standard deviation increases.
D)sample standard deviation decreases.
A)number of samples gets large enough.
B)sample size gets large enough.
C)population standard deviation increases.
D)sample standard deviation decreases.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
39
If all possible random samples of size n are taken from a population,and the mean of each sample is determined,the mean of the sample distribution is:
A)larger than the population mean.
B)exactly the same as the population mean.
C)smaller than the population mean.
D)unrelated to the population mean.
A)larger than the population mean.
B)exactly the same as the population mean.
C)smaller than the population mean.
D)unrelated to the population mean.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
40
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
You have recently joined a Weight Watchers club.Suppose that the number of times you expect to visit the club in a month is represented by a normally distributed random variable with a mean of 12 and a standard deviation of 2.50.
Over the course of the next year,what is the probability that you average more than 13 visits to the club?
A)0.1554
B)0.4177
C)0.3446
D)0.0823
You have recently joined a Weight Watchers club.Suppose that the number of times you expect to visit the club in a month is represented by a normally distributed random variable with a mean of 12 and a standard deviation of 2.50.
Over the course of the next year,what is the probability that you average more than 13 visits to the club?
A)0.1554
B)0.4177
C)0.3446
D)0.0823

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
41
The fraction of the population in the sample determines the precision of results from a random sample.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
42
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
Suppose you flip a coin four times.For every head,you receive one point,and for every tail,you lose one point.
What is the probability that the mean number of points you receive on four flips is 0.5?
Suppose you flip a coin four times.For every head,you receive one point,and for every tail,you lose one point.
What is the probability that the mean number of points you receive on four flips is 0.5?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
43
The chi-square family of distributions is used in applied statistical analysis because it provides a link between the sample and population variances.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
44
The mean of the sampling distribution of the sample proportion 
,when the sample size n = 100 and the population proportion P = 0.92,is 92.0

,when the sample size n = 100 and the population proportion P = 0.92,is 92.0

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
45
The central limit theorem is basic to the concept of statistical inference because it permits us to draw conclusions about the population based strictly on sample data.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
46
The variance of the sampling distribution of the sample proportion is equal to P(1 - P)/ n.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
47
The standard error of the mean is also called sampling error.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
48
If a random sample of 250 observations is taken from a population whose proportion P is equal to 0.6,then the expected value of the sample proportion 
is 0.40

is 0.40

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
49
The central limit theorem states that as the sample size increases,the distribution of the population mean approaches the normal distribution.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
50
Acceptance intervals are widely used for quality control monitoring of various production and service processes.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
51
The central limit theorem states that if all possible random samples of size n are taken from any population,the sampling distribution of sample means becomes approximately normal when the sample size n is large enough.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
52
The variance of the sampling distribution of sample mean 
decreases as the sample size,n,increases.

decreases as the sample size,n,increases.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
53
The central limit theorem states that the sampling distribution of sample means will closely resemble the normal distribution regardless of the sample size.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
54
The mean and variance of a chi-square distribution with ν degrees of freedom is determined by the number of degrees of freedom.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
55
The standard error of the sampling distribution of the sample proportion 
,when the sample size n = 100 and the population proportion P = 0.30,is 0.0021

,when the sample size n = 100 and the population proportion P = 0.30,is 0.0021

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
56
If the standard error of the sampling distribution of sample proportions is 0.0245 for samples of size 400,then the population proportion must be 0.40.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
57
The sampling distribution of sample means is normal for samples of any size,n,provided that the parent sampled population has a normal distribution.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
58
The central limit theorem can be applied to both discrete and continuous random variables.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
59
The larger the sample size,the larger the standard error of the sample proportion.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
60
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
Suppose you flip a coin four times.For every head,you receive one point,and for every tail,you lose one point.
Develop the sampling distribution for the mean number of points you receive from flipping four coins.
Suppose you flip a coin four times.For every head,you receive one point,and for every tail,you lose one point.
Develop the sampling distribution for the mean number of points you receive from flipping four coins.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
61
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
You have recently joined a country club.Suppose that the number of times you expect to play golf in a month is represented by a normally distributed random variable with a mean of 10 and a standard deviation of 2.4.
Over the course of the next year,what is the probability that you average more than 11 games a month?
You have recently joined a country club.Suppose that the number of times you expect to play golf in a month is represented by a normally distributed random variable with a mean of 10 and a standard deviation of 2.4.
Over the course of the next year,what is the probability that you average more than 11 games a month?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
62
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
Let the random variable X follow a normal distribution with a mean of μ and a standard deviation of σ.Let
1 be the mean of a sample of 16 observations randomly chosen from this population,and
2 be the mean of a sample of 25 observations randomly chosen from the same population.
Suppose that 15% of all invoices are for amounts greater than $1,000.A random sample of 60 invoices is taken.What is the mean and standard error of the sample proportion of invoices with amounts in excess of $1,000? What is the probability that the proportion of invoices in the sample is greater than 18%?
Let the random variable X follow a normal distribution with a mean of μ and a standard deviation of σ.Let

1 be the mean of a sample of 16 observations randomly chosen from this population,and

2 be the mean of a sample of 25 observations randomly chosen from the same population.
Suppose that 15% of all invoices are for amounts greater than $1,000.A random sample of 60 invoices is taken.What is the mean and standard error of the sample proportion of invoices with amounts in excess of $1,000? What is the probability that the proportion of invoices in the sample is greater than 18%?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
63
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
In a recent survey of high school students,it was found that the average amount of money spent on entertainment each week was normally distributed with a mean of $52.30 and a standard deviation of $18.23.Assume that these values are representative of all high school students.
The probability is 65% that the average spending of a sample of 25 randomly-selected students will spend at least how much?
In a recent survey of high school students,it was found that the average amount of money spent on entertainment each week was normally distributed with a mean of $52.30 and a standard deviation of $18.23.Assume that these values are representative of all high school students.
The probability is 65% that the average spending of a sample of 25 randomly-selected students will spend at least how much?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
64
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
The length of time it takes to fill an order at a local sandwich shop is normally distributed with a mean of 4.1 minutes and a standard deviation of 1.3 minutes.
The probability is 95% that the average waiting time for a random sample of ten customers is greater than how many minutes?
The length of time it takes to fill an order at a local sandwich shop is normally distributed with a mean of 4.1 minutes and a standard deviation of 1.3 minutes.
The probability is 95% that the average waiting time for a random sample of ten customers is greater than how many minutes?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
65
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
It has been found that 62.1% of all unsolicited third class mail delivered to households goes unread.Over the course of a month,a household receives 100 pieces of unsolicited mail.
What is the probability that the sample proportion is greater than 0.60?
It has been found that 62.1% of all unsolicited third class mail delivered to households goes unread.Over the course of a month,a household receives 100 pieces of unsolicited mail.
What is the probability that the sample proportion is greater than 0.60?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
66
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
A sample of 25 bottles is taken from the production line at a local bottling plant.Assume that the fill amounts follow a normal distribution.
What is the probability that the sample standard deviation is more than 70% of the population standard deviation?
A sample of 25 bottles is taken from the production line at a local bottling plant.Assume that the fill amounts follow a normal distribution.
What is the probability that the sample standard deviation is more than 70% of the population standard deviation?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
67
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
Let the random variable X follow a normal distribution with a mean of μ and a standard deviation of σ.Let
1 be the mean of a sample of 16 observations randomly chosen from this population,and
2 be the mean of a sample of 25 observations randomly chosen from the same population.
Evaluate the statement P
1 < μ +
)< P(
2 < μ +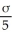
)as to whether it is true or false.Please state if you are unable to determine whether the statement is true or false.Support your answer.
Let the random variable X follow a normal distribution with a mean of μ and a standard deviation of σ.Let

1 be the mean of a sample of 16 observations randomly chosen from this population,and

2 be the mean of a sample of 25 observations randomly chosen from the same population.
Evaluate the statement P

1 < μ +

)< P(

2 < μ +
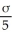
)as to whether it is true or false.Please state if you are unable to determine whether the statement is true or false.Support your answer.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
68
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
It has been found that 62.1% of all unsolicited third class mail delivered to households goes unread.Over the course of a month,a household receives 100 pieces of unsolicited mail.
What is the variance of the proportion?
It has been found that 62.1% of all unsolicited third class mail delivered to households goes unread.Over the course of a month,a household receives 100 pieces of unsolicited mail.
What is the variance of the proportion?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
69
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
In a recent survey of high school students,it was found that the average amount of money spent on entertainment each week was normally distributed with a mean of $52.30 and a standard deviation of $18.23.Assume that these values are representative of all high school students.
What is the probability that for a sample of 25,the average amount spent exceeds $60?
In a recent survey of high school students,it was found that the average amount of money spent on entertainment each week was normally distributed with a mean of $52.30 and a standard deviation of $18.23.Assume that these values are representative of all high school students.
What is the probability that for a sample of 25,the average amount spent exceeds $60?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
70
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
A sample of 25 bottles is taken from the production line at a local bottling plant.Assume that the fill amounts follow a normal distribution.
The probability is 90% that the sample variance is less than what percent of the population variance?
A sample of 25 bottles is taken from the production line at a local bottling plant.Assume that the fill amounts follow a normal distribution.
The probability is 90% that the sample variance is less than what percent of the population variance?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
71
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
The length of time it takes to fill an order at a local sandwich shop is normally distributed with a mean of 4.1 minutes and a standard deviation of 1.3 minutes.
What is the probability that the average waiting time for a random sample of ten customers is between 4.0 and 4.2 minutes?
The length of time it takes to fill an order at a local sandwich shop is normally distributed with a mean of 4.1 minutes and a standard deviation of 1.3 minutes.
What is the probability that the average waiting time for a random sample of ten customers is between 4.0 and 4.2 minutes?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
72
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
It has been found that 62.1% of all unsolicited third class mail delivered to households goes unread.Over the course of a month,a household receives 100 pieces of unsolicited mail.
What is the standard error of the sample proportion?
It has been found that 62.1% of all unsolicited third class mail delivered to households goes unread.Over the course of a month,a household receives 100 pieces of unsolicited mail.
What is the standard error of the sample proportion?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
73
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
It has been found that 62.1% of all unsolicited third class mail delivered to households goes unread.Over the course of a month,a household receives 100 pieces of unsolicited mail.
What is the mean of the sample proportion of pieces of unread mail?
It has been found that 62.1% of all unsolicited third class mail delivered to households goes unread.Over the course of a month,a household receives 100 pieces of unsolicited mail.
What is the mean of the sample proportion of pieces of unread mail?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
74
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
The filling machine at a bottling plant is operating correctly when the variance of the fill amount is equal to 0.3 ounces.Assume that the fill amounts follow a normal distribution.
The probability is 0.10 that for a sample of 30 bottles,the sample variance is less than what number?
The filling machine at a bottling plant is operating correctly when the variance of the fill amount is equal to 0.3 ounces.Assume that the fill amounts follow a normal distribution.
The probability is 0.10 that for a sample of 30 bottles,the sample variance is less than what number?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
75
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
Suppose you flip a coin four times.For every head,you receive one point,and for every tail,you lose one point.
What is the probability that the mean number of points you receive on four flips is 0?
Suppose you flip a coin four times.For every head,you receive one point,and for every tail,you lose one point.
What is the probability that the mean number of points you receive on four flips is 0?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
76
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
Let the random variable X follow a normal distribution with a mean of μ and a standard deviation of σ.Let
1 be the mean of a sample of 16 observations randomly chosen from this population,and
2 be the mean of a sample of 25 observations randomly chosen from the same population.
Evaluate the statement P(
1 < μ +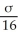
)< P(
2 < μ +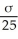
)as to whether it is true or false.Please state if you are unable to determine whether the statement is true or false.Support your answer.
Let the random variable X follow a normal distribution with a mean of μ and a standard deviation of σ.Let

1 be the mean of a sample of 16 observations randomly chosen from this population,and

2 be the mean of a sample of 25 observations randomly chosen from the same population.
Evaluate the statement P(

1 < μ +
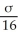
)< P(

2 < μ +
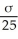
)as to whether it is true or false.Please state if you are unable to determine whether the statement is true or false.Support your answer.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
77
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
You have recently joined a country club.Suppose that the number of times you expect to play golf in a month is represented by a normally distributed random variable with a mean of 10 and a standard deviation of 2.4.
The number of orders that come into a mail-order sales office each month is normally distributed with a mean of 298 and a standard deviation of 15.4.For a particular sample size,the probability that the sample mean exceeds 300 is 0.2.How big must the sample be?
You have recently joined a country club.Suppose that the number of times you expect to play golf in a month is represented by a normally distributed random variable with a mean of 10 and a standard deviation of 2.4.
The number of orders that come into a mail-order sales office each month is normally distributed with a mean of 298 and a standard deviation of 15.4.For a particular sample size,the probability that the sample mean exceeds 300 is 0.2.How big must the sample be?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
78
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
You have recently joined a country club.Suppose that the number of times you expect to play golf in a month is represented by a normally distributed random variable with a mean of 10 and a standard deviation of 2.4.
Over the course of the next year,the probability is 85% that you average less than how many games per month?
You have recently joined a country club.Suppose that the number of times you expect to play golf in a month is represented by a normally distributed random variable with a mean of 10 and a standard deviation of 2.4.
Over the course of the next year,the probability is 85% that you average less than how many games per month?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
79
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
The filling machine at a bottling plant is operating correctly when the variance of the fill amount is equal to 0.3 ounces.Assume that the fill amounts follow a normal distribution.
What is the probability that for a sample of 30 bottles,the sample variance is greater than 0.5?
The filling machine at a bottling plant is operating correctly when the variance of the fill amount is equal to 0.3 ounces.Assume that the fill amounts follow a normal distribution.
What is the probability that for a sample of 30 bottles,the sample variance is greater than 0.5?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
80
THE NEXT QUESTIONS ARE BASED ON THE FOLLOWING INFORMATION:
Let the random variable X follow a normal distribution with a mean of μ and a standard deviation of σ.Let
1 be the mean of a sample of 16 observations randomly chosen from this population,and
2 be the mean of a sample of 25 observations randomly chosen from the same population.
Evaluate the statement P(μ - 0.2σ <
1 < μ + 0.2σ)< P(μ - 0.2σ <
2 < μ + 0.2σ)as to whether it is true or false.Please state if you are unable to determine whether the statement is true or false.Support your answer.
Let the random variable X follow a normal distribution with a mean of μ and a standard deviation of σ.Let

1 be the mean of a sample of 16 observations randomly chosen from this population,and

2 be the mean of a sample of 25 observations randomly chosen from the same population.
Evaluate the statement P(μ - 0.2σ <

1 < μ + 0.2σ)< P(μ - 0.2σ <

2 < μ + 0.2σ)as to whether it is true or false.Please state if you are unable to determine whether the statement is true or false.Support your answer.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck


