Deck 12: Hypothesis Testing for Two Populations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/72
Play
Full screen (f)
Deck 12: Hypothesis Testing for Two Populations
1
A researcher wants to conduct a before/after study on 11 subjects to determine if a new cholesterol medication results in higher HDL cholesterol readings. The null hypothesis is that the average difference is zero while the alternative hypothesis is that the average difference is zero. Scores are obtained on the subjects both before and after taking the medication. After subtracting the after scores from the before scores, the average difference is computed to be -2.40 with a sample standard deviation of 1.21. A 0.05 level of significance is selected. Assume that the differences are normally distributed in the population. The table t value for this test is ___.
A) 1.812
B) 2.228
C) 2.086
D) 2.262
E) 3.2467
A) 1.812
B) 2.228
C) 2.086
D) 2.262
E) 3.2467
2.228
2
If the populations are normally distributed but the population variances are unknown the t statistic can be used as the basis for statistical inferences about the difference in two population means using two independent random samples.
True
3
To determine if there is a difference in the speed of a wireless router from two different manufacturers, a network manager will draw independent samples of wireless routers from the two manufacturers and compare the difference in the sample means for the connection speed.
True
4
A researcher is conducting a matched?pairs study. She gathers data on each pair in the study resulting in: 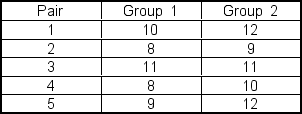 Assume that the data are normally distributed in the population. The degrees of freedom in this problem are ___.
Assume that the data are normally distributed in the population. The degrees of freedom in this problem are ___.
A) 4
B) 8
C) 5
D) 9
E) 3
 Assume that the data are normally distributed in the population. The degrees of freedom in this problem are ___.
Assume that the data are normally distributed in the population. The degrees of freedom in this problem are ___.A) 4
B) 8
C) 5
D) 9
E) 3

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
5
When testing for the difference between two population proportions, we use the "pooled" estimate of the proportion.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
6
If the populations are normally distributed and the variances of the two populations are equal, it is appropriate to use the "pooled" formula to determine the t statistic for the hypothesis test of the difference in the two population means.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
7
Sets of matched samples are also referred to as dependent samples.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
8
Hypothesis tests conducted on sets of matched samples are sometimes referred to as correlated t tests.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
9
If the populations are normally distributed but the population variances are unknown the z statistic can be used as the basis for statistical inferences about the difference in two population means using two independent random samples.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
10
If the variances of the two populations are equal, it is appropriate to use the "pooled" formula to determine the t statistic for the hypothesis test of the difference in the two population means.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
11
The difference in two sample means is normally distributed for sample sizes ≥ 30, only if the populations are normally distributed.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
12
If the populations are normally distributed and the variances of the two populations are equal, it is appropriate to use the "unpooled" formula to determine the t statistic for the hypothesis test of the difference in the two population means.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
13
A researcher wants to conduct a before/after study on 11 subjects to determine if a new cholesterol medication results in higher HDL cholesterol readings. The null hypothesis is that the average difference is zero while the alternative hypothesis is that the average difference is zero. Scores are obtained on the subjects both before and after taking the medication. After subtracting the after scores from the before scores, the average difference is computed to be -2.40 with a sample standard deviation of 1.21. Assume that the differences are normally distributed in the population. The degrees of freedom for this test are ___.
A) 11
B) 10
C) 9
D) 20
E) 2
A) 11
B) 10
C) 9
D) 20
E) 2

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
14
In a set of matched samples, each data value in one sample is related to or matched with a corresponding data value in the other sample.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
15
A researcher wants to conduct a before/after study on 11 subjects to determine if a new cholesterol medication results in higher HDL cholesterol readings. The null hypothesis is that the average difference is zero while the alternative hypothesis is that the average difference is zero. Scores are obtained on the subjects both before and after taking the medication. After subtracting the after scores from the before scores, the average difference is computed to be -2.40 with a sample standard deviation of 1.21. Assume that the differences are normally distributed in the population. The observed t value for this test is ___.
A) -21.82
B) -6.58
C) -2.4
D) 1.98
E) 2.33
A) -21.82
B) -6.58
C) -2.4
D) 1.98
E) 2.33

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
16
In conducting a matched-pairs hypothesis test, the null and alternative hypotheses always represent one-tailed tests.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
17
If the sample sizes are small, but the populations are normally distributed and the population variances are known, the z statistic can be used as the basis for statistical inferences about the difference in two population means using two independent random samples.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
18
A researcher is conducting a matched?pairs study. She gathers data on each pair in the study resulting in: 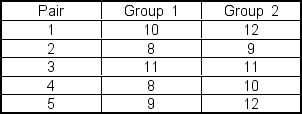 Assume that the data are normally distributed in the population. The level of significance is selected to be 0.10. If a two-tailed test is performed, the null hypothesis would be rejected if the observed value of t is ___.
Assume that the data are normally distributed in the population. The level of significance is selected to be 0.10. If a two-tailed test is performed, the null hypothesis would be rejected if the observed value of t is ___.
A) less than -1.533 or greater than 1.533
B) less than -2.132 or greater than 2.132
C) less than -2.776 or greater than 2.776
D) less than -1.860 or greater than 1.860
E) less than -2.000 or greater than 2.000
 Assume that the data are normally distributed in the population. The level of significance is selected to be 0.10. If a two-tailed test is performed, the null hypothesis would be rejected if the observed value of t is ___.
Assume that the data are normally distributed in the population. The level of significance is selected to be 0.10. If a two-tailed test is performed, the null hypothesis would be rejected if the observed value of t is ___.A) less than -1.533 or greater than 1.533
B) less than -2.132 or greater than 2.132
C) less than -2.776 or greater than 2.776
D) less than -1.860 or greater than 1.860
E) less than -2.000 or greater than 2.000

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
19
A researcher is conducting a matched?pairs study. She gathers data on each pair in the study resulting in: 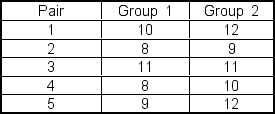 Assume that the data are normally distributed in the population. The sample standard deviation (sd) of the differences is ___.
Assume that the data are normally distributed in the population. The sample standard deviation (sd) of the differences is ___.
A) 1.3
B) 1.14
C) 1.04
D) 1.02
E) 1.47
 Assume that the data are normally distributed in the population. The sample standard deviation (sd) of the differences is ___.
Assume that the data are normally distributed in the population. The sample standard deviation (sd) of the differences is ___.A) 1.3
B) 1.14
C) 1.04
D) 1.02
E) 1.47

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
20
If the sample sizes are greater than 30 and the population variances are known, the basis for statistical inferences about the difference in two population means using two independent random samples is the z statistic, regardless of the shapes of the population distributions.

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
21
A researcher is interested in testing to determine if the mean price of a casual lunch is different in the city than it is in the suburbs. The null hypothesis is that there is no difference in the population means (i.e., the difference is zero). The alternative hypothesis is that there is a difference (i.e., the difference is equal to zero). He randomly selects a sample of 9 lunch tickets from the city population resulting in a mean of $14.30 and a standard deviation of $3.40. He randomly selects a sample of 14 lunch tickets from the suburban population resulting in a mean of $11.80 and a standard deviation $2.90. He is using an alpha value of.10 to conduct this test. Assuming that the populations are normally distributed, the critical t value from the table is ___.
A) 1.323
B) 1.721
C) 1.717
D) 1.321
E) 2.321
A) 1.323
B) 1.721
C) 1.717
D) 1.321
E) 2.321

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
22
Golf course designer Roberto Langabeer is evaluating two sites, Palmetto Dunes and Ocean Greens, for his next golf course. He wants to prove that Palmetto Dunes residents (population 1) play golf more often than Ocean Greens residents (population 2). Roberto commissions a market survey to test this hypothesis. The market researcher used a random sample of 64 individuals from each suburb, and reported the following:  1 = 15 times per month and
1 = 15 times per month and 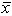
2 = 14 times per month. Assume that 1 = 2 and 2 = 3. With =.01, the critical z value is ___.
A) -1.96
B) 1.96
C) -2.33
D) -1.33
E) 2.33
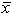 1 = 15 times per month and
1 = 15 times per month and 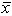
2 = 14 times per month. Assume that 1 = 2 and 2 = 3. With =.01, the critical z value is ___.
A) -1.96
B) 1.96
C) -2.33
D) -1.33
E) 2.33

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
23
Golf course designer Roberto Langabeer is evaluating two sites, Palmetto Dunes and Ocean Greens, for his next golf course. He wants to prove that Palmetto Dunes residents (population 1) play golf more often than Ocean Greens residents (population 2). Roberto commissions a market survey to test this hypothesis. The market researcher used a random sample of 64 individuals from each suburb, and reported the following: 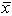 1 = 15 times per month and
1 = 15 times per month and 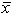
2 = 14 times per month. Assume that 1 = 2 and 2 = 3. With =.01, the observed z value is ___.
A) 2.22
B) 12.81
C) 4.92
D) 3.58
E) 1.96
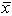 1 = 15 times per month and
1 = 15 times per month and 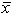
2 = 14 times per month. Assume that 1 = 2 and 2 = 3. With =.01, the observed z value is ___.
A) 2.22
B) 12.81
C) 4.92
D) 3.58
E) 1.96

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
24
A researcher is estimating the average difference between two population means based on matched?pairs samples. She gathers data on each pair in the study resulting in: 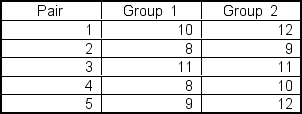 Assume that the data are normally distributed in the population. To obtain a 95% confidence interval, the table t value would be ___.
Assume that the data are normally distributed in the population. To obtain a 95% confidence interval, the table t value would be ___.
A) 2.132
B) 1.86
C) 2.306
D) 2.976
E) 2.776
 Assume that the data are normally distributed in the population. To obtain a 95% confidence interval, the table t value would be ___.
Assume that the data are normally distributed in the population. To obtain a 95% confidence interval, the table t value would be ___.A) 2.132
B) 1.86
C) 2.306
D) 2.976
E) 2.776

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
25
Lucy Baker is analyzing demographic characteristics of two television programs, American Idol (population 1) and 60 Minutes (population 2). Previous studies indicate no difference in the ages of the two audiences. (The mean age of each audience is the same.) Her staff randomly selected 100 people from each audience, and reported the following: 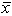 1 = 43 years and
1 = 43 years and 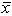
2 = 45 years. Assume that 1 = 5 and 2 = 8. Assuming a two-tail test and =.05, the observed z value is ___.
A) -2.12
B) -2.25
C) -5.58
D) -15.38
E) -20.68
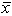 1 = 43 years and
1 = 43 years and 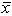
2 = 45 years. Assume that 1 = 5 and 2 = 8. Assuming a two-tail test and =.05, the observed z value is ___.
A) -2.12
B) -2.25
C) -5.58
D) -15.38
E) -20.68

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
26
Lucy Baker is analyzing demographic characteristics of two television programs, American Idol (population 1) and 60 Minutes (population 2). Previous studies indicate no difference in the ages of the two audiences. (The mean age of each audience is the same.) Lucy plans to test this hypothesis using a random sample of 100 from each audience. Her alternate hypothesis is ___.
A) 1 - 2 ≤ 0
B) 1 - 2 ≥ 0
C) 1 - 2 = 0
D) 1 - 2
E) 1 - 2 = 1
A) 1 - 2 ≤ 0
B) 1 - 2 ≥ 0
C) 1 - 2 = 0
D) 1 - 2
E) 1 - 2 = 1

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
27
Golf course designer Roberto Langabeer is evaluating two sites, Palmetto Dunes and Ocean Greens, for his next golf course. He wants to prove that Palmetto Dunes residents (population 1) play golf more often than Ocean Greens residents (population 2). Roberto plans to test this hypothesis using a random sample of 81 individuals from each suburb. His null hypothesis is ___.
A)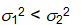
B)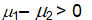
C)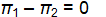
D)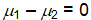
E)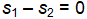
A)
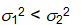
B)
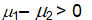
C)
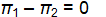
D)
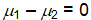
E)
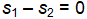

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
28
Golf course designer Roberto Langabeer is evaluating two sites, Palmetto Dunes and Ocean Greens, for his next golf course. He wants to prove that Palmetto Dunes residents (population 1) play golf more often than Ocean Greens residents (population 2). Roberto plans to test this hypothesis using a random sample of 81 individuals from each suburb. His null hypothesis is ___.
A)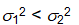
B)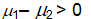
C)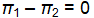
D)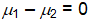
E)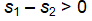
A)
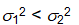
B)
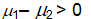
C)
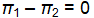
D)
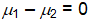
E)
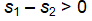

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
29
You are evaluating investing in a cognitive training company. For this reason, you want to determine whether users who complete at least 75% of the recommended daily training for two months show improved levels of reading comprehension and problem solving skills. You select a random sample of new users and get test scores for each participant in the sample. The test score is a composite of reading comprehension and problem solving skills. Two months later, you randomly select 15 users who have completed 75% or more of the recommended training for the last two months and have them take a test similar to the initial test. You are interested in determining whether the average test score before training is different than the average test score after training for this sample. The after-training average is 92.8, which is 2.7 points higher than the before-training average. The sample standard deviations of the differences is 1.2. You can assume that the differences are normally distributed in the population. The degrees of freedom for this test are ___.
A) 30
B) 29
C) 28
D) 15
E) 14
A) 30
B) 29
C) 28
D) 15
E) 14

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
30
Lucy Baker is analyzing demographic characteristics of two television programs, American Idol (population 1) and 60 Minutes (population 2). Previous studies indicate no difference in the ages of the two audiences. (The mean age of each audience is the same.) Lucy plans to test this hypothesis using a random sample of 100 from each audience. Her null hypothesis is ___.
A) 1 - 2 0
B) 1 - 2 ≥ 0
C) 1 - 2 = 0
D) 1 - 2 ≤ 0
E) 1 - 2 ≤ 1
A) 1 - 2 0
B) 1 - 2 ≥ 0
C) 1 - 2 = 0
D) 1 - 2 ≤ 0
E) 1 - 2 ≤ 1

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
31
Golf course designer Roberto Langabeer is evaluating two sites, Palmetto Dunes and Ocean Greens, for his next golf course. He wants to prove that Palmetto Dunes residents (population 1) play golf more often than Ocean Greens residents (population 2). Roberto commissions a market survey to test this hypothesis. The market researcher used a random sample of 64 individuals from each suburb, and reported the following: 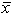 1 = 15 times per month and
1 = 15 times per month and 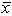
2 = 14 times per month. Assume that 1 = 2 and 2 = 3. With =.01, the appropriate decision is ___.
A) reject the null hypothesis 12 < 22
B) accept the alternate hypothesis 1 - 2 > 0
C) reject the alternate hypothesis n1 = n2 = 64
D) fail to reject the null hypothesis 1 - 2 > 0
E) do nothing
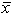 1 = 15 times per month and
1 = 15 times per month and 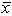
2 = 14 times per month. Assume that 1 = 2 and 2 = 3. With =.01, the appropriate decision is ___.
A) reject the null hypothesis 12 < 22
B) accept the alternate hypothesis 1 - 2 > 0
C) reject the alternate hypothesis n1 = n2 = 64
D) fail to reject the null hypothesis 1 - 2 > 0
E) do nothing

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
32
A researcher is interested in testing to determine if the mean price of a casual lunch is different in the city than it is in the suburbs. The null hypothesis is that there is no difference in the population means (i.e., the difference is zero). The alternative hypothesis is that there is a difference (i.e., the difference is equal to zero). He randomly selects a sample of 9 lunch tickets from the city population resulting in a mean of $14.30 and a standard deviation of $3.40. He randomly selects a sample of 14 lunch tickets from the suburban population resulting in a mean of $11.80 and a standard deviation $2.90. He is using an alpha value of.10 to conduct this test. Assuming that the populations are normally distributed and that the population variances are approximately equal, the degrees of freedom for this problem are ___.
A) 23
B) 22
C) 21
D) 1
E) 2
A) 23
B) 22
C) 21
D) 1
E) 2

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
33
Lucy Baker is analyzing demographic characteristics of two television programs, American Idol (population 1) and 60 Minutes (population 2). Previous studies indicate no difference in the ages of the two audiences. (The mean age of each audience is the same.) Her staff randomly selected 100 people from each audience, and reported the following: 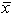 1 = 43 years and
1 = 43 years and 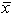
2 = 45 years. Assume that 1 = 5 and 2 = 8. With a two-tail test and =.05, the appropriate decision is ___.
A) do not reject the null hypothesis 1 - 2 = 0
B) reject the null hypothesis 1 - 2 ≥ 0
C) reject the null hypothesis 1 - 2 = 0
D) do not reject the null hypothesis 1 - 2 ≤ 0
E) do nothing
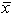 1 = 43 years and
1 = 43 years and 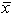
2 = 45 years. Assume that 1 = 5 and 2 = 8. With a two-tail test and =.05, the appropriate decision is ___.
A) do not reject the null hypothesis 1 - 2 = 0
B) reject the null hypothesis 1 - 2 ≥ 0
C) reject the null hypothesis 1 - 2 = 0
D) do not reject the null hypothesis 1 - 2 ≤ 0
E) do nothing

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
34
A researcher is conducting a matched?pairs study. She gathers data on each pair in the study resulting in: 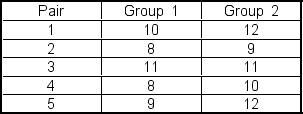 Assume that the data are normally distributed in the population. The level of significance is selected to be 0.10. If the alternative hypothesis is that the average difference is greater than zero, the null hypothesis would be rejected if the observed value of t is ___.
Assume that the data are normally distributed in the population. The level of significance is selected to be 0.10. If the alternative hypothesis is that the average difference is greater than zero, the null hypothesis would be rejected if the observed value of t is ___.
A) greater than 1.533
B) less than -1.533
C) greater than 2.132
D) less than -2.132
E) equal to 2.333
 Assume that the data are normally distributed in the population. The level of significance is selected to be 0.10. If the alternative hypothesis is that the average difference is greater than zero, the null hypothesis would be rejected if the observed value of t is ___.
Assume that the data are normally distributed in the population. The level of significance is selected to be 0.10. If the alternative hypothesis is that the average difference is greater than zero, the null hypothesis would be rejected if the observed value of t is ___.A) greater than 1.533
B) less than -1.533
C) greater than 2.132
D) less than -2.132
E) equal to 2.333

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
35
Lucy Baker is analyzing demographic characteristics of two television programs, American Idol (population 1) and 60 Minutes (population 2). Previous studies indicate no difference in the ages of the two audiences. (The mean age of each audience is the same.) Her staff randomly selected 100 people from each audience, and reported the following:  1 = 43 years and
1 = 43 years and 
2 = 45 years. Assume that 1 = 5 and 2 = 8. With a two-tail test and =.05, the critical z values are ___.
A) -1.64 and 1.64
B) -1.96 and 1.96
C) -2.33 and 2.33
D) -2.58 and 2.58
E) -2.97 and 2.97
 1 = 43 years and
1 = 43 years and 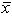
2 = 45 years. Assume that 1 = 5 and 2 = 8. With a two-tail test and =.05, the critical z values are ___.
A) -1.64 and 1.64
B) -1.96 and 1.96
C) -2.33 and 2.33
D) -2.58 and 2.58
E) -2.97 and 2.97

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
36
Golf course designer Roberto Langabeer is evaluating two sites, Palmetto Dunes and Ocean Greens, for his next golf course. He wants to prove that Palmetto Dunes residents (population 1) play golf more often than Ocean Greens residents (population 2). Roberto commissions a market survey to test this hypothesis. The market researcher used a random sample of individuals from each suburb, and reported the following: 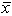 1 = 16 times per month and
1 = 16 times per month and 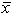
2 = 14 times per month. Assume that 1 = 4 and 2 = 3. With =.01, the appropriate decision is ___.
A) do nothing
B) reject the null hypothesis 1 < 2
C) accept the alternate hypothesis 1 - 2 < 0
D) reject the alternate hypothesis n1 = n2 = 64
E) do not reject the null hypothesis 1 - 2 = 0
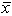 1 = 16 times per month and
1 = 16 times per month and 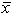
2 = 14 times per month. Assume that 1 = 4 and 2 = 3. With =.01, the appropriate decision is ___.
A) do nothing
B) reject the null hypothesis 1 < 2
C) accept the alternate hypothesis 1 - 2 < 0
D) reject the alternate hypothesis n1 = n2 = 64
E) do not reject the null hypothesis 1 - 2 = 0

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
37
You are evaluating investing in a cognitive training company. For this reason, you want to determine whether users who complete at least 75% of the recommended daily training for two months show improved levels of reading comprehension and problem solving skills. You select a random sample of new users and get test scores for each participant in the sample. The test score is a composite of reading comprehension and problem solving skills. Two months later, you randomly select 15 users who have completed 75% or more of the recommended training for the last two months and have them take a test similar to the initial test. You are interested in determining whether the average test score before training is different than the average test score after training for this sample. The after-training average is 92.8, which is 2.7 points higher than the before-training average. The sample standard deviations of the differences is 1.2. You can assume that the differences are normally distributed in the population. The observed t value for this test is ___.
A) 7.26
B) 8.71
C) 9.55
D) 9.81
E) 33.75
A) 7.26
B) 8.71
C) 9.55
D) 9.81
E) 33.75

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
38
Golf course designer Roberto Langabeer is evaluating two sites, Palmetto Dunes and Ocean Greens, for his next golf course. He wants to prove that Palmetto Dunes residents (population 1) play golf more often than Ocean Greens residents (population 2). Roberto commissions a market survey to test this hypothesis. The market researcher used a random sample of 64 individuals from each suburb, and reported the following: 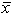 1 = 16 times per month and
1 = 16 times per month and 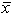
2 = 14 times per month. Assume that 1 = 4 and 2 = 3. With =.01, the observed z value is ___.
A) 18.29
B) 6.05
C) 5.12
D) 3.40
E) 3.20
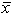 1 = 16 times per month and
1 = 16 times per month and 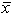
2 = 14 times per month. Assume that 1 = 4 and 2 = 3. With =.01, the observed z value is ___.
A) 18.29
B) 6.05
C) 5.12
D) 3.40
E) 3.20

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
39
A researcher is estimating the average difference between two population means based on matched?pairs samples. She gathers data on each pair in the study resulting in: 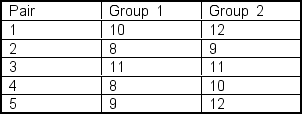 Assume that the data are normally distributed in the population. To obtain a 90% confidence interval, the table t value would be ___.
Assume that the data are normally distributed in the population. To obtain a 90% confidence interval, the table t value would be ___.
A) 1.86
B) 1.397
C) 1.533
D) 2.132
E) 3.346
 Assume that the data are normally distributed in the population. To obtain a 90% confidence interval, the table t value would be ___.
Assume that the data are normally distributed in the population. To obtain a 90% confidence interval, the table t value would be ___.A) 1.86
B) 1.397
C) 1.533
D) 2.132
E) 3.346

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
40
You are evaluating investing in a cognitive training company. For this reason, you want to determine whether users who complete at least 75% of the recommended daily training for two months show improved levels of reading comprehension and problem solving skills. You select a random sample of new users and get test scores for each participant in the sample. The test score is a composite of reading comprehension and problem solving skills. Two months later, you randomly select 15 users who have completed 75% or more of the recommended training for the last two months and have them take a test similar to the initial test. You are interested in determining whether the average test score before training is different than the average test score after training for this sample. The after-training average is 92.8, which is 2.7 points higher than the before-training average. The sample standard deviations of the differences is 1.2. You use a significance level of 0.10, and you can assume that the differences are normally distributed in the population. The table t value for this test is ___.
A) 1.761
B) 1.746
C) 1.753
D) 1.345
E) 1.339
A) 1.761
B) 1.746
C) 1.753
D) 1.345
E) 1.339

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
41
Maureen McIlvoy, owner and CEO of a mail order business for wind surfing equipment and supplies, is reviewing the order filling operations at her warehouses. Her goal is 100% of orders shipped within 24 hours. In previous years, neither warehouse has achieved the goal, but the East Coast Warehouse has consistently out-performed the West Coast Warehouse. Her staff randomly selected 200 orders from the West Coast Warehouse (population 1) and 400 orders from the East Coast Warehouse (population 2), and reports that 190 of the West Coast Orders were shipped within 24 hours, and the East Coast Warehouse shipped 356 orders within 24 hours. Assuming = 0.05, the appropriate decision is ___.
A) reject the null hypothesis π1 - π2 = 0
B) reject the null hypothesis 1 - 2 ≤ 0
C) do not reject the null hypothesis 1 - 2 = 0
D) do not reject the null hypothesis π1 - π2 = 0
E) do not reject the null hypothesis π1 - π2 ≥ 0
A) reject the null hypothesis π1 - π2 = 0
B) reject the null hypothesis 1 - 2 ≤ 0
C) do not reject the null hypothesis 1 - 2 = 0
D) do not reject the null hypothesis π1 - π2 = 0
E) do not reject the null hypothesis π1 - π2 ≥ 0

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
42
Maureen McIlvoy, owner and CEO of a mail order business for wind surfing equipment and supplies, is reviewing the order filling operations at her warehouses. Her goal is 100% of orders shipped within 24 hours. In previous years, neither warehouse has achieved the goal, but the East Coast Warehouse has consistently out-performed the West Coast Warehouse. Her staff randomly selected 200 orders from the West Coast Warehouse (population 1) and 400 orders from the East Coast Warehouse (population 2), and reports that 190 of the West Coast Orders were shipped within 24 hours, and the East Coast Warehouse shipped 372 orders within 24 hours. Assuming = 0.05, the critical z value is ___.
A) -1.96
B) -1.64
C) 1.64
D) 1.96
E) 2.33
A) -1.96
B) -1.64
C) 1.64
D) 1.96
E) 2.33

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
43
Your company is evaluating two cloud-based, secured data storage services. "Pie in the Sky," the newer service, claims its uploading and downloading speeds are faster than the older service, "Cloudy but Steady Skies." You need to make a decision based on published access times for both services at different times and for varying file sizes. Your alternative hypothesis is ___.
A) 12 < 22
B) 1 - 2 < 0
C) π1 - π2 = 0
D) 1 - 2 = 0
E) s1 - s2 = 0
A) 12 < 22
B) 1 - 2 < 0
C) π1 - π2 = 0
D) 1 - 2 = 0
E) s1 - s2 = 0

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
44
Maureen McIlvoy, owner and CEO of a mail order business for wind surfing equipment and supplies, is reviewing the order filling operations at her warehouses. Her goal is 100% of orders shipped within 24 hours. In previous years, neither warehouse has achieved the goal, but the East Coast Warehouse has consistently out-performed the West Coast Warehouse. Her staff randomly selected 200 orders from the West Coast Warehouse (population 1) and 400 orders from the East Coast Warehouse (population 2), and reports that 190 of the West Coast Orders were shipped within 24 hours, and the East Coast Warehouse shipped 372 orders within 24 hours. Maureen's alternative hypothesis is ___.
A) π1 - π2 0
B) 1 - 2 > 0
C) π1 - π2 > 0
D) 1 - 2 0
E) 1 - 2 ≥ 0
A) π1 - π2 0
B) 1 - 2 > 0
C) π1 - π2 > 0
D) 1 - 2 0
E) 1 - 2 ≥ 0

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
45
Maureen McIlvoy, owner and CEO of a mail order business for wind surfing equipment and supplies, is reviewing the order filling operations at her warehouses. Her goal is 100% of orders shipped within 24 hours. In previous years, neither warehouse has achieved the goal, but the East Coast Warehouse has consistently out-performed the West Coast Warehouse. Her staff randomly selected 200 orders from the West Coast Warehouse (population 1) and 400 orders from the East Coast Warehouse (population 2), and reports that 190 of the West Coast Orders were shipped within 24 hours, and the East Coast Warehouse shipped 356 orders within 24 hours. Assuming = 0.05, the observed z value is ___.
A) -3.15
B) 2.42
C) 1.53
D) 0.95
E) 1.05
A) -3.15
B) 2.42
C) 1.53
D) 0.95
E) 1.05

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
46
A researcher wishes to determine the difference in two population means. To do this, she randomly samples 9 items from each population and computes a 90% confidence interval. The sample from the first population produces a mean of 780 with a standard deviation of 240. The sample from the second population produces a mean of 890 with a standard deviation of 280. Assume that the values are normally distributed in each population. The point estimate for the difference in the means of these two populations is ___.
A) -110
B) 40
C) -40
D) 0
E) 240
A) -110
B) 40
C) -40
D) 0
E) 240

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
47
A researcher believes a new diet should improve weight gain. To test his hypothesis a random sample of 10 people on the old diet and an independent random sample of 10 people on the new diet were selected. The selected people on the old diet gain an average of 5 pounds with a standard deviation of 2 pounds, while the average gain for selected people on the new diet was 8 pounds with a standard deviation of 1.5 pounds. Assume that the values are normally distributed in each population and that the population variances are approximately equal. Using = 0.05, the critical t value used from the table for this is ___.
A) -1.96
B) -1.645
C) -2.100
D) -3.79
E) -1.734
A) -1.96
B) -1.645
C) -2.100
D) -3.79
E) -1.734

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
48
Maureen McIlvoy, owner and CEO of a mail order business for wind surfing equipment and supplies, is reviewing the order filling operations at her warehouses. Her goal is 100% of orders shipped within 24 hours. In previous years, neither warehouse has achieved the goal, but the East Coast Warehouse has consistently out-performed the West Coast Warehouse. Her staff randomly selected 200 orders from the West Coast Warehouse (population 1) and 400 orders from the East Coast Warehouse (population 2), and reports that 190 of the West Coast Orders were shipped within 24 hours, and the East Coast Warehouse shipped 372 orders within 24 hours. Assuming = 0.05, the observed z value is ___.
A) -3.15
B) 2.42
C) 1.53
D) 0.95
E) 1.08
A) -3.15
B) 2.42
C) 1.53
D) 0.95
E) 1.08

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
49
A researcher believes a new diet should improve weight gain. To test his hypothesis a random sample of 10 people on the old diet and an independent random sample of 10 people on the new diet were selected. The selected people on the old diet gain an average of 5 pounds with a standard deviation of 2 pounds, while the average gain for selected people on the new diet was 8 pounds with a standard deviation of 1.5 pounds. Assume that the values are normally distributed in each population and that the population variances are approximately equal. Using = 0.05, the observed t value for this test is ___.
A) -1.96
B) -1.645
C) -2.100
D) -3.79
E) -1.734
A) -1.96
B) -1.645
C) -2.100
D) -3.79
E) -1.734

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
50
You are interested in determining the difference in two population means. You select a random sample of 8 items from the first population and 8 from the second population and then compute a 95% confidence interval. The sample from the first population has an average of 12.2 and a standard deviation of 0.8. The sample from the second population has an average of 11.7 and a standard deviation of 1.0. Assume that the values are normally distributed in each population. The point estimate for the difference in means of these two populations is ___.
A) −0.2
B) 0.2
C) 0.5
D) −0.5
E) 0.06
A) −0.2
B) 0.2
C) 0.5
D) −0.5
E) 0.06

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
51
Maureen McIlvoy, owner and CEO of a mail order business for wind surfing equipment and supplies, is reviewing the order filling operations at her warehouses. Her goal is 100% of orders shipped within 24 hours. In previous years, neither warehouse has achieved the goal, but the East Coast Warehouse has consistently out-performed the West Coast Warehouse. Her staff randomly selected 200 orders from the West Coast Warehouse (population 1) and 400 orders from the East Coast Warehouse (population 2), and reports that 190 of the West Coast Orders were shipped within 24 hours, and the East Coast Warehouse shipped 372 orders within 24 hours. Assuming = 0.05, the appropriate decision is ___.
A) do not reject the null hypothesis 1 - 2 = 0
B) do not reject the null hypothesis π1 - π2 = 0
C) reject the null hypothesis 1 - 2 = 0
D) reject the null hypothesis p1 - p2 = 0
E) do not reject the null hypothesis π1 - π2 ≥ 0
A) do not reject the null hypothesis 1 - 2 = 0
B) do not reject the null hypothesis π1 - π2 = 0
C) reject the null hypothesis 1 - 2 = 0
D) reject the null hypothesis p1 - p2 = 0
E) do not reject the null hypothesis π1 - π2 ≥ 0

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
52
You are interested in determining whether the mean price of electricity offered by solar companies is different in the southern states than in the northern states. You select a random sample of 8 solar companies from the southern states and 11 from the northern states. For the southern states, the average price is 12.2 cents per kWh (kilowatt hour) and the standard deviation is 0.8 cents per kWh. For the northern states, the average and standard deviation are 11.7 and 1.0 cents per kWh respectively. If you use a significance level α = 0.10 and assuming the values are normally distributed in both populations, the critical t value is ___.
A) 1.330
B) 1.729
C) 1.734
D) 1.740
E) 1.747
A) 1.330
B) 1.729
C) 1.734
D) 1.740
E) 1.747

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
53
Your company is evaluating two cloud-based secured data storage services. "Pie in the Sky," the newer service, claims its uploading and downloading speeds are faster than the older service, "Cloudy but Steady Skies." You need to make a decision based on published access times for both services at different times and for varying file sizes. To make your decision, you purchase a statistical study, which indicates that average download time for Pie in the Sky is 0.77 sec. per MB and for Cloudy but Steady Skies is 0.84. Assume that n1 = n2 = 50, 1 = 0.2 and 2 = 0.3. With =.05, the observed z value is ___.
A) -9.71
B) -1.37
C) -0.7
D) 1.37
E) 1.96
A) -9.71
B) -1.37
C) -0.7
D) 1.37
E) 1.96

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
54
Suppose that.06 of each of two populations possess a given characteristic. Samples of size 400 are randomly drawn from each population. The standard deviation for the sampling distribution of differences between the first sample proportion and the second sample proportion (used to calculate the z score) is ___.
A) 0.00300
B) 0.01679
C) 0.05640
D) 0.00014
E) 0.12000
A) 0.00300
B) 0.01679
C) 0.05640
D) 0.00014
E) 0.12000

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
55
A researcher wishes to determine the difference in two population means. To do this, she randomly samples 9 items from each population and computes a 90% confidence interval. The sample from the first population produces a mean of 780 with a standard deviation of 240. The sample from the second population produces a mean of 890 with a standard deviation of 280. Assume that the values are normally distributed in each population and that the population variances are approximately equal. The critical t value used from the table for this is ___.
A) 1.860
B) 1.734
C) 1.746
D) 1.337
E) 2.342
A) 1.860
B) 1.734
C) 1.746
D) 1.337
E) 2.342

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
56
You are interested in determining the difference in two population means. You select a random sample of 8 items from the first population and 8 from the second population and then compute a 95% confidence interval. The sample from the first population has an average of 12.2 and a standard deviation of 0.8. The sample from the second population has an average of 11.7 and a standard deviation of 1.0. Assume that the values are normally distributed in each population and that the population variances are approximately equal. The corresponding critical t value is ___.
A) 1.753
B) 1.761
C) 2.120
D) 2.131
E) 2.145
A) 1.753
B) 1.761
C) 2.120
D) 2.131
E) 2.145

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
57
Your company is evaluating two cloud-based secured data storage services. "Pie in the Sky," the newer service, claims its uploading and downloading speeds are faster than the older service, "Cloudy but Steady Skies." You need to make a decision based on published access times for both services at different times and for varying file sizes. To make your decision, you purchase a statistical study, which indicates that average download time for Pie in the Sky is 0.77 sec. per MB and for Cloudy but Steady Skies is 0.84. Assume that 1 = 0.2 and 2 = 0.3. With =.05, the critical z value is ___.
A) 1.645
B) -1.645
C) 1.96
D) -1.96
E) 2.33
A) 1.645
B) -1.645
C) 1.96
D) -1.96
E) 2.33

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
58
Suppose that.06 of each of two populations possess a given characteristic. Samples of size 400 are randomly drawn from each population. The probability that the difference between the first sample proportion which possess the given characteristic and the second sample proportion which possess the given characteristic being more than +.03 is ___.
A) 0.4943
B) 0.9943
C) 0.0367
D) 0.5057
E) 0.5700
A) 0.4943
B) 0.9943
C) 0.0367
D) 0.5057
E) 0.5700

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
59
Your company is evaluating two cloud-based secured data storage services. "Pie in the Sky," the newer service, claims its uploading and downloading speeds are faster than the older service, "Cloudy but Steady Skies." You need to make a decision based on published access times for both services at different times and for varying file sizes. To make your decision, you purchase a statistical study, which indicates that average download time for Pie in the Sky is 0.77 sec. per MB and for Cloudy but Steady Skies is 0.84. Assume that n1 = n2 = 50, 1 = 0.2 and 2 = 0.3. With =.05, the appropriate decision is ___.
A) reject the null hypothesis 12 < 22
B) accept the alternate hypothesis 1 - 2 > 0
C) reject the alternate hypothesis n1 = n2 = 50
D) fail to reject the null hypothesis 1 - 2 = 0
E) do nothing
A) reject the null hypothesis 12 < 22
B) accept the alternate hypothesis 1 - 2 > 0
C) reject the alternate hypothesis n1 = n2 = 50
D) fail to reject the null hypothesis 1 - 2 = 0
E) do nothing

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
60
Maureen McIlvoy, owner and CEO of a mail order business for wind surfing equipment and supplies, is reviewing the order filling operations at her warehouses. Her goal is 100% of orders shipped within 24 hours. In previous years, neither warehouse has achieved the goal, but the East Coast Warehouse has consistently out-performed the West Coast Warehouse. Her staff randomly selected 200 orders from the West Coast Warehouse (population 1) and 400 orders from the East Coast Warehouse (population 2), and reports that 190 of the West Coast Orders were shipped within 24 hours, and the East Coast Warehouse shipped 372 orders within 24 hours. Maureen's null hypothesis is ___.
A) π1 - π2 = 0
B) 1 - 2 = 0
C) p1 - p2 ≥ 0
D) 1 - 2 ≤ 0
E) 1 - 2 ≥ 0
A) π1 - π2 = 0
B) 1 - 2 = 0
C) p1 - p2 ≥ 0
D) 1 - 2 ≤ 0
E) 1 - 2 ≥ 0

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
61
Maxwell Cantor, VP of human resources of Asimov Aerospace Industries Inc., is reviewing the technical certifications of employees in different divisions of the company. His goal is having 90% of technical employees with up-to-date certifications. The north-east division typically has maintained higher rates of up-to-date certifications than the southern division. He selects a random sample of 250 employees from the north-east division and 300 from the southern division and finds out that the number of employees with up-to-date certifications are 230 in the north-east division and 265 in the southern division. Maxwell's alternative hypothesis is ___.
A) 1 - 2 = 0
B) π1 - π2 ≥ 0
C) 1 - 2 ≤ 0
D) 1 - 2 ≥ 0
E) π1 - π2 = 0
A) 1 - 2 = 0
B) π1 - π2 ≥ 0
C) 1 - 2 ≤ 0
D) 1 - 2 ≥ 0
E) π1 - π2 = 0

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
62
Suppose that the proportion of young adults who read at least one book per month is 0.15, and this proportion is the same in Boston and New York. Suppose that samples of size 400 are randomly drawn from each city. The standard deviation for the sampling distribution of differences between the first sample proportion and the second sample proportion (used to calculate the z score) is ___.
A) 0.0459
B) 0.0435
C) 0.0402
D) 0.0335
E) 0.0319
A) 0.0459
B) 0.0435
C) 0.0402
D) 0.0335
E) 0.0319

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
63
Maxwell Cantor, VP of human resources of Asimov Aerospace Industries Inc., is reviewing the technical certifications of employees in different divisions of the company. His goal is having 90% of technical employees with up-to-date certifications. The north-east division typically has maintained higher rates of up-to-date certifications than the southern division. He selects a random sample of 250 employees from the north-east division and 300 from the southern division and finds out that the number of employees with up-to-date certifications are 230 in the north-east division and 265 in the southern division. Assuming = 0.01, the critical z value is ___.
A) -2.33
B) 1.645
C) 1.96
D) 2.33
E) 2.576
A) -2.33
B) 1.645
C) 1.96
D) 2.33
E) 2.576

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
64
A researcher is interested in estimating the difference in two population proportions. A sample of 400 from each population results in sample proportions of.61 and.64. The point estimate of the difference in the population proportions is ___.
A) -0.030
B) 0.625
C) 0.000
D) 0.400
E) 0.500
A) -0.030
B) 0.625
C) 0.000
D) 0.400
E) 0.500

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
65
A product researcher wants to determine if there is a difference in the rate at which men and women become proficient at using a new software package. A study of 51 men and 46 women produced the following results:
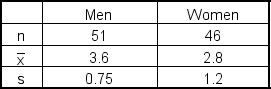 At α = 0.05, is there evidence of a statistically significant difference between the time it takes men to become proficient at this particular software compared to the time it takes women? Assume equal population variances.
At α = 0.05, is there evidence of a statistically significant difference between the time it takes men to become proficient at this particular software compared to the time it takes women? Assume equal population variances.
 At α = 0.05, is there evidence of a statistically significant difference between the time it takes men to become proficient at this particular software compared to the time it takes women? Assume equal population variances.
At α = 0.05, is there evidence of a statistically significant difference between the time it takes men to become proficient at this particular software compared to the time it takes women? Assume equal population variances.
Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
66
Maxwell Cantor, VP of human resources of Asimov Aerospace Industries Inc., is reviewing the technical certifications of employees in different divisions of the company. His goal is having 90% of technical employees with up-to-date certifications. The north-east division typically has maintained higher rates of up-to-date certifications than the southern division. He selects a random sample of 250 employees from the north-east division and 300 from the southern division and finds out that the number of employees with up-to-date certifications are 230 in the north-east division and 265 in the southern division. Assuming = 0.01, the observed z value is ___.
A) 1.027
B) 1.219
C) 1.427
D) 1.619
E) 1.827
A) 1.027
B) 1.219
C) 1.427
D) 1.619
E) 1.827

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
67
Are women more risk averse in the stock market? A sample of men and women were asked the following question: "If both the stock market and a stock you owned dropped 25% in three months, would you buy more shares while price is low?" Of 965 women, 338 said yes. Of 1066 men, 554 said yes.
At the α = 0.05 level of significance, is there evidence that the proportion of women who would buy more shares while the price is low is less than the proportion of men?
At the α = 0.05 level of significance, is there evidence that the proportion of women who would buy more shares while the price is low is less than the proportion of men?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
68
A university administrator believes that business students are more likely to be working and going to school than their liberal arts majors. This information may lead to the business school offering courses in the evening hours while the liberal arts college maintains a daytime schedule. To test this theory the proportion of business students who are working at least 20 hours per week is compared to the proportion of liberal arts students who are working at least 20 hours per week. A random sample of 600 from the business school has been taken and it is determined that 480 students work at least 20 hours per week. A random sample of 700 liberal arts students showed that 350 work at least 20 hours per week. The observed z for this is ___.
A) 0.300
B) 0.624
C) 0.638
D) 11.22
E) 13.42
A) 0.300
B) 0.624
C) 0.638
D) 11.22
E) 13.42

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
69
Suppose that.06 of each of two populations possess a given characteristic. Samples of size 400 are randomly drawn from each population. What is the probability that the differences in sample proportions will be greater than 0.02?
A) 0.4535
B) 0.9535
C) 0.1170
D) 0.5465
E) 0.4650
A) 0.4535
B) 0.9535
C) 0.1170
D) 0.5465
E) 0.4650

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
70
Maxwell Cantor, VP of human resources of Asimov Aerospace Industries Inc., is reviewing the technical certifications of employees in different divisions of the company. His goal is having 90% of technical employees with up-to-date certifications. The north-east division typically has maintained higher rates of up-to-date certifications than the southern division. He selects a random sample of 250 employees from the north-east division and 300 from the southern division and finds out that the number of employees with up-to-date certifications are 230 in the north-east division and 265 in the southern division. Maxwell's null hypothesis is ___.
A) 1 - 2 = 0
B) π1 - π2 ≥ 0
C) 1 - 2 ≤ 0
D) 1 - 2 ≥ 0
E) π1 - π2 = 0
A) 1 - 2 = 0
B) π1 - π2 ≥ 0
C) 1 - 2 ≤ 0
D) 1 - 2 ≥ 0
E) π1 - π2 = 0

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
71
Maxwell Cantor, VP of human resources of Asimov Aerospace Industries Inc., is reviewing the technical certifications of employees in different divisions of the company. His goal is having 90% of technical employees with up-to-date certifications. The north-east division typically has maintained higher rates of up-to-date certifications than the southern division. He selects a random sample of 250 employees from the north-east division and 300 from the southern division and finds out that the number of employees with up-to-date certifications are 230 in the north-east division and 265 in the southern division. Assuming = 0.01, the appropriate decision is ___.
A) do not reject the null hypothesis 1 - 2 = 0
B) do not reject the null hypothesis π1 - π2 = 0
C) reject the null hypothesis 1 - 2 = 0
D) reject the null hypothesis π1 - π2 = 0
E) do not reject the null hypothesis π1 - π2 ≥ 0
A) do not reject the null hypothesis 1 - 2 = 0
B) do not reject the null hypothesis π1 - π2 = 0
C) reject the null hypothesis 1 - 2 = 0
D) reject the null hypothesis π1 - π2 = 0
E) do not reject the null hypothesis π1 - π2 ≥ 0

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck
72
A large corporation wants to determine whether or not the typing efficiency course given at a local college has any influence on typing speed of secretaries. A sample of 6 secretaries is selected, and they are sent to take the course. The typing speed of the secretaries in word per minute (WPM) are shown below:
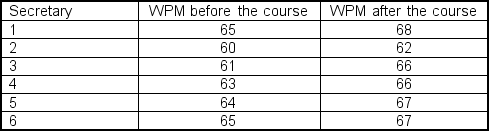 At
At 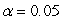
, test if it can be concluded that taking the course increased the typing speed of the secretaries?
 At
At 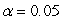
, test if it can be concluded that taking the course increased the typing speed of the secretaries?

Unlock Deck
Unlock for access to all 72 flashcards in this deck.
Unlock Deck
k this deck


