Chat with AI
Deck 27: Factor Models of the Term Structure
Full screen (f)
Question
Question
In the Ho & Lee (1986)model,the parameter 
plays a crucial role.Which of the following statements best describes this parameter?
(a)
)
B)As
Increases the volatility of interest rates increases.
C)As
Increases the volatility of interest rates decreases.
(d)
)
plays a crucial role.Which of the following statements best describes this parameter?(a)
)
B)As
Increases the volatility of interest rates increases.
C)As
Increases the volatility of interest rates decreases.
(d)
)
Question
Question
Assume annual compounding.The one-year and two-year zero-coupon rates in the BDT model are 6% and 7%.The volatility is given to be 
.What is the price of a one-year maturity call option on a 7.5% coupon (annual pay)bond at a strike of $100 (ex-coupon)?
A)0.80
B)0.90
C)1.00
D)1.10
.What is the price of a one-year maturity call option on a 7.5% coupon (annual pay)bond at a strike of $100 (ex-coupon)?A)0.80
B)0.90
C)1.00
D)1.10
Question
In the Ho & Lee (1986)model,assume that the initial curve of zero-coupon discount bond prices for one and two years is 
and 
,respectively.Assume that the probability of an upshift in discount functions is equal to that of a downshift.If the parameter 
,then the price of a one-year zero-coupon bond in the up node after one year will be
A)0.9282
B)0.9496
C)0.9563
D)0.9678
and ,respectively.Assume that the probability of an upshift in discount functions is equal to that of a downshift.If the parameter ,then the price of a one-year zero-coupon bond in the up node after one year will beA)0.9282
B)0.9496
C)0.9563
D)0.9678
Question
Vasicek (1977)posits a general mean-reverting form for the short-rate: 
He then derives,in the absence of arbitrage,a restriction on the market price of risk 
of any bond,where 
of any bond,with 
being the instantaneous return on the bond,and 
being the bond's instantaneous volatility.The derived restriction is that
(a)
Is a constant.
(b)
May be a function of time
,but not of any other time-
Information or of the maturity
Of the bond.
(c)
May be a function of the time-
Short rate
,but not of current time
Or of the bond maturity
)
(d)
May be a function of time
And the time-
Short rate
,but not of the bond maturity
)
He then derives,in the absence of arbitrage,a restriction on the market price of risk of any bond,where of any bond,with being the instantaneous return on the bond,and being the bond's instantaneous volatility.The derived restriction is that(a)
Is a constant.
(b)
May be a function of time
,but not of any other time-
Information or of the maturity
Of the bond.
(c)
May be a function of the time-
Short rate
,but not of current time
Or of the bond maturity
)
(d)
May be a function of time
And the time-
Short rate
,but not of the bond maturity
)
Question
In the Cox-Ingersoll-Ross (1985)model,interest rates are specified by the following stochastic process: 
The process for interest rates is mean-reverting if
(a)
(b)
(c)
(d)
The process for interest rates is mean-reverting if(a)
(b)
(c)
(d)
Question
Assume annual compounding.The one-year and two-year zero-coupon rates in the BDT model are 6% and 7%.The volatility is given to be 
.What is the price of a one-year maturity put option on a 7.5% coupon (annual pay)bond at a strike of $100 (ex-coupon)?
A)1.00
B)1.08
C)1.16
D)1.24
.What is the price of a one-year maturity put option on a 7.5% coupon (annual pay)bond at a strike of $100 (ex-coupon)?A)1.00
B)1.08
C)1.16
D)1.24
Question
In the Cox-Ingersoll-Ross (CIR 1985)model,you are given that 
where 
, 
, 
,and the current short rate of interest is 
.What is the expected short rate of interest one year hence?
A)6.6%
B)7.2%
C)7.6%
D)8.2%
where , , ,and the current short rate of interest is .What is the expected short rate of interest one year hence?A)6.6%
B)7.2%
C)7.6%
D)8.2%
Question
Assume annual compounding.The one-year and two-year zero-coupon rates in the BDT model are 6% and 7%.The volatility is given to be 
.What are the one-year rates (up and down)after one year?
A)9.2% and 6.1%
B)9.6% and 5.8%
C)10.0% and 4.0%
D)10.4% and 5.7%
.What are the one-year rates (up and down)after one year?A)9.2% and 6.1%
B)9.6% and 5.8%
C)10.0% and 4.0%
D)10.4% and 5.7%
Question
In the Cox-Ingersoll-Ross or CIR model,interest rates are specified by the following stochastic process: 
One attractive feature of this process relative to the Vasicek interest rate process 
is that
A)Interest rates are always non-negative in CIR while they may be negative in the Vasicek model.
B)There are parameter restrictions which guarantee non-negative stochastic interest rates in the CIR model,but there are no such restrictions possible in the Vasicek model.
C)It has extra parameters,so can fit observed yield curves better.
D)It allows for imperfect instantaneous correlation between rates of different maturities,whereas in the Vasicek model,they are perfectly correlated.
One attractive feature of this process relative to the Vasicek interest rate process is thatA)Interest rates are always non-negative in CIR while they may be negative in the Vasicek model.
B)There are parameter restrictions which guarantee non-negative stochastic interest rates in the CIR model,but there are no such restrictions possible in the Vasicek model.
C)It has extra parameters,so can fit observed yield curves better.
D)It allows for imperfect instantaneous correlation between rates of different maturities,whereas in the Vasicek model,they are perfectly correlated.
Question
Question
In the Ho & Lee (1986)model,assume that the initial curve of zero-coupon rates for one and two years is 6% and 7%,respectively.Assume that the probability of an upshift in discount functions is equal to that of a downshift.If the parameter 
,then the price of a one-year maturity call option on a two-year $100 face value zero-coupon bond in the up node after one year at a strike of $92 will be
A)1.10
B)1.20
C)1.30
D)1.40
,then the price of a one-year maturity call option on a two-year $100 face value zero-coupon bond in the up node after one year at a strike of $92 will beA)1.10
B)1.20
C)1.30
D)1.40
Question
In the CIR (1985)model,which of the following statements is true? The price of the bond increases when
A)The short rate
Increases.
B)The rate of mean reversion
Rises.
C)The long-run mean rate
Increases.
D)The volatility
Increases.
A)The short rate
Increases.
B)The rate of mean reversion
Rises.
C)The long-run mean rate
Increases.
D)The volatility
Increases.
Question
Assume annual compounding.The one-year and two-year zero-coupon rates in the BDT model are 6% and 7%.The volatility is given to be 
.At what strike price will one-year maturity call and put options on a 7.5% coupon (annual pay)bond at a strike of $100 (ex-coupon)have equal prices?
A)$98.32
B)$99.52
C)$100.12
D)$101.42
.At what strike price will one-year maturity call and put options on a 7.5% coupon (annual pay)bond at a strike of $100 (ex-coupon)have equal prices?A)$98.32
B)$99.52
C)$100.12
D)$101.42
Question
Question
In the Vasieck (1977)model,you are given that 
where 
, 
, 
,and the current short rate of interest is 
.What is the expected standard deviation of the short rate of interest one year hence?
A)0.08
B)0.09
C)0.10
D)0.11
where , , ,and the current short rate of interest is .What is the expected standard deviation of the short rate of interest one year hence?A)0.08
B)0.09
C)0.10
D)0.11
Question
Assume annual compounding.The one-year and two-year zero-coupon rates in the BDT model are 6% and 7%.The volatility is given to be 
.What is the price of a one-year maturity cap on the one-year interest rate at a strike rate of 8% and a notional of $100?
A)1.000
B)1.025
C)1.050
D)1.075
.What is the price of a one-year maturity cap on the one-year interest rate at a strike rate of 8% and a notional of $100?A)1.000
B)1.025
C)1.050
D)1.075
Question
Assume annual compounding.The one-year and two-year zero-coupon rates in the BDT model are 6% and 7%.The volatility is given to be 
.What is the price of a one-year maturity floor on the one-year interest rate at a strike rate of 8% and a notional of $100?
A)1.000
B)1.026
C)1.052
D)1.078
.What is the price of a one-year maturity floor on the one-year interest rate at a strike rate of 8% and a notional of $100?A)1.000
B)1.026
C)1.052
D)1.078
Question
A one-factor bond pricing model implies that interest-rates of all maturities are driven by a single source of stochastic randomness.For example the system of interest rates may be described by the following equation: 
where 
denotes the maturity of different rates.A single-factor model implies that
A)All rates either move up together or all move down together.
B)The yield curve experience parallel shifts.
C)Instantaneous changes in rates of all maturities are perfectly positively or negatively correlated with each other.
D)Twists in shape of the yield curve are not possible.
where denotes the maturity of different rates.A single-factor model implies thatA)All rates either move up together or all move down together.
B)The yield curve experience parallel shifts.
C)Instantaneous changes in rates of all maturities are perfectly positively or negatively correlated with each other.
D)Twists in shape of the yield curve are not possible.
Question
In the Cox-Ingersoll-Ross (CIR 1985)model,you are given that 
where 
, 
, 
.If the yield of a five-year bond is 
,then what is the price of the bond?
A)0.65
B)0.70
C)0.75
D)0.80
where , , .If the yield of a five-year bond is ,then what is the price of the bond?A)0.65
B)0.70
C)0.75
D)0.80
Question
An affine factor model is one in which multiple factors 
may be present.Which of the following is not true of an affine factor model.
A)The drift
Will be linear in
)
B)The volatility
Will be linear in
)
C)The yield
Will be linear in
)
D)The logarithm of the price scaled by maturity is the yield.
may be present.Which of the following is not true of an affine factor model.A)The drift
Will be linear in
)
B)The volatility
Will be linear in
)
C)The yield
Will be linear in
)
D)The logarithm of the price scaled by maturity is the yield.
Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/22
Play
Full screen (f)
Deck 27: Factor Models of the Term Structure
1
An exponential-affine short rate bond model is one
A)That most bond traders have an affinity for.
B)Where the bond prices are linear in the short-rate.
C)Where the logarithm of bond prices is linear in the short rate.
D)Where the bond price is based on discrete compounding.
A)That most bond traders have an affinity for.
B)Where the bond prices are linear in the short-rate.
C)Where the logarithm of bond prices is linear in the short rate.
D)Where the bond price is based on discrete compounding.
C
Exponential-affine bond models have prices that take the following functional form: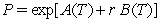
,where 
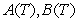are functions of time but not of the short rate.Therefore,the natural logarithm of the price is linear in the short rate 
.
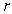Exponential-affine bond models have prices that take the following functional form:
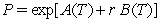,where 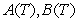are functions of time but not of the short rate.Therefore,the natural logarithm of the price is linear in the short rate 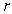. 2
In the Ho & Lee (1986)model,the parameter 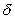plays a crucial role.Which of the following statements best describes this parameter?
(a)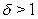
)
B)As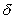
Increases the volatility of interest rates increases.
C)As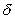
Increases the volatility of interest rates decreases.
(d)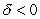
)
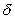plays a crucial role.Which of the following statements best describes this parameter?(a)
)
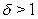
B)As
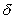
Increases the volatility of interest rates increases.
C)As
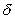
Increases the volatility of interest rates decreases.
(d)
)
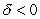
C
We have that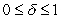
.This can be seen from the fact that the upshift and downshift functions that multiple the forward discount function are 
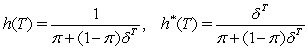respectively,where 
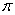is the probability of the upshift.As 
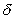decreases,the divergence between 
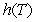and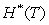 
increases.
We have that
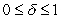.This can be seen from the fact that the upshift and downshift functions that multiple the forward discount function are 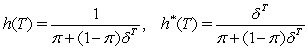respectively,where 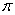is the probability of the upshift.As 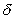decreases,the divergence between 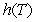and 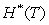increases. 3
In the Black-Derman-Toy (BDT)model,short rates are distributed as
A)Normal
B)Lognormal
C)Exponential
D)None of the above
A)Normal
B)Lognormal
C)Exponential
D)None of the above
B
4
Assume annual compounding.The one-year and two-year zero-coupon rates in the BDT model are 6% and 7%.The volatility is given to be 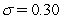.What is the price of a one-year maturity call option on a 7.5% coupon (annual pay)bond at a strike of $100 (ex-coupon)?
A)0.80
B)0.90
C)1.00
D)1.10
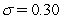.What is the price of a one-year maturity call option on a 7.5% coupon (annual pay)bond at a strike of $100 (ex-coupon)?A)0.80
B)0.90
C)1.00
D)1.10
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
5
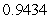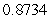In the Ho & Lee (1986)model,assume that the initial curve of zero-coupon discount bond prices for one and two years is and ,respectively.Assume that the probability of an upshift in discount functions is equal to that of a downshift.If the parameter 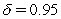,then the price of a one-year zero-coupon bond in the up node after one year will be
A)0.9282
B)0.9496
C)0.9563
D)0.9678
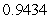and 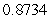,respectively.Assume that the probability of an upshift in discount functions is equal to that of a downshift.If the parameter 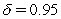,then the price of a one-year zero-coupon bond in the up node after one year will beA)0.9282
B)0.9496
C)0.9563
D)0.9678
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
6
Vasicek (1977)posits a general mean-reverting form for the short-rate: 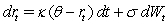He then derives,in the absence of arbitrage,a restriction on the market price of risk 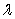of any bond,where 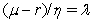of any bond,with 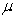being the instantaneous return on the bond,and 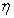being the bond's instantaneous volatility.The derived restriction is that
(a)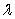
Is a constant.
(b)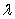
May be a function of time
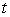
,but not of any other time-
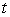
Information or of the maturity
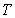
Of the bond.
(c)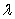
May be a function of the time-
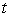
Short rate
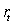
,but not of current time
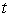
Or of the bond maturity
)
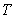
(d)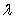
May be a function of time
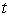
And the time-
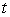
Short rate
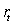
,but not of the bond maturity
)
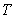
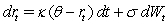He then derives,in the absence of arbitrage,a restriction on the market price of risk 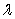of any bond,where 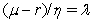of any bond,with 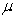being the instantaneous return on the bond,and 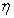being the bond's instantaneous volatility.The derived restriction is that(a)
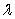
Is a constant.
(b)
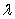
May be a function of time
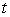
,but not of any other time-
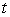
Information or of the maturity
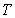
Of the bond.
(c)
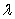
May be a function of the time-
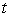
Short rate
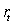
,but not of current time
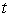
Or of the bond maturity
)
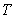
(d)
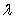
May be a function of time
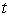
And the time-
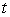
Short rate
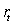
,but not of the bond maturity
)
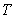
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
7
In the Cox-Ingersoll-Ross (1985)model,interest rates are specified by the following stochastic process: 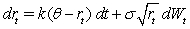The process for interest rates is mean-reverting if
(a)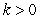
(b)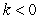
(c)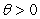
(d)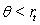
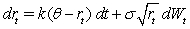The process for interest rates is mean-reverting if(a)
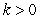
(b)
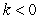
(c)
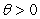
(d)
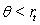
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
8
Assume annual compounding.The one-year and two-year zero-coupon rates in the BDT model are 6% and 7%.The volatility is given to be 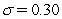.What is the price of a one-year maturity put option on a 7.5% coupon (annual pay)bond at a strike of $100 (ex-coupon)?
A)1.00
B)1.08
C)1.16
D)1.24
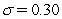.What is the price of a one-year maturity put option on a 7.5% coupon (annual pay)bond at a strike of $100 (ex-coupon)?A)1.00
B)1.08
C)1.16
D)1.24
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
9
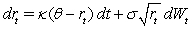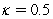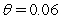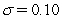In the Cox-Ingersoll-Ross (CIR 1985)model,you are given that where , , ,and the current short rate of interest is 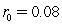.What is the expected short rate of interest one year hence?
A)6.6%
B)7.2%
C)7.6%
D)8.2%
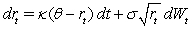where 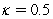, , 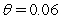,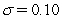and the current short rate of interest is 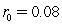.What is the expected short rate of interest one year hence?A)6.6%
B)7.2%
C)7.6%
D)8.2%
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
10
Assume annual compounding.The one-year and two-year zero-coupon rates in the BDT model are 6% and 7%.The volatility is given to be 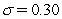.What are the one-year rates (up and down)after one year?
A)9.2% and 6.1%
B)9.6% and 5.8%
C)10.0% and 4.0%
D)10.4% and 5.7%
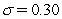.What are the one-year rates (up and down)after one year?A)9.2% and 6.1%
B)9.6% and 5.8%
C)10.0% and 4.0%
D)10.4% and 5.7%
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
11
In the Cox-Ingersoll-Ross or CIR model,interest rates are specified by the following stochastic process: 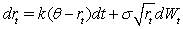One attractive feature of this process relative to the Vasicek interest rate process 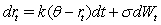is that
A)Interest rates are always non-negative in CIR while they may be negative in the Vasicek model.
B)There are parameter restrictions which guarantee non-negative stochastic interest rates in the CIR model,but there are no such restrictions possible in the Vasicek model.
C)It has extra parameters,so can fit observed yield curves better.
D)It allows for imperfect instantaneous correlation between rates of different maturities,whereas in the Vasicek model,they are perfectly correlated.
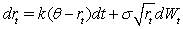One attractive feature of this process relative to the Vasicek interest rate process 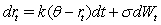is thatA)Interest rates are always non-negative in CIR while they may be negative in the Vasicek model.
B)There are parameter restrictions which guarantee non-negative stochastic interest rates in the CIR model,but there are no such restrictions possible in the Vasicek model.
C)It has extra parameters,so can fit observed yield curves better.
D)It allows for imperfect instantaneous correlation between rates of different maturities,whereas in the Vasicek model,they are perfectly correlated.
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
12
The Ho & Lee (1986)model directly models the following on a binomial tree:
A)Yields.
B)Discount functions.
C)Zero-coupon rates.
D)Forward rates.
A)Yields.
B)Discount functions.
C)Zero-coupon rates.
D)Forward rates.
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
13
In the Ho & Lee (1986)model,assume that the initial curve of zero-coupon rates for one and two years is 6% and 7%,respectively.Assume that the probability of an upshift in discount functions is equal to that of a downshift.If the parameter 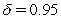,then the price of a one-year maturity call option on a two-year $100 face value zero-coupon bond in the up node after one year at a strike of $92 will be
A)1.10
B)1.20
C)1.30
D)1.40
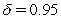,then the price of a one-year maturity call option on a two-year $100 face value zero-coupon bond in the up node after one year at a strike of $92 will beA)1.10
B)1.20
C)1.30
D)1.40
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
14
In the CIR (1985)model,which of the following statements is true? The price of the bond increases when
A)The short rate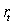
Increases.
B)The rate of mean reversion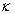
Rises.
C)The long-run mean rate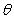
Increases.
D)The volatility
Increases.
A)The short rate
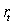
Increases.
B)The rate of mean reversion
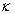
Rises.
C)The long-run mean rate
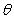
Increases.
D)The volatility
Increases.
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
15
Assume annual compounding.The one-year and two-year zero-coupon rates in the BDT model are 6% and 7%.The volatility is given to be 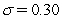.At what strike price will one-year maturity call and put options on a 7.5% coupon (annual pay)bond at a strike of $100 (ex-coupon)have equal prices?
A)$98.32
B)$99.52
C)$100.12
D)$101.42
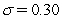.At what strike price will one-year maturity call and put options on a 7.5% coupon (annual pay)bond at a strike of $100 (ex-coupon)have equal prices?A)$98.32
B)$99.52
C)$100.12
D)$101.42
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
16
In the Black-Derman-Toy (BDT)model,short rates have
A)Constant volatility for all maturities.
B)Volatility that changes by maturity of the short rate.
C)Volatility that varies by maturity and level of the short rate,i.e. ,state-dependent volatility.
D)Stochastic volatility.
A)Constant volatility for all maturities.
B)Volatility that changes by maturity of the short rate.
C)Volatility that varies by maturity and level of the short rate,i.e. ,state-dependent volatility.
D)Stochastic volatility.
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
17
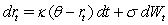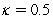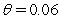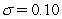In the Vasieck (1977)model,you are given that where , , ,and the current short rate of interest is 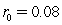.What is the expected standard deviation of the short rate of interest one year hence?
A)0.08
B)0.09
C)0.10
D)0.11
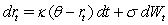where 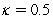, , 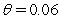,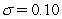and the current short rate of interest is 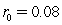.What is the expected standard deviation of the short rate of interest one year hence?A)0.08
B)0.09
C)0.10
D)0.11
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
18
Assume annual compounding.The one-year and two-year zero-coupon rates in the BDT model are 6% and 7%.The volatility is given to be 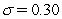.What is the price of a one-year maturity cap on the one-year interest rate at a strike rate of 8% and a notional of $100?
A)1.000
B)1.025
C)1.050
D)1.075
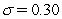.What is the price of a one-year maturity cap on the one-year interest rate at a strike rate of 8% and a notional of $100?A)1.000
B)1.025
C)1.050
D)1.075
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
19
Assume annual compounding.The one-year and two-year zero-coupon rates in the BDT model are 6% and 7%.The volatility is given to be 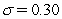.What is the price of a one-year maturity floor on the one-year interest rate at a strike rate of 8% and a notional of $100?
A)1.000
B)1.026
C)1.052
D)1.078
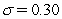.What is the price of a one-year maturity floor on the one-year interest rate at a strike rate of 8% and a notional of $100?A)1.000
B)1.026
C)1.052
D)1.078
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
20
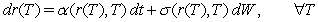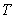A one-factor bond pricing model implies that interest-rates of all maturities are driven by a single source of stochastic randomness.For example the system of interest rates may be described by the following equation: where denotes the maturity of different rates.A single-factor model implies that
A)All rates either move up together or all move down together.
B)The yield curve experience parallel shifts.
C)Instantaneous changes in rates of all maturities are perfectly positively or negatively correlated with each other.
D)Twists in shape of the yield curve are not possible.
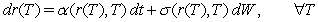where 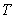denotes the maturity of different rates.A single-factor model implies thatA)All rates either move up together or all move down together.
B)The yield curve experience parallel shifts.
C)Instantaneous changes in rates of all maturities are perfectly positively or negatively correlated with each other.
D)Twists in shape of the yield curve are not possible.
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
21
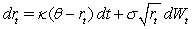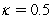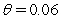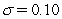In the Cox-Ingersoll-Ross (CIR 1985)model,you are given that where , , .If the yield of a five-year bond is 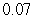,then what is the price of the bond?
A)0.65
B)0.70
C)0.75
D)0.80
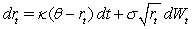where 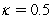, , 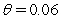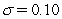.If the yield of a five-year bond is 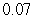,then what is the price of the bond?A)0.65
B)0.70
C)0.75
D)0.80
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
22
An affine factor model is one in which multiple factors 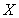may be present.Which of the following is not true of an affine factor model.
A)The drift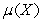
Will be linear in
)
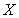
B)The volatility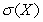
Will be linear in
)
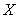
C)The yield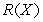
Will be linear in
)
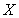
D)The logarithm of the price scaled by maturity is the yield.
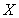may be present.Which of the following is not true of an affine factor model.A)The drift
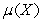
Will be linear in
)
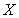
B)The volatility
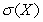
Will be linear in
)
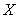
C)The yield
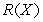
Will be linear in
)
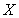
D)The logarithm of the price scaled by maturity is the yield.
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
Unlock Deck
k this deck
Unlock Deck
Unlock for access to all 22 flashcards in this deck.
