Deck 35: A: Public Goods
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/20
Play
Full screen (f)
Deck 35: A: Public Goods
1
Recall Bob and Ray in Problem 4. They are thinking of buying a sofa. Bob's utility function is UB(S, MB) = (1 + S)MB and Ray's utility function is UR(S, MR) = (3 + S)MR, where S = 0 if they don't get the sofa and S = 1 if they do and where MB and MR are the amounts of money they have respectively to spend on their private consumptions. Bob has a total of $2,000 to spend on the sofa and other stuff. Ray has a total of $1,600 to spend on the sofa and other stuff. The maximum amount that they could pay for the sofa and still arrange to both be better off than without it is
A) $2,100.
B) $533.33.
C) $750.
D) $1,400.
E) $2,800.
A) $2,100.
B) $533.33.
C) $750.
D) $1,400.
E) $2,800.
D
2
Recall Bonnie and Clyde from Problem 5. Suppose that their total profits are 140H, where H is the number of hours they work per year. Their utility functions are, respectively, UB(CB, H) = CB - 0.03H2 and UC(CC, H) = CC - 0.02H2, where CB and CC are their private goods consumptions and H is the number of hours they work per year. If they find a Pareto optimal choice of hours of work and income distribution, the number of hours they work per year is a. 1,400.
B) 2,100.
C) 1,500.
D) 650.
E) 750.
B) 2,100.
C) 1,500.
D) 650.
E) 750.
A
3
Recall Bonnie and Clyde from Problem 5. Suppose that their total profits are 72H, where H is the number of hours they work per year. Their utility functions are, respectively, UB(CB, H) = CB - 0.03H2 and UC(CC, H) = CC - 0.03H2, where CB and CC are their private goods consumptions and H is the number of hours they work per year. If they find a Pareto optimal choice of hours of work and income distribution, the number of hours they work per year is a. 600.
B) 700.
C) 900.
D) 250.
E) 350.
B) 700.
C) 900.
D) 250.
E) 350.
A
4
Recall Lucy and Melvin from Problem 6. Lucy's utility function is 2XL + G and Melvin's utility function is XMG, where G is their expenditures on the public goods they share in their apartment and where XL and XM are their respective private consumption expenditures. The total amount they have to spend on private goods and public goods is $24,000. They agree on a Pareto optimal pattern of expenditures in which the amount that is spent on Lucy's private consumption is $6,000. How much do they spend on public goods?
A) $6,000
B) $3,000
C) $6,050
D) $12,000
E) There is not enough information here to be able to determine the answer.
A) $6,000
B) $3,000
C) $6,050
D) $12,000
E) There is not enough information here to be able to determine the answer.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
5
Recall Bonnie and Clyde from Problem 5. Suppose that their total profits are 256H, where H is the number of hours they work per year. Their utility functions are, respectively, UB(CB, H) = CB - 0.04H2 and UC(CC, H) = CC - 0.04H2, where CB and CC are their private goods consumptions and H is the number of hours they work per year. If they find a Pareto optimal choice of hours of work and income distribution, the number of hours they work per year is a. 2,400.
B) 1,600.
C) 1,700.
D) 750.
E) 850.
B) 1,600.
C) 1,700.
D) 750.
E) 850.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
6
Recall Bob and Ray in Problem 4. They are thinking of buying a sofa. Bob's utility function is UB(S, MB) = (1 + S)MB and Ray's utility function is UR(S, MR) = (2 + S)MR, where S = 0 if they don't get the sofa and S = 1 if they do and where MB and MR are the amounts of money they have respectively to spend on their private consumptions. Bob has a total of $1,200 to spend on the sofa and other stuff. Ray has a total of $1,200 to spend on the sofa and other stuff. The maximum amount that they could pay for the sofa and still arrange to both be better off than without it is
A) $1,500.
B) $600.
C) $1,000.
D) $550.
E) $2,000.
A) $1,500.
B) $600.
C) $1,000.
D) $550.
E) $2,000.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
7
Recall Bonnie and Clyde from Problem 5. Suppose that their total profits are 192H, where H is the number of hours they work per year. Their utility functions are, respectively, UB(CB, H) = CB - 0.02H2 and UC(CC, H) = CC - 0.04H2, where CB and CC are their private goods consumptions and H is the number of hours they work per year. If they find a Pareto optimal choice of hours of work and income distribution, the number of hours they work per year is a. 750.
B) 2,400.
C) 1,700.
D) 1,600.
E) 850.
B) 2,400.
C) 1,700.
D) 1,600.
E) 850.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
8
Just north of the town of Muskrat, Ontario, in Problem 1, is the town of Brass Monkey, population 800. Brass Monkey, like Muskrat, has a single public good, the town skating rink and a single private good, Labatt Ale. Everyone's utility function is Ui(Xi, Y) = Xi - 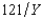 , where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $8 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?
, where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $8 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?
A) 230 square meters.
B) 110 square meters.
C) 225 square meters.
D) 115 square meters.
E) None of the above.
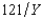 , where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $8 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?
, where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $8 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?A) 230 square meters.
B) 110 square meters.
C) 225 square meters.
D) 115 square meters.
E) None of the above.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
9
Recall Bob and Ray in Problem 4. They are thinking of buying a sofa. Bob's utility function is UB(S, MB) = (1 + S)MB and Ray's utility function is UR(S, MR) = (4 + S)MR, where S = 0 if they don't get the sofa and S = 1 if they do and where MB and MR are the amounts of money they have respectively to spend on their private consumptions. Bob has a total of $800 to spend on the sofa and other stuff. Ray has a total of $4,000 to spend on the sofa and other stuff. The maximum amount that they could pay for the sofa and still arrange to both be better off than without it is
A) $1,000.
B) $1,200.
C) $1,800.
D) $650.
E) $2,400.
A) $1,000.
B) $1,200.
C) $1,800.
D) $650.
E) $2,400.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
10
Recall Bonnie and Clyde from Problem 5. Suppose that their total profits are 160H, where H is the number of hours they work per year. Their utility functions are, respectively, UB(CB, H) = CB - 0.01H2 and UC(CC, H) = CC - 0.04H2, where CB and CC are their private goods consumptions and H is the number of hours they work per year. If they find a Pareto optimal choice of hours of work and income distribution, the number of hours they work per year is a. 1,700.
B) 2,400.
C) 1,600.
D) 750.
E) 850.
B) 2,400.
C) 1,600.
D) 750.
E) 850.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
11
Recall Lucy and Melvin from Problem 6. Lucy's utility function is 2XL + G and Melvin's utility function is XMG, where G is their expenditures on the public goods they share in their apartment and where XL and XM are their respective private consumption expenditures. The total amount they have to spend on private goods and public goods is $39,000. They agree on a Pareto optimal pattern of expenditures in which the amount that is spent on Lucy's private consumption is $9,000. How much do they spend on public goods?
A) $9,550
B) $20,000
C) $5,000
D) $10,000
E) There is not enough information here to be able to determine the answer.
A) $9,550
B) $20,000
C) $5,000
D) $10,000
E) There is not enough information here to be able to determine the answer.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
12
Recall Bob and Ray in Problem 4. They are thinking of buying a sofa. Bob's utility function is UB(S, MB) = (1 + S)MB and Ray's utility function is UR(S, MR) = (2 + S)MR, where S = 0 if they don't get the sofa and S = 1 if they do and where MB and MR are the amounts of money they have respectively to spend on their private consumptions. Bob has a total of $2,000 to spend on the sofa and other stuff. Ray has a total of $3,000 to spend on the sofa and other stuff. The maximum amount that they could pay for the sofa and still arrange to both be better off than without it is
A) $3,000.
B) $1,500.
C) $2,000.
D) $1,050.
E) $4,000.
A) $3,000.
B) $1,500.
C) $2,000.
D) $1,050.
E) $4,000.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
13
Recall Lucy and Melvin from Problem 6. Lucy's utility function is 2XL + G and Melvin's utility function is XMG, where G is their expenditures on the public goods they share in their apartment and where XL and XM are their respective private consumption expenditures. The total amount they have to spend on private goods and public goods is $33,000. They agree on a Pareto optimal pattern of expenditures in which the amount that is spent on Lucy's private consumption is $9,000. How much do they spend on public goods?
A) $8,550
B) $4,000
C) $8,000
D) $16,000
E) There is not enough information here to be able to determine the answer.
A) $8,550
B) $4,000
C) $8,000
D) $16,000
E) There is not enough information here to be able to determine the answer.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
14
Recall Lucy and Melvin from Problem 6. Lucy's utility function is 2XL + G and Melvin's utility function is XMG, where G is their expenditures on the public goods they share in their apartment and where XL and XM are their respective private consumption expenditures. The total amount they have to spend on private goods and public goods is $24,000. They agree on a Pareto optimal pattern of expenditures in which the amount that is spent on Lucy's private consumption is $9,000. How much do they spend on public goods?
A) $5,000
B) $10,000
C) $7,050
D) $2,500
E) There is not enough information here to be able to determine the answer.
A) $5,000
B) $10,000
C) $7,050
D) $2,500
E) There is not enough information here to be able to determine the answer.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
15
Recall Lucy and Melvin from Problem 6. Lucy's utility function is 2XL + G and Melvin's utility function is XMG, where G is their expenditures on the public goods they share in their apartment and where XL and XM are their respective private consumption expenditures. The total amount they have to spend on private goods and public goods is $21,000. They agree on a Pareto optimal pattern of expenditures in which the amount that is spent on Lucy's private consumption is $6,000. How much do they spend on public goods?
A) $5,550
B) $10,000
C) $2,500
D) $5,000
E) There is not enough information here to be able to determine the answer.
A) $5,550
B) $10,000
C) $2,500
D) $5,000
E) There is not enough information here to be able to determine the answer.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
16
Just north of the town of Muskrat, Ontario, in Problem 1, is the town of Brass Monkey, population 4,500. Brass Monkey, like Muskrat, has a single public good, the town skating rink and a single private good, Labatt Ale. Everyone's utility function is Ui(Xi, Y) = Xi - 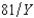 , where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $5 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?
, where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $5 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?
A) 270 square meters.
B) 390 square meters.
C) 195 square meters.
D) 545 square meters.
E) None of the above.
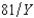 , where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $5 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?
, where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $5 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?A) 270 square meters.
B) 390 square meters.
C) 195 square meters.
D) 545 square meters.
E) None of the above.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
17
Just north of the town of Muskrat, Ontario, in Problem 1, is the town of Brass Monkey, population 700. Brass Monkey, like Muskrat, has a single public good, the town skating rink and a single private good, Labatt Ale. Everyone's utility function is Ui(Xi, Y) = Xi - 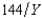 , where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $7 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?
, where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $7 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?
A) 120 square meters.
B) 245 square meters.
C) 240 square meters.
D) 120 square meters.
E) None of the above.
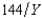 , where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $7 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?
, where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $7 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?A) 120 square meters.
B) 245 square meters.
C) 240 square meters.
D) 120 square meters.
E) None of the above.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
18
Just north of the town of Muskrat, Ontario, in Problem 1, is the town of Brass Monkey, population 700. Brass Monkey, like Muskrat, has a single public good, the town skating rink and a single private good, Labatt Ale. Everyone's utility function is Ui(Xi, Y) = Xi - 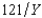 , where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $7 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?
, where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $7 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?
A) 110 square meters.
B) 115 square meters.
C) 230 square meters.
D) 225 square meters.
E) None of the above.
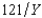 , where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $7 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?
, where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $7 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?A) 110 square meters.
B) 115 square meters.
C) 230 square meters.
D) 225 square meters.
E) None of the above.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
19
Just north of the town of Muskrat, Ontario, in Problem 1, is the town of Brass Monkey, population 12,800. Brass Monkey, like Muskrat, has a single public good, the town skating rink and a single private good, Labatt Ale. Everyone's utility function is Ui(Xi, Y) = Xi - 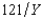 , where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $8 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?
, where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $8 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?
A) 560 square meters.
B) 885 square meters.
C) 280 square meters.
D) 440 square meters.
E) None of the above.
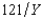 , where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $8 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?
, where Xi is the number of bottles of ale consumed by i and Y is the size of the skating rink in square meters. The price of ale is $1 per bottle. The cost of the skating rink to the city is $8 per square meter. Everyone has an income of at least $5,000. What is the Pareto efficient size for the town skating rink?A) 560 square meters.
B) 885 square meters.
C) 280 square meters.
D) 440 square meters.
E) None of the above.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
20
Recall Bob and Ray in Problem 4. They are thinking of buying a sofa. Bob's utility function is UB(S, MB) = (1 + S)MB and Ray's utility function is UR(S, MR) = (3 + S)MR, where S = 0 if they don't get the sofa and S = 1 if they do and where MB and MR are the amounts of money they have respectively to spend on their private consumptions. Bob has a total of $1,200 to spend on the sofa and other stuff. Ray has a total of $4,000 to spend on the sofa and other stuff. The maximum amount that they could pay for the sofa and still arrange to both be better off than without it is
A) $1,333.33.
B) $1,600.
C) $850.
D) $2,400.
E) $3,200.
A) $1,333.33.
B) $1,600.
C) $850.
D) $2,400.
E) $3,200.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck


