Deck 12: Analysis of Variance
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/128
Play
Full screen (f)
Deck 12: Analysis of Variance
1
Which statement is correct about the F distribution?
A) Cannot be negative
B) Cannot be positive
C) Is the same as the t distribution
D) Is the same as the z distribution
A) Cannot be negative
B) Cannot be positive
C) Is the same as the t distribution
D) Is the same as the z distribution
A
2
For the hypothesis test, 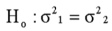 , with n1 = 10 and n2 = 10, the F-test statistic is 2.56. At the 0.01 level of significance, we would reject the null hypothesis.
, with n1 = 10 and n2 = 10, the F-test statistic is 2.56. At the 0.01 level of significance, we would reject the null hypothesis.
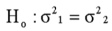 , with n1 = 10 and n2 = 10, the F-test statistic is 2.56. At the 0.01 level of significance, we would reject the null hypothesis.
, with n1 = 10 and n2 = 10, the F-test statistic is 2.56. At the 0.01 level of significance, we would reject the null hypothesis.False
3
Interaction between two factors occurs when the effect of one factor on the response variable is the same for any value of another factor.
False
4
One characteristic of the F distribution is that the computed F can only range between -1 and +1.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
5
In an ANOVA table, k represents the total number of sample observations and n represents the total number of treatments.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
6
Analysis of variance is used to
A) compare nominal data.
B) compute t test.
C) compare population proportions.
D) simultaneously compare several population means.
A) compare nominal data.
B) compute t test.
C) compare population proportions.
D) simultaneously compare several population means.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
7
When a blocking effect is included in an ANOVA, the analysis is more likely to detect differences in the treatment means.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
8
For an ANOVA test, rejection of the null hypothesis does not identify which treatment means differ significantly.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
9
To employ ANOVA, the populations should have approximately equal standard deviations.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
10
The alternative hypothesis used in ANOVA is 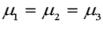 .
.
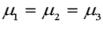 .
.
Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
11
An F statistic is:
A) a ratio of two means.
B) a ratio of two variances.
C) the difference between three means.
D) a population parameter.
A) a ratio of two means.
B) a ratio of two variances.
C) the difference between three means.
D) a population parameter.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
12
In a two-way ANOVA with interaction, there are two factor effects and an interaction effect.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
13
When a blocking effect is included in an ANOVA, the result is a larger error sum of squares.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
14
To employ ANOVA, the populations being studied must be approximately normally distributed.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
15
If the computed value of F is 0.99 and the critical value is 3.89, we would not reject the null hypothesis.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
16
The F distribution's curve is positively skewed.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
17
If a confidence interval for the difference between a pair of treatment means includes 0, then we reject the null hypothesis that there is no difference in the pair of treatment means.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
18
What distribution does the F distribution approach as the sample size increases?
A) Binomial
B) Normal
C) Poisson
D) Exponential
A) Binomial
B) Normal
C) Poisson
D) Exponential

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
19
If we want to determine which treatment means differ, we compute a confidence interval for the difference between each pair of means.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
20
A large department store examined a sample of the 18 credit card sales and recorded the amounts charged for each of three types of credit cards: MasterCard, Visa and Discover. Six MasterCard sales, seven Visa and five Discover sales were recorded. The store used an ANOVA to test if the mean sales for each credit card were equal. What are the degrees of freedom for the F statistic?
A) 18 in the numerator, 3 in the denominator
B) 3 in the numerator, 18 in the denominator
C) 2 in the numerator, 15 in the denominator
D) 6 in the numerator, 15 in the denominator
A) 18 in the numerator, 3 in the denominator
B) 3 in the numerator, 18 in the denominator
C) 2 in the numerator, 15 in the denominator
D) 6 in the numerator, 15 in the denominator

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
21
When testing for differences between treatment means, the t statistic is based on:
A) The treatment degrees of freedom.
B) The total degrees of freedom.
C) The error degrees of freedom.
D) The ratio of treatment and error degrees of freedom.
A) The treatment degrees of freedom.
B) The total degrees of freedom.
C) The error degrees of freedom.
D) The ratio of treatment and error degrees of freedom.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
22
Suppose that an automobile manufacturer designed a radically new lightweight engine and wants to recommend the grade of gasoline that will have the best fuel economy. The four grades are: regular, below regular, premium, and super premium. The test car made three trial runs on the test track using each of the four grades and the miles per gallon recorded. At the 0.05 level, what is the critical value of F used to test the hypothesis that the miles per gallon for each fuel is the same? 
A) 1.96
B) 4.07
C) 2.33
D) 12.00

A) 1.96
B) 4.07
C) 2.33
D) 12.00

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
23
A manufacturer of automobile transmissions uses three different processes. Management ordered a study of the production costs to see if there is a difference among the three processes. A summary of the findings is shown below.  What are the degrees of freedom for the treatment sum of squares?
What are the degrees of freedom for the treatment sum of squares?
A) 2
B) 3
C) 10
D) 27
 What are the degrees of freedom for the treatment sum of squares?
What are the degrees of freedom for the treatment sum of squares?A) 2
B) 3
C) 10
D) 27

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
24
If an ANOVA test is conducted and the null hypothesis is rejected, what does this indicate?
A) Too many degrees of freedom
B) No difference between the population means
C) A difference between at least one pair of population means
D) All population means are different
A) Too many degrees of freedom
B) No difference between the population means
C) A difference between at least one pair of population means
D) All population means are different

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
25
A manufacturer of automobile transmissions uses two different processes. Management ordered a study of the production costs to see if there is a difference among the two processes. A summary of the findings is shown below. 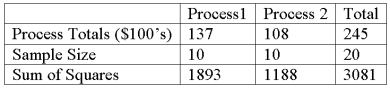 What is the critical value of F at the 5% level of significance?
What is the critical value of F at the 5% level of significance?
A) 19.45
B) 3.00
C) 4.41
D) 4.38
 What is the critical value of F at the 5% level of significance?
What is the critical value of F at the 5% level of significance?A) 19.45
B) 3.00
C) 4.41
D) 4.38

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
26
When the null hypothesis for an ANOVA analysis comparing four treatment means, is rejected,
A) 2 comparisons of treatment means can be made.
B) 4 comparisons of treatment means can be made.
C) 6 comparisons of treatment means can be made.
D) 8 comparisons of treatment means can be made.
A) 2 comparisons of treatment means can be made.
B) 4 comparisons of treatment means can be made.
C) 6 comparisons of treatment means can be made.
D) 8 comparisons of treatment means can be made.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
27
When testing for differences between treatment means, a confidence interval is based on
A) the mean square error.
B) the standard deviation.
C) the sum of squared errors.
D) the standard error of the mean.
A) the mean square error.
B) the standard deviation.
C) the sum of squared errors.
D) the standard error of the mean.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
28
A preliminary study of hourly wages paid to unskilled employees in three metropolitan areas was conducted. Seven employees were included from Area A, 9 from Area B, and 12 from Area
A) Mean hourly wages of unskilled employees of all areas are equal
B) Mean hourly wages in at least 2 metropolitan areas are different
C) More degrees of freedom are needed
C) The test statistic was computed to be 4.91. What can we conclude at the 0.05 level?
D) None of these is correct
A) Mean hourly wages of unskilled employees of all areas are equal
B) Mean hourly wages in at least 2 metropolitan areas are different
C) More degrees of freedom are needed
C) The test statistic was computed to be 4.91. What can we conclude at the 0.05 level?
D) None of these is correct

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
29
Suppose a package delivery company purchased 14 trucks at the same time. Five trucks were purchased from manufacturer A, four from manufacturer B, and five from manufacturer
A) 2
B) 3
C) 11
C) The cost of maintaining each truck was recorded. The company used ANOVA to test if the mean maintenance cost of the trucks from each manufacturer were equal. To apply the F test, how many degrees of freedom must be in the denominator?
D) 14
A) 2
B) 3
C) 11
C) The cost of maintaining each truck was recorded. The company used ANOVA to test if the mean maintenance cost of the trucks from each manufacturer were equal. To apply the F test, how many degrees of freedom must be in the denominator?
D) 14

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
30
A manufacturer of automobile transmissions uses three different processes. Management ordered a study of the production costs to see if there is a difference among the three processes. A summary of the findings is shown below.  What are the total degrees of freedom?
What are the total degrees of freedom?
A) 27
B) 28
C) 29
D) 30
 What are the total degrees of freedom?
What are the total degrees of freedom?A) 27
B) 28
C) 29
D) 30

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
31
A manufacturer of automobile transmissions uses three different processes. Management ordered a study of the production costs to see if there is a difference among the three processes. A summary of the findings is shown below.  What are the degrees of freedom for the error sum of squares?
What are the degrees of freedom for the error sum of squares?
A) 3
B) 10
C) 27
D) 30
 What are the degrees of freedom for the error sum of squares?
What are the degrees of freedom for the error sum of squares?A) 3
B) 10
C) 27
D) 30

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
32
In ANOVA, an F statistic is used to test a null hypothesis such as: 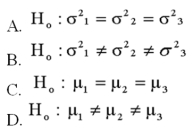
A) Option A
B) Option B
C) Option C
D) Option D
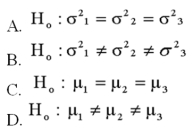
A) Option A
B) Option B
C) Option C
D) Option D

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
33
When testing for differences between treatment means, the degrees of freedom for the t statistic are:
A) k
B) (n - 1)
C) (n - k)
D) (1/n1 + 1/n2)
A) k
B) (n - 1)
C) (n - k)
D) (1/n1 + 1/n2)

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
34
Several employees have submitted different methods of assembling a subassembly. Sample data for each method are:  How many treatments are there?
How many treatments are there?
A) 3
B) 4
C) 12
D) 0
 How many treatments are there?
How many treatments are there?A) 3
B) 4
C) 12
D) 0

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
35
Given the following Analysis of Variance table for three treatments each with six observations.  What are the degrees of freedom for the treatment and error sum of squares?
What are the degrees of freedom for the treatment and error sum of squares?
A) 3 and 18
B) 2 and 17
C) 3 and 15
D) 2 and 15
 What are the degrees of freedom for the treatment and error sum of squares?
What are the degrees of freedom for the treatment and error sum of squares?A) 3 and 18
B) 2 and 17
C) 3 and 15
D) 2 and 15

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
36
A manufacturer of automobile transmissions uses two different processes. Management ordered a study of the production costs to see if there is a difference between the two processes. A summary of the findings is shown below. 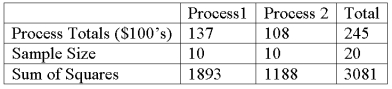 What is the critical value of F at the 1% level of significance?
What is the critical value of F at the 1% level of significance?
A) 9.46
B) 8.29
C) 8.18
D) 4.61
 What is the critical value of F at the 1% level of significance?
What is the critical value of F at the 1% level of significance?A) 9.46
B) 8.29
C) 8.18
D) 4.61

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
37
In ANOVA analysis, when the null hypothesis is rejected, we can test for differences between treatment means by
A) constructing confidence intervals.
B) adding another treatment.
C) doing an additional ANOVA.
D) doing a t test.
A) constructing confidence intervals.
B) adding another treatment.
C) doing an additional ANOVA.
D) doing a t test.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
38
An electronics company wants to compare the quality of their cell phones to the cell phones from three competitors. They sample 10 phones from each company and count the number of defects for each phone. If ANOVA were used to compare the average number of defects, then the treatments would be defined as:
A) The number of cell phones sampled.
B) The average number of defects.
C) The total number of phones.
D) The four companies.
A) The number of cell phones sampled.
B) The average number of defects.
C) The total number of phones.
D) The four companies.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
39
Three different fertilizers were applied to a field of celery. In computing F, how many degrees of freedom are there in the numerator?
A) 0
B) 1
C) 2
D) 3
A) 0
B) 1
C) 2
D) 3

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
40
An experiment to determine the most effective way to teach safety principles applied four different teaching methods. Some employees were given programmed instruction booklets and worked through the course at their own pace. Other employees attended lectures. A third group watched a television presentation, and a fourth group was divided into small discussion groups. A high of 10 was possible. A sample of five tests was selected from each group. The test grade results were: 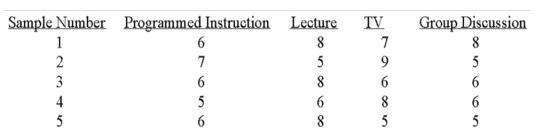 At the 0.01 level, what is the critical value?
At the 0.01 level, what is the critical value?
A) 1.00
B) 1.96
C) 3.24
D) 5.29
 At the 0.01 level, what is the critical value?
At the 0.01 level, what is the critical value?A) 1.00
B) 1.96
C) 3.24
D) 5.29

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
41
A random sample of 40 companies with assets over $10 million was selected and asked for their annual computer technology expense and industry. The ANOVA comparing the average computer technology expense among three industries rejected the null hypothesis. The Mean Square Error (MSE) was 195. The following table summarized the results:  Based on the comparison between the mean annual computer technology expense for companies in the Education and Tax services industries,
Based on the comparison between the mean annual computer technology expense for companies in the Education and Tax services industries,
A) A confidence interval shows that the mean annual computer technology expenses are not significantly different.
B) The ANOVA results show that the mean annual computer technology expenses are significantly different.
C) A confidence interval shows that the mean annual computer technology expenses are significantly different.
D) The ANOVA results show that the mean annual computer technology expenses are not significantly different.
 Based on the comparison between the mean annual computer technology expense for companies in the Education and Tax services industries,
Based on the comparison between the mean annual computer technology expense for companies in the Education and Tax services industries,A) A confidence interval shows that the mean annual computer technology expenses are not significantly different.
B) The ANOVA results show that the mean annual computer technology expenses are significantly different.
C) A confidence interval shows that the mean annual computer technology expenses are significantly different.
D) The ANOVA results show that the mean annual computer technology expenses are not significantly different.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
42
Two accounting professors decided to compare the variance of their grading procedures. To accomplish this, they each graded the same 10 exams with the following results:  What are the degrees of freedom for the numerator of the F ratio?
What are the degrees of freedom for the numerator of the F ratio?
A) 8
B) 9
C) 10
D) 18
 What are the degrees of freedom for the numerator of the F ratio?
What are the degrees of freedom for the numerator of the F ratio?A) 8
B) 9
C) 10
D) 18

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
43
Given the following Analysis of Variance table for three treatments each with six observations.  What is the critical value of F at the 5% level of significance?
What is the critical value of F at the 5% level of significance?
A) 3.29
B) 3.68
C) 3.59
D) 3.20
 What is the critical value of F at the 5% level of significance?
What is the critical value of F at the 5% level of significance?A) 3.29
B) 3.68
C) 3.59
D) 3.20

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
44
A random sample of 16 companies was selected and asked for their annual dividend rate in three different industries: utilities, banking, and insurance. The ANOVA comparing the mean annual dividend rate among three industries rejected the null hypothesis. The Mean Square Error (MSE) was 3.36. The following table summarized the results: 
When comparing the mean annual dividend rate for companies in the utilities and insurance industries, the following 95% confidence interval can be constructed:
A) 5.78 2.160 * 2.40
B) 5.78 2.120 * 2.40
C) 5.78 2.160 * 1.11
D) 5.78 2.120 * 1.11

When comparing the mean annual dividend rate for companies in the utilities and insurance industries, the following 95% confidence interval can be constructed:
A) 5.78 2.160 * 2.40
B) 5.78 2.120 * 2.40
C) 5.78 2.160 * 1.11
D) 5.78 2.120 * 1.11

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
45
Two accounting professors decided to compare the variance of their grading procedures. To accomplish this, they each graded the same 10 exams with the following results:  What are the degrees of freedom for the denominator of the F ratio?
What are the degrees of freedom for the denominator of the F ratio?
A) 20
B) 18
C) 10
D) 9
 What are the degrees of freedom for the denominator of the F ratio?
What are the degrees of freedom for the denominator of the F ratio?A) 20
B) 18
C) 10
D) 9

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
46
A random sample of 30 executives from companies with assets over $1 million was selected and asked for their annual income and level of education. The ANOVA comparing the average income among three levels of education rejected the null hypothesis. The Mean Square Error (MSE) was 243.7. The following table summarized the results:  Based on the comparison between the mean annual incomes for executives with Undergraduate and Master's Degree or more,
Based on the comparison between the mean annual incomes for executives with Undergraduate and Master's Degree or more,
A) A confidence interval shows that the mean annual incomes are not significantly different.
B) The ANOVA results show that the mean annual incomes are significantly different.
C) A confidence interval shows that the mean annual incomes are significantly different.
D) The ANOVA results show that the mean annual incomes are not significantly different.
 Based on the comparison between the mean annual incomes for executives with Undergraduate and Master's Degree or more,
Based on the comparison between the mean annual incomes for executives with Undergraduate and Master's Degree or more,A) A confidence interval shows that the mean annual incomes are not significantly different.
B) The ANOVA results show that the mean annual incomes are significantly different.
C) A confidence interval shows that the mean annual incomes are significantly different.
D) The ANOVA results show that the mean annual incomes are not significantly different.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
47
Two accounting professors decided to compare the variance of their grading procedures. To accomplish this, they each graded the same 10 exams with the following results:  What is H1?
What is H1? 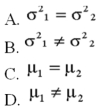
A) Option A
B) Option B
C) Option C
D) Option D
 What is H1?
What is H1? 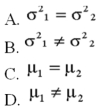
A) Option A
B) Option B
C) Option C
D) Option D

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
48
A random sample of 40 companies with assets over $10 million was selected and asked for their annual computer technology expense and industry. The ANOVA comparing the average computer technology expense among three industries rejected the null hypothesis. The Mean Square Error (MSE) was 195. The following table summarized the results:  Based on the comparison between the mean annual computer technology expense for companies in the Tax Service and Food Service industries, the 95% confidence interval shows an interval of -14.85 to 5.85 for the difference. This result indicates that
Based on the comparison between the mean annual computer technology expense for companies in the Tax Service and Food Service industries, the 95% confidence interval shows an interval of -14.85 to 5.85 for the difference. This result indicates that
A) There is no significant difference between the two expenses.
B) The interval contains a difference of 20.7.
C) Companies in the Tax Service industry spend significantly less than companies in the Food Service industry.
D) Companies in the Food Service industry spend significantly less than companies in the Tax Service industry.
 Based on the comparison between the mean annual computer technology expense for companies in the Tax Service and Food Service industries, the 95% confidence interval shows an interval of -14.85 to 5.85 for the difference. This result indicates that
Based on the comparison between the mean annual computer technology expense for companies in the Tax Service and Food Service industries, the 95% confidence interval shows an interval of -14.85 to 5.85 for the difference. This result indicates thatA) There is no significant difference between the two expenses.
B) The interval contains a difference of 20.7.
C) Companies in the Tax Service industry spend significantly less than companies in the Food Service industry.
D) Companies in the Food Service industry spend significantly less than companies in the Tax Service industry.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
49
Two accounting professors decided to compare the variance of their grading procedures. To accomplish this, they each graded the same 10 exams with the following results:  At the 1% level of significance, what is the decision?
At the 1% level of significance, what is the decision?
A) Reject the null hypothesis and conclude the variances are different.
B) Fail to reject the null hypothesis and conclude the variances are different.
C) Reject the null hypothesis and conclude the variances are the same.
D) Fail to reject the null hypothesis and conclude the variances are the same.
 At the 1% level of significance, what is the decision?
At the 1% level of significance, what is the decision?A) Reject the null hypothesis and conclude the variances are different.
B) Fail to reject the null hypothesis and conclude the variances are different.
C) Reject the null hypothesis and conclude the variances are the same.
D) Fail to reject the null hypothesis and conclude the variances are the same.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
50
Two accounting professors decided to compare the variance of their grading procedures. To accomplish this, they each graded the same 10 exams with the following results:  At the 5% level of significance, what is the decision regarding the null hypothesis?
At the 5% level of significance, what is the decision regarding the null hypothesis?
A) Reject the null hypothesis and conclude the variances are different.
B) Fail to reject the null hypothesis and conclude no significant difference in the variances.
C) Reject the null hypothesis and conclude the variances are the same.
D) Fail to reject the null hypothesis and conclude the variances are the same.
 At the 5% level of significance, what is the decision regarding the null hypothesis?
At the 5% level of significance, what is the decision regarding the null hypothesis?A) Reject the null hypothesis and conclude the variances are different.
B) Fail to reject the null hypothesis and conclude no significant difference in the variances.
C) Reject the null hypothesis and conclude the variances are the same.
D) Fail to reject the null hypothesis and conclude the variances are the same.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
51
A random sample of 40 companies with assets over $10 million was selected and asked for their annual computer technology expense and industry. The ANOVA comparing the average computer technology expense among three industries rejected the null hypothesis. The Mean Square Error (MSE) was 195. The following table summarized the results: 
When comparing the mean annual computer technology expense for companies in the Education and Tax services industries, the following 95% confidence interval can be constructed:
A) 13.5 2.026 * 5.78
B) 13.5 2.021 * 5.78
C) 13.5 2.026 * 13.96
D) 13.5 2.021 * 13.96

When comparing the mean annual computer technology expense for companies in the Education and Tax services industries, the following 95% confidence interval can be constructed:
A) 13.5 2.026 * 5.78
B) 13.5 2.021 * 5.78
C) 13.5 2.026 * 13.96
D) 13.5 2.021 * 13.96

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
52
A random sample of 30 executives from companies with assets over $1 million was selected and asked for their annual income and level of education. The ANOVA comparing the average income among three levels of education rejected the null hypothesis. The Mean Square Error (MSE) was 243.7. The following table summarized the results: 
When comparing the mean annual incomes for executives with Undergraduate and Master's Degree or more, the following 95% confidence interval can be constructed:
A) 2.0 2.052 * 6.51
B) 2.0 3.182 * 6.51
C) 2.0 2.052 * 42.46
D) 2.0 3.182 * 42.46

When comparing the mean annual incomes for executives with Undergraduate and Master's Degree or more, the following 95% confidence interval can be constructed:
A) 2.0 2.052 * 6.51
B) 2.0 3.182 * 6.51
C) 2.0 2.052 * 42.46
D) 2.0 3.182 * 42.46

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
53
Two accounting professors decided to compare the variance of their grading procedures. To accomplish this, they each graded the same 10 exams with the following results:  What is the critical value of F at the 0.01 level of significance?
What is the critical value of F at the 0.01 level of significance?
A) 5.85
B) 5.35
C) 6.51
D) 4.03
 What is the critical value of F at the 0.01 level of significance?
What is the critical value of F at the 0.01 level of significance?A) 5.85
B) 5.35
C) 6.51
D) 4.03

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
54
Two accounting professors decided to compare the variance of their grading procedures. To accomplish this, they each graded the same 10 exams with the following results:  The calculated F ratio is
The calculated F ratio is
A) 3.484
B) 1.867
C) 3.18
D) 5.35
 The calculated F ratio is
The calculated F ratio isA) 3.484
B) 1.867
C) 3.18
D) 5.35

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
55
Two accounting professors decided to compare the variance of their grading procedures. To accomplish this, they each graded the same 10 exams with the following results:  What is H0?
What is H0? 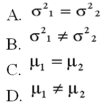
A) Option A
B) Option B
C) Option C
D) Option D
 What is H0?
What is H0? 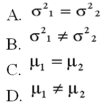
A) Option A
B) Option B
C) Option C
D) Option D

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
56
A random sample of 30 executives from companies with assets over $1 million was selected and asked for their annual income and level of education. The ANOVA comparing the average income among three levels of education rejected the null hypothesis. The Mean Square Error (MSE) was 243.7. The following table summarized the results: 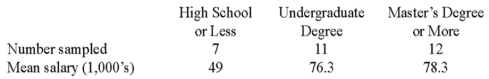 When comparing the mean annual incomes for executives with a High School education or less and Undergraduate Degree, the 95% confidence interval shows an interval of 11.7 to 42.7 for the difference. This result indicates that
When comparing the mean annual incomes for executives with a High School education or less and Undergraduate Degree, the 95% confidence interval shows an interval of 11.7 to 42.7 for the difference. This result indicates that
A) There is no significant difference between the two incomes.
B) The interval contains a difference of zero.
C) Executives with an Undergraduate Degree earn significantly more than executives with a High School education or less.
D) Executives with an Undergraduate Degree earn significantly less than executives with a High School education or less.
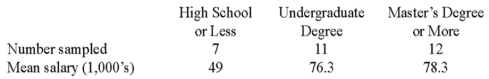 When comparing the mean annual incomes for executives with a High School education or less and Undergraduate Degree, the 95% confidence interval shows an interval of 11.7 to 42.7 for the difference. This result indicates that
When comparing the mean annual incomes for executives with a High School education or less and Undergraduate Degree, the 95% confidence interval shows an interval of 11.7 to 42.7 for the difference. This result indicates thatA) There is no significant difference between the two incomes.
B) The interval contains a difference of zero.
C) Executives with an Undergraduate Degree earn significantly more than executives with a High School education or less.
D) Executives with an Undergraduate Degree earn significantly less than executives with a High School education or less.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
57
Given the following Analysis of Variance table for three treatments each with six observations.  What is the decision regarding the null hypothesis?
What is the decision regarding the null hypothesis?
A) Reject H0 - there is a difference in treatment means
B) Fail to reject H0 - there is a difference in treatment means
C) Reject H0 - there is a difference in errors
D) Fail to reject H0 - there is a difference in errors
 What is the decision regarding the null hypothesis?
What is the decision regarding the null hypothesis?A) Reject H0 - there is a difference in treatment means
B) Fail to reject H0 - there is a difference in treatment means
C) Reject H0 - there is a difference in errors
D) Fail to reject H0 - there is a difference in errors

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
58
Given the following Analysis of Variance table for three treatments each with six observations.  What is the computed value of F?
What is the computed value of F?
A) 7.48
B) 7.84
C) 8.84
D) 8.48
 What is the computed value of F?
What is the computed value of F?A) 7.48
B) 7.84
C) 8.84
D) 8.48

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
59
Given the following Analysis of Variance table for three treatments each with six observations.  What is the mean square for treatments?
What is the mean square for treatments?
A) 71.2
B) 71.4
C) 558
D) 534
 What is the mean square for treatments?
What is the mean square for treatments?A) 71.2
B) 71.4
C) 558
D) 534

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
60
Two accounting professors decided to compare the variance of their grading procedures. To accomplish this, they each graded the same 10 exams with the following results:  What is the critical value of F at the 0.05 level of significance?
What is the critical value of F at the 0.05 level of significance?
A) 5.85
B) 5.35
C) 3.18
D) 4.03
 What is the critical value of F at the 0.05 level of significance?
What is the critical value of F at the 0.05 level of significance?A) 5.85
B) 5.35
C) 3.18
D) 4.03

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
61
The college of business was interested in comparing the interaction of Academic status and class time on class attendance. Three different classes were sampled for each cell in the table. The means for each cell follow. 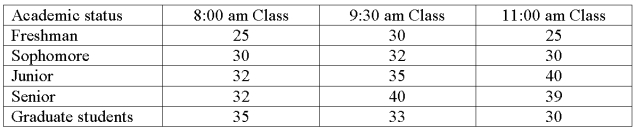 What are the total degrees of freedom?
What are the total degrees of freedom?
A) 44.
B) 14.
C) 4.
D) 2.
 What are the total degrees of freedom?
What are the total degrees of freedom?A) 44.
B) 14.
C) 4.
D) 2.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
62
If there are 5 levels of Factor A and 7 levels of Factor B for an ANOVA with interaction, what are the interaction degrees of freedom?
A) 12.
B) 35.
C) 24.
D) 10.
A) 12.
B) 35.
C) 24.
D) 10.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
63
The college of business was interested in comparing the attendance for three different class times for a business statistics class. The data follow. 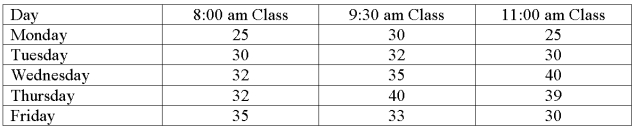 What is the blocking variable?
What is the blocking variable?
A) Day.
B) Class time.
C) Tuesday.
D) 8:00 am class.
 What is the blocking variable?
What is the blocking variable?A) Day.
B) Class time.
C) Tuesday.
D) 8:00 am class.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
64
The F distribution is a ______________ distribution.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
65
The college of business was interested in comparing the attendance for three different class times for a business statistics class. The data follow. 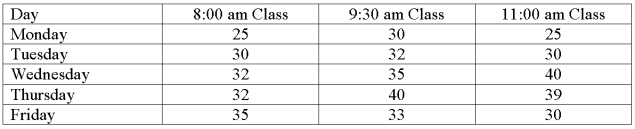 What is the treatment variable?
What is the treatment variable?
A) Day.
B) Class time.
C) Tuesday.
D) 8:00 am class.
 What is the treatment variable?
What is the treatment variable?A) Day.
B) Class time.
C) Tuesday.
D) 8:00 am class.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
66
What are the minimum and maximum of values of an F distribution? _______ and _______

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
67
All values in an F distribution must be _____________.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
68
In a two-way ANOVA, the sources of variation are
A) Total variation and error variation.
B) Total variation, treatment variation, and error variation.
C) Total variation, treatment variation, blocking variation and error variation.
D) Treatment variation and blocking variation.
A) Total variation and error variation.
B) Total variation, treatment variation, and error variation.
C) Total variation, treatment variation, blocking variation and error variation.
D) Treatment variation and blocking variation.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
69
The college of business was interested in comparing the interaction of Academic status and class time on class attendance. Three different classes were sampled for each cell in the table. The means for each cell follow. 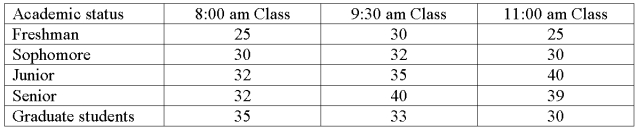 What are the interaction degrees of freedom?
What are the interaction degrees of freedom?
A) 10.
B) 2.
C) 4.
D) 8.
 What are the interaction degrees of freedom?
What are the interaction degrees of freedom?A) 10.
B) 2.
C) 4.
D) 8.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
70
The college of business was interested in comparing the interaction of Academic status and class time on class attendance. Three different classes were sampled for each cell in the table. The means for each cell follow. 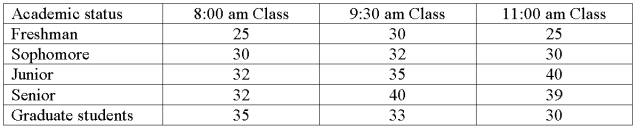 What are the error degrees of freedom?
What are the error degrees of freedom?
A) 44.
B) 14.
C) 30.
D) 2.
 What are the error degrees of freedom?
What are the error degrees of freedom?A) 44.
B) 14.
C) 30.
D) 2.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
71
The college of business was interested in comparing the attendance for three different class times for a business statistics class. The data follow. 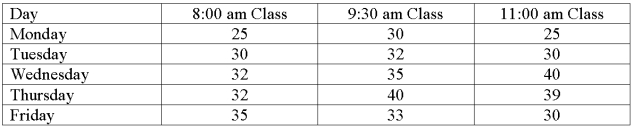 What are the block and treatment degrees of freedom?
What are the block and treatment degrees of freedom?
A) 5 and 3.
B) 5 and 5.
C) 4 and 2.
D) 3 and 15.
 What are the block and treatment degrees of freedom?
What are the block and treatment degrees of freedom?A) 5 and 3.
B) 5 and 5.
C) 4 and 2.
D) 3 and 15.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
72
A random sample of 16 companies was selected and asked for their annual dividend rate in three different industries: utilities, banking, and insurance. The ANOVA comparing the mean annual dividend rate among three industries rejected the null hypothesis. The Mean Square Error (MSE) was 3.36. The following table summarized the results:  Based on the comparison between the mean annual dividend rate for companies in the utilities and banking, the 95% confidence interval shows an interval of 1.28 to 6.28 for the difference. This result indicates that
Based on the comparison between the mean annual dividend rate for companies in the utilities and banking, the 95% confidence interval shows an interval of 1.28 to 6.28 for the difference. This result indicates that
A) There is no significant difference between the two rates.
B) The interval contains a difference of 5.00.
C) The annual dividend rate in the utilities industry is significantly less than the annual dividend rate in banking industry.
D) The annual dividend rate in banking industry is significantly less than the annual dividend rate in utilities industry.
 Based on the comparison between the mean annual dividend rate for companies in the utilities and banking, the 95% confidence interval shows an interval of 1.28 to 6.28 for the difference. This result indicates that
Based on the comparison between the mean annual dividend rate for companies in the utilities and banking, the 95% confidence interval shows an interval of 1.28 to 6.28 for the difference. This result indicates thatA) There is no significant difference between the two rates.
B) The interval contains a difference of 5.00.
C) The annual dividend rate in the utilities industry is significantly less than the annual dividend rate in banking industry.
D) The annual dividend rate in banking industry is significantly less than the annual dividend rate in utilities industry.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
73
What test statistic is used to compare two variances? ________________

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
74
In a two-way ANOVA, a blocking variable is used to
A) increase the error sum of squares.
B) decrease the error sum of squares.
C) increase the treatment sum of squares.
D) decrease the treatment sum of squares.
A) increase the error sum of squares.
B) decrease the error sum of squares.
C) increase the treatment sum of squares.
D) decrease the treatment sum of squares.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
75
What is the shape of the F distribution? ______________________

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
76
The college of business was interested in comparing the attendance for three different class times for a business statistics class. The data follow. 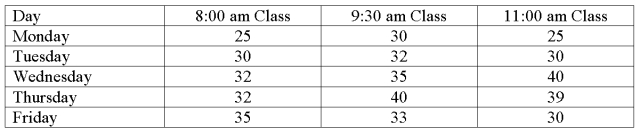 What is the critical F statistic for testing the hypothesis of equal treatment means at the 0.05 significance level?
What is the critical F statistic for testing the hypothesis of equal treatment means at the 0.05 significance level?
A) 1.96.
B) 6.94.
C) 3.84.
D) 4.46.
 What is the critical F statistic for testing the hypothesis of equal treatment means at the 0.05 significance level?
What is the critical F statistic for testing the hypothesis of equal treatment means at the 0.05 significance level?A) 1.96.
B) 6.94.
C) 3.84.
D) 4.46.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
77
In a two-way ANOVA with interaction, a significant interaction term indicates that
A) the response variable is interactive.
B) a blocking factor is present.
C) both factors are unrelated.
D) both factors have a combined effect on the response variable.
A) the response variable is interactive.
B) a blocking factor is present.
C) both factors are unrelated.
D) both factors have a combined effect on the response variable.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
78
A two-way ANOVA with interaction has how many sources of variation?
A) 5.
B) 4.
C) 3.
D) 2.
A) 5.
B) 4.
C) 3.
D) 2.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
79
A random sample of 16 companies was selected and asked for their annual dividend rate in three different industries: utilities, banking, and insurance. The ANOVA comparing the mean annual dividend rate among three industries rejected the null hypothesis. The Mean Square Error (MSE) was 3.36. The following table summarized the results:  Based on the comparison between the mean annual dividend rate for companies in the utilities and insurance industries,
Based on the comparison between the mean annual dividend rate for companies in the utilities and insurance industries,
A) A confidence interval shows that the mean annual dividend rates are not significantly different.
B) The ANOVA results show that the mean annual dividend rates are significantly different.
C) A confidence interval shows that the mean annual dividend rates are significantly different.
D) The ANOVA results show that the mean annual dividend rates are not significantly different.
 Based on the comparison between the mean annual dividend rate for companies in the utilities and insurance industries,
Based on the comparison between the mean annual dividend rate for companies in the utilities and insurance industries,A) A confidence interval shows that the mean annual dividend rates are not significantly different.
B) The ANOVA results show that the mean annual dividend rates are significantly different.
C) A confidence interval shows that the mean annual dividend rates are significantly different.
D) The ANOVA results show that the mean annual dividend rates are not significantly different.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
80
The F-distribution is useful when testing a requirement of two-sample tests of hypothesis. What is the assumption? ________________

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck


