Deck 11: Two-Sample Tests of Hypothesis

Question 1

If we are testing for the difference between two population proportions, it is assumed that the two populations are approximately normal and have equal variances.

Answer 1

False

Question 2

A statistics professor wants to compare grades in two different classes of the same course. This is an example of a paired sample.

Answer 2

False

Question 3

When the standard deviations are equal but unknown, a test for the differences between two population means has n - 1 degrees of freedom.

Answer 3

False

Question 4

If the null hypothesis states that there is no difference between the mean net income of retail stores in Chicago and New York City, then the test is two-tailed.

Question 5

If two independent samples of size 10 with unequal standard deviations are used to test the difference between the means, the degrees of freedom for a t-statistic are 18.

Question 6

A recent study focused on the number of times men and women send a Twitter message in a day. The information is summarized below. At the .01 significance level, is there a difference in the mean number of times men and women send a Twitter message in a day? What is the value of the test statistic for this hypothesis test?

A) 2.668
B) 2.672
C) 2.58
D) 2.40

Question 7

In testing the difference between two population proportions, we pool the two sample proportions to estimate the population proportion.

Question 8

A recent study focused on the number of times men and women send a Twitter message in a day. The information is summarized below. At the .01 significance level, is there a difference in the mean number of times men and women in a day? What is the test statistic for this hypothesis?

A) z-statistic
B) t-statistic
C) p-statistic
D) df-statistic

Question 9

If we are testing for the difference between two population means, it is assumed that the sample observations from one population are independent of the sample observations from the other population.

Question 10

When dependent samples are used to test for differences in the means, we compute paired differences.

Question 11

When independent samples, with unknown, unequal standard deviations, are used to test for differences in the means, we pool the sample variances.

Question 12

A recent study focused on the number of times men and women send a Twitter message in a day. The information is summarized below. At the .01 significance level, is there a difference in the mean number of times men and women send a Twitter message in a day? What is the p-value hypothesis test?

A) 0.05
B) 0.0164
C) 0.0001
D) 0.0082

Question 13

If the null hypothesis states that there is no difference between the mean income of males and the mean income of females, then the test is one-tailed.

Question 14

If the decision is to reject the null hypothesis of no difference between two population proportions at the 5% level of significance, what are the alternative hypothesis and rejection region?

A) H₀: $\pi$ ₁ $\neq$ $\pi$ ₂; z > 1.65 and z < -1.65
B) H₀: $\pi$ ₁ $\neq$$\pi$ ₂; z > 1.96 and z < -1.96
C) H₀: $\pi$ ₁ > $\pi$ ₂; z < - 1.65
D) H₀: $\pi$ ₁ > $\pi$ ₂; z < -1.96F

Question 15

If two dependent samples of size 20 are used to test the difference between the means, the degrees of freedom for a t-statistic are 19.

Question 16

If we are testing for the difference between two population means and assume that the two populations have equal and unknown standard deviations, the degrees of freedom are computed as (n₁)(n₂) - 1.

Question 17

The pooled estimate of the proportion is found by dividing the total number of samples by the total number of successes.

Question 18

In a market test of a new chocolate raspberry coffee, a poll of 400 people from Dobbs Ferry showed 250 preferred the new coffee. In Irvington, 170 out of 350 people preferred the new coffee. To test the hypothesis that there is no difference in preferences between the two villages, what is the alternate hypothesis?

A) H₁: $\pi$ ₁ < $\pi$ ₂
B) H₁: $\pi$ ₁ > $\pi$ ₂
C) H₁: $\pi$ ₁ = $\pi$ ₂
D) H₁: $\pi$ ₁ $\neq$$\pi$ ₂

Question 19

If we are testing for the difference between two population means and assume that the two populations have equal but unknown standard deviations, the variances are pooled to compute the best estimated variance.

Question 20

When dependent samples are used to test for differences in the means, we pool the sample variances.

Question 21

The net weights (in grams) of a sample of bottles filled by a machine manufactured by Edne, and the net weights of a sample filled by a similar machine manufactured by Orno, Inc., are: Edne: 5, 8, 7, 6, 9 and 7
Orno: 8, 10, 7, 11, 9, 12, 14 and 9
Testing the claim at the 0.05 level that the mean weight of the bottles filled by the Orno machine is greater than the mean weight of the bottles filled by the Edne machine, what is the critical value? Assume equal standard deviations for both samples.

A) 2.179
B) 2.145
C) 1.782
D) 1.761

Question 22

A recent study focused on the amount of money single men and women save monthly. The information is summarized below. Assume that the population standard deviations are equal. At the .01 significance level, do women save more money than men? What is the value of the critical value for this hypothesis test?

A) 6.213
B) 2.369
C) 2.632
D) 2.40

Question 23

When testing the difference between two population means, the variances are pooled when

A) the population standard deviations are known and equal.
B) the population means are known.
C) the population standard deviations are assumed unequal and unknown.
D) the population standard deviations are assumed equal but unknown.

Question 24

For a hypothesis comparing two population means, what is the critical value for a one-tailed hypothesis test, using a 5% level of significance level, with both sample sizes equal to 13? Assume the population standard deviations are equal.

A) 1.708
B) 1.711
C) 2.060
D) 2.064

Question 25

When testing the difference between two dependent population means, the test statistic is based on a

A) pooled variance.
B) standard deviation of the differences.
C) pooled proportion.
D) sum of the population variances.

Question 26

If the null hypothesis that two means are equal is true, where will 97% of the computed z-values lie between?

A) $\pm$ 2.58
B) $\pm$ 2.33
C) $\pm$ 2.17
D) $\pm$ 2.07

Question 27

In a market test of a new chocolate raspberry coffee, a poll of 400 people (sample 1) from Dobbs Ferry showed 250 preferred the new coffee. In Irvington, 170 (sample 2) out of 350 people preferred the new coffee. To test the hypothesis that a higher proportion of people in Dobbs Ferry prefer the new coffee, what is the alternate hypothesis?

A) H₁: $\pi$ ₁ < $\pi$ ₂
B) H₁: $\pi$ ₁ > $\pi$ ₂
C) H₁: $\pi$ ₁ = $\pi$ ₂
D) H₁: $\pi$ ₁ $\neq$ $\pi$ ₂

Question 28

Administering the same test to a group of 15 students and a second group of 15 students to see which group scores higher is an example of

A) a one sample test of means.
B) a two sample test of means.
C) a paired t-test.
D) a test of proportions.

Question 29

Assuming the population variances are known, the population variance of the difference between two sample means is

A) the sum of the two means.
B) the sum of the variances for each population.
C) the sum of the standard deviations for each population.
D) the sum of the sample sizes for each population.

Question 30

A recent study focused on the amount of money single men and women save monthly. The information is summarized below. Assume that the population standard deviations are equal. At the .01 significance level, do women save more money than men? What is the test statistic for this hypothesis?

A) z-statistic
B) t-statistic
C) p-statistic
D) df-statistic

Question 31

A recent study focused on the number of times men and women send a Twitter message in a day. The information is summarized below. At the .01 significance level, is there a difference in the mean number of times men and women send a Twitter message in a day? What is the p-value hypothesis test?

A) Reject the null hypothesis and conclude the means are different.
B) Reject the null hypothesis and conclude the means are the same.
C) Fail to reject the null hypothesis and conclude the means are the same.
D) Fail to reject the null hypothesis and conclude the means are different.

Question 32

When testing the difference between two population means, the degrees of freedom must be computed when

A) the population standard deviations are known and equal.
B) the population means are known.
C) the population standard deviations are assumed unequal and unknown.
D) the population standard deviations are assumed equal but unknown.

Question 33

Using two independent samples, we test for a hypothesized difference between two population means. The population standard deviations are unknown but assumed equal. The number in the first sample is fifteen and the number in the second sample is twelve. How many degrees of freedom are associated with the critical value?

A) 24
B) 25
C) 26
D) 27

Question 34

A recent study focused on the amount of money single men and women save monthly. The information is summarized below. Assume that the population standard deviations are equal. At the .01 significance level, do women save more money than men? What is the value of the test statistic for this hypothesis test?

A) 6.213
B) 1.728
C) 2.632
D) 2.40

Question 35

How is a pooled estimate of the population proportion represented?

A) p_c
B) z
C) $\pi$
D) n $\pi$

Question 36

A recent study focused on the amount of money single men and women save monthly. The information is summarized below. Assume that the population standard deviations are equal. At the .01 significance level, do women save more money than men?

A) Reject the null hypothesis and conclude that women save more than men.
B) Reject the null hypothesis and conclude that women and men save the same amount.
C) Fail to reject the null hypothesis and conclude that women save the same or less than men.
D) Fail to reject the null hypothesis and conclude the means are different.

Question 37

For a hypothesis comparing two population means, what is the critical value for a one-tailed hypothesis test, using a 5% level of significance level, with both sample sizes equal to 13? The standard deviations for the samples are 5 and 7. Assume the population standard deviations are unequal.

A) 2.064
B) 1.711
C) 2.074
D) 1.717

Question 38

Which condition must be met to conduct a test for the difference in two sample means using a z-statistic?

A) Data must be at least of nominal scale
B) Populations must be normal
C) Standard deviations of the two populations must be known
D) Samples are dependent

Question 39

Suppose we test the difference between two proportions at the 0.05 level of significance. If the z test statistic is -1.07, what is our decision?

A) Reject the null hypothesis
B) Do not reject the null hypothesis
C) Take a larger sample
D) Reserve judgment

Question 40

When is it appropriate to use the paired difference t-test?

A) Four samples are compared at once
B) Any two samples are compared
C) Two independent samples are compared
D) Two dependent samples are compared

Question 41

Of 250 adults who tried a new multi-grain cereal, "Wow!", 187 rated it excellent; of 100 children sampled, 66 rated it excellent. What is the pooled proportion?

A) 0.723
B) 1.408
C) 0.494
D) 0.807

Question 42

Accounting procedures allow a business to evaluate their inventory at LIFO (Last In First Out) or FIFO (First In First Out). A manufacturer evaluated its finished goods inventory (in $ thousands) for five products both ways. Based on the following results, is LIFO more effective in keeping the value of his inventory lower?
What is the null hypothesis?

A) H₀: µ_F = µ_L
B) H₀: µ_F $\neq$ µ_L
C) H₀: µ_F $\le$ µ_L
D) H₀: µ_F $\ge$ µ_L

Question 43

A national manufacturer of ball bearings is experimenting with two different processes for producing precision ball bearings. It is important that the diameters be as close as possible to an industry standard. The output from each process is sampled and the average error from the industry standard is calculated. The results are presented below. The researcher is interested in determining whether there is evidence that the two processes yield different average errors. Assume that the population standard deviations are equal. What is the computed value of t?

A) +2.797
B) -2.797
C) -13.70
D) +13.70

Question 44

An investigation of the effectiveness of a training program to improve customer relationships included a pre-training and post-training customer survey. Seven customers were randomly selected and completed both surveys. The results follow. 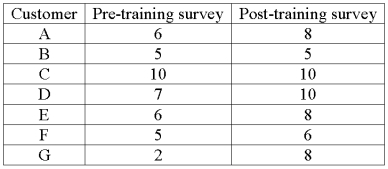This analysis is an example of

A) a one sample test of means.
B) a two sample test of means.
C) a paired t-test.
D) a test of proportions.

Question 45

The results of a mathematics placement exam at two different campuses of Mercy College follow: Given that the two population standard deviations are known, what is the p-value?

A) 1.0
B) 0.0
C) 0.05
D) 0.95

Question 46

Of 250 adults who tried a new multi-grain cereal, "Wow!", 187 rated it excellent; of 100 children sampled, 66 rated it excellent. Using the 0.1 significance level and the alternate hypothesis $\pi$ ₁
not equal to $\pi$ ₂
, what is the null hypothesis?

A) H₀: $\pi$ ₁ > $\pi$ ₂
B) H₀: $\pi$ ₁ < $\pi$ ₂
C) H₀: $\pi$ ₁ = $\pi$ ₂
D) H₀: $\pi$ ₁ $\neq$$\pi$ ₂

Question 47

A national manufacturer of ball bearings is experimenting with two different processes for producing precision ball bearings. It is important that the diameters be as close as possible to an industry standard. The output from each process is sampled and the average error from the industry standard is calculated. The results are presented below.
The researcher is interested in determining whether there is evidence that the two processes yield different average errors. Assume that the population standard deviations are equal. What is the critical t value at the 1% level of significance?

A) +2.779
B) -2.492
C) $\pm$ 1.711
D) $\pm$ 2.797

Question 48

A national manufacturer of ball bearings is experimenting with two different processes for producing precision ball bearings. It is important that the diameters be as close as possible to an industry standard. The output from each process is sampled and the average error from the industry standard is calculated. The results are presented below.
The researcher is interested in determining whether there is evidence that the two processes yield different average errors. Assume that the population standard deviations are equal. What is the null hypothesis?

A) H₀: µ_A = µ_B
B) H₀: µ_A $\neq$ µ_B
C) H₀: µ_A $\le$ µ_B
D) H₀: µ_A > µ_B

Question 49

20 randomly selected statistics students were given 15 multiple-choice questions and 15 open-ended questions - all on the same material. The professor was interested in determining which type of questions the students scored higher. This experiment is an example of

A) a one sample test of means.
B) a two sample test of means.
C) a paired t-test.
D) a test of proportions.

Question 50

Two samples, one of size 14 and the second of size 13, are selected to test the difference between two population means. How many degrees of freedom are used to find the critical value? Assume the population standard deviations are equal.

A) 27
B) 26
C) 25
D) 14
E) 13

Question 51

A national manufacturer of ball bearings is experimenting with two different processes for producing precision ball bearings. It is important that the diameters be as close as possible to an industry standard. The output from each process is sampled and the average error from the industry standard is calculated. The results are presented below. The researcher is interested in determining whether there is evidence that the two processes yield different average errors. Assume that the population standard deviations are equal. This example is what type of test?

A) One sample test of means.
B) Two sample test of means.
C) Paired t-test.
D) Test of proportions.

Question 52

The results of a mathematics placement exam at two different campuses of Mercy College follow:
What is the alternative hypothesis if we want to test the hypothesis that the mean score on Campus 1 is higher than on Campus 2?

A) H₀: µ₁ = 0
B) H₀: µ₂ = 0
C) H₀: µ₁ > µ₂
D) H₀: µ₁ $\le$ µ₂

Question 53

A national manufacturer of ball bearings is experimenting with two different processes for producing precision ball bearings. It is important that the diameters be as close as possible to an industry standard. The output from each process is sampled and the average error from the industry standard is calculated. The results are presented below. The researcher is interested in determining whether there is evidence that the two processes yield different average errors. Assume that the population standard deviations are equal. If we test the null hypothesis at the 1% level of significance, what is the decision?

A) Reject the null hypothesis and conclude the means are different.
B) Reject the null hypothesis and conclude the means are the same.
C) Fail to reject the null hypothesis and conclude the means are the same.
D) Fail to reject the null hypothesis and conclude the means are different.

Question 54

A national manufacturer of ball bearings is experimenting with two different processes for producing precision ball bearings. It is important that the diameters be as close as possible to an industry standard. The output from each process is sampled and the average error from the industry standard is calculated. The results are presented below.
The researcher is interested in determining whether there is evidence that the two processes yield different average errors. Assume that the population standard deviations are equal. What is the alternate hypothesis?

A) H₀: µ_A = µ_B
B) H₀: µ_A $\neq$ µ_B
C) H₀: µ_A $\le$ µ_B
D) H₀: µ_A > µ_B

Question 55

A national manufacturer of ball bearings is experimenting with two different processes for producing precision ball bearings. It is important that the diameters be as close as possible to an industry standard. The output from each process is sampled and the average error from the industry standard is calculated. The results are presented below. The researcher is interested in determining whether there is evidence that the two processes yield different average errors. Assume that the population standard deviations are equal. What is the degrees of freedom?

A) 10
B) 13
C) 26
D) 24

Question 56

For a hypothesis test comparing two population means, the combined degrees of freedom are 24. Which of the following statements about the two sample sizes is NOT true? Assume the population standard deviations are equal.

A) n₁ = 11; n₂= 13
B) n₁= 12; n₂= 14
C) n₁= 13; n₂= 13
D) n₁= 10; n₂= 16

Question 57

The results of a mathematics placement exam at two different campuses of Mercy College follow: What is the computed value of the test statistic?

A) 9.3
B) 2.6
C) 3.4
D) 1.9

Question 58

Of 250 adults who tried a new multi-grain cereal, "Wow!", 187 rated it excellent; of 100 children sampled, 66 rated it excellent. What test statistic should we use to compare the ratings of adults and children?

A) z-statistic
B) Right one-tailed test
C) Left one-tailed test
D) Two-tailed test

Question 59

The results of a mathematics placement exam at two different campuses of Mercy College follow:
What is the null hypothesis if we want to test the hypothesis that the mean score on Campus 1 is higher than on Campus 2?

A) H₀: µ₁ = 0
B) H₀: µ₂ = 0
C) H₀: µ₁ = µ₂
D) H₀: µ₁ $\le$ µ₂

Question 60

Accounting procedures allow a business to evaluate their inventory at LIFO (Last In First Out) or FIFO (First In First Out). A manufacturer evaluated its finished goods inventory (in $ thousands) for five products both ways. Based on the following results, is LIFO more effective in keeping the value of his inventory lower?
What is the alternate hypothesis?

A) H₁: µ_F = µ_L
B) H₁: µ_F $neq$ µ_L
C) H₁: µ_F $\le$ µ_L
D) H₁: µ_F > µ_L

Question 61

Accounting procedures allow a business to evaluate their inventory at LIFO (Last In First Out) or FIFO (First In First Out). A manufacturer evaluated its finished goods inventory (in $ thousands) for five products both ways. Based on the following results, is LIFO more effective in keeping the value of his inventory lower?
What is the value of calculated t?

A) +0.933
B) $\pm$ 2.776
C) +0.47
D) -2.028

Question 62

A hypothesis tests that two population means are equal. A sample of 10 with a standard deviation of 5 is selected from the first population and a sample of 15 with a standard deviation of 5 from the second population. Testing the claim at the 0.01 level, what is the critical value? Assume unequal standard deviations.

A) $\pm$ 2.861
B) $\pm$ 2.807
C) $\pm$ 2.787
D) $\pm$ 2.576

Question 63

Accounting procedures allow a business to evaluate their inventory at LIFO (Last In First Out) or FIFO (First In First Out). A manufacturer evaluated its finished goods inventory (in $ thousands) for five products both ways. Based on the following results, is LIFO more effective in keeping the value of his inventory lower? What is the decision at the 5% level of significance?

A) Fail to reject the null hypothesis and conclude LIFO is more effective.
B) Reject the null hypothesis and conclude LIFO is more effective.
C) Reject the alternate hypothesis and conclude LIFO is more effective.
D) Fail to reject the null hypothesis and conclude LIFO is not more effective.

Question 64

If we are testing for the difference between two population proportions, it is assumed that the two samples are large enough that the binomial distribution can be approximated by _____.

Question 65

A company is researching the effectiveness of a new web site design to decrease the time to access a website. Five web site users were randomly selected and their times (in seconds) to access the web site with the old and new designs were recorded. The results follow.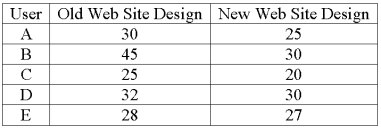
What is the null hypothesis?

A) H₀: µ_d = 0
B) H₀: µ_d $\neq$ 0
C) H₀: µ_d $\le$ 0
D) H₀: µ_d $\ge$ 0

Question 66

Accounting procedures allow a business to evaluate their inventory at LIFO (Last In First Out) or FIFO (First In First Out). A manufacturer evaluated its finished goods inventory (in $ thousands) for five products both ways. Based on the following results, is LIFO more effective in keeping the value of his inventory lower? This example is what type of test?

A) One sample test of means.
B) Two sample test of means.
C) Paired t-test.
D) Test of proportions.

Question 67

What is the purpose of pooling the sample proportions when testing the difference between two population proportions? ___________

Question 68

When testing the hypothesized difference between two population means, the implied hypothesis is

A) H₀: µ₁ = 0
B) H₀: µ₁ - µ₂ = 0
C) H₀: µ₂ = 0
D) H₀: µ₁ - µ₂ $\neq$ 0

Question 69

A study by a bank compared the average savings of customers who were depositors for three years or less, with those who had been depositors for more than three years. The results of a sample are: 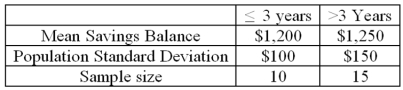Assuming that the financial officer wants to show that there is a difference in the average savings balance between the two classes of depositors, what is the null hypothesis? _____________________

Question 70

A company is researching the effectiveness of a new web site design to decrease the time to access a website. Five web site users were randomly selected and their times (in seconds) to access the web site with the old and new designs were recorded. The results follow. 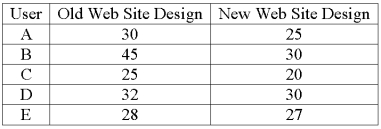For a 0.01 significance level, what is the critical value?

A) 2.256
B) 1.895
C) 3.747
D) 2.447

Question 71

An investigation of the effectiveness of a training program to improve customer relationships included a pre-training and post-training customer survey. Seven customers were randomly selected and completed both surveys. The results follow. 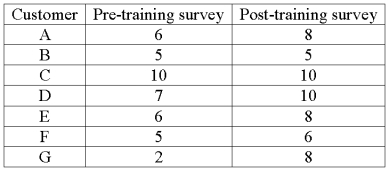For a 0.05 significance level, what is the decision regarding the hypothesis that the training was effective in improving customer relationships?

A) Reject the null hypothesis and conclude that the training was effective.
B) Reject the null hypothesis and conclude that the training was ineffective.
C) Fail to reject the null hypothesis and conclude that mean survey scores are the same.
D) Fail to reject the null hypothesis and conclude that the mean survey scores are not equal.

Question 72

An investigation of the effectiveness of a training program to improve customer relationships included a pre-training and post-training customer survey. Seven customers were randomly selected and completed both surveys. The results follow. 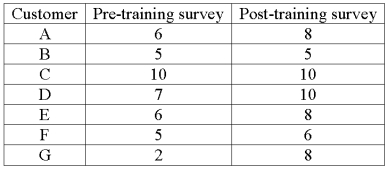For a 0.05 significance level, what is the critical value?

A) 1.943
B) 1.895
C) 1.645
D) 2.447

Question 73

When the population standard deviations are unknown, what is the purpose of pooling the sample variances when testing the difference between two population means? ___________

Question 74

A company is researching the effectiveness of a new web site design to decrease the time to access a website. Five web site users were randomly selected and their times (in seconds) to access the web site with the old and new designs were recorded. The results follow. 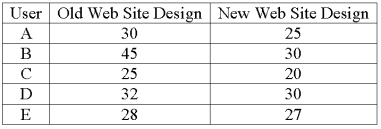For a 0.01 significance level, what is the decision regarding the hypothesis that the training was effective in improving customer relationships?

A) Reject the null hypothesis and conclude that the new design reduced mean access times.
B) Reject the null hypothesis and conclude that the new design did not reduce mean access times. Fail to reject the null hypothesis and conclude that mean access times did not decrease.
D) Fail to reject the null hypothesis and conclude that the mean access times are inaccurate.

Question 75

The pooled estimate of the proportion is found by dividing the total number of successes by __________________________.

Question 76

An investigation of the effectiveness of a training program to improve customer relationships included a pre-training and post-training customer survey. Seven customers were randomly selected and completed both surveys. The results follow. 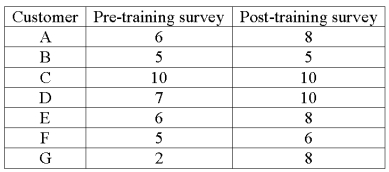What is the value of the test statistic?

A) 1.943
B) 1.895
C) 2.542
D) 2.447

Question 77

A company is researching the effectiveness of a new web site design to decrease the time to access a website. Five web site users were randomly selected and their times (in seconds) to access the web site with the old and new designs were recorded. The results follow. 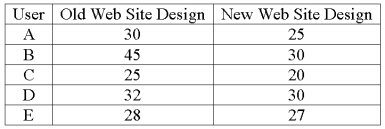What is the value of the test statistic?

A) 2.256
B) 1.895
C) 3.747
D) 2.447

Question 78

A company is researching the effectiveness of a new web site design to decrease the time to access a website. Five web site users were randomly selected and their times (in seconds) to access the web site with the old and new designs were recorded. The results follow.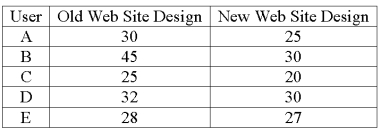
What is the alternative hypothesis?

A) H₁: µ_d = 0
B) H₁: µ_d $\neq$ 0
C) H₁: µ_d < 0
D) H₁: µ_d > 0

Question 79

Accounting procedures allow a business to evaluate their inventory at LIFO (Last In First Out) or FIFO (First In First Out). A manufacturer evaluated its finished goods inventory (in $ thousands) for five products both ways. Based on the following results, is LIFO more effective in keeping the value of his inventory lower?
If you use the 5% level of significance, what is the critical t value?

A) +2.132
B) $\pm$ 2.776
C) +2.262
D) $\pm$ 102.228

Question 80

Accounting procedures allow a business to evaluate their inventory at LIFO (Last In First Out) or FIFO (First In First Out). A manufacturer evaluated its finished goods inventory (in $ thousands) for five products both ways. Based on the following results, is LIFO more effective in keeping the value of his inventory lower? What are the degrees of freedom?

A) 4
B) 5
C) 15
D) 10