Deck 6: Discrete Probability Distributions
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/128
Play
Full screen (f)
Deck 6: Discrete Probability Distributions
1
Sixty percent of the customers of a fast food chain order a hamburger, french fries and a drink. If a random sample of 15 cash register receipts is selected, what is the probability that 10 or more will show that the above three food items were ordered?
A) 1.000
B) 0.186
C) 0.403
D) 0.000
A) 1.000
B) 0.186
C) 0.403
D) 0.000
C
2
To construct a binomial probability distribution, the mean must be known.
False
3
On a very hot summer day, 5 percent of the production employees at Midland States Steel are absent from work. The production employees are randomly selected for a special in-depth study on absenteeism. What is the probability of randomly selecting 10 production employees on a hot summer day and finding that none of them are absent?
A) 0.002
B) 0.344
C) 0.599
D) 0.100
A) 0.002
B) 0.344
C) 0.599
D) 0.100
C
4
The probabilities and the number of automobiles lined up at a Lakeside Olds at opening time (7:30 a.m.) for service are 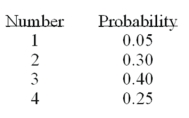 On a typical day, how many automobiles should Lakeside Olds expect to be lined up at opening?
On a typical day, how many automobiles should Lakeside Olds expect to be lined up at opening?
A) 10.00
B) 1.00
C) 2.85
D) 1.96
 On a typical day, how many automobiles should Lakeside Olds expect to be lined up at opening?
On a typical day, how many automobiles should Lakeside Olds expect to be lined up at opening?A) 10.00
B) 1.00
C) 2.85
D) 1.96

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
5
The variance of a probability distribution is based on the sum of squared differences from the mean.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
6
The binomial probability distribution is always negatively skewed.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
7
A random variable represents the outcomes of an experiment.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
8
The variance shows the skewness of a probability distribution.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
9
To construct a binomial distribution, it is necessary to know the total number of trials and the probability of success on each trial.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
10
As a general rule of thumb, if the items selected for a sample are not replaced and the sample size is less than 5 percent of the population, the binomial distribution can be used to approximate the hypergeometric distribution.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
11
A probability distribution is a mutually exclusive and collectively exhaustive listing of experimental outcomes that can occur by chance and their corresponding probabilities.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
12
Judging from recent experience, 5 percent of the computer keyboards produced by an automatic, high-speed machine are defective. If six keyboards are randomly selected, what is the probability that none of the keyboards are defective?
A) 0.001
B) 0.167
C) 0.735
D) 0.500
A) 0.001
B) 0.167
C) 0.735
D) 0.500

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
13
The mean of a probability distribution is called its expected value.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
14
The probability of a particular outcome must always be between 0 and 100 inclusive.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
15
The variance of a binomial distribution is found by n (1 - ).

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
16
In a Poisson distribution, the probability of success may vary from trial to trial.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
17
If the variance is 3.6 grams, what is the standard deviation?
A) 0.6
B) 1.897
C) 6.0
D) 12.96
A) 0.6
B) 1.897
C) 6.0
D) 12.96

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
18
The random variable for a Poisson probability distribution can assume an infinite number of values.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
19
When sampling is done without replacement and the outcomes are measured as either a success or failure, the hypergeometric distribution should be applied.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
20
The mean of a binomial distribution is the product of n and .

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
21
Which of the following is correct about a probability distribution?
A) Sum of all possible outcomes must equal 1
B) Outcomes must be mutually exclusive
C) Probability of each outcome must be between 0 and 1 inclusive
D) All of the above
A) Sum of all possible outcomes must equal 1
B) Outcomes must be mutually exclusive
C) Probability of each outcome must be between 0 and 1 inclusive
D) All of the above

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
22
A farmer who grows genetically engineered corn is experiencing trouble with corn borers. A random check of 5,000 ears revealed the following: many of the ears contained no borers. Some ears had one borer; a few had two borers; and so on. The distribution of the number of borers per ear approximated the Poisson distribution. The farmer counted 3,500 borers in the 5,000 ears. What is the probability that an ear of corn selected at random will contain no borers?
A) 0.3476
B) 0.4966
C) 1.000
D) 0.0631
A) 0.3476
B) 0.4966
C) 1.000
D) 0.0631

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
23
Chances are 50-50 that a newborn baby will be a girl. For families with five children, what is the probability that all the children are girls?
A) 0.900
B) 0.031
C) 0.001
D) 0.250
A) 0.900
B) 0.031
C) 0.001
D) 0.250

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
24
A true-false test consists of six questions. If you guess the answer to each question, what is the probability of getting all six questions correct?
A) 0
B) 0.016
C) 0.062
D) 0.250
A) 0
B) 0.016
C) 0.062
D) 0.250

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
25
Which is true for a binomial distribution?
A) There are three or more possible outcomes.
B) Probability of success remains the same from trial to trial.
C) Value of p is equal to 1.50.
D) It approximates the Poisson distribution.
A) There are three or more possible outcomes.
B) Probability of success remains the same from trial to trial.
C) Value of p is equal to 1.50.
D) It approximates the Poisson distribution.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
26
An insurance agent has appointments with four prospective clients tomorrow. From past experience the agent knows that the probability of making a sale on any appointment is 1 out of 5. Using the rules of probability, what is the likelihood that the agent will sell a policy to 3 of the 4 prospective clients?
A) 0.250
B) 0.500
C) 0.410
D) 0.026
A) 0.250
B) 0.500
C) 0.410
D) 0.026

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
27
The production department has installed a new spray machine to paint automobile doors. As is common with most spray guns, unsightly blemishes often appear because of improper mixture or other problems. A worker counted the number of blemishes on each door. Most doors had no blemishes; a few had one; a very few had two, and so on. The average number was 0.5 per door. The distribution of blemishes followed the Poisson distribution. Out of 10,000 doors painted, about how many would have no blemishes?
A) About 6,065
B) About 3,935
C) About 5,000
D) About 500
A) About 6,065
B) About 3,935
C) About 5,000
D) About 500

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
28
A tennis match requires that a player win three of five sets to win the match. If a player wins the first two sets, what is the probability that the player wins the match, assuming that each player is equally likely to win each match?
A) 0.5
B) ⅛ or 0.125
C) ⅞ or 0.875
D) Cannot be computed.
A) 0.5
B) ⅛ or 0.125
C) ⅞ or 0.875
D) Cannot be computed.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
29
A listing of all possible outcomes of an experiment and their corresponding probability of occurrence is called a ____________.
A) Random variable
B) Probability distribution
C) Subjective probability
D) Frequency distribution
A) Random variable
B) Probability distribution
C) Subjective probability
D) Frequency distribution

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
30
What kind of distribution are the binomial and Poisson distributions?
A) Discrete
B) Continuous
C) Both discrete and continuous
D) Neither discrete nor continuous
A) Discrete
B) Continuous
C) Both discrete and continuous
D) Neither discrete nor continuous

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
31
In a large metropolitan area, past records revealed that 30 percent of all the high school graduates go to college. From 20 graduates selected at random, what is the probability that exactly 8 will go to college?
A) 0.114
B) 0.887
C) 0.400
D) 0.231
A) 0.114
B) 0.887
C) 0.400
D) 0.231

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
32
A new car was put into production. It involved many assembly tasks. Each car was inspected at the end of the assembly line and the number of defects per unit was recorded. For the first 100 cars produced, there were 40 defective cars. Some of the cars had no defects; a few had one defect, and so on. The distribution of defects followed a Poisson distribution. Based on the first 100 produced, about how many out of every 1,000 cars assembled should have one or more defects?
A) About 660
B) About 165
C) About 630
D) About 330
A) About 660
B) About 165
C) About 630
D) About 330

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
33
The marketing department of a nationally known cereal maker plans to conduct a national survey to find out whether or not consumers of flake cereals can distinguish one of their favorite flake cereals. To test the questionnaire and procedure to be used, eight persons were asked to cooperate in an experiment. Five very small bowls of flake cereals were placed in front of a person. The bowls were labeled A, B, C, D and
A) 0.168
B) 0.009
C) 0.788
D) 0.125
E) The person was informed that only one bowl contained his or her favorite flake cereal. Suppose that the eight persons in the experiment were unable to identify their favorite cereal and just guessed which bowl it was in. What is the probability that none of the eight guessed correctly?
A) 0.168
B) 0.009
C) 0.788
D) 0.125
E) The person was informed that only one bowl contained his or her favorite flake cereal. Suppose that the eight persons in the experiment were unable to identify their favorite cereal and just guessed which bowl it was in. What is the probability that none of the eight guessed correctly?

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
34
Which one of the following is NOT a condition of the binomial distribution?
A) Independent trials
B) Only two outcomes
C) Probability of success remains constant from trial to trial
D) At least 10 observations
A) Independent trials
B) Only two outcomes
C) Probability of success remains constant from trial to trial
D) At least 10 observations

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
35
Data show that the weight of an offensive linesman may be any weight between 200 and 350 pounds. The distribution of weight is based on a
A) Continuous random variable
B) Discrete random variable
C) Qualitative variable
D) All of the above
A) Continuous random variable
B) Discrete random variable
C) Qualitative variable
D) All of the above

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
36
Sweetwater & Associates write weekend trip insurance at a very nominal charge. Records show that the probability that a motorist will have an accident during the weekend and file a claim is 0.0005. Suppose they wrote 400 policies for the coming weekend, what is the probability that exactly two claims will be filed?
A) 0.8187
B) 0.2500
C) 0.0164
D) 0.0001
A) 0.8187
B) 0.2500
C) 0.0164
D) 0.0001

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
37
A manufacturer of headache medicine claims it is 70 percent effective within a few minutes. That is, out of every 100 users 70 get relief within a few minutes. A group of 12 patients are given the medicine. If the claim is true, what is the probability that 8 have relief within a few minutes?
A) 0.001
B) 0.168
C) 0.667
D) 0.231
A) 0.001
B) 0.168
C) 0.667
D) 0.231

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
38
Sponsors of a local charity decided to attract wealthy patrons to its $500-a-plate dinner by allowing each patron to buy a set of 20 tickets for the gaming tables. The chance of winning a prize for each of the 20 plays is 50-50. If you bought 20 tickets, what is the chance of winning 15 or more prizes?
A) 0.250
B) 0.021
C) 0.006
D) 0.750
A) 0.250
B) 0.021
C) 0.006
D) 0.750

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
39
Carlson Jewelers permits the return of their diamond wedding rings, provided the return occurs within two weeks of the purchase date. Their records reveal that 10 percent of the diamond wedding rings are returned. Five different customers buy five rings. What is the probability that none will be returned?
A) 0.250
B) 0.073
C) 0.590
D) 0.500
E) 0.372
A) 0.250
B) 0.073
C) 0.590
D) 0.500
E) 0.372

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
40
Which shape describes a Poisson distribution?
A) Positively skewed
B) Negatively skewed
C) Symmetrical
D) All of the above
A) Positively skewed
B) Negatively skewed
C) Symmetrical
D) All of the above

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
41
A statistics professor receives an average of five e-mail messages per day from students. Assume the number of messages approximates a Poisson distribution. What is the probability that on a randomly selected day she will have two messages?
A) 0.0067
B) 0.0014
C) 0.420
D) 0.084
A) 0.0067
B) 0.0014
C) 0.420
D) 0.084

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
42
Which of the following is a requirement for use of the hypergeometric distribution?
A) Only 2 possible outcomes
B) Trials are independent
C) Probability of a success is greater than 1.0
D) Sampling with replacement
A) Only 2 possible outcomes
B) Trials are independent
C) Probability of a success is greater than 1.0
D) Sampling with replacement

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
43
In a Poisson distribution the variance is equal to
A) n
B)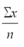
C) e-x
D)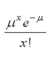
A) n
B)
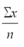
C) e-x
D)
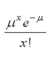

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
44
What must you know to develop a binomial probability distribution?
A) Probability of success
B) Probability of success and the number of trials
C) Probability of success and the number of successes
D) Number of trials and the number of successes
A) Probability of success
B) Probability of success and the number of trials
C) Probability of success and the number of successes
D) Number of trials and the number of successes

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
45
A statistics professor receives an average of five e-mail messages per day from students. Assume the number of messages approximates a Poisson distribution. What is the probability that on a randomly selected day she will have no messages?
A) 0.0067
B) Zero
C) 0.0335
D) Impossible to have no messages
A) 0.0067
B) Zero
C) 0.0335
D) Impossible to have no messages

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
46
A company is studying the number of monthly absences among its 125 employees. The following probability distribution shows the likelihood that people were absent 0, 1, 2, 3, 4, or 5 days last month.  What is the mode of the distribution?
What is the mode of the distribution?
A) 0.72 days
B) 2.5 days
C) 0 days
D) 3 days
 What is the mode of the distribution?
What is the mode of the distribution?A) 0.72 days
B) 2.5 days
C) 0 days
D) 3 days

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
47
In which of the following discrete distribution does the probability of a success vary from one trial to the next?
A) Binomial
B) Poisson
C) Hypergeometric
D) All of the above
A) Binomial
B) Poisson
C) Hypergeometric
D) All of the above

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
48
A company is studying the number of monthly absences among its 125 employees. The following probability distribution shows the likelihood that people were absent 0, 1, 2, 3, 4, or 5 days last month.  What is the variance of the number of days absent?
What is the variance of the number of days absent?
A) 1.62
B) 1.41
C) 5.00
D) 55.52
 What is the variance of the number of days absent?
What is the variance of the number of days absent?A) 1.62
B) 1.41
C) 5.00
D) 55.52

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
49
A company is studying the number of monthly absences among its 125 employees. The following probability distribution shows the likelihood that people were absent 0, 1, 2, 3, 4, or 5 days last month.  What is the mean number of days absent?
What is the mean number of days absent?
A) 1.00
B) 0.40
C) 0.72
D) 2.5
 What is the mean number of days absent?
What is the mean number of days absent?A) 1.00
B) 0.40
C) 0.72
D) 2.5

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
50
A company is studying the number of monthly absences among its 125 employees. The following probability distribution shows the likelihood that people were absent 0, 1, 2, 3, 4, or 5 days last month.  Given the probability distribution, which of the following predictions is correct?
Given the probability distribution, which of the following predictions is correct?
A) 60% of the employees will have more than one day absent for a month.
B) There is a 0.04 probability that an employee will be absent 1 day during a month.
C) There is a 0.12 probability that an employee will be absent 2 days during a month.
D) There is a 0.50 probability that an employee will be absent 0.72 days during a month.
 Given the probability distribution, which of the following predictions is correct?
Given the probability distribution, which of the following predictions is correct?A) 60% of the employees will have more than one day absent for a month.
B) There is a 0.04 probability that an employee will be absent 1 day during a month.
C) There is a 0.12 probability that an employee will be absent 2 days during a month.
D) There is a 0.50 probability that an employee will be absent 0.72 days during a month.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
51
A machine shop has 100 drill presses and other machines in constant use. The probability that a machine will become inoperative during a given day is 0.002. During some days no machines are inoperative, but during some days, one, two, three or more are broken down. What is the probability that fewer than two machines will be inoperative during a particular day?
A) 0.0200
B) 0.1637
C) 0.8187
D) 0.9824
A) 0.0200
B) 0.1637
C) 0.8187
D) 0.9824

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
52
Which of the following is NOT a characteristic of a binomial probability distribution?
A) Each outcome is mutually exclusive
B) Each trial is independent
C) Probability of success remains constant from trial to trial
D) Each outcome results from two trials
A) Each outcome is mutually exclusive
B) Each trial is independent
C) Probability of success remains constant from trial to trial
D) Each outcome results from two trials

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
53
What is the following table called? 
A) Probability distribution
B) Cumulative frequency distribution
C) Standard deviation
D) Frequency table

A) Probability distribution
B) Cumulative frequency distribution
C) Standard deviation
D) Frequency table

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
54
What is the only variable in the Poisson probability formula?
A)
B) x
C) e
D) P
A)
B) x
C) e
D) P

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
55
In a Poisson distribution the mean is equal to
A) n
B)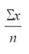
C) e-x
D)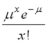
A) n
B)
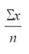
C) e-x
D)
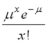

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
56
David's gasoline station offers 4 cents off per gallon if the customer pays in cash and does not use a credit card. Past evidence indicates that 40% of all customers pay in cash. During a one-hour period twenty-five customers buy gasoline at this station. This situation is an example of what type of discrete probability distribution?
A) Continuous probability distribution
B) Poisson probability distribution
C) Binomial probability distribution
D) Hypergeometric probability distribution
A) Continuous probability distribution
B) Poisson probability distribution
C) Binomial probability distribution
D) Hypergeometric probability distribution

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
57
David's gasoline station offers 4 cents off per gallon if the customer pays in cash and does not use a credit card. Past evidence indicates that 40% of all customers pay in cash. During a one-hour period twenty-five customers buy gasoline at this station. What is the probability that no more than twenty pay in cash?
A) 0.0
B) 0.1
C) 0.9
D) 1.0
A) 0.0
B) 0.1
C) 0.9
D) 1.0

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
58
David's gasoline station offers 4 cents off per gallon if the customer pays in cash and does not use a credit card. Past evidence indicates that 40% of all customers pay in cash. During a one-hour period twenty-five customers buy gasoline at this station. What is the probability that more than ten and less than fifteen customers pay in cash?
A) 0.541
B) 0.401
C) 0.380
D) 0.562
A) 0.541
B) 0.401
C) 0.380
D) 0.562

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
59
David's gasoline station offers 4 cents off per gallon if the customer pays in cash and does not use a credit card. Past evidence indicates that 40% of all customers pay in cash. During a one-hour period twenty-five customers buy gasoline at this station. What is the probability that at least ten pay in cash?
A) 0.416
B) 0.575
C) 0.586
D) 0.425
A) 0.416
B) 0.575
C) 0.586
D) 0.425

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
60
A statistics professor receives an average of five e-mail messages per day from students. Assume the number of messages approximates a Poisson distribution. What is the probability that on a randomly selected day she will have five messages?
A) 0.0067
B) 0.875
C) 0.175
D) 1.0
A) 0.0067
B) 0.875
C) 0.175
D) 1.0

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
61
The following is a binomial probability distribution with n = 3 and = 0.20. 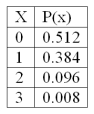
The variance of the distribution is
A) 1.5
B) 3.0
C) 0.69
D) 0.48

The variance of the distribution is
A) 1.5
B) 3.0
C) 0.69
D) 0.48

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
62
To construct a binomial distribution we need to know the ___________ and the probability of a success.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
63
The following is a Poisson probability distribution with µ = 0.1. 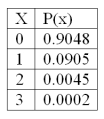 The variance of the distribution is
The variance of the distribution is
A) 1.0
B) 0.9046
C) 3.0
D) 0.1
 The variance of the distribution is
The variance of the distribution isA) 1.0
B) 0.9046
C) 3.0
D) 0.1

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
64
A probability distribution is a listing of the expected outcomes of an experiment and the probability of each outcome occurring. What is the sum of the probabilities? _____

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
65
For a binomial distribution, the mean is 4.0 and n = 8. What is for this distribution?
A) 0.5
B) 1.00
C) 4.0
D) 0.1
A) 0.5
B) 1.00
C) 4.0
D) 0.1

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
66
The following is a binomial probability distribution with n = 3 and = 0.20. 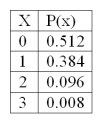
The mean of the distribution is
A) 1.5
B) 0.6
C) 0.25
D) 0.0

The mean of the distribution is
A) 1.5
B) 0.6
C) 0.25
D) 0.0

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
67
Affirmative action commitments by many organizations have led to an increase in the number of women in executive positions. Satellite Office Systems has vacancies for two executives that it will fill from among four women and six men. What is the probability that no woman is selected?
A) 1/5
B) 1/3
C) 2/15
D) 8/15
A) 1/5
B) 1/3
C) 2/15
D) 8/15

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
68
For a binomial distribution, the mean is 0.6 and n = 2. What is for this distribution?
A) 0.5
B) 1.00
C) 0.3
D) 0.1
A) 0.5
B) 1.00
C) 0.3
D) 0.1

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
69
For the following distribution, 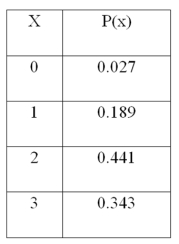 What is the variance of the distribution?
What is the variance of the distribution?
A) 2.1
B) 0.63
C) 3.9
D) 2.754
 What is the variance of the distribution?
What is the variance of the distribution?A) 2.1
B) 0.63
C) 3.9
D) 2.754

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
70
Affirmative action commitments by many organizations have led to an increase in the number of women in executive positions. Satellite Office Systems has vacancies for two executives that it will fill from among four women and six men. What is the probability that at least one woman is selected?
A) 8/15
B) 3/5
C) 2/3
D) 3/4
A) 8/15
B) 3/5
C) 2/3
D) 3/4

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
71
A company is studying the number of monthly absences among its 125 employees. The following probability distribution shows the likelihood that people were absent 0, 1, 2, 3, 4, or 5 days last month.  What is the standard deviation of the number of days absent?
What is the standard deviation of the number of days absent?
A) 1.1616
B) 0
C) 1.6595
D) 1.0778
 What is the standard deviation of the number of days absent?
What is the standard deviation of the number of days absent?A) 1.1616
B) 0
C) 1.6595
D) 1.0778

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
72
For the following distribution, 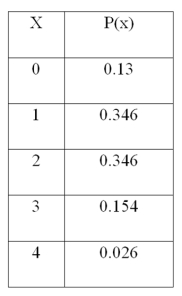 What is the variance of the distribution?
What is the variance of the distribution?
A) 1.1616
B) 0.964
C) 0.982
D) 1.000
 What is the variance of the distribution?
What is the variance of the distribution?A) 1.1616
B) 0.964
C) 0.982
D) 1.000

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
73
Affirmative action commitments by many organizations have led to an increase in the number of women in executive positions. Satellite Office Systems has vacancies for two executives that it will fill from among four women and six men.
What probability distribution should be applied? ___________
What probability distribution should be applied? ___________

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
74
How many experimental outcomes are possible for the Binomial distribution? _______

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
75
For the following distribution, 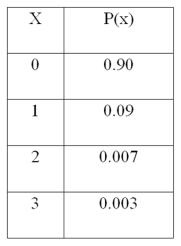 What is the mean of the distribution?
What is the mean of the distribution?
A) 2.1
B) 1.13
C) 0.113
D) 1.5
 What is the mean of the distribution?
What is the mean of the distribution?A) 2.1
B) 1.13
C) 0.113
D) 1.5

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
76
For the following distribution, 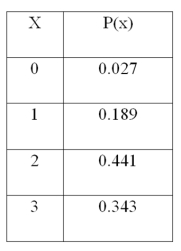 What is the mean of the distribution?
What is the mean of the distribution?
A) 2.1
B) 1.5
C) 0.441
D) 2
 What is the mean of the distribution?
What is the mean of the distribution?A) 2.1
B) 1.5
C) 0.441
D) 2

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
77
The following is a Poisson probability distribution with µ = 0.1. 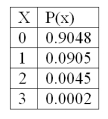 The mean of the distribution is
The mean of the distribution is
A) 1.5
B) 0.1
C) 0.25
D) 1.0
 The mean of the distribution is
The mean of the distribution isA) 1.5
B) 0.1
C) 0.25
D) 1.0

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
78
A probability distribution shows the outcomes of an experiment and the ___________________ of each one occurring.

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
79
For the following distribution, 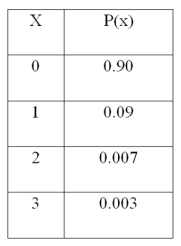 What is the variance of the distribution?
What is the variance of the distribution?
A) 2.1
B) 0.132
C) 0.364
D) 1.000
 What is the variance of the distribution?
What is the variance of the distribution?A) 2.1
B) 0.132
C) 0.364
D) 1.000

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck
80
For the following distribution, 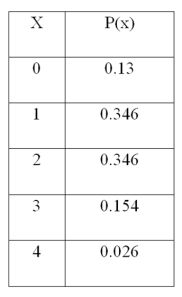 What is the mean of the distribution?
What is the mean of the distribution?
A) 1
B) 2.5
C) 1.604
D) 3
 What is the mean of the distribution?
What is the mean of the distribution?A) 1
B) 2.5
C) 1.604
D) 3

Unlock Deck
Unlock for access to all 128 flashcards in this deck.
Unlock Deck
k this deck


