Deck 8: Extension: The Transportation Model
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/20
Play
Full screen (f)
Deck 8: Extension: The Transportation Model
1
The transportation method is a linear programming technique. Linearity is present in the following way:
A) The cost of goods shipped from any source to any destination is a linear function of quantity shipped.
B) The cost of goods shipped from any source to any destination is a linear function of the cost per unit.
C) The total cost associated with a given plan is a linear function of shipping costs.
D) Cell evaluations require linear horizontal movements through the matrix.
E) Cell evaluations are linear.
A) The cost of goods shipped from any source to any destination is a linear function of quantity shipped.
B) The cost of goods shipped from any source to any destination is a linear function of the cost per unit.
C) The total cost associated with a given plan is a linear function of shipping costs.
D) Cell evaluations require linear horizontal movements through the matrix.
E) Cell evaluations are linear.
The cost of goods shipped from any source to any destination is a linear function of quantity shipped.
2
A transportation planner has set up the following spreadsheet formulation of a transportation problem: 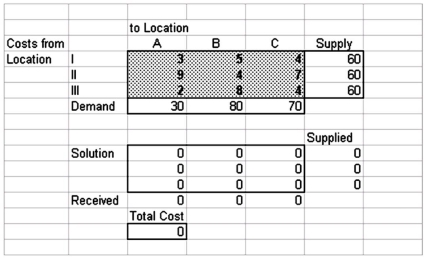 Suppose the output from this formulation is as follows:
Suppose the output from this formulation is as follows:
How many units are shipped from location II to location C?
A) 0
B) 60
C) 70
D) 80
E) none of these
 Suppose the output from this formulation is as follows:
Suppose the output from this formulation is as follows: How many units are shipped from location II to location C?
A) 0
B) 60
C) 70
D) 80
E) none of these
0
3
In a transportation problem with three locations and two destinations, the objective function is as follows: Min 20X11 + 18X21 + 23X31 + 16X12 + 14X22 + 12X32. How much does it cost to ship one unit from location 1 to destination 2?
A) 18
B) 12
C) 23
D) 16
E) 14
A) 18
B) 12
C) 23
D) 16
E) 14
16
4
Suppose a decision maker is confronted with the following transportation model scenario: 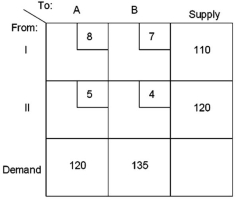 In the optimal solution, destination A receives how many units?
In the optimal solution, destination A receives how many units?
A) 0
B) 35
C) 70
D) 95
E) 120
 In the optimal solution, destination A receives how many units?
In the optimal solution, destination A receives how many units?A) 0
B) 35
C) 70
D) 95
E) 120

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
5
Suppose a decision maker is confronted with the following transportation model scenario: 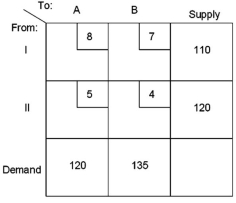 What is the total cost of the optimal solution?
What is the total cost of the optimal solution?
A) $1,300
B) $1,345
C) $1,354
D) $1,410
E) $1,455
 What is the total cost of the optimal solution?
What is the total cost of the optimal solution?A) $1,300
B) $1,345
C) $1,354
D) $1,410
E) $1,455

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
6
Which of the following is the information needed to use the transportation model?
(I) A list of the sources and each one's capacity
(II) A list of the destinations and each one's demand
(III) The unit cost of shipping items from each source to each destination
A) I and II only
B) II and III only
C) I and III only
D) III only
E) I, II, and III
(I) A list of the sources and each one's capacity
(II) A list of the destinations and each one's demand
(III) The unit cost of shipping items from each source to each destination
A) I and II only
B) II and III only
C) I and III only
D) III only
E) I, II, and III

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
7
A campaign manager for a political candidate must arrange the shipment of 150 cartons of campaign buttons from three button producers to three campaign headquarters. The supplies and demands, and the per-carton transportation costs, are shown below: 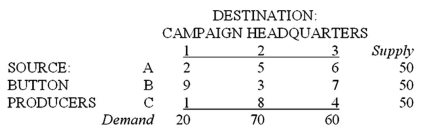 Which of the following is a constraint for the suppliers (button producers)?
Which of the following is a constraint for the suppliers (button producers)?
A)
B)
C)
D)
E) all of the choices
 Which of the following is a constraint for the suppliers (button producers)?
Which of the following is a constraint for the suppliers (button producers)?A)
B)
C)
D)
E) all of the choices

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
8
Suppose a decision maker is confronted with the following transportation model scenario: 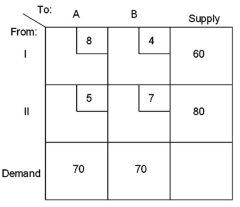 What is the total cost of the optimal solution?
What is the total cost of the optimal solution?
A) $600
B) $620
C) $640
D) $660
E) $680
 What is the total cost of the optimal solution?
What is the total cost of the optimal solution?A) $600
B) $620
C) $640
D) $660
E) $680

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
9
The transportation model method for evaluating location alternatives minimizes total:
A) sources.
B) destinations.
C) capacity.
D) demand.
E) shipping cost.
A) sources.
B) destinations.
C) capacity.
D) demand.
E) shipping cost.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
10
The transportation model assumes similar, homogeneous goods.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
11
Suppose a decision maker is confronted with the following transportation model scenario: 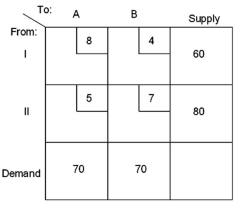 In the optimal solution, how many units are shipped from source II to destination B?
In the optimal solution, how many units are shipped from source II to destination B?
A) 0
B) 10
C) 60
D) 70
E) 80
 In the optimal solution, how many units are shipped from source II to destination B?
In the optimal solution, how many units are shipped from source II to destination B?A) 0
B) 10
C) 60
D) 70
E) 80

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
12
The transportation model assumes shipping cost per unit is the same regardless of the number of units shipped (there are no quantity discounts).

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
13
An automobile manufacturer that has eight assembly plants and thousands of dealers throughout the United States can find the optimal distribution plan by using:
(I) a linear programming model.
(II) the transportation model.
(III) weighted factor ratings.
(IV) global information systems.
A) I only
B) II only
C) II or III
D) I or II
E) I or IV
(I) a linear programming model.
(II) the transportation model.
(III) weighted factor ratings.
(IV) global information systems.
A) I only
B) II only
C) II or III
D) I or II
E) I or IV

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
14
Which of the following is not an assumption of the transportation model?
A) Actual supply and demand must be equal.
B) Shipping costs per unit are constant per unit.
C) Items to be shipped are homogeneous.
D) There is only one transportation route between each source and destination.
E) There is only one transportation mode between each source and destination.
A) Actual supply and demand must be equal.
B) Shipping costs per unit are constant per unit.
C) Items to be shipped are homogeneous.
D) There is only one transportation route between each source and destination.
E) There is only one transportation mode between each source and destination.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
15
Which of the following are assumptions or requirements of the transportation method?
(I) Goods are the same, regardless of source.
(II) There must be multiple sources.
(III) Minimum quantities must be shipped from each source.
(IV) Shipping costs per unit do not vary with the quantity shipped.
A) I and IV
B) II and III
C) I, II, and IV
D) I and III
E) I, II, III, and IV
(I) Goods are the same, regardless of source.
(II) There must be multiple sources.
(III) Minimum quantities must be shipped from each source.
(IV) Shipping costs per unit do not vary with the quantity shipped.
A) I and IV
B) II and III
C) I, II, and IV
D) I and III
E) I, II, III, and IV

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
16
A campaign manager for a political candidate must arrange the shipment of 150 cartons of campaign buttons from three button producers to three campaign headquarters. The supplies and demands, and the per-carton transportation costs, are shown below: 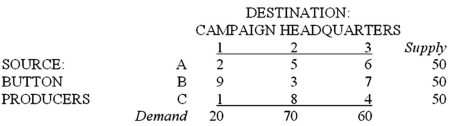 Which of the following is a constraint for the customer (campaign headquarters)?
Which of the following is a constraint for the customer (campaign headquarters)?
A) 2X11 + 9X21 + X31 = 20
B) 5X12 + 3X22 + 8X32 = 70
C) X11 + X12 + X13 = 50
D) X12 + X22 + X32 = 70
E) all of the choices
 Which of the following is a constraint for the customer (campaign headquarters)?
Which of the following is a constraint for the customer (campaign headquarters)?A) 2X11 + 9X21 + X31 = 20
B) 5X12 + 3X22 + 8X32 = 70
C) X11 + X12 + X13 = 50
D) X12 + X22 + X32 = 70
E) all of the choices

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
17
A transportation planner has set up the following spreadsheet formulation of a transportation problem: 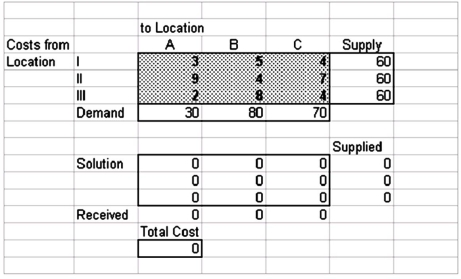 This model indicates that it costs ________ dollars to ship one unit from location(s) _______ to location(s) ___.
This model indicates that it costs ________ dollars to ship one unit from location(s) _______ to location(s) ___.
A) 60; I; A, B, & C
B) 30; I, II, & III; A
C) 5; II; B
D) 9; II; A
E) 7; III; C
 This model indicates that it costs ________ dollars to ship one unit from location(s) _______ to location(s) ___.
This model indicates that it costs ________ dollars to ship one unit from location(s) _______ to location(s) ___.A) 60; I; A, B, & C
B) 30; I, II, & III; A
C) 5; II; B
D) 9; II; A
E) 7; III; C

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
18
A campaign manager for a political candidate must arrange the shipment of 150 cartons of campaign buttons from three button producers to three campaign headquarters. The supplies and demands, and the per-carton transportation costs, are shown below: 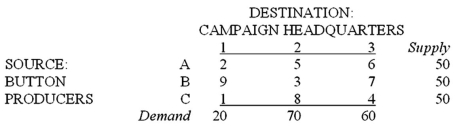 Which of the following is an objective function for the problem?
Which of the following is an objective function for the problem?
A)
B)
C)
D)
E) None of the choices.
 Which of the following is an objective function for the problem?
Which of the following is an objective function for the problem?A)
B)
C)
D)
E) None of the choices.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
19
Which of the following is not information needed to use the transportation model?
A) capacity of the sources
B) demand of the destinations
C) unit shipping costs
D) unit shipping distances
E) All of the choices are necessary.
A) capacity of the sources
B) demand of the destinations
C) unit shipping costs
D) unit shipping distances
E) All of the choices are necessary.

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck
20
In a transportation problem with three locations and two destinations, the objective function is as follows: Min 20X11 + 18X21 + 23X31 + 16X12 + 14X22 + 12X32. How much does it cost to ship one unit from location 2 to destination 1?
A) 18
B) 12
C) 23
D) 16
E) none of the choices
A) 18
B) 12
C) 23
D) 16
E) none of the choices

Unlock Deck
Unlock for access to all 20 flashcards in this deck.
Unlock Deck
k this deck


