Deck 17: Multiple Regression
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/160
Play
Full screen (f)
Deck 17: Multiple Regression
1
In multiple regression,the standard error of estimate is defined by 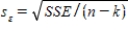 ,where n is the sample size and k is the number of independent variables.
,where n is the sample size and k is the number of independent variables.
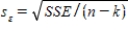 ,where n is the sample size and k is the number of independent variables.
,where n is the sample size and k is the number of independent variables.False
2
When an additional explanatory variable is introduced into a multiple regression model,the coefficient of determination will never decrease.
True
3
In order to test the significance of a multiple regression model involving 4 independent variables and 25 observations,the numerator and denominator degrees of freedom for the critical value of F are 3 and 21,respectively.
False
4
In multiple regression analysis,the adjusted coefficient of determination is adjusted for the number of independent variables and the sample size.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
5
A multiple regression is called "multiple" because it has several explanatory variables.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
6
In reference to the equation 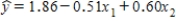 ,the value 0.60 is the average change in y per unit change in x2,regardless of the value of x1.
,the value 0.60 is the average change in y per unit change in x2,regardless of the value of x1.
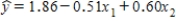 ,the value 0.60 is the average change in y per unit change in x2,regardless of the value of x1.
,the value 0.60 is the average change in y per unit change in x2,regardless of the value of x1.
Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
7
In reference to the equation 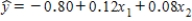 ,the value −0.80 is the y-intercept.
,the value −0.80 is the y-intercept.
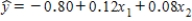 ,the value −0.80 is the y-intercept.
,the value −0.80 is the y-intercept.
Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
8
A multiple regression model involves 40 observations and 4 independent variables produces a total variation in y of 100,000 and SSR = 80,400.Then,the value of MSE is 560.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
9
In reference to the equation 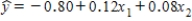 ,the value 0.12 is the average change in y per unit change in x1,when x2 is held constant.
,the value 0.12 is the average change in y per unit change in x1,when x2 is held constant.
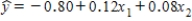 ,the value 0.12 is the average change in y per unit change in x1,when x2 is held constant.
,the value 0.12 is the average change in y per unit change in x1,when x2 is held constant.
Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
10
In regression analysis,the total variation in the dependent variable y,measured by 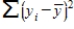 ,can be decomposed into two parts: the explained variation,measured by SSR,and the unexplained variation,measured by SSE.
,can be decomposed into two parts: the explained variation,measured by SSR,and the unexplained variation,measured by SSE.
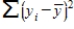 ,can be decomposed into two parts: the explained variation,measured by SSR,and the unexplained variation,measured by SSE.
,can be decomposed into two parts: the explained variation,measured by SSR,and the unexplained variation,measured by SSE.
Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
11
When an additional explanatory variable is introduced into a multiple regression model,coefficient of determination adjusted for degrees of freedom can never decrease.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
12
In a multiple regression analysis involving 4 independent variables and 30 data points,the number of degrees of freedom associated with the sum of squares for error,SSE,is 25.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
13
In testing the significance of a multiple regression model with three independent variables,the null hypothesis is 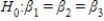 .
.
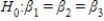 .
.
Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
14
In a multiple regression analysis involving 50 observations and 5 independent variables,the total variation in y is 475 and SSE = 71.25.Then,the coefficient of determination is 0.85.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
15
A multiple regression equation has a coefficient of determination of 0.81.Then,the percentage of the variation in y that is explained by the regression equation is 90%.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
16
In multiple regression analysis,when the response surface (the graphical depiction of the regression equation)hits every single point,the sum of squares for error SSE = 0,the standard error of estimate sε = 0,and the coefficient of determination R2 = 1.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
17
Most statistical software print a second R2 statistic,called the coefficient of determination adjusted for degrees of freedom,which has been adjusted to take into account the sample size and the number of independent variables.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
18
A multiple regression model is assessed to be good if the error sum of squares SSE and the standard error of estimate sε are both small,the coefficient of determination R2 is close to 1,and the value of the test statistic F is large.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
19
A small value of F indicates that most of the variation in y is explained by the regression equation and that the model is useful.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
20
The coefficient of determination R2 measures the proportion of variation in y that is explained by the explanatory variables included in the model.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
21
In multiple regression analysis,the ratio MSR/MSE yields the:
A)t-test statistic for testing each individual regression coefficient.
B)F-test statistic for testing the validity of the regression equation.
C)coefficient of determination.
D)adjusted coefficient of determination.
A)t-test statistic for testing each individual regression coefficient.
B)F-test statistic for testing the validity of the regression equation.
C)coefficient of determination.
D)adjusted coefficient of determination.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
22
The adjusted coefficient of determination is adjusted for the:
A)number of independent variables and the sample size.
B)number of dependent variables and the sample size.
C)coefficient of correlation and the significance level.
D)number of regression parameters including the y-intercept.
A)number of independent variables and the sample size.
B)number of dependent variables and the sample size.
C)coefficient of correlation and the significance level.
D)number of regression parameters including the y-intercept.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
23
The total variation in y in a regression model will never exceed the regression sum of squares (SSR).

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
24
When an explanatory variable is dropped from a multiple regression model,the adjusted coefficient of determination can increase.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
25
A multiple regression model is assessed to be poor if the error sum of squares SSE and the standard error of estimate sε are both large,the coefficient of determination R2 is close to 0,and the value of the test statistic F is large.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
26
When an explanatory variable is dropped from a multiple regression model,the coefficient of determination can increase.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
27
In order to test the validity of a multiple regression model involving 5 independent variables and 30 observations,the numerator and denominator degrees of freedom for the critical value of F are,respectively,
A)5 and 30
B)6 and 29
C)5 and 24
D)6 and 25
A)5 and 30
B)6 and 29
C)5 and 24
D)6 and 25

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
28
A multiple regression model has the form 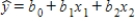 .The coefficient b1 is interpreted as the average change in y per unit change in x1.
.The coefficient b1 is interpreted as the average change in y per unit change in x1.
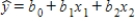 .The coefficient b1 is interpreted as the average change in y per unit change in x1.
.The coefficient b1 is interpreted as the average change in y per unit change in x1.
Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
29
In a multiple regression analysis involving 6 independent variables,the total variation in y is 900 and SSR = 600.What is the value of SSE?
A)300
B)1.50
C)0.67
D)None of these choices.
A)300
B)1.50
C)0.67
D)None of these choices.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
30
In a multiple regression analysis,if the model provides a poor fit,this indicates that:
A)the coefficient of determination will be close to zero.
B)the standard error of estimate will be large.
C)the sum of squares for error will be large.
D)All of these choices are true.
A)the coefficient of determination will be close to zero.
B)the standard error of estimate will be large.
C)the sum of squares for error will be large.
D)All of these choices are true.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
31
In calculating the standard error of the estimate, 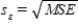 ,there are (n−k− 1)degrees of freedom,where n is the sample size and k is the number of independent variables in the model.
,there are (n−k− 1)degrees of freedom,where n is the sample size and k is the number of independent variables in the model.
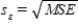 ,there are (n−k− 1)degrees of freedom,where n is the sample size and k is the number of independent variables in the model.
,there are (n−k− 1)degrees of freedom,where n is the sample size and k is the number of independent variables in the model.
Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
32
A multiple regression model has the form: 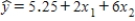 .As x2 increases by one unit,holding x1 constant,then the value of y will increase by:
.As x2 increases by one unit,holding x1 constant,then the value of y will increase by:
A)7.25 units
B)6 units on average
C)2 units
D)None of these choices
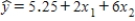 .As x2 increases by one unit,holding x1 constant,then the value of y will increase by:
.As x2 increases by one unit,holding x1 constant,then the value of y will increase by:A)7.25 units
B)6 units on average
C)2 units
D)None of these choices

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
33
A multiple regression model has the form 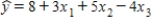 .As x3 increases by one unit,with x1 and x2 held constant,the y on average is expected to:
.As x3 increases by one unit,with x1 and x2 held constant,the y on average is expected to:
A)increase by 1 unit.
B)increase by 12 units.
C)decrease by 4 units.
D)decrease by 16 units.
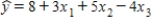 .As x3 increases by one unit,with x1 and x2 held constant,the y on average is expected to:
.As x3 increases by one unit,with x1 and x2 held constant,the y on average is expected to:A)increase by 1 unit.
B)increase by 12 units.
C)decrease by 4 units.
D)decrease by 16 units.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
34
A high value of the coefficient of determination significantly above 0 in multiple regression,accompanied by insignificant t-statistics on all parameter estimates,very often indicates a high correlation between independent variables in the model.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
35
Suppose a multiple regression analysis involving 25 data points has 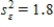 and SSE = 36.Then,the number of the independent variables must be:
and SSE = 36.Then,the number of the independent variables must be:
A)3
B)4
C)5
D)6
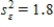 and SSE = 36.Then,the number of the independent variables must be:
and SSE = 36.Then,the number of the independent variables must be:A)3
B)4
C)5
D)6

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
36
A multiple regression model involves 5 independent variables and a sample of 10 data points.If we want to test the validity of the model at the 5% significance level,the critical value is:
A)6.26
B)3.33
C)9.36
D)4.24
A)6.26
B)3.33
C)9.36
D)4.24

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
37
From the coefficient of determination,we cannot detect the strength of the relationship between the dependent variable y and any individual independent variable.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
38
A multiple regression model involves 10 independent variables and 30 observations.If we want to test at the 5% significance level whether one of the coefficients is = 0 (vs.≠ 0)the critical value will be:
A)2.228
B)2.093
C)1.729
D)1.697
A)2.228
B)2.093
C)1.729
D)1.697

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
39
In a multiple regression model,the mean of the probability distribution of the error variable ε is assumed to be:
A)k,where k is the number of independent variables included in the model.
B)1.0
C)0.0
D)None of these choices.
A)k,where k is the number of independent variables included in the model.
B)1.0
C)0.0
D)None of these choices.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
40
In a multiple regression analysis involving k independent variables and n data points,the number of degrees of freedom associated with the sum of squares for error is:
A)k− 1
B)n−k
C)n− 1
D)n−k− 1
A)k− 1
B)n−k
C)n− 1
D)n−k− 1

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
41
In a multiple regression model,the value of the coefficient of determination has to fall between
A)−1 and +1.
B)0 and +1.
C)−1 and 0.
D)None of these choices.
A)−1 and +1.
B)0 and +1.
C)−1 and 0.
D)None of these choices.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
42
If all the points for a multiple regression model with two independent variables were right on the regression plane,then the coefficient of determination would equal:
A)0.
B)1.
C)2,since there are two independent variables.
D)None of these choices.
A)0.
B)1.
C)2,since there are two independent variables.
D)None of these choices.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
43
A multiple regression analysis involving three independent variables and 25 data points results in a value of 0.769 for the unadjusted coefficient of determination.Then,the adjusted coefficient of determination is:
A)0.385
B)0.877
C)0.591
D)0.736
A)0.385
B)0.877
C)0.591
D)0.736

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
44
For a multiple regression model,the following statistics are given: Total variation in y = 500,SSE = 80,and n = 25.Then,the coefficient of determination is:
A)0.84
B)0.16
C)0.3125
D)0.05
A)0.84
B)0.16
C)0.3125
D)0.05

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
45
To test the validity of a multiple regression model,we test the null hypothesis that the regression coefficients are all zero by applying the:
A)F-test
B)t-test
C)z-test
D)None of these choices.
A)F-test
B)t-test
C)z-test
D)None of these choices.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
46
In a multiple regression analysis involving 40 observations and 5 independent variables,the following statistics are given: Total variation in y = 350 and SSE = 50.Then,the coefficient of determination is:
A)0.8408
B)0.8571
C)0.8469
D)0.8529
A)0.8408
B)0.8571
C)0.8469
D)0.8529

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
47
For a multiple regression model the following statistics are given: Total variation in y = 250,SSE = 50,k = 4,and n = 20.Then,the coefficient of determination adjusted for the degrees of freedom is:
A)0.800
B)0.747
C)0.840
D)0.775
A)0.800
B)0.747
C)0.840
D)0.775

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
48
A multiple regression model has the form 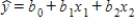 .The coefficient b1 is interpreted as the change in the average value of y per unit change in ________ holding ________ constant.
.The coefficient b1 is interpreted as the change in the average value of y per unit change in ________ holding ________ constant.
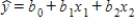 .The coefficient b1 is interpreted as the change in the average value of y per unit change in ________ holding ________ constant.
.The coefficient b1 is interpreted as the change in the average value of y per unit change in ________ holding ________ constant.
Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
49
In a multiple regression model,the following statistics are given: SSE = 100,R2 = 0.995,k = 5,and n = 15.Then,the coefficient of determination adjusted for degrees of freedom is:
A)0.992
B)0.900
C)0.955
D)0.855
A)0.992
B)0.900
C)0.955
D)0.855

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
50
In a multiple regression model,the error variable ε is assumed to have a mean of:
A)−1.0
B)0.0
C)1.0
D)None of these choices.
A)−1.0
B)0.0
C)1.0
D)None of these choices.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
51
For the multiple regression model: 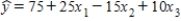 ,if x2 were to increase by 5,holding x1 and x3 constant,the value of y will:
,if x2 were to increase by 5,holding x1 and x3 constant,the value of y will:
A)increase by 5.
B)increase by 75.
C)decrease on average by 5.
D)decrease on average by 75.
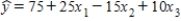 ,if x2 were to increase by 5,holding x1 and x3 constant,the value of y will:
,if x2 were to increase by 5,holding x1 and x3 constant,the value of y will:A)increase by 5.
B)increase by 75.
C)decrease on average by 5.
D)decrease on average by 75.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
52
Multiple regression has four requirements for the error variable.One is that the probability distribution of the error variable is ____________________.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
53
A multiple regression equation includes 5 independent variables,and the coefficient of determination is 0.81.The percentage of the variation in y that is explained by the regression equation is:
A)81%
B)90%
C)86%
D)about 16%
A)81%
B)90%
C)86%
D)about 16%

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
54
The coefficient of determination ranges from:
A)1.0 to ∞.
B)0.0 to 1.0.
C)1.0 to k,where k is the number of independent variables in the model.
D)1.0 to n,where n is the number of observations in the dependent variable.
A)1.0 to ∞.
B)0.0 to 1.0.
C)1.0 to k,where k is the number of independent variables in the model.
D)1.0 to n,where n is the number of observations in the dependent variable.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
55
A multiple regression model has:
A)only one independent variable.
B)only two independent variables.
C)more than one dependent variable.
D)more than one independent variable.
A)only one independent variable.
B)only two independent variables.
C)more than one dependent variable.
D)more than one independent variable.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
56
For the following multiple regression model: 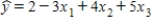 ,a unit increase in x1,holding x2 and x3 constant,results in:
,a unit increase in x1,holding x2 and x3 constant,results in:
A)a decrease of 3 units on average in the value of y.
B)an increase of 8 units in the value of y.
C)an increase of 3 units on average in the value of y.
D)None of these choices.
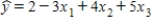 ,a unit increase in x1,holding x2 and x3 constant,results in:
,a unit increase in x1,holding x2 and x3 constant,results in:A)a decrease of 3 units on average in the value of y.
B)an increase of 8 units in the value of y.
C)an increase of 3 units on average in the value of y.
D)None of these choices.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
57
In a multiple regression analysis,there are 20 data points and 4 independent variables,and the sum of the squared differences between observed and predicted values of y is 180.The standard error of estimate will be:
A)9.000
B)6.708
C)3.464
D)3.000
A)9.000
B)6.708
C)3.464
D)3.000

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
58
In a multiple regression model,the probability distribution of the error variable ε is assumed to be:
A)normal.
B)non-normal.
C)positively skewed.
D)negatively skewed.
A)normal.
B)non-normal.
C)positively skewed.
D)negatively skewed.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
59
For a multiple regression model,the total variation in y can be expressed as:
A)SSE − SSR.
B)SSR − SSE.
C)SSR + SSE.
D)SSR / SSE.
A)SSE − SSR.
B)SSR − SSE.
C)SSR + SSE.
D)SSR / SSE.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
60
In testing the validity of a multiple regression model in which there are four independent variables,the null hypothesis is:
A)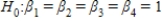 .
.
B)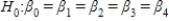 .
.
C)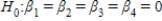 .
.
D)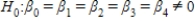
)
A)
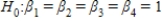 .
.B)
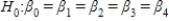 .
.C)
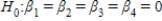 .
.D)
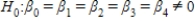
)

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
61
Life Expectancy
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} Interpret the coefficient b1.
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3
 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} Interpret the coefficient b1.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
62
Student's Final Grade
A statistics professor investigated some of the factors that affect an individual student's final grade in her course.She proposed the multiple regression model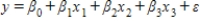 ,where y is the final grade (out of 100 points),x1 is the number of lectures skipped,x2 is the number of late assignments,and x3 is the midterm exam score (out of 100).The professor recorded the data for 50 randomly selected students.The computer output is shown below. THE REGRESSION EQUATION IS
,where y is the final grade (out of 100 points),x1 is the number of lectures skipped,x2 is the number of late assignments,and x3 is the midterm exam score (out of 100).The professor recorded the data for 50 randomly selected students.The computer output is shown below. THE REGRESSION EQUATION IS 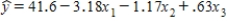
 S = 13.74 R−Sq = 30.0% ANALYSIS OF VARIANCE
S = 13.74 R−Sq = 30.0% ANALYSIS OF VARIANCE 
{Student's Final Grade Narrative} What is the coefficient of determination? What does this statistic tell you?
A statistics professor investigated some of the factors that affect an individual student's final grade in her course.She proposed the multiple regression model
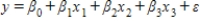 ,where y is the final grade (out of 100 points),x1 is the number of lectures skipped,x2 is the number of late assignments,and x3 is the midterm exam score (out of 100).The professor recorded the data for 50 randomly selected students.The computer output is shown below. THE REGRESSION EQUATION IS
,where y is the final grade (out of 100 points),x1 is the number of lectures skipped,x2 is the number of late assignments,and x3 is the midterm exam score (out of 100).The professor recorded the data for 50 randomly selected students.The computer output is shown below. THE REGRESSION EQUATION IS 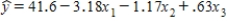
 S = 13.74 R−Sq = 30.0% ANALYSIS OF VARIANCE
S = 13.74 R−Sq = 30.0% ANALYSIS OF VARIANCE 
{Student's Final Grade Narrative} What is the coefficient of determination? What does this statistic tell you?

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
63
Life Expectancy
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} What is the adjusted coefficient of determination in this situation? What does this statistic tell you?
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3
 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} What is the adjusted coefficient of determination in this situation? What does this statistic tell you?

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
64
The computer output for the multiple regression model 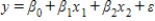 is shown below.However,because of a printer malfunction some of the results are not shown.These are indicated by the boldface letters a to i.Fill in the missing results (up to three decimal places).
is shown below.However,because of a printer malfunction some of the results are not shown.These are indicated by the boldface letters a to i.Fill in the missing results (up to three decimal places).  S = d
S = d
R−Sq = e
ANALYSIS OF VARIANCE
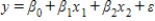 is shown below.However,because of a printer malfunction some of the results are not shown.These are indicated by the boldface letters a to i.Fill in the missing results (up to three decimal places).
is shown below.However,because of a printer malfunction some of the results are not shown.These are indicated by the boldface letters a to i.Fill in the missing results (up to three decimal places).  S = d
S = dR−Sq = e
ANALYSIS OF VARIANCE


Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
65
Life Expectancy
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} Is there sufficient evidence at the 5% significance level to infer that the number of points that the individual's blood pressure exceeded the recommended value and the age at death are negatively linearly related?
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3
 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} Is there sufficient evidence at the 5% significance level to infer that the number of points that the individual's blood pressure exceeded the recommended value and the age at death are negatively linearly related?

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
66
We test an individual coefficient in a multiple regression model using a(n)_________ test.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
67
Consider the following statistics of a multiple regression model: Total variation in y = 1000,SSE = 300,n = 50,and k = 4.
a.Determine the standard error of estimate.
b.Determine the coefficient of determination.
c.Determine the F-statistic.
a.Determine the standard error of estimate.
b.Determine the coefficient of determination.
c.Determine the F-statistic.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
68
Life Expectancy
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} What is the coefficient of determination? What does this statistic tell you?
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3
 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} What is the coefficient of determination? What does this statistic tell you?

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
69
Some of the requirements for the error variable in a multiple regression model are that the probability distribution is ____________________ with a mean of ____________________.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
70
Life Expectancy
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} Is there enough evidence at the 5% significance level to infer that the cholesterol level and the age at death are negatively linearly related?
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3
 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} Is there enough evidence at the 5% significance level to infer that the cholesterol level and the age at death are negatively linearly related?

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
71
Life Expectancy
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} Interpret the coefficient b3.
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3
 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} Interpret the coefficient b3.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
72
Consider the following statistics of a multiple regression model: n = 25,k = 5,b1 = −6.31,and sε = 2.98.Can we conclude at the 1% significance level that x1 and y are linearly related?

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
73
Life Expectancy
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} Is there enough evidence at the 1% significance level to infer that the average number of hours of exercise per week and the age at death are linearly related?
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3
 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} Is there enough evidence at the 1% significance level to infer that the average number of hours of exercise per week and the age at death are linearly related?

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
74
The coefficient of determination ____________________ for degrees of freedom takes into account the sample size and the number of independent variables when assessing model fit.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
75
When there is more than one independent variable in a regression model,we refer to the graphical depiction of the equation as a(n)____________________ rather than as a straight line.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
76
Some of the requirements for the error variable in a multiple regression model are that the standard deviation is a(n)____________________ and the errors are ____________________.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
77
Life Expectancy
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} Is there enough evidence at the 5% significance level to infer that the model is useful in predicting length of life?
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3
 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} Is there enough evidence at the 5% significance level to infer that the model is useful in predicting length of life?

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
78
A(n)____________________ value of the F-test statistic indicates that the multiple regression model is valid.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
79
The total variation in y is equal to SSR + ____________________.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck
80
Life Expectancy
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} Interpret the coefficient b2.
An actuary wanted to develop a model to predict how long individuals will live.After consulting a number of physicians,she collected the age at death (y),the average number of hours of exercise per week (x1),the cholesterol level (x2),and the number of points that the individual's blood pressure exceeded the recommended value (x3).A random sample of 40 individuals was selected.The computer output of the multiple regression model is shown below. THE REGRESSION EQUATION IS y = 55.8 + 1.79x1− 0.021x2− 0.061x3
 S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE
S = 9.47 R−Sq = 22.5% ANALYSIS OF VARIANCE 
{Life Expectancy Narrative} Interpret the coefficient b2.

Unlock Deck
Unlock for access to all 160 flashcards in this deck.
Unlock Deck
k this deck


