Deck 13: Loan Amortization; Mortgages
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/188
Play
Full screen (f)
Deck 13: Loan Amortization; Mortgages
1
The interest rate on a $50,000 loan is 7.6% compounded semi-annually. Quarterly payments will pay off the loan in ten years.
a) Calculate the interest component of Payment 8.
b) Calculate the principal component of Payment 33.
c) Calculate the total interest in Payments 21 to 30 inclusive.
d) Calculate the reduction of principal in Year 3.
a) Calculate the interest component of Payment 8.
b) Calculate the principal component of Payment 33.
c) Calculate the total interest in Payments 21 to 30 inclusive.
d) Calculate the reduction of principal in Year 3.
a) $822.74; b) $1,542.15; c) $4,474.70; d) $4,055.64
2
Golden Dragon Restaurant obtained a $9,000 loan at 5% compounded annually to replace some kitchen equipment. Prepare a complete amortization schedule if payments of $1,800 (except for a smaller final payment) are made semi-annually.
(See the Instructor's Manual for the schedule)
3
Golden Dragon Restaurant obtained a $9,000 loan at 5% compounded annually to replace some kitchen equipment. Prepare a complete amortization schedule if the loan is to be repaid by semi-annual payments over a three-year term. Calculate the total interest charges.
$793.68 (See the Instructor's Manual for the schedule)
4
Valley Produce received $50,000 in vendor financing at 3.8% compounded semi-annually for the purchase of harvesting machinery. The contract requires equal annual payments for seven years to repay the debt. Construct the amortization schedule for the debt. How much interest will be paid over the seven-year term?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
5
Dr. Alvano borrowed $8,000 at 8% compounded quarterly to purchase a new X-Ray machine for his clinic. The agreement requires quarterly payments during a two-year amortization period. Suppose that the loan permits an additional prepayment of principal on any scheduled payment date. Prepare an amortization schedule that reflects a prepayment of $1,000 with the third scheduled payment.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
6
The interest rate on a $14,000 loan is 5.4% compounded semi-annually. Semi-annual payments will pay off the loan in seven years.
a) Calculate the interest component of Payment 10.
b) Calculate the principal component of Payment 3.
c) Calculate the interest paid in Year 6.
d) How much do Payments 3 to 6 inclusive reduce the principal balance?
a) Calculate the interest component of Payment 10.
b) Calculate the principal component of Payment 3.
c) Calculate the interest paid in Year 6.
d) How much do Payments 3 to 6 inclusive reduce the principal balance?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
7
A five-year loan of $25,000 at 7.2% compounded quarterly requires quarterly payments.
a) Calculate the interest component of Payment 10.
b) Calculate the principal component of Payment 13.
c) Calculate the total interest in Payments 5 to 10 inclusive.
d) Calculate the principal paid in Year 4.
a) Calculate the interest component of Payment 10.
b) Calculate the principal component of Payment 13.
c) Calculate the total interest in Payments 5 to 10 inclusive.
d) Calculate the principal paid in Year 4.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
8
Dr. Alvano borrowed $8,000 at 8% compounded quarterly to purchase a new X-ray machine for his clinic. The agreement requires quarterly payments of $1,000 (except for a smaller final payment). Prepare the full amortization schedule for the loan. Calculate the total interest charges.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
9
Valley Produce received $50,000 in vendor financing at 3.8% compounded semi-annually for the purchase of harvesting machinery. The contract requires annual payments of $10,000 (except for a smaller final payment). Construct the complete amortization schedule for the debt. How much interest will be paid over the entire life of the loan?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
10
Dr. Alvano borrowed $8,000 at 10% compounded quarterly to purchase a new X-ray machine for his clinic. The agreement requires quarterly payments during a two-year amortization period. Prepare the full amortization schedule for the loan. Calculate the total interest charges.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
11
Cloverdale Nurseries obtained a $60,000 loan at 7.5% compounded monthly to build an additional greenhouse. Construct a partial amortization schedule for payments of $1,000 per month (except for a smaller final payment) showing details of the first two payments, Payments 56 and 57, and the last two payments.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
12
Cloverdale Nurseries obtained a $60,000 loan at 7.5% compounded monthly to build an additional greenhouse. Monthly payments were calculated to amortize the loan over six years. Construct a partial amortization schedule showing details of the first two payments, Payments 43 and 44, and the last two payments.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
13
A $125,000 loan at 6.0% compounded semi-annually will be repaid by monthly payments over a 20-year amortization period.
a) Calculate the interest component of Payment 188.
b) Calculate the principal component of Payment 101.
c) Calculate the reduction of principal in Year 1.
d) Calculate the reduction of principal in Year 20.
a) Calculate the interest component of Payment 188.
b) Calculate the principal component of Payment 101.
c) Calculate the reduction of principal in Year 1.
d) Calculate the reduction of principal in Year 20.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
14
Jean and Walter Pereira financed the addition of a swimming pool using a $24,000 home improvement loan from their bank. Monthly payments were based on an interest rate of 5.2% compounded semi-annually and a five-year amortization. Construct a partial amortization schedule showing details of the first two payments, Payments 30 and 31, and the last two payments. What total interest will the Pereiras pay over the life of the loan?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
15
A $40,000 loan at 6.6% compounded monthly will be repaid by monthly payments over ten years.
a) Calculate the interest component of Payment 35.
b) Calculate the principal component of Payment 63.
c) Calculate the reduction of principal in Year 1.
d) Calculate the reduction of principal in Year 10.
a) Calculate the interest component of Payment 35.
b) Calculate the principal component of Payment 63.
c) Calculate the reduction of principal in Year 1.
d) Calculate the reduction of principal in Year 10.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
16
Monica bought a $1,250 laptop computer for 20% down, with the balance to be paid with interest at 15% compounded monthly in six equal monthly payments. Construct the full amortization schedule for the debt. Calculate the total interest paid.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
17
Jean and Walter Pereira financed the addition of a swimming pool using a $24,000 home improvement loan from their bank. Monthly payments of $500 (except for a smaller final payment) include interest at 5.2% compounded semi-annually. Construct a partial amortization schedule showing details of the first two payments, Payments 28 and 29, and the last two payments. What total interest will the Pereiras pay over the life of the loan?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
18
The monthly payments on a $15,000 loan at 6.0% compounded monthly are $275.
a) Calculate the interest component of Payment 13.
b) Calculate the principal component of Payment 44.
c) Calculate the final payment.
a) Calculate the interest component of Payment 13.
b) Calculate the principal component of Payment 44.
c) Calculate the final payment.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
19
Monica bought a $1250 laptop computer for 20% down and payments of $200 per month (except for a smaller final payment) including interest at 15% compounded monthly. Construct the full amortization schedule for the debt. Calculate the total interest paid.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
20
Cloverdale Nurseries obtained a $60,000 loan at 7.5% compounded monthly to build an additional greenhouse. Monthly payments were calculated to amortize the loan over six years. Construct a partial amortization schedule showing details of the first two payments, Payments 43 and 44, and the last two payments.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
21
The Graftons can afford a maximum mortgage payment of $1,000 per month. The current interest rate is 5.2% compounded semi-annually. What is the maximum mortgage loan they can afford if the amortization period is:
a) 15 years? b) 20 years? c) 25 years? d) 30 years?
a) 15 years? b) 20 years? c) 25 years? d) 30 years?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
22
The Tarkanians can afford a maximum mortgage payment of $1,000 per month. What is the maximum mortgage loan they can afford if the amortization period is 25 years and the interest rate is:
a) 5.5% compound semi-annually?
b) 6.5% compounded semi-annually?
c) 7.5% compounded semi-annually?
a) 5.5% compound semi-annually?
b) 6.5% compounded semi-annually?
c) 7.5% compounded semi-annually?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
23
Using the Composition of Loan Payments Chart An interactive chart for investigating the composition of loan payments is provided in the textbook's Online Learning Centre (OLC). Go to the Student Edition of the OLC. In the navigation bar, select "Chapter 14" in the drop-down box. In the list of resources for Chapter 13, select "Links in Textbook" and then click on the link named "Composition of Loan Payments."
The chart provides cells for entering the essential information about a loan (PV, j, m, PMT, and payments/year). You can then compare the composition (interest and principal components) of any two payments. Simply enter the serial numbers of the two payments and then click on the "Submit" button. Two bar diagrams provide a visual comparison of the interest and principal components. The actual numerical values are also displayed.
Consider a $120,000 mortgage loan at 6.5% compounded semi-annually. Monthly payments of $800 will pay off the loan in 25 years and 4 months.
a) How much more interest is paid by the 20th payment than the 220th payment?
b) How long does it take before the interest component of a payment drops below 50%?
c) Which payment number is closest to being comprised of: (i) 75% interest? (ii) 25% interest?
d) Which payment number comes closest to having a mix of principal and interest that is the opposite of the first payment's mix?
e) Which payment number comes closest to having double the principal component of the 5th payment?
f) Which payment number comes closest to having half the interest component of the 10th payment?
The chart provides cells for entering the essential information about a loan (PV, j, m, PMT, and payments/year). You can then compare the composition (interest and principal components) of any two payments. Simply enter the serial numbers of the two payments and then click on the "Submit" button. Two bar diagrams provide a visual comparison of the interest and principal components. The actual numerical values are also displayed.
Consider a $120,000 mortgage loan at 6.5% compounded semi-annually. Monthly payments of $800 will pay off the loan in 25 years and 4 months.
a) How much more interest is paid by the 20th payment than the 220th payment?
b) How long does it take before the interest component of a payment drops below 50%?
c) Which payment number is closest to being comprised of: (i) 75% interest? (ii) 25% interest?
d) Which payment number comes closest to having a mix of principal and interest that is the opposite of the first payment's mix?
e) Which payment number comes closest to having double the principal component of the 5th payment?
f) Which payment number comes closest to having half the interest component of the 10th payment?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
24
A five-year loan of $20,000 at 6.8% compounded quarterly requires monthly payments.
a) Calculate the interest component of Payment 47.
b) Calculate the principal component of Payment 21.
c) Calculate the interest paid in Year 2.
d) How much do Payments 40 to 45 inclusive reduce the principal balance?
a) Calculate the interest component of Payment 47.
b) Calculate the principal component of Payment 21.
c) Calculate the interest paid in Year 2.
d) How much do Payments 40 to 45 inclusive reduce the principal balance?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
25
The interest rate on a $100,000 loan is 7.2% compounded semi-annually. The monthly payments on the loan are $700.
a) Calculate the interest component of Payment 221.
b) Calculate the principal component of Payment 156.
c) Calculate the final payment.
a) Calculate the interest component of Payment 221.
b) Calculate the principal component of Payment 156.
c) Calculate the final payment.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
26
Quarterly payments of $3,000 are required on an $80,000 loan at 8.0% compounded quarterly.
a) Calculate the interest component of Payment 30.
b) Calculate the principal component of Payment 9.
c) Calculate the final payment.
a) Calculate the interest component of Payment 30.
b) Calculate the principal component of Payment 9.
c) Calculate the final payment.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
27
A 10-year annuity providing a rate of return of 5.6% compounded quarterly was purchased for $25,000. The annuity makes payments at the end of each quarter.
a) How much of the twenty-fifth payment is interest?
b) What is the principal portion of the thirteenth payment?
c) What is the total interest in Payments 11 to 20 inclusive?
d) How much is the principal reduction in the second year?
e) What is the final payment?
a) How much of the twenty-fifth payment is interest?
b) What is the principal portion of the thirteenth payment?
c) What is the total interest in Payments 11 to 20 inclusive?
d) How much is the principal reduction in the second year?
e) What is the final payment?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
28
The interest rate for the first three years of an $150,000 mortgage loan is 6.9% compounded semi-annually. Monthly payments are calculated using a 25-year amortization.
a) What will be the principal balance at the end of the three-year term?
b) What will the monthly payments be if the loan is renewed at 5.5% compounded semi-annually (and the original amortization period is continued)?
a) What will be the principal balance at the end of the three-year term?
b) What will the monthly payments be if the loan is renewed at 5.5% compounded semi-annually (and the original amortization period is continued)?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
29
Guy borrowed $8,000 at 7.8% compounded monthly and agreed to make quarterly payments of $500 (except for a smaller final payment).
a) How much of the eleventh payment will be interest?
b) What will be the principal component of the sixth payment?
c) How much interest will be paid by Payments 3 to 9 inclusive?
d) How much will the principal be reduced in the third year?
e) What will be the final payment?
a) How much of the eleventh payment will be interest?
b) What will be the principal component of the sixth payment?
c) How much interest will be paid by Payments 3 to 9 inclusive?
d) How much will the principal be reduced in the third year?
e) What will be the final payment?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
30
The Switzers are nearing the end of the first five-year term of a $200,000 mortgage loan with a 25-year amortization. The interest rate has been 4.5% compounded semi-annually for the initial term. How much will their monthly payments increase if the interest rate upon renewal is 7.5% compounded semi-annually?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
31
Elkford Logging's bank will fix the interest rate on a $60,000 loan at 4.2% compounded monthly for the first four-year term of an eight-year amortization period. Monthly payments are required on the loan.
a) If the prevailing interest rate on four-year loans at the beginning of the second term is 6% compounded monthly, what will be the monthly payments for the last four years?
b) What will be the interest portion of the twenty-third payment?
c) Calculate the principal portion of the fifty-third payment
a) If the prevailing interest rate on four-year loans at the beginning of the second term is 6% compounded monthly, what will be the monthly payments for the last four years?
b) What will be the interest portion of the twenty-third payment?
c) Calculate the principal portion of the fifty-third payment

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
32
A $37,000 loan at 8.2% compounded semi-annually is to be repaid by equal semi-annual payments over 10 years.
a) What will be the principal component of the sixth payment?
b) What will be the interest component of the sixteenth payment?
c) How much will Payments 6 to 15 inclusive reduce the principal?
d) How much interest will be paid in the third year?
e) What will be the final payment?
a) What will be the principal component of the sixth payment?
b) What will be the interest component of the sixteenth payment?
c) How much will Payments 6 to 15 inclusive reduce the principal?
d) How much interest will be paid in the third year?
e) What will be the final payment?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
33
The calculated monthly payment on a loan amortized over five years is rounded up by 0.2 cents to get to the nearest cent.
a) Will the adjusted final payment be more than or less than the regular payment?
b) Will the difference between the regular and the final payment be (pick one): (i) more than (ii) less than or (iii) equal to 0.2 cents? 60 = 12 cents? Explain.
a) Will the adjusted final payment be more than or less than the regular payment?
b) Will the difference between the regular and the final payment be (pick one): (i) more than (ii) less than or (iii) equal to 0.2 cents? 60 = 12 cents? Explain.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
34
The interest rate for the first five years of a $27,000 mortgage loan was 7.25% compounded semi-annually. The monthly payments computed for a 10-year amortization were rounded to the next higher $10.
a) Calculate the principal balance at the end of the first term.
b) Upon renewal at 6.75% compounded semi-annually, monthly payments were calculated for a 5-year amortization and again rounded up to the next $10. What will be the amount of the last payment?
a) Calculate the principal balance at the end of the first term.
b) Upon renewal at 6.75% compounded semi-annually, monthly payments were calculated for a 5-year amortization and again rounded up to the next $10. What will be the amount of the last payment?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
35
A $100,000 mortgage loan at 6.3% compounded semi-annually has a 25-year amortization period.
a) Calculate the monthly payment.
b) If the interest rate were 1% lower (that is, 5.3% compounded semi-annually), what loan amount would result in the same monthly payment?
a) Calculate the monthly payment.
b) If the interest rate were 1% lower (that is, 5.3% compounded semi-annually), what loan amount would result in the same monthly payment?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
36
An annuity paying $1400 at the end of each month (except for a smaller final payment) was purchased with $225,000 that had accumulated in an RRSP. The annuity provides a semi-annually compounded rate of return of 5.2%.
a) What amount of principal will be included in Payment 137?
b) What will be the interest portion of Payment 204?
c) How much will the principal be reduced by Payments 145 to 156 inclusive?
d) How much interest will be paid in the twentieth year?
e) What will be the final payment?
a) What amount of principal will be included in Payment 137?
b) What will be the interest portion of Payment 204?
c) How much will the principal be reduced by Payments 145 to 156 inclusive?
d) How much interest will be paid in the twentieth year?
e) What will be the final payment?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
37
Christina has just borrowed $12,000 at 7% compounded semi-annually. Since she expects to receive a $10,000 inheritance in two years when she turns 25, she has arranged with her credit union to make monthly payments that will reduce the principal balance to exactly $10,000 in two years.
a) What monthly payments will she make?
b) What will be the interest portion of the ninth payment?
c) Determine the principal portion of the sixteenth payment.
a) What monthly payments will she make?
b) What will be the interest portion of the ninth payment?
c) Determine the principal portion of the sixteenth payment.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
38
Ms. Esperanto obtained a $40,000 home equity loan at 7.5% compounded monthly.
a) What will she pay monthly if the amortization period is 15 years?
b) How much of the payment made at the end of the fifth year will go towards principal and how much will go towards interest?
c) What will be the balance on the loan after five years?
d) How much interest did she pay during the fifth year?
a) What will she pay monthly if the amortization period is 15 years?
b) How much of the payment made at the end of the fifth year will go towards principal and how much will go towards interest?
c) What will be the balance on the loan after five years?
d) How much interest did she pay during the fifth year?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
39
The Melnyks are nearing the end of the first three-year term of a $200,000 mortgage loan with a 20-year amortization. The interest rate has been 7.7% compounded semi-annually for the initial term. How much will their monthly payments decrease if the interest rate upon renewal is 6.7% compounded semi-annually?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
40
Guy borrowed $8,000 at 7.8% compounded monthly and agreed to repay the loan in equal quarterly payments over four years.
a) How much of the fifth payment will be interest?
b) What will be the principal component of the eleventh payment?
c) How much interest will be paid by Payments 5 to 12 inclusive?
d) How much will the principal be reduced in the second year?
e) What will be the final payment?
a) How much of the fifth payment will be interest?
b) What will be the principal component of the eleventh payment?
c) How much interest will be paid by Payments 5 to 12 inclusive?
d) How much will the principal be reduced in the second year?
e) What will be the final payment?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
41
Givens, Hong, and Partners obtained a $7,000 term loan at 8. 5% compounded annually for new boardroom furniture. Prepare a complete amortization schedule in which the loan is repaid by equal semi-annual payments over three years.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
42
An annuity providing a rate of return of 4.8% compounded monthly was purchased for $45,000. The annuity pays $400 at the end of each month.
a) How much of the 37th payment will be interest?
b) What will be the principal portion of the 92nd payment?
c) How much interest will be paid by Payments 85 to 96 inclusive?
d) How much principal will be repaid in the fifth year?
e) What will be the final payment?
a) How much of the 37th payment will be interest?
b) What will be the principal portion of the 92nd payment?
c) How much interest will be paid by Payments 85 to 96 inclusive?
d) How much principal will be repaid in the fifth year?
e) What will be the final payment?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
43
A $175,000 mortgage at 6.6% compounded semi-annually with a 25-year amortization requires monthly payments. The mortgage allows the borrower to prepay up to 10% of the original principal once each year. How much will the amortization period be shortened if, on the first anniversary of the mortgage, the borrower makes (in addition to the regular payment) a prepayment of:
a) $10,000? b) $20,000?
a) $10,000? b) $20,000?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
44
Monthly payments on a $150,000 mortgage are based on an interest rate of 4.9% compounded semi-annually and a 30-year amortization. If a $5,000 prepayment is made along with the 32nd payment,
a) How much will the amortization period be shortened?
b) What will be the principal balance after four years?
a) How much will the amortization period be shortened?
b) What will be the principal balance after four years?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
45
A 20-year annuity was purchased with $180,000 that had accumulated in an RRSP. The annuity provides a semi-annually compounded rate of return of 5% and makes equal month-end payments.
a) What will be the principal portion of Payment 134?
b) What will be the interest portion of Payment 210?
c) How much will the loan's balance be reduced by Payments 75 to 100 inclusive?
d) How much interest will be paid in the sixth year?
a) What will be the principal portion of Payment 134?
b) What will be the interest portion of Payment 210?
c) How much will the loan's balance be reduced by Payments 75 to 100 inclusive?
d) How much interest will be paid in the sixth year?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
46
Metro Construction received $60,000 in vendor financing at 10.5% compounded semi-annually for the purchase of a loader. The contract requires semi-annual payments of $10,000 until the debt is paid off. Suppose that the loan permits an additional prepayment of principal on any scheduled payment date. Prepare another amortization schedule that reflects a prepayment of $5,000 with the third scheduled payment. How much interest is saved as a result of the prepayment?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
47
The interest rate for the first five years of a $165,000 mortgage loan is 6.25% compounded semi-annually. Monthly payments are calculated using a 20-year amortization.
a) What will be the principal balance at the end of the five-year term?
b) What will be the new payments if the loan is renewed at 5.5% compounded semi-annually (and the original amortization period is continued)?
a) What will be the principal balance at the end of the five-year term?
b) What will be the new payments if the loan is renewed at 5.5% compounded semi-annually (and the original amortization period is continued)?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
48
The MacLellans originally chose to make payments of $1600 per month on a $138,000 mortgage written at 7.4% compounded semi-annually for the first five years. After three years they exercised the right under the mortgage contract to increase the payments by 10%.
a) If the interest rate does not change, when will they extinguish the mortgage debt?
b) What will be the principal balance at the end of the five-year term?
a) If the interest rate does not change, when will they extinguish the mortgage debt?
b) What will be the principal balance at the end of the five-year term?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
49
Marge and Homer Sampson have saved $90,000 toward the purchase of their first home. Allowing $7,000 for legal costs and moving expenses, they have $83,000 available for a down payment.
a) Based only on a loan-to-value ratio of 80%, what is the maximum purchase price they can consider?
b) After thorough investigation, the Sampsons made a $360,000 offer on a townhouse subject to arranging financing. Next they met with their banker. With an $88,000 down payment, the Sampsons will need a mortgage loan of $272,000. The current interest rate on a five-year term fixed-rate mortgage with a 25-year amortization is 5.4% compounded semi-annually. The banker gathered data for calculating the Sampsons' GDS and TDS ratios. Annual property taxes will be $3000. Annual heating costs will be about $2400. The Sampsons make monthly payments of $800 on a car loan ($14,000 balance). Their gross monthly income is $7000. Calculate the GDS and TDS ratios for the Sampsons.
c) Note that the Sampsons meet the GDS criterion (_32%) but exceed the TDS limit (40%). The item causing the problem is the $800 per month car payment. Suppose the Sampsons use $14,000 of their down-payment savings to pay off the car loan. They will still have enough to make the minimum down payment (0.20 × $360,000 = $72,000) but will have to increase the mortgage loan by $14,000 to $286,000. Recalculate the GDS and TDS ratios. Do the Sampsons satisfy all three ratios by taking this approach?
a) Based only on a loan-to-value ratio of 80%, what is the maximum purchase price they can consider?
b) After thorough investigation, the Sampsons made a $360,000 offer on a townhouse subject to arranging financing. Next they met with their banker. With an $88,000 down payment, the Sampsons will need a mortgage loan of $272,000. The current interest rate on a five-year term fixed-rate mortgage with a 25-year amortization is 5.4% compounded semi-annually. The banker gathered data for calculating the Sampsons' GDS and TDS ratios. Annual property taxes will be $3000. Annual heating costs will be about $2400. The Sampsons make monthly payments of $800 on a car loan ($14,000 balance). Their gross monthly income is $7000. Calculate the GDS and TDS ratios for the Sampsons.
c) Note that the Sampsons meet the GDS criterion (_32%) but exceed the TDS limit (40%). The item causing the problem is the $800 per month car payment. Suppose the Sampsons use $14,000 of their down-payment savings to pay off the car loan. They will still have enough to make the minimum down payment (0.20 × $360,000 = $72,000) but will have to increase the mortgage loan by $14,000 to $286,000. Recalculate the GDS and TDS ratios. Do the Sampsons satisfy all three ratios by taking this approach?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
50
A $25,000 home improvement (mortgage) loan charges interest at 6.6% compounded monthly for a three-year term. Monthly payments are based on a 10-year amortization and rounded up to the next $10. What will be the principal balance at the end of the first term?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
51
Five years ago, Ms. Halliday received a mortgage loan from the Bank of Nova Scotia for $60,000 at 7.8% compounded semi-annually for a five-year term. Monthly payments were based on a 25-year amortization. The bank is agreeable to renewing the loan for another five-year term at 5.8% compounded semi-annually. Calculate the principal reduction that will occur in the second five-year term if:
a) The payments are recalculated based on the new interest rate and a continuation of the original 25-year amortization.
b) Ms. Halliday continues to make the same payments as she made for the first five years (resulting in a reduction of the amortization period).
a) The payments are recalculated based on the new interest rate and a continuation of the original 25-year amortization.
b) Ms. Halliday continues to make the same payments as she made for the first five years (resulting in a reduction of the amortization period).

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
52
After three years of the first five-year term at 6.3% compounded semi-annually, Dean and Cindy decide to take advantage of the privilege of increasing the payments on their $200,000 mortgage loan by 10%. The monthly payments were originally calculated for a 30-year amortization.
a) How much will the amortization period be shortened?
b) What will be the principal balance at the end of the five-year term?
a) How much will the amortization period be shortened?
b) What will be the principal balance at the end of the five-year term?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
53
A $200,000 mortgage at 6.9% compounded semi-annually with a 25-year amortization requires monthly payments. The mortgage entitles the borrower to increase the regular payment by up to 15% once each year. How much will the amortization period be shortened if, after the 12th payment, the payments are increased by:
a) 7.5%? b) 15%?
a) 7.5%? b) 15%?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
54
A $200,000 mortgage at 6.2% compounded semi-annually with a 25-year amortization requires monthly payments. The mortgage allows the borrower to "double up" on a payment once each year. How much will the amortization period be shortened if the mortgagor doubles the tenth payment?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
55
Niagara Haulage obtained an $80,000 loan at 7.2% compounded monthly to build a storage shed. Construct a partial amortization schedule for payments of $1,000 per month showing details of the first two payments, Payments 41 and 42, and the last two payments.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
56
Metro Construction received $60,000 in vendor financing at 6.5% compounded semi-annually for the purchase of a loader. The contract requires semi-annual payments of $7,500 until the debt is paid off. Construct the complete amortization schedule for the debt. How much total interest will be paid over the life of the loan?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
57
If the loan payments and interest rate remain unchanged, will it take longer to reduce the balance from $20,000 to $10,000 than to reduce the balance from $10,000 to $0? Explain briefly.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
58
A $140,000 mortgage loan charges interest at 6.6% compounded monthly for a four-year term. Monthly payments were calculated for a 15-year amortization and then rounded up to the next higher $10.
a) What will be the principal balance at the end of the first term?
b) What will the monthly payments be on renewal for a three-year term if it is calculated for an interest rate of 7.2% compounded monthly and an 11-year amortization period, but again rounded to the next higher $10?
a) What will be the principal balance at the end of the first term?
b) What will the monthly payments be on renewal for a three-year term if it is calculated for an interest rate of 7.2% compounded monthly and an 11-year amortization period, but again rounded to the next higher $10?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
59
A $28,000 loan at 8% compounded quarterly is to be repaid by equal quarterly payments over a seven-year term.
a) What will be the principal component of the sixth payment?
b) What will be the interest portion of the 22nd payment?
c) How much will the loan's balance be reduced by Payments 10 to 15 inclusive?
d) How much interest will be paid in the second year?
a) What will be the principal component of the sixth payment?
b) What will be the interest portion of the 22nd payment?
c) How much will the loan's balance be reduced by Payments 10 to 15 inclusive?
d) How much interest will be paid in the second year?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
60
Jessica bought an $1,150 television set for 25% down and the balance to be paid with interest at 11.25% compounded monthly in six equal monthly payments. Construct the full amortization schedule for the debt. Calculate the total interest paid.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
61
Lucille borrowed $21,500 for office equipment. The loan requires quarterly payments over two years at 6.5% compounded semi-annually. Construct a full amortization schedule for the loan. Show the total interest paid.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
62
Valley Produce received $50,000 in vendor financing at 7.8% compounded semi-annually for the purchase of harvesting machinery. The contract requires equal annual payments for seven years to repay the debt. Suppose that the loan permits an additional prepayment of principal on any scheduled payment date. Prepare an amortization schedule that reflects a prepayment of $10,000 with the second scheduled payment. How much interest is saved as a result of the prepayment?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
63
A mortgage contract for $145,000 written 10 years ago is just at the end of its second five-year term. The interest rates were 8% compounded semi-annually for the first term and 7% compounded semi-annually for the second term. If monthly payments throughout have been based on a 25-year amortization, calculate the principal balance at the end of the second term.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
64
A mortgage of $300,000 is amortized over 20 years at 5.25% compounded quarterly. What is the outstanding balance after 10 years?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
65
A $200,000 mortgage at 5.5% compounded monthly is amortized over 20 years. What is the amount of the monthly payment?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
66
Semi-annual payments are required on an $80,000 loan at 8.0% compounded annually. The loan has an amortization period of 15 years.
a) Calculate the interest component of Payment 5.
b) Calculate the principal component of Payment 17.
c) Calculate the interest paid in Year 1.
d) Calculate the interest paid in Year 14.
a) Calculate the interest component of Payment 5.
b) Calculate the principal component of Payment 17.
c) Calculate the interest paid in Year 1.
d) Calculate the interest paid in Year 14.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
67
The interest rate on a $6,400 loan is 10% compounded semi-annually. If the loan is to be repaid by monthly payments over a four-year term, prepare a partial amortization schedule showing details of the first two payments, Payments 34 and 35, and the last two payments.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
68
Larissa bought a stereo for $5,000. She made a down payment of $1,000, and financed the balance with monthly payments over four years at 8.5% compounded quarterly. Construct a partial amortization schedule showing details of the first two payments, payments 22 and 23, and the last two payments. How much interest did Larissa pay in total?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
69
Jakob borrowed $27,000 for a car. He is making monthly payments of $494.81 at 3.8% compounded monthly. Construct a partial amortization schedule showing details of the first two payments, payments 33 and 34, and the last two payments.

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
70
A 25-year annuity was purchased with $225,000 that had accumulated in a Registered Retirement Savings Plan (RRSP). The annuity provides a semi-annually compounded rate of return of 5.2% and makes equal month-end payments.
a) What amount of principal will be included in Payment 206?
b) What will be the interest portion of Payment 187?
c) How much will Payments 50 to 100 inclusive reduce the principal balance?
d) How much interest will be paid in the fourteenth year?
e) What will be the final payment?
a) What amount of principal will be included in Payment 206?
b) What will be the interest portion of Payment 187?
c) How much will Payments 50 to 100 inclusive reduce the principal balance?
d) How much interest will be paid in the fourteenth year?
e) What will be the final payment?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
71
A $16,000 loan is to be amortized by monthly payments over a five-year period. The interest rate on the loan is 10.8% compounded monthly.
a) What is the interest portion of the 29th payment?
b) Determine the principal portion of the 46th payment.
c) How much will the principal be reduced in the second year?
d) How much interest will be paid in the third year?
a) What is the interest portion of the 29th payment?
b) Determine the principal portion of the 46th payment.
c) How much will the principal be reduced in the second year?
d) How much interest will be paid in the third year?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
72
Valley Produce received $50,000 in vendor financing at 3.8% compounded semi-annually for the purchase of harvesting machinery. The contract requires equal annual payments for seven years to repay the debt. Suppose that the loan permits an additional prepayment of principal on any scheduled payment date. Prepare an amortization schedule that reflects a prepayment of $10,000 with the second scheduled payment. How much interest is saved as a result of the prepayment?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
73
The interest rate for the first five years of a $142,000 mortgage is 5.8% compounded semi-annually. Monthly payments are based on a 25-year amortization. If a $3,000 prepayment is made at the end of the third year:
a) How much will the amortization period be shortened?
b) What will be the principal balance at the end of the five-year term?
a) How much will the amortization period be shortened?
b) What will be the principal balance at the end of the five-year term?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
74
After two years of the first five-year term at 6.7% compounded semi-annually, Dan and Laurel decide to take advantage of the privilege of increasing the payments on their $110,000 mortgage loan by 10%. The monthly payments were originally calculated for a 25-year amortization.
a) How much will the amortization period be shortened?
b) What will be the principal balance at the end of the five-year term?
a) How much will the amortization period be shortened?
b) What will be the principal balance at the end of the five-year term?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
75
A $255,000 amount from an RRSP is used to purchase an annuity paying $6,000 at the end of each quarter. The annuity provides an annually compounded rate of return of 6%.
a) What will be the amount of the final payment?
b) What will be the interest portion of the 27th payment?
c) What will be the principal portion of the 53rd payment?
d) How much will the principal balance be reduced by Payments 14 to 20 inclusive?
e) How much interest will be paid by the payments received in the 6th year?
a) What will be the amount of the final payment?
b) What will be the interest portion of the 27th payment?
c) What will be the principal portion of the 53rd payment?
d) How much will the principal balance be reduced by Payments 14 to 20 inclusive?
e) How much interest will be paid by the payments received in the 6th year?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
76
$10,000 is to be repaid quarterly monthly over two years at 7.85% compounded semi-annually. Construct an amortization schedule for the loan. How much interest is paid in total?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
77
Monthly payments are required on a $45,000 loan at 6.0% compounded monthly. The loan has an amortization period of 15 years.
a) Calculate the interest component of Payment 137.
b) Calculate the principal component of Payment 76.
c) Calculate the interest paid in Year 1.
d) Calculate the interest paid in Year 1
a) Calculate the interest component of Payment 137.
b) Calculate the principal component of Payment 76.
c) Calculate the interest paid in Year 1.
d) Calculate the interest paid in Year 1

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
78
The interest rate for the first three years of an $163,000 mortgage is 5.4% compounded semi-annually. Monthly payments are based on a 20-year amortization. If a $4,000 prepayment is made at the end of the 16th month:
a) How much will the amortization period be shortened?
b) What will be the principal balance at the end of the three-year term?
a) How much will the amortization period be shortened?
b) What will be the principal balance at the end of the three-year term?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
79
A $350,000 mortgage is amortized over 25 years. What is the monthly payment if interest is 5.8% compounded quarterly?

Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck
80
A loan of $20,000 is to be repaid by equal semi-annual payments over three years at 7.5% compounded semi-annually. Construct an amortization schedule for the loan. How much interest is paid in total? 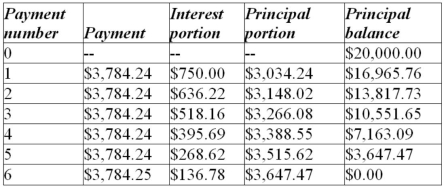


Unlock Deck
Unlock for access to all 188 flashcards in this deck.
Unlock Deck
k this deck


