Deck 6: Propositional Logic
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/354
Play
Full screen (f)
Deck 6: Propositional Logic
1
Thrifty's laying off workers is a sufficient condition for National's improving efficiency, if Enterprise reorganizes.
A) E ⊃ (N ⊃ T)
B) (T ⊃ N) ⊃ E
C) E ⊃ (T ⊃ N)
D) T ⊃ (N ⊃ E)
E) E ≡ (T ⊃ N)
A) E ⊃ (N ⊃ T)
B) (T ⊃ N) ⊃ E
C) E ⊃ (T ⊃ N)
D) T ⊃ (N ⊃ E)
E) E ≡ (T ⊃ N)
E ⊃ (T ⊃ N)
2
Statement 2I
Given the following statement:
(L • ∼ E) ≡ (E • ∼ L)
Statement 2I is:
A) Self-contradictory.
B) Tautologous.
C) Consistent.
D) Contingent.
E) Inconsistent.
Given the following statement:
(L • ∼ E) ≡ (E • ∼ L)
Statement 2I is:
A) Self-contradictory.
B) Tautologous.
C) Consistent.
D) Contingent.
E) Inconsistent.
Contingent.
3
In Proposition 2I, the main operator is a:
A) Tilde.
B) Wedge.
C) Horseshoe.
D) Triple bar.
E) Dot.
A) Tilde.
B) Wedge.
C) Horseshoe.
D) Triple bar.
E) Dot.
Triple bar.
4
If National's improving efficiency implies that Enterprise reorganizes, then Avis buys new cars.
A) (N ⊃ E ⊃ A)
B) N ⊃ (E ⊃ A)
C) (N ⊃ E) ⊃ A
D) A ⊃ (N ⊃ E)
E) (E ⊃ N) ⊃ A
A) (N ⊃ E ⊃ A)
B) N ⊃ (E ⊃ A)
C) (N ⊃ E) ⊃ A
D) A ⊃ (N ⊃ E)
E) (E ⊃ N) ⊃ A

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
5
In Proposition 1I, the main operator is a:
A) Dot.
B) Tilde.
C) Horseshoe.
D) Triple bar.
E) Wedge.
A) Dot.
B) Tilde.
C) Horseshoe.
D) Triple bar.
E) Wedge.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
6
The truth table for Statement 1I has how many lines?
A) Two.
B) Eight.
C) Four.
D) Six.
E) Nine.
A) Two.
B) Eight.
C) Four.
D) Six.
E) Nine.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
7
Statement 1I
Given the following statement:
(G • ∼ M) ⊃ (M ∨ G)
Statement 1I is:
A) Consistent.
B) Logically equivalent.
C) Tautologous.
D) Contingent.
E) Self-contradictory.
Given the following statement:
(G • ∼ M) ⊃ (M ∨ G)
Statement 1I is:
A) Consistent.
B) Logically equivalent.
C) Tautologous.
D) Contingent.
E) Self-contradictory.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
8
The truth table for Statement 3I has how many lines?
A) Six.
B) Nine.
C) Eleven.
D) Eight.
E) Four.
A) Six.
B) Nine.
C) Eleven.
D) Eight.
E) Four.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
9
Statement 3I
Given the following statement:
[K • (P ∨ ∼ R)] • [K ⊃ (R • ∼ P)]
Statement 3I is:
A) Valid.
B) Self-contradictory.
C) Tautologous.
D) Inconsistent.
E) Contingent.
Given the following statement:
[K • (P ∨ ∼ R)] • [K ⊃ (R • ∼ P)]
Statement 3I is:
A) Valid.
B) Self-contradictory.
C) Tautologous.
D) Inconsistent.
E) Contingent.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
10
Budget lowers rates unless Hertz and Thrifty do not overhaul operations.
A) B ∨ (∼H • ∼T)
B) B ∨ ∼(H • T)
C) B ⊃ (∼H • ∼T)
D) (∼H • ∼T) ⊃ B
E) (B ∨ ∼H) • ∼T
A) B ∨ (∼H • ∼T)
B) B ∨ ∼(H • T)
C) B ⊃ (∼H • ∼T)
D) (∼H • ∼T) ⊃ B
E) (B ∨ ∼H) • ∼T

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
11
Budget's lowering rates implies that Hertz runs a sale, only if Avis does not buy new cars.
A) (B ⊃ H) ⊃ ∼A
B) ∼A ⊃ (B ⊃ H)
C) (B ⊃ H) ≡ ∼A
D) (H ⊃ B) ⊃ ∼A
E) (B ⊃ H ⊃ A)
A) (B ⊃ H) ⊃ ∼A
B) ∼A ⊃ (B ⊃ H)
C) (B ⊃ H) ≡ ∼A
D) (H ⊃ B) ⊃ ∼A
E) (B ⊃ H ⊃ A)

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
12
Hertz's running a sale and Budget's lowering rates are a necessary condition for either Avis's buying new cars or Thrifty's laying off workers.
A) (A • T) ⊃ (H ∨ B)
B) (H • B) ⊃ (A ∨ T)
C) (H • B) ∨ (A ∨ T)
D) (A ∨ T) ⊃ (H • B)
E) (H • B) ≡ (A ∨ T)
A) (A • T) ⊃ (H ∨ B)
B) (H • B) ⊃ (A ∨ T)
C) (H • B) ∨ (A ∨ T)
D) (A ∨ T) ⊃ (H • B)
E) (H • B) ≡ (A ∨ T)

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
13
Proposition 1I
Given the following proposition:
[(B ≡ ∼ Y) • ∼(∼ X ⊃ A)] ∨ [∼(X ≡ A) ⊃ (Y • ∼ A)]
Given that A and B are true and X and Y are false, determine the truth value of Proposition 1I.
Given the following proposition:
[(B ≡ ∼ Y) • ∼(∼ X ⊃ A)] ∨ [∼(X ≡ A) ⊃ (Y • ∼ A)]
Given that A and B are true and X and Y are false, determine the truth value of Proposition 1I.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
14
National does not improve efficiency or Enterprise does not reorganize, given that Thrifty lays off workers.
A) T ⊃ ∼(N ∨ E)
B) (∼N ∨ ∼E) ⊃ T
C) ∼(N ∨ E) ⊃ T
D) (T ⊃ ∼N) ∨ ∼E
E) T ⊃ (∼N ∨ ∼E)
A) T ⊃ ∼(N ∨ E)
B) (∼N ∨ ∼E) ⊃ T
C) ∼(N ∨ E) ⊃ T
D) (T ⊃ ∼N) ∨ ∼E
E) T ⊃ (∼N ∨ ∼E)

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
15
Proposition 2I
Given the following proposition:
[∼(X ∨ B) ≡ (∼ Y ⊃ ∼ X)] ≡ ∼[(A ⊃ ∼ Y) • ∼(∼ X ⊃ ∼ B)]
Given that A and B are true and X and Y are false, determine the truth value of Proposition 2I.
Given the following proposition:
[∼(X ∨ B) ≡ (∼ Y ⊃ ∼ X)] ≡ ∼[(A ⊃ ∼ Y) • ∼(∼ X ⊃ ∼ B)]
Given that A and B are true and X and Y are false, determine the truth value of Proposition 2I.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
16
Given the pair of statements: R ∨ S and S ⊃ ∼ R
These statements are:
A) Inconsistent.
B) Contradictory.
C) Invalid.
D) Logically equivalent.
E) Consistent.
These statements are:
A) Inconsistent.
B) Contradictory.
C) Invalid.
D) Logically equivalent.
E) Consistent.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
17
Hertz runs a sale or both Avis buys new cars and Budget lowers rates.
A) H ∨ A • B
B) H ∨ (A • B)
C) (H ∨ A) • B
D) H • (A ∨ B)
E) H • A ∨ B
A) H ∨ A • B
B) H ∨ (A • B)
C) (H ∨ A) • B
D) H • (A ∨ B)
E) H • A ∨ B

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
18
Not both Hertz runs a sale and Thrifty lays off workers if either Avis buys new cars or Budget lowers rates.
A) (∼H • ∼T) ⊃ (A ∨ B)
B) (A ∨ B) ⊃ (∼H • ∼T)
C) ∼(H • T) ⊃ (A ∨ B)
D) (A ∨ B) ⊃ ∼(H • T)
E) (A • B) ⊃ ∼(H ∨ T)
A) (∼H • ∼T) ⊃ (A ∨ B)
B) (A ∨ B) ⊃ (∼H • ∼T)
C) ∼(H • T) ⊃ (A ∨ B)
D) (A ∨ B) ⊃ ∼(H • T)
E) (A • B) ⊃ ∼(H ∨ T)

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
19
National's improving efficiency or Enterprise's reorganizing is a sufficient and necessary condition for Thrifty's laying off workers, provided that Avis buys new cars.
A) (N ∨ E) ≡ (A ⊃ T)
B) A ⊃ [(N ∨ E) ≡ T]
C) [(N ∨ E) ≡ T] ⊃ A
D) A ⊃ [(N ⊃ E) • (E ⊃ N)]
E) A ≡ [(N ∨ E) ⊃ T]
A) (N ∨ E) ≡ (A ⊃ T)
B) A ⊃ [(N ∨ E) ≡ T]
C) [(N ∨ E) ≡ T] ⊃ A
D) A ⊃ [(N ⊃ E) • (E ⊃ N)]
E) A ≡ [(N ∨ E) ⊃ T]

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
20
Thrifty lays off workers only if neither National improves efficiency nor Enterprise reorganizes.
A) T ⊃ ∼(N ∨ E)
B) ∼(N ∨ E) ⊃ T
C) T ⊃ (∼N ∨ ∼T)
D) (∼N ∨ ∼E) ⊃ T
E) T ≡ ∼(N ∨ E)
A) T ⊃ ∼(N ∨ E)
B) ∼(N ∨ E) ⊃ T
C) T ⊃ (∼N ∨ ∼T)
D) (∼N ∨ ∼E) ⊃ T
E) T ≡ ∼(N ∨ E)

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
21
∼G ∨ ∼B 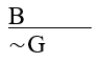
A) Disjunctive syllogism.
B) Invalid.
C) Denying the antecedent.
D) Affirming the consequent.
E) Modus tollens.
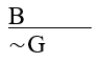
A) Disjunctive syllogism.
B) Invalid.
C) Denying the antecedent.
D) Affirming the consequent.
E) Modus tollens.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
22
S ⊃ ∼C 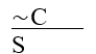
A) Modus tollens.
B) Affirming the consequent.
C) Denying the antecedent.
D) Modus ponens.
E) Invalid.
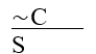
A) Modus tollens.
B) Affirming the consequent.
C) Denying the antecedent.
D) Modus ponens.
E) Invalid.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
23
Given the argument: S ⊃ E / N ⊃ (∼ S ⊃ E) // N ⊃ E
This argument is:
A) Invalid; fails in 5th line.
B) Invalid; fails in 6th line.
C) Valid.
D) Invalid; fails in 2nd line.
E) Invalid; fails in 3rd line.
This argument is:
A) Invalid; fails in 5th line.
B) Invalid; fails in 6th line.
C) Valid.
D) Invalid; fails in 2nd line.
E) Invalid; fails in 3rd line.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
24
In the expression 'P • Q', 'P' is called:
A) A conjunction.
B) A disjunct.
C) An antecedent.
D) A conjunct.
E) A disjunction.
A) A conjunction.
B) A disjunct.
C) An antecedent.
D) A conjunct.
E) A disjunction.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
25
E ⊃ ∼T 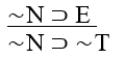
A) Modus ponens.
B) Constructive dilemma.
C) Pure hypothetical syllogism.
D) Invalid.
E) Disjunctive syllogism.
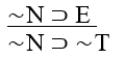
A) Modus ponens.
B) Constructive dilemma.
C) Pure hypothetical syllogism.
D) Invalid.
E) Disjunctive syllogism.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
26
∼Q ∨ S 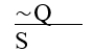
A) Disjunctive syllogism.
B) Modus ponens.
C) Invalid.
D) Modus tollens.
E) Denying the antecedent.
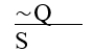
A) Disjunctive syllogism.
B) Modus ponens.
C) Invalid.
D) Modus tollens.
E) Denying the antecedent.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
27
Given the statements: W ⊃ (E ∨ ∼ G) / A ⊃ (G ∨ ∼ E) / H ⊃ (A • W) / H • E
These statements are:
A) Inconsistent.
B) Tautologous.
C) Invalid.
D) Logically equivalent.
E) Consistent.
These statements are:
A) Inconsistent.
B) Tautologous.
C) Invalid.
D) Logically equivalent.
E) Consistent.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
28
If a group of statements are consistent, this means:
A) At least one of them is true.
B) It is possible for all of them to be true.
C) At least one of them is false.
D) All of them are true.
E) It is possible for all of them to be false.
A) At least one of them is true.
B) It is possible for all of them to be true.
C) At least one of them is false.
D) All of them are true.
E) It is possible for all of them to be false.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
29
Given the argument: K ∨ B / K ≡ (D ∨ ∼ B) // K ⊃ D
This argument is:
A) Invalid; fails in 1st line.
B) Invalid; fails in 2nd line.
C) Valid.
D) Invalid; fails in 4th line.
E) Invalid; fails in 3rd line.
This argument is:
A) Invalid; fails in 1st line.
B) Invalid; fails in 2nd line.
C) Valid.
D) Invalid; fails in 4th line.
E) Invalid; fails in 3rd line.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
30
Given the statements: ∼ S ⊃ D / K ⊃ S / D ⊃ K / R ≡ ∼(S • C) / R ≡ C
These statements are:
A) Contradictory.
B) Tautologous.
C) Consistent.
D) Inconsistent.
E) Valid.
These statements are:
A) Contradictory.
B) Tautologous.
C) Consistent.
D) Inconsistent.
E) Valid.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
31
Given the argument: G ⊃ (N • E) / H ⊃ N / K ⊃ ∼E / (H • K) ≡ G
This argument is:
A) Valid.
B) Invalid.
C) Uncogent.
D) Cogent.
E) Sound.
This argument is:
A) Valid.
B) Invalid.
C) Uncogent.
D) Cogent.
E) Sound.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
32
(M ⊃ ∼T) • (∼H ⊃ T) 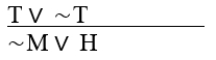
A) Invalid.
B) Destructive dilemma.
C) Constructive dilemma
D) Modus tollens.
E) Affirming the consequent.
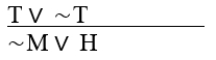
A) Invalid.
B) Destructive dilemma.
C) Constructive dilemma
D) Modus tollens.
E) Affirming the consequent.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
33
According to De Morgan's rule, ∼(P • Q) is logically equivalent to:
A) P ∨ Q
B) ∼P • ∼Q
C) ∼P ∨ ∼Q
D) P • Q
E) P ≡ Q
A) P ∨ Q
B) ∼P • ∼Q
C) ∼P ∨ ∼Q
D) P • Q
E) P ≡ Q

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
34
Given the argument: J ⊃ (E • Q) / ∼ Q ⊃ L / (E ∨ M) ⊃ (L ∨ ∼ Q) / M ∨ J // L
This argument is:
A) Valid.
B) Invalid.
C) Sound.
D) Cogent.
E) Uncogent.
This argument is:
A) Valid.
B) Invalid.
C) Sound.
D) Cogent.
E) Uncogent.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
35
Given the pair of statements: (H • J) ∨ (N • J) and (N ∨ H) ⊃ ∼ J
These statements are:
A) Contradictory.
B) Valid.
C) Logically equivalent.
D) Consistent.
E) Inconsistent.
These statements are:
A) Contradictory.
B) Valid.
C) Logically equivalent.
D) Consistent.
E) Inconsistent.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
36
(∼W ⊃ L) • (N ⊃ ∼R) 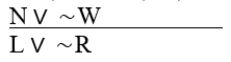
A) Invalid.
B) Pure hypothetical syllogism.
C) Destructive dilemma.
D) Denying the antecedent.
E) Constructive dilemma.
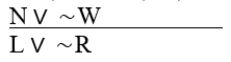
A) Invalid.
B) Pure hypothetical syllogism.
C) Destructive dilemma.
D) Denying the antecedent.
E) Constructive dilemma.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
37
K 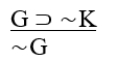
A) Disjunctive syllogism.
B) Invalid.
C) Denying the antecedent.
D) Modus tollens.
E) Affirming the consequent.
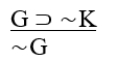
A) Disjunctive syllogism.
B) Invalid.
C) Denying the antecedent.
D) Modus tollens.
E) Affirming the consequent.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
38
F ⊃ ∼H 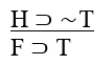
A) Pure hypothetical syllogism.
B) Constructive dilemma.
C) Invalid.
D) Affirming the consequent.
E) Disjunctive syllogism.
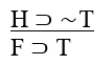
A) Pure hypothetical syllogism.
B) Constructive dilemma.
C) Invalid.
D) Affirming the consequent.
E) Disjunctive syllogism.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
39
R 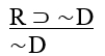
A) Invalid.
B) Affirming the consequent.
C) Disjunctive syllogism.
D) Modus tollens.
E) Modus ponens.
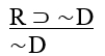
A) Invalid.
B) Affirming the consequent.
C) Disjunctive syllogism.
D) Modus tollens.
E) Modus ponens.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
40
∼F ⊃ L 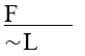
A) Denying the antecedent.
B) Modus ponens.
C) Affirming the consequent.
D) Modus tollens.
E) Invalid.
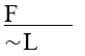
A) Denying the antecedent.
B) Modus ponens.
C) Affirming the consequent.
D) Modus tollens.
E) Invalid.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
41
Statement 1H
Given the following statement:
(S ⊃ ∼ R) ⊃ (∼ S • R)
The truth table for Statement 1H has how many lines?
A) Two.
B) Eight.
C) Four.
D) Six.
E) Nine.
Given the following statement:
(S ⊃ ∼ R) ⊃ (∼ S • R)
The truth table for Statement 1H has how many lines?
A) Two.
B) Eight.
C) Four.
D) Six.
E) Nine.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
42
Statement 1H
Given the following statement:
(S ⊃ ∼ R) ⊃ (∼ S • R)
Statement 1H is:
A) Consistent.
B) Logically equivalent.
C) Tautologous.
D) Contingent.
E) Self-contradictory.
Given the following statement:
(S ⊃ ∼ R) ⊃ (∼ S • R)
Statement 1H is:
A) Consistent.
B) Logically equivalent.
C) Tautologous.
D) Contingent.
E) Self-contradictory.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
43
Statement 2H
Given the following statement:
[N ∨ ∼ (K ∨ G)] ≡ [(G ⊃ N) • (K ⊃ N)]
Statement 2H is:
A) Inconsistent.
B) Contingent.
C) Consistent.
D) Self-contradictory.
E) Tautologous.
Given the following statement:
[N ∨ ∼ (K ∨ G)] ≡ [(G ⊃ N) • (K ⊃ N)]
Statement 2H is:
A) Inconsistent.
B) Contingent.
C) Consistent.
D) Self-contradictory.
E) Tautologous.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
44
United's lowering fares is a sufficient and necessary condition for American's hiring pilots, given that Frontier does not improve service.
A) (U ≡ A) ⊃ ∼F
B) ∼F ⊃ (U ≡ A)
C) (∼F ⊃ U) • (∼F ⊃ A)
D) (∼F ≡ U) • (∼F ≡ A)
E) ∼F ≡ (U ⊃ A)
A) (U ≡ A) ⊃ ∼F
B) ∼F ⊃ (U ≡ A)
C) (∼F ⊃ U) • (∼F ⊃ A)
D) (∼F ≡ U) • (∼F ≡ A)
E) ∼F ≡ (U ⊃ A)

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
45
Proposition 2H
Given the following proposition:
∼[(B • ∼X) ⊃ ∼(Y ≡ ∼B)] ⊃ [∼(X ⊃ A) ∨ (B ⊃ ∼Y)]
Given that A and B are true and X and Y are false, determine the truth value of Proposition 2H.
Given the following proposition:
∼[(B • ∼X) ⊃ ∼(Y ≡ ∼B)] ⊃ [∼(X ⊃ A) ∨ (B ⊃ ∼Y)]
Given that A and B are true and X and Y are false, determine the truth value of Proposition 2H.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
46
The wedge operator is used to translate:
A) "Nevertheless."
B) "Moreover."
C) "Unless."
D) "Implies."
E) "Provided that."
A) "Nevertheless."
B) "Moreover."
C) "Unless."
D) "Implies."
E) "Provided that."

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
47
Frontier's improving service is a necessary condition for either JetBlue's buying planes or United's lowering fares.
A) F ≡ (J ∨ U)
B) F ⊃ (J ∨ U)
C) (F ⊃ J) • (F ⊃ U)
D) (J ∨ U) ⊃ F
E) (J ⊃F) ∨ (F ⊃ U)
A) F ≡ (J ∨ U)
B) F ⊃ (J ∨ U)
C) (F ⊃ J) • (F ⊃ U)
D) (J ∨ U) ⊃ F
E) (J ⊃F) ∨ (F ⊃ U)

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
48
American's hiring pilots is a sufficient condition for both Delta's advertising a sale and Southwest's expanding routes.
A) (D • S) ∨ A
B) (D ⊃ A) • (S ⊃ A)
C) (D • S) ⊃ A
D) A ⊃ (D • S)
E) A ≡ (D • S)
A) (D • S) ∨ A
B) (D ⊃ A) • (S ⊃ A)
C) (D • S) ⊃ A
D) A ⊃ (D • S)
E) A ≡ (D • S)

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
49
Proposition 1H
Given the following proposition:
[(A ≡ ∼B) ∨ (X ⊃ Y)] • [(Y ⊃ A) ≡ ∼(X ∨ B)]
In Proposition 1H, the main operator is a:
A) Horseshoe.
B) Tilde.
C) Dot.
D) Triple bar.
E) Wedge.
Given the following proposition:
[(A ≡ ∼B) ∨ (X ⊃ Y)] • [(Y ⊃ A) ≡ ∼(X ∨ B)]
In Proposition 1H, the main operator is a:
A) Horseshoe.
B) Tilde.
C) Dot.
D) Triple bar.
E) Wedge.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
50
Frontier's improving service implies that not both JetBlue buys planes and Southwest expands routes.
A) F ⊃ ∼(J ∨ S)
B) F ⊃ (∼J • ∼S)
C) F ⊃ ∼(J • S)
D) (F ⊃ ∼J) • S
E) F ≡ ∼(J • S)
A) F ⊃ ∼(J ∨ S)
B) F ⊃ (∼J • ∼S)
C) F ⊃ ∼(J • S)
D) (F ⊃ ∼J) • S
E) F ≡ ∼(J • S)

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
51
If an indirect truth table requiring more than one line is constructed for either an argument or a series of statements and a contradiction is derived on the first line, then:
A) The second line must be completed.
B) The argument is valid and the statements are consistent.
C) The argument is valid and the statements are inconsistent.
D) The argument is invalid and the statements are consistent.
E) The argument is invalid and the statements are inconsistent.
A) The second line must be completed.
B) The argument is valid and the statements are consistent.
C) The argument is valid and the statements are inconsistent.
D) The argument is invalid and the statements are consistent.
E) The argument is invalid and the statements are inconsistent.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
52
Proposition 2H
Given the following proposition:
∼[(B • ∼X) ⊃ ∼(Y ≡ ∼B)] ⊃ [∼(X ⊃ A) ∨ (B ⊃ ∼Y)]
In Proposition 2H, the main operator is a:
A) Dot.
B) Wedge.
C) Triple bar.
D) Tilde.
E) Horseshoe.
Given the following proposition:
∼[(B • ∼X) ⊃ ∼(Y ≡ ∼B)] ⊃ [∼(X ⊃ A) ∨ (B ⊃ ∼Y)]
In Proposition 2H, the main operator is a:
A) Dot.
B) Wedge.
C) Triple bar.
D) Tilde.
E) Horseshoe.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
53
JetBlue buys planes if and only if both Delta does not advertise a sale and Southwest does not expand routes.
A) J ≡ ∼(D • S)
B) J ⊃ (∼D • ∼S)
C) J ≡ (∼D • ∼S)
D) ∼(D ∨ S) ⊃ J
E) J ∨ (∼D • ∼S)
A) J ≡ ∼(D • S)
B) J ⊃ (∼D • ∼S)
C) J ≡ (∼D • ∼S)
D) ∼(D ∨ S) ⊃ J
E) J ∨ (∼D • ∼S)

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
54
Delta advertises a sale and either United lowers fares or American hires pilots.
A) D • (U ∨ A)
B) D ∨ (U • A)
C) D • U ∨ A
D) (D • U) ∨ A
E) D ∨ (U • A).
A) D • (U ∨ A)
B) D ∨ (U • A)
C) D • U ∨ A
D) (D • U) ∨ A
E) D ∨ (U • A).

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
55
Statement 2H
Given the following statement:
[N ∨ ∼ (K ∨ G)] ≡ [(G ⊃ N) • (K ⊃ N)]
The truth table for Statement 2H has how many lines?
A) Five.
B) Nine.
C) Eight.
D) Six.
E) Four.
Given the following statement:
[N ∨ ∼ (K ∨ G)] ≡ [(G ⊃ N) • (K ⊃ N)]
The truth table for Statement 2H has how many lines?
A) Five.
B) Nine.
C) Eight.
D) Six.
E) Four.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
56
Southwest expands routes if either American does not hire pilots or United does not lower fares.
A) ∼(A ∨ U) ⊃ S
B) (∼A • ∼U) ⊃ S
C) S ⊃ (∼A ∨ ∼U)
D) (S ⊃ ∼A ∨ ∼U)
E) (∼A ∨ ∼U) ⊃ S
A) ∼(A ∨ U) ⊃ S
B) (∼A • ∼U) ⊃ S
C) S ⊃ (∼A ∨ ∼U)
D) (S ⊃ ∼A ∨ ∼U)
E) (∼A ∨ ∼U) ⊃ S

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
57
Proposition 1H
Given the following proposition:
[(A ≡ ∼B) ∨ (X ⊃ Y)] • [(Y ⊃ A) ≡ ∼(X ∨ B)]
Given that A and B are true and X and Y are false, determine the truth value of Proposition 1H.
Given the following proposition:
[(A ≡ ∼B) ∨ (X ⊃ Y)] • [(Y ⊃ A) ≡ ∼(X ∨ B)]
Given that A and B are true and X and Y are false, determine the truth value of Proposition 1H.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
58
United lowers fares if and only if both JetBlue buys planes and Delta advertises a sale, provided that American hires pilots.
A) (U ≡ A) • (J ≡ D)
B) A ⊃ [U ≡ (J • D)]
C) [U ≡ (J • D)] ⊃ A
D) A ⊃ [(U ⊃ J) • (D ⊃ U]
E) [U ⊃ (J • D)] ⊃ A
A) (U ≡ A) • (J ≡ D)
B) A ⊃ [U ≡ (J • D)]
C) [U ≡ (J • D)] ⊃ A
D) A ⊃ [(U ⊃ J) • (D ⊃ U]
E) [U ⊃ (J • D)] ⊃ A

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
59
JetBlue buys planes if Delta advertises a sale, and Frontier improves service only if Southwest expands routes.
A) (D ⊃ J) • (F ⊃ S)
B) (D ≡ J) • (F ≡ S)
C) (J ⊃ D) • (S ⊃ F)
D) (D • J) ⊃ (S • F)
E) (J ⊃ D) • (F ⊃ S)
A) (D ⊃ J) • (F ⊃ S)
B) (D ≡ J) • (F ≡ S)
C) (J ⊃ D) • (S ⊃ F)
D) (D • J) ⊃ (S • F)
E) (J ⊃ D) • (F ⊃ S)

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
60
JetBlue buys planes unless neither Frontier improves service nor United lowers fares.
A) J ∨ ∼(F • U)
B) J ∨ ∼(F ∨ U)
C) J ∨ (∼F ∨ ∼U)
D) J ⊃ ∼(F ∨ U)
E) ∼(F ∨ U) ⊃ J
A) J ∨ ∼(F • U)
B) J ∨ ∼(F ∨ U)
C) J ∨ (∼F ∨ ∼U)
D) J ⊃ ∼(F ∨ U)
E) ∼(F ∨ U) ⊃ J

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
61
(K ⊃ ∼A) • (S ⊃ ∼D) 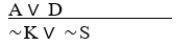
A) Invalid.
B) Modus tollens.
C) Affirming the consequent.
D) Denying the antecedent.
E) Destructive dilemma.
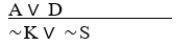
A) Invalid.
B) Modus tollens.
C) Affirming the consequent.
D) Denying the antecedent.
E) Destructive dilemma.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
62
Given the statement: (E ∨ ∼ H) • (H • ∼ E)
This statement is:
A) Valid.
B) Self-contradictory.
C) Tautologous.
D) Inconsistent.
E) Contingent.
This statement is:
A) Valid.
B) Self-contradictory.
C) Tautologous.
D) Inconsistent.
E) Contingent.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
63
(∼N ⊃ R) • (F ⊃ ∼G) 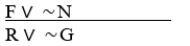
A) Constructive dilemma.
B) Invalid.
C) Denying the antecedent.
D) Modus tollens.
E) Destructive dilemma.

A) Constructive dilemma.
B) Invalid.
C) Denying the antecedent.
D) Modus tollens.
E) Destructive dilemma.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
64
B ⊃ ∼Q Q
∼B
A) Modus ponens.
B) Modus tollens.
C) Disjunctive syllogism.
D) Invalid.
E) Denying the antecedent.
∼B
A) Modus ponens.
B) Modus tollens.
C) Disjunctive syllogism.
D) Invalid.
E) Denying the antecedent.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
65
Given the argument: M ⊃ J / ∼ J ⊃ R // (M ∨ ∼ R) ⊃ J
This argument is:
A) Invalid; fails in 3rd line.
B) Invalid; fails in 2nd line.
C) Invalid; fails in 4th line.
D) Invalid; fails in 1st line.
E) Valid.
This argument is:
A) Invalid; fails in 3rd line.
B) Invalid; fails in 2nd line.
C) Invalid; fails in 4th line.
D) Invalid; fails in 1st line.
E) Valid.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
66
D ⊃ ∼N 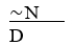
A) Affirming the consequent.
B) Invalid.
C) Denying the antecedent.
D) Modus ponens.
E) Modus tollens.
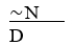
A) Affirming the consequent.
B) Invalid.
C) Denying the antecedent.
D) Modus ponens.
E) Modus tollens.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
67
∼P ∨ M 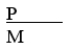
A) Modus tollens.
B) Denying the antecedent.
C) Pure hypothetical syllogism.
D) Disjunctive syllogism.
E) Invalid.
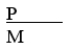
A) Modus tollens.
B) Denying the antecedent.
C) Pure hypothetical syllogism.
D) Disjunctive syllogism.
E) Invalid.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
68
Given the statements: H ⊃ E / M ⊃ R / (M • E) ⊃ G / (R • G) ⊃ E / M ∨ E
These statements are:
A) Invalid.
B) Tautologous.
C) Consistent.
D) Logically equivalent.
E) Inconsistent.
These statements are:
A) Invalid.
B) Tautologous.
C) Consistent.
D) Logically equivalent.
E) Inconsistent.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
69
Given the pair of statements: G ⊃ (W • ∼ Q) and (W ∨ ∼ G) • ∼(Q • G)
These statements are:
A) Inconsistent.
B) Contradictory.
C) Invalid.
D) Logically equivalent.
E) Consistent.
These statements are:
A) Inconsistent.
B) Contradictory.
C) Invalid.
D) Logically equivalent.
E) Consistent.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
70
In the expression 'P ∨ Q', 'P' is called:
A) A disjunction.
B) A conjunct.
C) A disjunct.
D) A conjunction.
E) An antecedent.
A) A disjunction.
B) A conjunct.
C) A disjunct.
D) A conjunction.
E) An antecedent.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
71
Given the statements: C ⊃ L / K ⊃ ∼H / L ⊃ (N ⊃ K) / C ⊃ (H ⊃ N) / C • H
These statements are:
A) Contradictory.
B) Tautologous.
C) Consistent.
D) Inconsistent.
E) Valid.
These statements are:
A) Contradictory.
B) Tautologous.
C) Consistent.
D) Inconsistent.
E) Valid.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
72
Given the argument: R ⊃ (H • ∼N) / (H • ∼B) ⊃ (N ∨ ∼P) / K ⊃ (G • P) // (K • R) ⊃ B
This argument is:
A) Invalid.
B) Valid.
C) Uncogent.
D) Cogent.
E) Sound.
This argument is:
A) Invalid.
B) Valid.
C) Uncogent.
D) Cogent.
E) Sound.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
73
∼H ⊃ ∼B 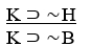
A) Denying the antecedent.
B) Invalid.
C) Pure hypothetical syllogism.
D) Constructive dilemma.
E) Destructive dilemma.
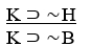
A) Denying the antecedent.
B) Invalid.
C) Pure hypothetical syllogism.
D) Constructive dilemma.
E) Destructive dilemma.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
74
Given the argument: S ⊃ W / C ⊃ L / (M • ∼L) ∨ (D • ∼W) / C ∨ S // D • M
This argument is:
A) Invalid.
B) Cogent.
C) Sound.
D) Valid.
E) Uncogent.
This argument is:
A) Invalid.
B) Cogent.
C) Sound.
D) Valid.
E) Uncogent.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
75
∼L ⊃ F 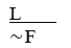
A) Disjunctive syllogism.
B) Denying the antecedent.
C) Modus tollens.
D) Modus ponens.
E) Invalid.
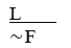
A) Disjunctive syllogism.
B) Denying the antecedent.
C) Modus tollens.
D) Modus ponens.
E) Invalid.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
76
Given the argument: Q ⊃ A / ∼ (A • Q) / A ≡ Q
This argument is:
A) Invalid; fails in 1st line.
B) Valid.
C) Invalid; fails in 3rd line.
D) Invalid; fails in 2nd line.
E) Invalid; fails in 4th line.
This argument is:
A) Invalid; fails in 1st line.
B) Valid.
C) Invalid; fails in 3rd line.
D) Invalid; fails in 2nd line.
E) Invalid; fails in 4th line.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
77
Given the pair of statements: P • ∼ Z and Z ≡ P
These statements are:
A) Inconsistent.
B) Valid.
C) Contradictory.
D) Consistent.
E) Logically equivalent.
These statements are:
A) Inconsistent.
B) Valid.
C) Contradictory.
D) Consistent.
E) Logically equivalent.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
78
S ⊃ ∼R 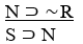
A) Disjunctive syllogism.
B) Constructive dilemma.
C) Pure hypothetical syllogism.
D) Affirming the consequent.
E) Invalid.
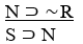
A) Disjunctive syllogism.
B) Constructive dilemma.
C) Pure hypothetical syllogism.
D) Affirming the consequent.
E) Invalid.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
79
G ∨ ∼T 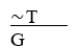
A) Invalid.
B) Disjunctive syllogism.
C) Modus ponens.
D) Affirming the consequent.
E) Modus tollens.
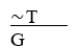
A) Invalid.
B) Disjunctive syllogism.
C) Modus ponens.
D) Affirming the consequent.
E) Modus tollens.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck
80
∼G 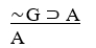
A) Constructive dilemma.
B) Disjunctive syllogism.
C) Modus ponens.
D) Denying the antecedent.
E) Invalid.
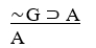
A) Constructive dilemma.
B) Disjunctive syllogism.
C) Modus ponens.
D) Denying the antecedent.
E) Invalid.

Unlock Deck
Unlock for access to all 354 flashcards in this deck.
Unlock Deck
k this deck


