Deck 7: Applications of Trigonometry
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/86
Play
Full screen (f)
Deck 7: Applications of Trigonometry
1
Use the following to answer questions :
A radar ship is 25.0 miles off shore from a major port when a large fleet of ships leaves the port at the 40.0° angle shown.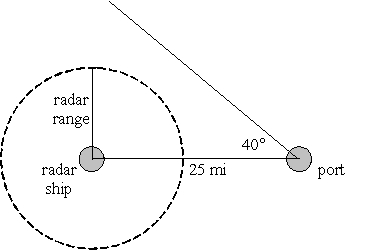
If the maximum range of the ship's radar is 16.0 miles, will the departing fleet be detected?
A) yes
B) no
A radar ship is 25.0 miles off shore from a major port when a large fleet of ships leaves the port at the 40.0° angle shown.

If the maximum range of the ship's radar is 16.0 miles, will the departing fleet be detected?
A) yes
B) no
no
2
Use the following to answer questions :
In A = 60°, and side c = 26 ft.
A = 60°, and side c = 26 ft.
-How many triangles can be formed if side a = 10 ft?
A) 0
B) 1
C) 2
D) 3
In
 A = 60°, and side c = 26 ft.
A = 60°, and side c = 26 ft.-How many triangles can be formed if side a = 10 ft?
A) 0
B) 1
C) 2
D) 3
0
3
Use the following to answer questions :
In A = 60°, and side c = 26 ft.
A = 60°, and side c = 26 ft.
-How many triangles can be formed if side a = 23 ft?
A) 0
B) 1
C) 2
D) 3
In
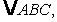 A = 60°, and side c = 26 ft.
A = 60°, and side c = 26 ft.-How many triangles can be formed if side a = 23 ft?
A) 0
B) 1
C) 2
D) 3
1
4
Solve using the law of sines and a scaled drawing. Round to the nearest tenth. If two triangles exist, solve both completely.
side c = 27.5 mi
A = 44°
side a = 10.1 mi
side c = 27.5 mi
A = 44°
side a = 10.1 mi

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
5
Solve using the law of sines and a scaled drawing. If two triangles exist, solve both completely.
side a = 23.6 yd
A = 30°
side c = 47.2 yd
side a = 23.6 yd
A = 30°
side c = 47.2 yd

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
6
Solve the triangle using the law of sines. If the law of sines cannot be used, state why. Round sides to the nearest tenth. 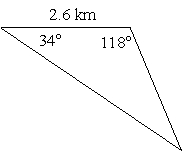


Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
7
Assume the law of sines is being applied to solve a triangle. Solve for A (if possible), then determine if a second angle (0° < < 180°) exists that also satisfies the proportion. Round to the nearest tenth of a degree. 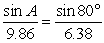
A) 41.1°
B) 41.1°, 138.9°
C) 41.7°, 138.3°
D) not possible
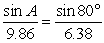
A) 41.1°
B) 41.1°, 138.9°
C) 41.7°, 138.3°
D) not possible

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
8
Determine the length to the nearest tenth of a foot of both rafters in the diagram. 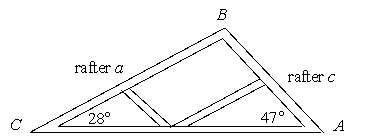 42 feet
42 feet
 42 feet
42 feet
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
9
Solve the following equation for a. Round to the nearest hundredth. 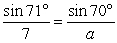
A) a 6.01
B) a 6.96
C) a 7.67
D) a 8.09
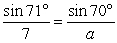
A) a 6.01
B) a 6.96
C) a 7.67
D) a 8.09

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
10
Use the following to answer questions :
In A = 60°, and side c = 26 ft.
A = 60°, and side c = 26 ft.
-How many triangles can be formed if side a = 17 ft?
A) 0
B) 1
C) 2
D) 3
In
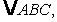 A = 60°, and side c = 26 ft.
A = 60°, and side c = 26 ft.-How many triangles can be formed if side a = 17 ft?
A) 0
B) 1
C) 2
D) 3

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
11
Use the following to answer questions :
A radar ship is 25.0 miles off shore from a major port when a large fleet of ships leaves the port at the 40.0° angle shown.
-If the maximum range of the ship's radar is 18 miles, approximately how far from port (to the nearest tenth of a mile) is the fleet when it is first detected?
A). 11.0 mi
B). 14.6 mi
C). 23.9 mi
D). 27.3 mi
A radar ship is 25.0 miles off shore from a major port when a large fleet of ships leaves the port at the 40.0° angle shown.

-If the maximum range of the ship's radar is 18 miles, approximately how far from port (to the nearest tenth of a mile) is the fleet when it is first detected?
A). 11.0 mi
B). 14.6 mi
C). 23.9 mi
D). 27.3 mi

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
12
Determine whether the law of cosines can be used to begin the solution process for the triangle. 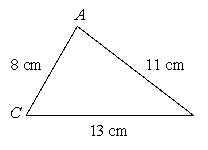
A) yes
B) no

A) yes
B) no

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
13
Assume the law of sines is being applied to solve a triangle. Solve for B (if possible), then determine if a second angle (0° < < 180°) exists that also satisfies the proportion. Round to the nearest tenth of a degree. 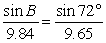
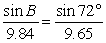

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
14
Use the following to answer questions :
In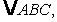 A = 60°, and side c = 26 ft.
A = 60°, and side c = 26 ft.
-Assuming that side c is the longest side, what length for side a will produce a right triangle?
A) 11 ft
B)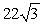 ft
ft
C)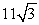 ft
ft
D) 44 ft
In
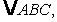 A = 60°, and side c = 26 ft.
A = 60°, and side c = 26 ft.-Assuming that side c is the longest side, what length for side a will produce a right triangle?
A) 11 ft
B)
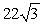 ft
ftC)
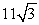 ft
ftD) 44 ft

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
15
Determine whether the law of cosines can be used to begin the solution process for the triangle. 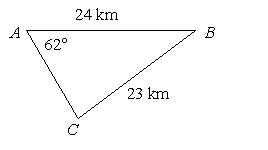
A) yes
B) no

A) yes
B) no

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
16
Solve the triangle using the law of sines. If the law of sines cannot be used, state why. Round sides to the nearest tenth.
B = 21°
side a = 18 yd
C = 84°
B = 21°
side a = 18 yd
C = 84°

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
17
Solve using the law of sines and a scaled drawing. Round to the nearest tenth. If two triangles exist, solve both completely.
side c = 25.0 ft
C = 62°
side b = 26.3 ft
side c = 25.0 ft
C = 62°
side b = 26.3 ft

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
18
Solve using the law of sines and a scaled drawing. Round to the nearest tenth. If two triangles exist, solve both completely. side b = 20.0 mi
B = 51°
Side a = 21.6 mi
A) A 57.1°, C 71.9°
C 24.5 mi
B) A 122.9° C 6.1°
C 2.7 mi
C) A 57.1° C 71.9°
C 24.5 mi
Or
A 122.9°
C 6.1°
C 2.7 mi
D) not possible
B = 51°
Side a = 21.6 mi
A) A 57.1°, C 71.9°
C 24.5 mi
B) A 122.9° C 6.1°
C 2.7 mi
C) A 57.1° C 71.9°
C 24.5 mi
Or
A 122.9°
C 6.1°
C 2.7 mi
D) not possible

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
19
Solve for B (0 < B < 90°), if possible. Round to the nearest tenth of a degree. 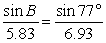
A) 53.6°
B) 54.4°
C) 55.1°
D) not possible
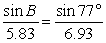
A) 53.6°
B) 54.4°
C) 55.1°
D) not possible

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
20
Solve the triangle using the law of sines. Round sides to the nearest tenth. side a = 5 m
A = 56°
B = 41°
A). C = 83° b 3.3 m
C 5.4 m
B). C = 83° b 3.8 m
C 6.4 m
C). C = 83° b 4.0 m
C 6.0 m
D). C = 83° b 4.5 m
C 5.8 m
A = 56°
B = 41°
A). C = 83° b 3.3 m
C 5.4 m
B). C = 83° b 3.8 m
C 6.4 m
C). C = 83° b 4.0 m
C 6.0 m
D). C = 83° b 4.5 m
C 5.8 m

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
21
The magnitude of vector v is given, along with the quadrant of the terminal point and the angle it makes with the nearest x-axis. Find the horizontal and vertical components of v and write the results in component form. Round to one decimal place. |v| = 17; = 78°; QIII
A) v =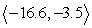
B) v =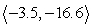
C) v =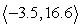
D) v =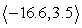
A) v =
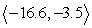
B) v =
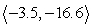
C) v =
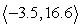
D) v =
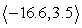

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
22
Solve the triangle using the law of cosines. Round to tenths. 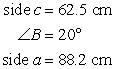
A) A 22.0° C 138.0°
B 80.7 cm
B) A 158.0° C 2.0°
B 80.7 cm
C) A 56.0° C 104.0°
B 36.4 cm
D) A 124.0° C 36.0°
B 36.4 cm
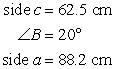
A) A 22.0° C 138.0°
B 80.7 cm
B) A 158.0° C 2.0°
B 80.7 cm
C) A 56.0° C 104.0°
B 36.4 cm
D) A 124.0° C 36.0°
B 36.4 cm

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
23
Use the following to answer questions :
u =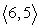 ; v =
; v = 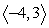
Compute u - v.
A)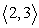
B)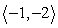
C)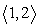
D)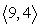
u =
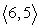 ; v =
; v = 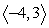
Compute u - v.
A)
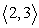
B)
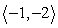
C)
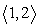
D)
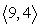

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
24
Use the following to answer questions :
v =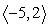
Graph the vector.
v =
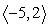
Graph the vector.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
25
Determine whether the law of cosines can be used to begin the solution process for the triangle. 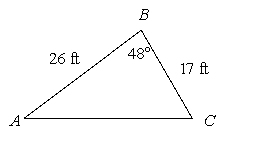
A) yes
B) no

A) yes
B) no

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
26
Two tractors are pulling at a stump in an effort to clear land for more crops. The Massey-Ferguson is pulling with a force of 200 N, while the John Deere is pulling with a force of 250 N. The chains attached to the stump and each tractor form a 28° angle. Represent this situation using geometric vectors.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
27
u = 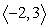 ; v =
; v = 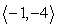 (a) Compute u + v.
(a) Compute u + v.
(b) Illustrate u + v graphically.
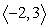 ; v =
; v = 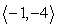 (a) Compute u + v.
(a) Compute u + v.(b) Illustrate u + v graphically.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
28
Use the following to answer questions :
u =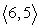 ; v =
; v = 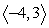
Compute u + v.
A)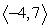
B)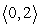
C)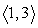
D)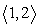
u =
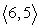 ; v =
; v = 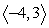
Compute u + v.
A)
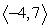
B)
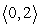
C)
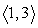
D)
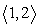

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
29
Use the following to answer questions :
Vector v =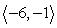 has initial point (2, 5).
has initial point (2, 5).
Find the coordinates of the terminal point of the vector.
A) (-7, 9)
B) (1, 7)
C) (-1, -7)
D) (-7, 7)
Vector v =
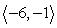 has initial point (2, 5).
has initial point (2, 5).Find the coordinates of the terminal point of the vector.
A) (-7, 9)
B) (1, 7)
C) (-1, -7)
D) (-7, 7)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
30
Determine whether the law of cosines can be used to begin the solution process for the triangle. 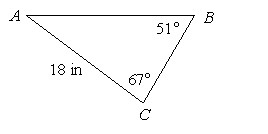
A) yes
B) no

A) yes
B) no

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
31
Two planes leave an airport at the same time. One travels due west (bearing 270°) with a cruising speed of 420 mph. The other travels at bearing 235° with a cruising speed of 440 mph. Approximate the distance between the planes after 3 hours of flight.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
32
A pilot wishes to fly from Pleasant Hills to Sheldon. She calculates the distances shown using a map, with York for reference since it is due east from Pleasant Hills. What heading should she set for this trip (i.e., what is the measure of angle P)? 91 miles 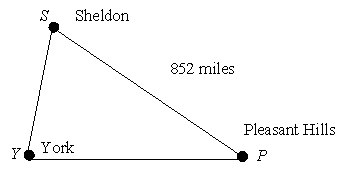 790 miles
790 miles
A) 3.8°
B) 4.7°
C) 5.9°
D) 6.6°
 790 miles
790 milesA) 3.8°
B) 4.7°
C) 5.9°
D) 6.6°

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
33
Solve using the law of cosines (if possible). Round to tenths.
side a = 153 yd
side b = 168 yd
side c = 103 yd
side a = 153 yd
side b = 168 yd
side c = 103 yd

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
34
Use the following to answer questions :
v =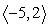
-Find the acute angle formed by the vector and the nearest x-axis. Round to the nearest tenth of a degree.
v =
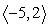
-Find the acute angle formed by the vector and the nearest x-axis. Round to the nearest tenth of a degree.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
35
Use the following to answer questions :
v =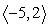
Compute the magnitude of the vector exactly.
v =
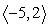
Compute the magnitude of the vector exactly.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
36
Vector v1 is a geometric vector representing a car traveling at 15 mph. Vectors v2, v3, and v4 are vectors representing cars traveling at 10 mph, 20 mph, and 5 mph respectively. Draw these vectors given that v4 is traveling the same direction and parallel to v1, while v2 and v3 are traveling in the opposite direction and parallel to v1.
A)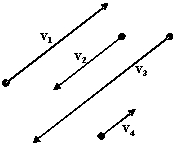
B)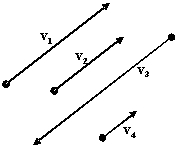
C)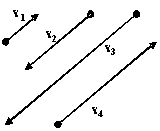
D)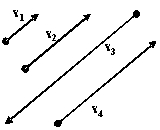
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
37
Solve the triangle using the law of cosines. Round to tenths. 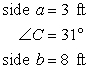
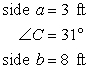

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
38
Solve for the unknown part.. Round to one decimal place. b2 = (7)2 + (6)2 - 2(7)(6)cos(67°)
A) b = 7.2
B) b = 8.0
C) b = 8.6
D) b = 9.4
A) b = 7.2
B) b = 8.0
C) b = 8.6
D) b = 9.4

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
39
Solve for the unknown part. Round to one decimal place. 52 = (9)2 + (10)2 - 2(9)(10)cos(A)
A) A 29.4°
B) A 29.6°
C) A 29.9°
D) A 30.2°
A) A 29.4°
B) A 29.6°
C) A 29.9°
D) A 30.2°

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
40
Use the following to answer questions :
Vector v =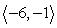 has initial point (2, 5).
has initial point (2, 5).
Find the magnitude |v| of the vector.
A) 13
B) 37
C)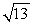
D)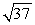
Vector v =
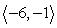 has initial point (2, 5).
has initial point (2, 5).Find the magnitude |v| of the vector.
A) 13
B) 37
C)
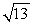
D)
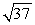

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
41
Find the amount of work required to move an object along the entire length of v with force F. Assume force is in pounds and distance is in feet.
F =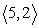 ; v =
; v = 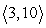
F =
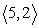 ; v =
; v = 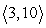

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
42
Hal pushes a box full of books 40 ft. If he uses a constant force of 75 pounds, how much work did he do?

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
43
Find a unit vector pointing in the same direction as the vector v = -2i - 5j.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
44
Use the following to answer questions :
u =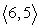 ; v =
; v = 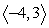
Compute 4u + 5v.
A)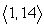
B)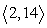
C)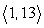
D)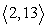
u =
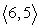 ; v =
; v = 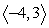
Compute 4u + 5v.
A)
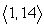
B)
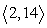
C)
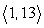
D)
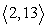

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
45
Use the following to answer questions :
p =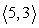 ; q =
; q = 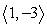
Find the angle between the vectors to the nearest tenth of a degree.
A) 165.5°
B) 166.3°
C) 166.7°
D) 168.0°
p =
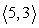 ; q =
; q = 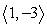
Find the angle between the vectors to the nearest tenth of a degree.
A) 165.5°
B) 166.3°
C) 166.7°
D) 168.0°

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
46
Use the following to answer questions :
p =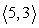 ; q =
; q = 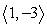
Compute the dot product p • q.
A)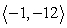
B)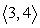
C) -13
D) 11
p =
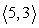 ; q =
; q = 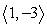
Compute the dot product p • q.
A)
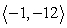
B)
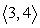
C) -13
D) 11

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
47
Find the component of u along v (compute compvu) for the vectors u and v given. Round to the nearest hundredth. 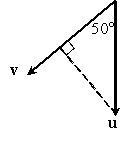 1475 lbs
1475 lbs
 1475 lbs
1475 lbs
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
48
Find a unit vector pointing in the same direction as the vector v = 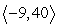 .
.
A)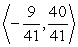
B)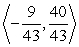
C)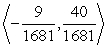
D)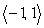
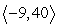 .
.A)
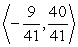
B)
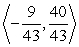
C)
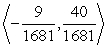
D)
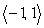

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
49
Use the following to answer questions :
u = -2i + j; v = 4i + 3j
Compute u + v.
A) i + j
B) 9i - 7j
C) 9i - 6j
D) 8i - 7j
u = -2i + j; v = 4i + 3j
Compute u + v.
A) i + j
B) 9i - 7j
C) 9i - 6j
D) 8i - 7j

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
50
Find the component of u along v (compute compvu) for the vectors u and v given. Round to the nearest hundredth. 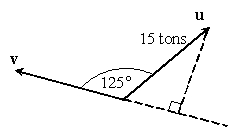
A) 8.60 tons
B) -8.60 tons
C) 12.29 tons
D) -12.29 tons

A) 8.60 tons
B) -8.60 tons
C) 12.29 tons
D) -12.29 tons

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
51
An arrow is shot into the air at an angle of 66° with an initial velocity of 18 ft/sec. Compute the horizontal and vertical components of the representative vector. Round to the nearest tenth.
A) Horizontal component: 7.8 ft/sec; Vertical component: 15.9 ft/sec
B) Horizontal component: 15.9 ft/sec; Vertical component: 7.8 ft/sec
C) Horizontal component: 16.4 ft/sec; Vertical component: 7.3 ft/sec
D) Horizontal component: 7.3 ft/sec; Vertical component: 16.4 ft/sec
A) Horizontal component: 7.8 ft/sec; Vertical component: 15.9 ft/sec
B) Horizontal component: 15.9 ft/sec; Vertical component: 7.8 ft/sec
C) Horizontal component: 16.4 ft/sec; Vertical component: 7.3 ft/sec
D) Horizontal component: 7.3 ft/sec; Vertical component: 16.4 ft/sec

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
52
A baby-sitter pulls some kids in a wagon on a level street. How much work is done if she pulls the wagon 200 feet at a constant force of 45 lbs with the wagon handle making an angle of 34° with the street? Round to the nearest whole number.
A) approximately 4808 ft-lbs
B) approximately 5033 ft-lbs
C) approximately 6529 ft-lbs
D) approximately 7461 ft-lbs
A) approximately 4808 ft-lbs
B) approximately 5033 ft-lbs
C) approximately 6529 ft-lbs
D) approximately 7461 ft-lbs

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
53
The force vectors F1 = -5i + j and F2 = -4i - 5j are acting on a common point P. Find an additional force vector so that equilibrium takes place.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
54
For the vector below, represents the acute angle formed by the vector and the x-axis. Write the vector in i, j form. Round to the nearest tenth. v in QIV, |v| = 29, = 80°
A) v = 28.6i + 5j
B) v = 28.6i - 5j
C) v = 5i + 28.6j
D) v = 5i - 28.6j
A) v = 28.6i + 5j
B) v = 28.6i - 5j
C) v = 5i + 28.6j
D) v = 5i - 28.6j

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
55
Use the following to answer questions :
u = -2i + j; v = 4i + 3j
Compute u - 5v.
A) -16i - 17j
B) -15i - 16j
C) -15i - 17j
D) -16i - 16j
u = -2i + j; v = 4i + 3j
Compute u - 5v.
A) -16i - 17j
B) -15i - 16j
C) -15i - 17j
D) -16i - 16j

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
56
Use the following to answer questions :
u = -2i + j; v = 4i + 3j
Compute u - v.
A) -8i + 4j
B) 8i - 4j
C) -10i + 2j
D) 0i + 8j
u = -2i + j; v = 4i + 3j
Compute u - v.
A) -8i + 4j
B) 8i - 4j
C) -10i + 2j
D) 0i + 8j

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
57
v = 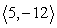 (a) Graph the vector.
(a) Graph the vector.
(b) Write the vector as a linear combination of i and j.
(c) Compute the magnitude of the vector.
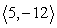 (a) Graph the vector.
(a) Graph the vector.(b) Write the vector as a linear combination of i and j.
(c) Compute the magnitude of the vector.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
58
The force vectors F1 = 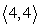 and F2 =
and F2 = 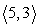 are acting on a common point P. Find an additional force vector so that equilibrium takes place.
are acting on a common point P. Find an additional force vector so that equilibrium takes place.
A)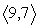
B)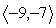
C)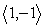
D)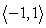
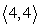 and F2 =
and F2 = 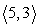 are acting on a common point P. Find an additional force vector so that equilibrium takes place.
are acting on a common point P. Find an additional force vector so that equilibrium takes place.A)
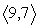
B)
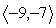
C)
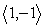
D)
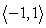

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
59
Use the following to answer questions :
u =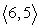 ; v =
; v = 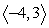
Compute u - 5v.
A)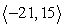
B)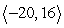
C)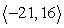
D)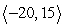
u =
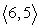 ; v =
; v = 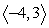
Compute u - 5v.
A)
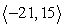
B)
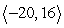
C)
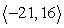
D)
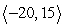

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
60
Use the following to answer questions :
u = -2i + j; v = 4i + 3j
Compute 2u + 5v.
A) -17i + 7j
B) -16i + 8j
C) -17i + 8j
D) -16i + 7j
u = -2i + j; v = 4i + 3j
Compute 2u + 5v.
A) -17i + 7j
B) -16i + 8j
C) -17i + 8j
D) -16i + 7j

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
61
Use the following to answer questions :
For a certain AC circuit, R = 35 , XL = 20 and XC = 8 , with I = 2 A.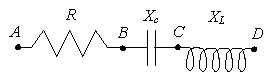
-Find the total voltage across the circuit.
A) 74V
B) 75V
C) 76V
D) 77V
For a certain AC circuit, R = 35 , XL = 20 and XC = 8 , with I = 2 A.

-Find the total voltage across the circuit.
A) 74V
B) 75V
C) 76V
D) 77V

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
62
Use the following to answer questions :
A projectile is launched from a catapult with initial velocity 350 feet/sec at an angle of 65°.
Find the position of the object after 4 seconds. Round to the nearest hundredth.
A) projectile is about 591.67 ft away and 1268.83 ft high.
B) projectile is about 591.67 ft away and 1012.83 ft high.
C) projectile is about 147.92 ft away and 1268.83 ft high.
D) projectile is about 147.92 ft away and 1012.83 ft high.
A projectile is launched from a catapult with initial velocity 350 feet/sec at an angle of 65°.
Find the position of the object after 4 seconds. Round to the nearest hundredth.
A) projectile is about 591.67 ft away and 1268.83 ft high.
B) projectile is about 591.67 ft away and 1012.83 ft high.
C) projectile is about 147.92 ft away and 1268.83 ft high.
D) projectile is about 147.92 ft away and 1012.83 ft high.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
63
Use the following to answer questions :
z1 = 3 - 4i
z2 = -1 - 3i
z3 = 4 - i
Express one complex number as the sum of the other two.
A) z1 = z2 + z3
B) z2 = z1 + z3
C) z3 = z1 + z2
D) not possible
z1 = 3 - 4i
z2 = -1 - 3i
z3 = 4 - i
Express one complex number as the sum of the other two.
A) z1 = z2 + z3
B) z2 = z1 + z3
C) z3 = z1 + z2
D) not possible

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
64
Use De Moivre's Theorem to compute 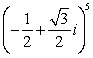 .
.
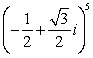 .
.
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
65
Use the following to answer questions : 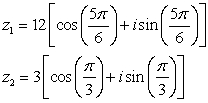
Compute the product z1z2 using the trigonometric form. Write your answer in exact rectangular form.
A)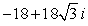
B)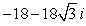
C)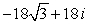
D)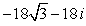
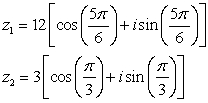
Compute the product z1z2 using the trigonometric form. Write your answer in exact rectangular form.
A)
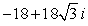
B)
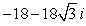
C)
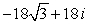
D)
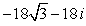

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
66
Use the following to answer questions :
z1 = 3 - 4i
z2 = -1 - 3i
z3 = 4 - i
Graph the complex numbers z1, z2, and z3 given.
A)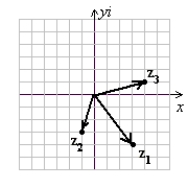
(Gridlines are spaced one unit apart.)
B)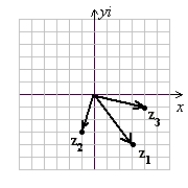
(Gridlines are spaced one unit apart.)
C)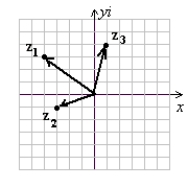
(Gridlines are spaced one unit apart.)
D)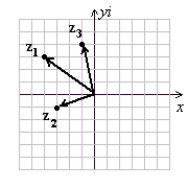
(Gridlines are spaced one unit apart.)
z1 = 3 - 4i
z2 = -1 - 3i
z3 = 4 - i
Graph the complex numbers z1, z2, and z3 given.
A)

(Gridlines are spaced one unit apart.)
B)

(Gridlines are spaced one unit apart.)
C)

(Gridlines are spaced one unit apart.)
D)

(Gridlines are spaced one unit apart.)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
67
For the complex numbers z1 = 1 - 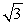 i and z2 = -5 + 0i
i and z2 = -5 + 0i
(a) Find the moduli r1 and r2 and the arguments 1 and 2.
(b) Compute the quotient in rectangular form.
(c) Find the modulus r and argument of the quotient.
(d) Verify that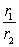 = r and 1 - 2 = .
= r and 1 - 2 = .
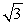 i and z2 = -5 + 0i
i and z2 = -5 + 0i(a) Find the moduli r1 and r2 and the arguments 1 and 2.
(b) Compute the quotient in rectangular form.
(c) Find the modulus r and argument of the quotient.
(d) Verify that
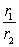 = r and 1 - 2 = .
= r and 1 - 2 = . 
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
68
Write the complex number in trigonometric form. Answer in radians using both an exact form and an approximate form, rounding to four decimal places.
-4 + 6i
-4 + 6i

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
69
Write the complex number in trigonometric form using degrees. -4 + 4i
A) 4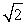 (cos 45° + i sin 45°)
(cos 45° + i sin 45°)
B) 32(cos 45° + i sin 45°)
C) 4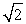 (cos 135° + i sin 135°)
(cos 135° + i sin 135°)
D) 32(cos 135° + i sin 135°)
A) 4
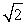 (cos 45° + i sin 45°)
(cos 45° + i sin 45°)B) 32(cos 45° + i sin 45°)
C) 4
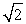 (cos 135° + i sin 135°)
(cos 135° + i sin 135°)D) 32(cos 135° + i sin 135°)

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
70
Use the following to answer questions : 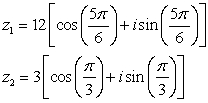
Compute the quotient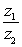 using the trigonometric form. Write your answer in exact rectangular form.
using the trigonometric form. Write your answer in exact rectangular form.
A) 4
B) -4
C) 4i
D) -4i
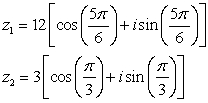
Compute the quotient
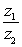 using the trigonometric form. Write your answer in exact rectangular form.
using the trigonometric form. Write your answer in exact rectangular form.A) 4
B) -4
C) 4i
D) -4i

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
71
Use the following to answer questions :
For a certain AC circuit, R = 35 , XL = 20 and XC = 8 , with I = 2 A.
-Find the magnitude of Z, the phase angle between current and voltage, and write the result in trigonometric form.
A) 37 cis 68.2°
B) 37 cis 18.9°
C) 38 cis 68.2°
D) 38 cis 18.9°
For a certain AC circuit, R = 35 , XL = 20 and XC = 8 , with I = 2 A.

-Find the magnitude of Z, the phase angle between current and voltage, and write the result in trigonometric form.
A) 37 cis 68.2°
B) 37 cis 18.9°
C) 38 cis 68.2°
D) 38 cis 18.9°

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
72
Graph the complex number using its trigonometric form, then convert it to rectangular form. 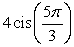
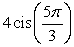

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
73
Use the following to answer questions :
A projectile is launched from a catapult with initial velocity 350 feet/sec at an angle of 65°.
Find the time(s) required to reach a height of 200 feet? Round to the nearest hundredth.
A) approximately 0.65 sec.
B) approximately 20.30 sec.
C) approximately 0.65 sec. and 19.17 sec.
D) approximately 0.65 sec. and 20.30 sec.
A projectile is launched from a catapult with initial velocity 350 feet/sec at an angle of 65°.
Find the time(s) required to reach a height of 200 feet? Round to the nearest hundredth.
A) approximately 0.65 sec.
B) approximately 20.30 sec.
C) approximately 0.65 sec. and 19.17 sec.
D) approximately 0.65 sec. and 20.30 sec.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
74
Use the following to answer questions :
u =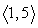 ; v =
; v = 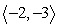
Find the projection of u along v (compute projvu). Round to the nearest hundredth as necessary.
A)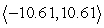
B)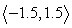
C)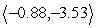
D)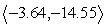
u =
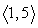 ; v =
; v = 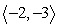
Find the projection of u along v (compute projvu). Round to the nearest hundredth as necessary.
A)
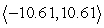
B)
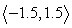
C)
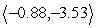
D)
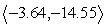

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
75
Use De Moivre's Theorem to compute (4 + 4i)4.
A) 1024
B) -1024
C) 1024i
D) -1024i
A) 1024
B) -1024
C) 1024i
D) -1024i

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
76
Use De Moivre's Theorem to verify z = -1 + i is a solution to z4 - 2z3 - z2 + 2z + 10 = 0.

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
77
Convert the complex number to rectangular form. 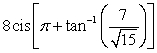
A)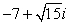
B)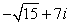
C)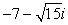
D)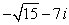
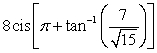
A)
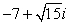
B)
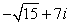
C)
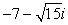
D)
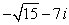

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
78
For the complex numbers z1 = 3 + 3i and z2 = -2 - 2i
(a) Find the moduli r1 and r2 and the arguments 1 and 2.
(b) Compute their product in rectangular form.
(c) Find the modulus r and argument of the product.
(d) Verify that r1r2 = r and 1 + 2 = .
(a) Find the moduli r1 and r2 and the arguments 1 and 2.
(b) Compute their product in rectangular form.
(c) Find the modulus r and argument of the product.
(d) Verify that r1r2 = r and 1 + 2 = .

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
79
Use the following to answer questions : 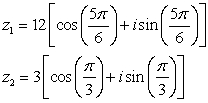
Compute the product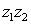 and the quotient
and the quotient 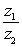 using the trigonometric form. Write your answer in rectangular form. Round to two decimal places as necessary.
using the trigonometric form. Write your answer in rectangular form. Round to two decimal places as necessary. 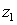 = 15(cos 72° + i sin 72°),
= 15(cos 72° + i sin 72°), 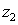 = 2.5(cos 36° + i sin 36°)
= 2.5(cos 36° + i sin 36°)
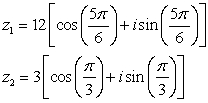
Compute the product
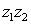 and the quotient
and the quotient 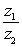 using the trigonometric form. Write your answer in rectangular form. Round to two decimal places as necessary.
using the trigonometric form. Write your answer in rectangular form. Round to two decimal places as necessary. 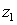 = 15(cos 72° + i sin 72°),
= 15(cos 72° + i sin 72°), 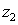 = 2.5(cos 36° + i sin 36°)
= 2.5(cos 36° + i sin 36°)
Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck
80
Use the following to answer questions :
u =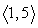 ; v =
; v = 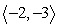
-Resolve u into vectors u1 and u2 where u1 || v and u2 v. Round to the nearest hundredth as necessary.
A) u1 =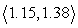 , u2 =
, u2 =
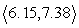
B) u1 =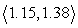 , u2 =
, u2 =
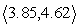
C) u1 =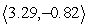 , u2 =
, u2 =
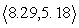
D) u1 =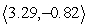 , u2 =
, u2 =
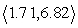
u =
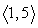 ; v =
; v = 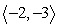
-Resolve u into vectors u1 and u2 where u1 || v and u2 v. Round to the nearest hundredth as necessary.
A) u1 =
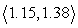 , u2 =
, u2 =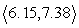
B) u1 =
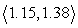 , u2 =
, u2 =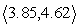
C) u1 =
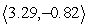 , u2 =
, u2 =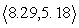
D) u1 =
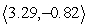 , u2 =
, u2 =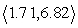

Unlock Deck
Unlock for access to all 86 flashcards in this deck.
Unlock Deck
k this deck


