Deck 6: Trigonometric Identities, Inverses, and Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/97
Play
Full screen (f)
Deck 6: Trigonometric Identities, Inverses, and Equations
1
Starting with the ratio identity given, use substitution and fundamental identities to write a new identity belonging to the ratio family. 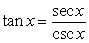
A)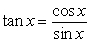
B)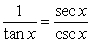
C)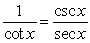
D)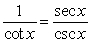
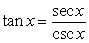
A)
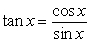
B)
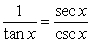
C)
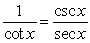
D)
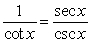
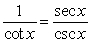
2
Write csc x entirely in terms of tan x.
A)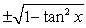
B)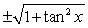
C)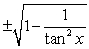
D)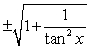
A)
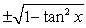
B)
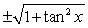
C)
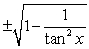
D)
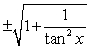
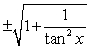
3
Use algebra and fundamental identities to rewrite the given expression to create a new identity relationship.
8 sec x tan x
8 sec x tan x
8 sec x tan x = 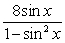 (Answers may vary.)
(Answers may vary.)
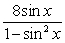 (Answers may vary.)
(Answers may vary.) 4
Verify that the equation is an identity. 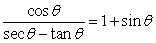
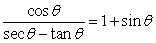

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
5
Verify that the equation is an identity. 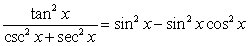
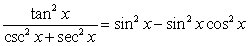

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
6
Find the exact value of the expression using a sum or difference identity. Some simplifications may involve using symmetry and the formula for negatives. cos 165°
A)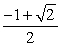
B)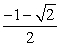
C)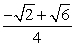
D)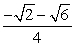
A)
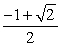
B)
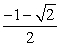
C)
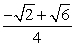
D)
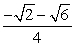

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
7
Write cot x entirely in terms of cos x.

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
8
Verify the equation is an identity using multiplication and fundamental identities.
cos x (sec x - cos x) =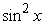
cos x (sec x - cos x) =
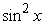

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
9
Show that the equation is not an identity. 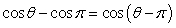
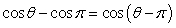

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
10
For the function f( ) and the quadrant in which terminates, state the value of the other five trig functions. 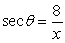 with in QIV.
with in QIV.
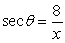 with in QIV.
with in QIV. 
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
11
Verify the equation is an identity using special products and fundamental identities.
(1 + cos x)[1 - cos(-x)] = sin2 x
(1 + cos x)[1 - cos(-x)] = sin2 x

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
12
For the function 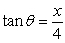 and the quadrant QI in which terminates, state the value of sin .
and the quadrant QI in which terminates, state the value of sin .
A)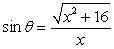
B)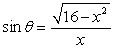
C)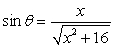
D)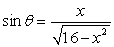
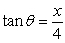 and the quadrant QI in which terminates, state the value of sin .
and the quadrant QI in which terminates, state the value of sin .A)
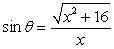
B)
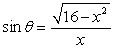
C)
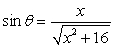
D)
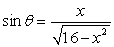

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
13
Verify that the equation is an identity. 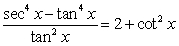
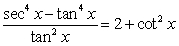

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
14
Use algebra and fundamental identities to rewrite the given expression to create a new identity relationship. csc x + cot x
A) csc x + cot x =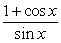
B) csc x + cot x =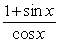
C) csc x + cot x = tan x
D) csc x + cot x = 1 + sin2 x
A) csc x + cot x =
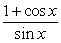
B) csc x + cot x =
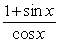
C) csc x + cot x = tan x
D) csc x + cot x = 1 + sin2 x

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
15
Rewrite as a single expression. cos(6 )cos(2 ) + sin(6 )sin(2 )
A) cos(8 )
B) cos(4 )
C) sin(8 )
D) sin(4 )
A) cos(8 )
B) cos(4 )
C) sin(8 )
D) sin(4 )

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
16
Show that the equation is not an identity. 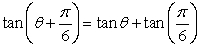
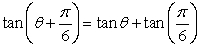

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
17
Verify the equation is an identity using factoring and fundamental identities. 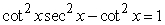
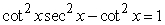

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
18
Verify the equation is an identity by using fundamental identities and 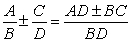 to combine terms.
to combine terms. 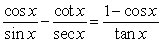
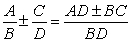 to combine terms.
to combine terms. 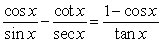

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
19
Verify that the equation is an identity. 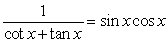
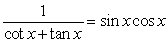

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
20
Verify the equation is an identity using special products and fundamental identities. 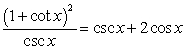
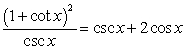

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
21
Find the exact value. 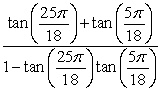
A)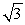
B)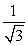
C)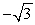
D)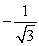
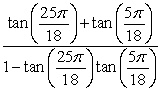
A)
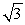
B)
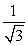
C)
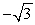
D)
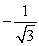

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
22
Rewrite as a single expression. 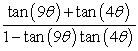
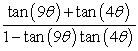

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
23
Use the following to answer questions :
and are acute angles with tan( ) =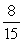 and sec( ) =
and sec( ) = 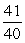 .
.
-Find cos( - ).
A)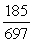
B)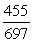
C)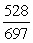
D)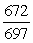
and are acute angles with tan( ) =
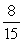 and sec( ) =
and sec( ) = 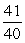 .
.-Find cos( - ).
A)
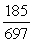
B)
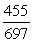
C)
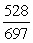
D)
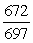

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
24
Use the following to answer questions :
and are acute angles with tan( ) =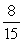 and sec( ) =
and sec( ) = 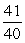 .
.
-Find tan( - ).
A)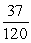
B)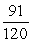
C)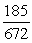
D)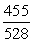
and are acute angles with tan( ) =
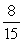 and sec( ) =
and sec( ) = 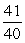 .
.-Find tan( - ).
A)
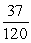
B)
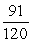
C)
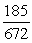
D)
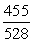

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
25
Use a cofunction identity to write an equivalent expression.
cos 13°
cos 13°

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
26
Verify the identity. 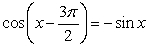
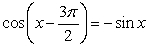

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
27
Use an angle reduction formula to find the exact value. sin 2940°
A)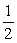
B)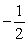
C)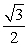
D)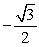
A)
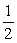
B)
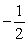
C)
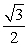
D)
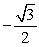

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
28
Rewrite as a single expression. sin(7 )cos(3 ) + cos(7 )sin(3 )
A) cos(10 )
B) cos(4 )
C) sin(10 )
D) sin(4 )
A) cos(10 )
B) cos(4 )
C) sin(10 )
D) sin(4 )

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
29
Use the following to answer questions :
and are acute angles with tan( ) =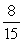 and sec( ) =
and sec( ) = 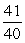 .
.
-Find sin( - ).
A)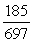
B)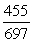
C)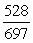
D)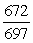
and are acute angles with tan( ) =
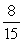 and sec( ) =
and sec( ) = 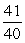 .
.-Find sin( - ).
A)
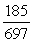
B)
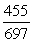
C)
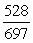
D)
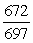

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
30
Find the exact value. sin 190° cos 55° - cos 190° sin 55°
A)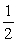
B)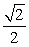
C)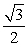
D)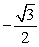
A)
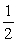
B)
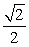
C)
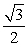
D)
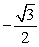

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
31
Rewrite as a single expression. 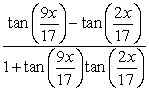
A)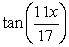
B)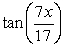
C)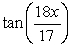
D)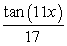
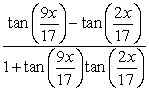
A)
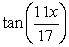
B)
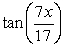
C)
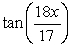
D)
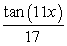

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
32
Use the following to answer questions :
and are acute angles with tan( ) =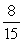 and sec( ) =
and sec( ) = 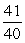 .
.
-Find tan( + ).
A)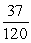
B)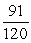
C)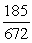
D)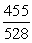
and are acute angles with tan( ) =
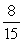 and sec( ) =
and sec( ) = 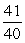 .
.-Find tan( + ).
A)
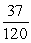
B)
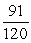
C)
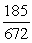
D)
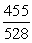

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
33
Use the following to answer questions :
and are acute angles with tan( ) =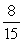 and sec( ) =
and sec( ) = 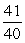 .
.
-Find cos( + ).
A)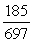
B)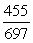
C)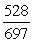
D)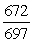
and are acute angles with tan( ) =
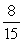 and sec( ) =
and sec( ) = 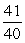 .
.-Find cos( + ).
A)
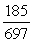
B)
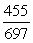
C)
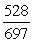
D)
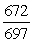

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
34
Use a cofunction identity to write an equivalent expression. 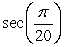
A)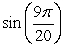
B)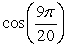
C)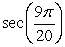
D)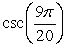
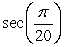
A)
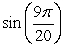
B)
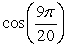
C)
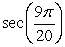
D)
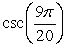

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
35
Find the exact value using a sum or difference identity. Some simplifications may involve using symmetry and the formulas for negatives.
sin(-15°)
sin(-15°)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
36
Find the exact value using a sum or difference identity. Some simplifications may involve using symmetry and the formulas for negatives. 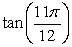
A)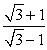
B)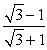
C)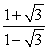
D)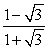
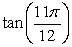
A)
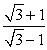
B)
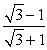
C)
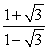
D)
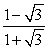

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
37
Rewrite as a single expression. cos(10 )cos(6 ) - sin(10 )sin(6 )
A) cos(16 )
B) cos(4 )
C) sin(16 )
D) sin(4 )
A) cos(16 )
B) cos(4 )
C) sin(16 )
D) sin(4 )

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
38
Find the exact value. 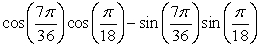
A)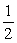
B)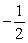
C)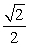
D)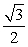
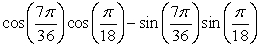
A)
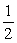
B)
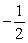
C)
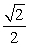
D)
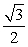

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
39
Use the following to answer questions :
and are acute angles with tan( ) =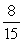 and sec( ) =
and sec( ) = 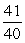 .
.
-Find sin( + ).
A)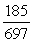
B)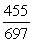
C)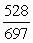
D)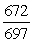
and are acute angles with tan( ) =
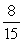 and sec( ) =
and sec( ) = 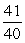 .
.-Find sin( + ).
A)
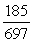
B)
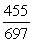
C)
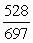
D)
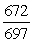

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
40
Rewrite as a single expression. sin(6 )cos(3 ) - cos(6 )sin(3 )
A) cos(9 )
B) cos(3 )
C) sin(9 )
D) sin(3 )
A) cos(9 )
B) cos(3 )
C) sin(9 )
D) sin(3 )

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
41
Find exact values for 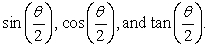
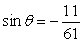 ;
; 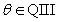
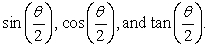
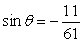 ;
; 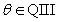

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
42
Use a half-angle identity to rewrite the expression as a single, non-radical function. 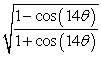
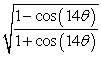

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
43
Find the exact value using a product-to-sum identity. 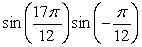
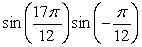

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
44
Use the following to answer questions :
tan =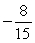 ; in QII.
; in QII.
-Find the exact value of sin(2 ).
A)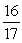
B)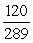
C)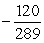
D)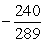
tan =
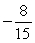 ; in QII.
; in QII.-Find the exact value of sin(2 ).
A)
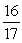
B)
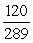
C)
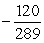
D)
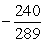

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
45
Use a double-angle identity to find the exact value. cos 105° sin 105°
A)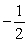
B)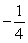
C)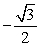
D)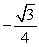
A)
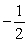
B)
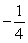
C)
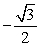
D)
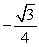

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
46
Find the exact values for sin , cos , and tan . 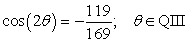
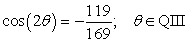

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
47
Rewrite in terms of an expression containing only cosines to the power 1.
sin2 x cos4 x
sin2 x cos4 x

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
48
Rewrite the product as a sum using a product-to-sum identity. sin(-10 )sin(4 )
A)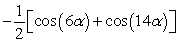
B)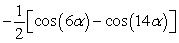
C)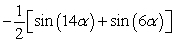
D)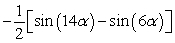
A)
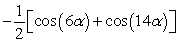
B)
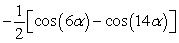
C)
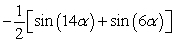
D)
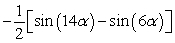

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
49
Rewrite the sum as a product using a sum-to-product identity. 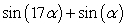
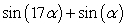

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
50
Find the exact value using a sum-to-product identity. 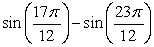
A)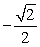
B) -1
C)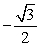
D)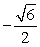
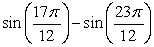
A)
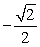
B) -1
C)
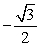
D)
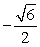

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
51
Use a double-angle identity to find the exact value. 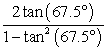
A) 0
B) 1
C) -1
D)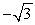
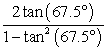
A) 0
B) 1
C) -1
D)
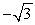

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
52
Rewrite the product as a sum using a product-to-sum identity. cos(10 )sin(-7 )
A)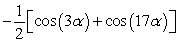
B)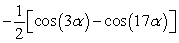
C)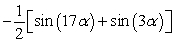
D)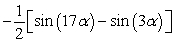
A)
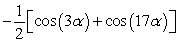
B)
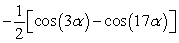
C)
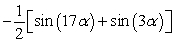
D)
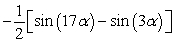

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
53
Use the following to answer questions :
tan =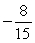 ; in QII.
; in QII.
-Find the exact value of tan(2 ).
A)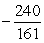
B)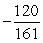
C)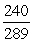
D)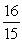
tan =
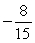 ; in QII.
; in QII.-Find the exact value of tan(2 ).
A)
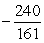
B)
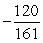
C)
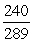
D)
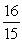

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
54
Rewrite the sum as a product using a sum-to-product identity. 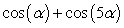
A) 2cos(3 )sin(2 )
B) 2sin(3 )cos(2 )
C) 2cos(3 )cos(2 )
D) 2sin(3 )sin(2 )
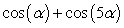
A) 2cos(3 )sin(2 )
B) 2sin(3 )cos(2 )
C) 2cos(3 )cos(2 )
D) 2sin(3 )sin(2 )

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
55
Use the following to answer questions : 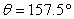
-Use a half-angle identity to find the exact value of cos .
A)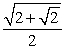
B)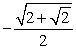
C)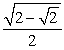
D)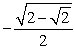
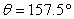
-Use a half-angle identity to find the exact value of cos .
A)
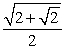
B)
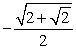
C)
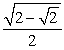
D)
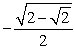

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
56
Rewrite the product as a sum using a product-to-sum identity.
2sin(2073\9\pi\)t)cos(813 t)
2sin(2073\9\pi\)t)cos(813 t)

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
57
Use the following to answer questions :
tan =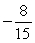 ; in QII.
; in QII.
-Find the exact value of cos(2 ).
A)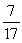
B)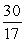
C)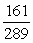
D)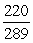
tan =
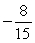 ; in QII.
; in QII.-Find the exact value of cos(2 ).
A)
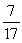
B)
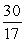
C)
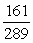
D)
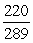

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
58
Use the following to answer questions : 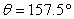
-Use a half-angle identity to find the exact value of tan .
A)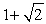
B)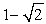
C)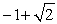
D)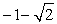
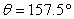
-Use a half-angle identity to find the exact value of tan .
A)
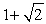
B)
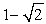
C)
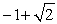
D)
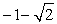

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
59
Use a double-angle identity to find the exact value. 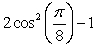
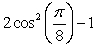

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
60
Use the following to answer questions : 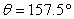
-Use a half-angle identity to find the exact value of sin .
A)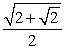
B)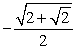
C)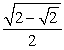
D)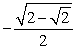
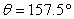
-Use a half-angle identity to find the exact value of sin .
A)
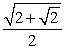
B)
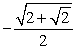
C)
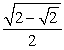
D)
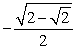

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
61
Evaluate without the aid of calculators or tables. Answer in radians.
cos-1 1
cos-1 1

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
62
Simplify without using a calculator. 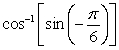
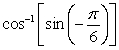

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
63
Evaluate without using a calculator. Answer in radians. 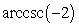
A)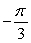
B)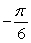
C)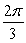
D)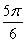
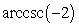
A)
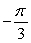
B)
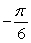
C)
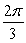
D)
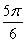

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
64
Verify the identity. 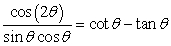
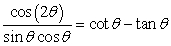

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
65
Evaluate without the aid of calculators or tables, keeping the domain and range of the function in mind. Answer in radians. 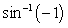
A) 0
B)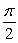
C)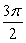
D)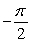
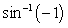
A) 0
B)
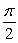
C)
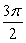
D)
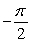

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
66
Use the following to answer questions :
The graph of y = csc(x) is shown below. Draw the horizontal line y = -1.5.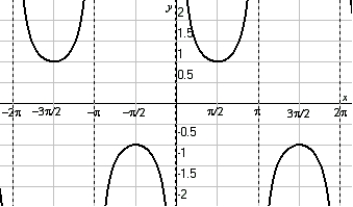
State the quadrant of the principal root.
A) QI
B) QII
C) QIII
D) QIV
The graph of y = csc(x) is shown below. Draw the horizontal line y = -1.5.

State the quadrant of the principal root.
A) QI
B) QII
C) QIII
D) QIV

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
67
Evaluate. Answer in exact form. 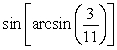
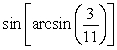

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
68
Evaluate without using a calculator. Answer in radians. 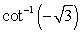
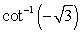

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
69
Evaluate. Answer in exact form. 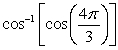
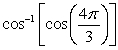

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
70
Evaluate without the aid of calculators or tables. Answer in radians. 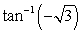
A)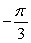
B)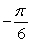
C)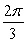
D)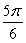
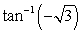
A)
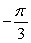
B)
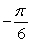
C)
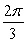
D)
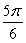

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
71
Evaluate using a calculator. Answer to the nearest tenth of a degree.
sec-1 5.593
sec-1 5.593

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
72
Evaluate using a calculator. Answer in radians to the nearest ten-thousandth, in degrees to the nearest tenth. 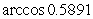
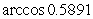

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
73
Evaluate using a calculator, keeping the domain and range of the function in mind. Answer in radians to the nearest ten-thousandth and in degrees to the nearest tenth. 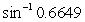
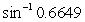

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
74
Evaluate without the aid of calculators or tables. Answer in radians. 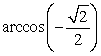
A)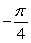
B)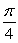
C)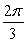
D)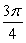
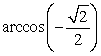
A)
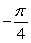
B)
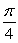
C)
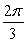
D)
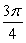

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
75
The range of a projectile is modeled by the function 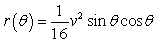 , where v is the initial velocity and is the angle at which the object is initially propelled. The maximum range is achieved when = 45°. Use exact values to compute how many feet short of maximum the projectile falls if = 67.5° and v = 104 ft/sec.
, where v is the initial velocity and is the angle at which the object is initially propelled. The maximum range is achieved when = 45°. Use exact values to compute how many feet short of maximum the projectile falls if = 67.5° and v = 104 ft/sec.
A)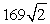 feet
feet
B)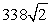 feet
feet
C)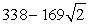 feet
feet
D)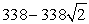 feet
feet
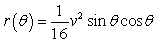 , where v is the initial velocity and is the angle at which the object is initially propelled. The maximum range is achieved when = 45°. Use exact values to compute how many feet short of maximum the projectile falls if = 67.5° and v = 104 ft/sec.
, where v is the initial velocity and is the angle at which the object is initially propelled. The maximum range is achieved when = 45°. Use exact values to compute how many feet short of maximum the projectile falls if = 67.5° and v = 104 ft/sec.A)
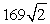 feet
feetB)
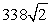 feet
feetC)
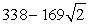 feet
feetD)
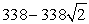 feet
feet
Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
76
Use the following to answer questions :
The graph of y = csc(x) is shown below. Draw the horizontal line y = -1.5.![<strong>Use the following to answer questions : The graph of y = csc(x) is shown below. Draw the horizontal line y = -1.5. -State the number of roots in [0, 2 \pi ].</strong> A) 4 B) 3 C) 2 D) 1](https://storage.examlex.com/TB3307/11ea7f29_4fff_2857_9ecd_413ead042859_TB3307_00_TB3307_00_TB3307_00.jpg)
-State the number of roots in [0, 2 ].
A) 4
B) 3
C) 2
D) 1
The graph of y = csc(x) is shown below. Draw the horizontal line y = -1.5.
![<strong>Use the following to answer questions : The graph of y = csc(x) is shown below. Draw the horizontal line y = -1.5. -State the number of roots in [0, 2 \pi ].</strong> A) 4 B) 3 C) 2 D) 1](https://storage.examlex.com/TB3307/11ea7f29_4fff_2857_9ecd_413ead042859_TB3307_00_TB3307_00_TB3307_00.jpg)
-State the number of roots in [0, 2 ].
A) 4
B) 3
C) 2
D) 1

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
77
Evaluate using a calculator, keeping in mind the domain and range of the function. Answer in radians to the nearest ten-thousandth and in degrees to the nearest tenth. 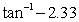
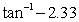

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
78
Evaluate without the aid of calculators or tables, keeping the domain and range of the function in mind. Answer in radians. 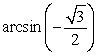
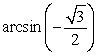

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
79
Evaluate. Answer in exact form. 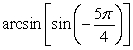
A)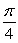
B)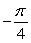
C)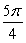
D)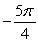
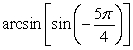
A)
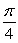
B)
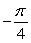
C)
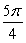
D)
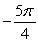

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck
80
Evaluate. Answer in exact form. 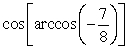
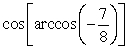

Unlock Deck
Unlock for access to all 97 flashcards in this deck.
Unlock Deck
k this deck


