Deck 9: Analytical Geometry
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/122
Play
Full screen (f)
Deck 9: Analytical Geometry
1
Three non-colinear points are given and can be connected with line segments to form a triangle. Find the perimeter of the triangle (rounded to the nearest tenth as needed) and determine if the triangle is a right triangle.
P1 = (3, 6)
P2 = (0, 6)
P3 = (7, -3)
P1 = (3, 6)
P2 = (0, 6)
P3 = (7, -3)
perimeter: 24.3; not a right triangle
2
Line segments ( 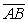 ) and (
) and ( 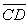 ) have the endpoints indicated. Use the slope formula to determine if the segments are parallel, perpendicular or simply intersect. A(-3, 4) B(5, -2)
) have the endpoints indicated. Use the slope formula to determine if the segments are parallel, perpendicular or simply intersect. A(-3, 4) B(5, -2)
C(-4, 3) D(3, 5)
A) parallel
B) perpendicular
C) intersect
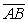 ) and (
) and ( 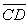 ) have the endpoints indicated. Use the slope formula to determine if the segments are parallel, perpendicular or simply intersect. A(-3, 4) B(5, -2)
) have the endpoints indicated. Use the slope formula to determine if the segments are parallel, perpendicular or simply intersect. A(-3, 4) B(5, -2)C(-4, 3) D(3, 5)
A) parallel
B) perpendicular
C) intersect
intersect
3
A theorem from elementary geometry states: If P1 and P2 are on opposite sides of a line segment and an equal distance from the endpoints, then the line through P1 and P2 is a perpendicular bisector of the segment. Verify this is true for the segment and points shown. 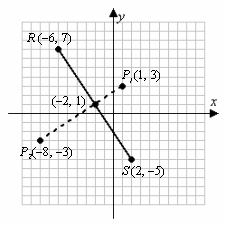

First show that the conditions of the statement are met.
Although it is evident from the graph that P1 and P2 are on opposite sides of the line segment , it can be proven using the equation of the line
, it can be proven using the equation of the line  .
.
Find the slope of this line using the endpoints of , R (-6, 7) and S (2, -5) and the slope formula:
, R (-6, 7) and S (2, -5) and the slope formula: 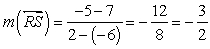 and use the slope-point to find the equation of the line:
and use the slope-point to find the equation of the line: 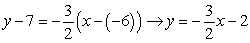 It can then be shown that P1(1, 3) is in the half-plane
It can then be shown that P1(1, 3) is in the half-plane 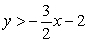 :
: 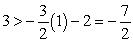 and P2(-8, -3) is in the half-plane
and P2(-8, -3) is in the half-plane 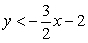 :
: 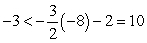 and they are therefore on opposite sides of the line segment
and they are therefore on opposite sides of the line segment 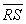 .
.
Next, use the distance formula to show that P1(1, 3) is an equal distance from the endpoints R (-6, 7) and S (2, -5):
d(P1R)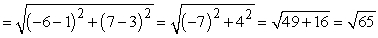 d(P1S)
d(P1S) 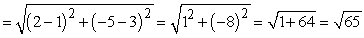 and that P2(-8, -3) is an equal distance from the endpoints R (-6, 7) and S (2, -5):
and that P2(-8, -3) is an equal distance from the endpoints R (-6, 7) and S (2, -5):
d(P2R)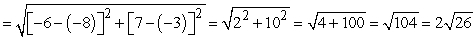 d(P2S)
d(P2S) 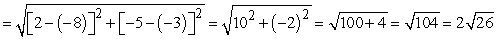 Now show that the line
Now show that the line 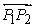 is a perpendicular bisector of
is a perpendicular bisector of 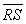 .
.
Use the slope formula to find the slope of the line through P1(1, 3) and P2(-8, -3):
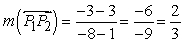 Since
Since 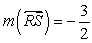 from first step,
from first step, 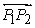 and
and 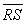 are perpendicular.
are perpendicular.
Use the point-slope formula to find the equation of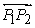 :
: 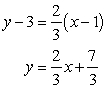 Find the midpoint of
Find the midpoint of 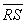 :
: 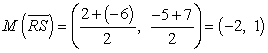 Show
Show 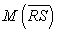 is on
is on 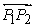 :
: 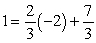 Therefore
Therefore 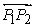 is a perpendicular bisector of
is a perpendicular bisector of 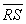 .
.
Although it is evident from the graph that P1 and P2 are on opposite sides of the line segment
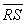 , it can be proven using the equation of the line
, it can be proven using the equation of the line 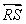 .
.Find the slope of this line using the endpoints of
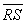 , R (-6, 7) and S (2, -5) and the slope formula:
, R (-6, 7) and S (2, -5) and the slope formula: 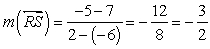 and use the slope-point to find the equation of the line:
and use the slope-point to find the equation of the line: 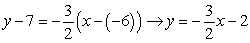 It can then be shown that P1(1, 3) is in the half-plane
It can then be shown that P1(1, 3) is in the half-plane 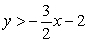 :
: 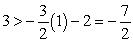 and P2(-8, -3) is in the half-plane
and P2(-8, -3) is in the half-plane 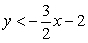 :
: 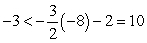 and they are therefore on opposite sides of the line segment
and they are therefore on opposite sides of the line segment  .
.Next, use the distance formula to show that P1(1, 3) is an equal distance from the endpoints R (-6, 7) and S (2, -5):
d(P1R)
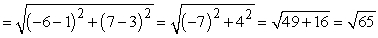 d(P1S)
d(P1S) 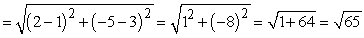 and that P2(-8, -3) is an equal distance from the endpoints R (-6, 7) and S (2, -5):
and that P2(-8, -3) is an equal distance from the endpoints R (-6, 7) and S (2, -5):d(P2R)
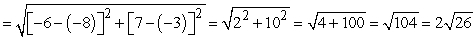 d(P2S)
d(P2S) 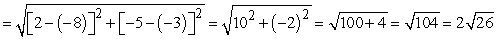 Now show that the line
Now show that the line 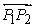 is a perpendicular bisector of
is a perpendicular bisector of 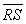 .
.Use the slope formula to find the slope of the line through P1(1, 3) and P2(-8, -3):
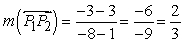 Since
Since 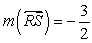 from first step,
from first step, 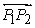 and
and 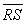 are perpendicular.
are perpendicular.Use the point-slope formula to find the equation of
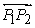 :
: 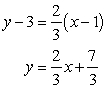 Find the midpoint of
Find the midpoint of 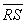 :
: 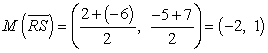 Show
Show 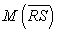 is on
is on  :
: 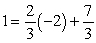 Therefore
Therefore 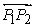 is a perpendicular bisector of
is a perpendicular bisector of 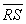 .
. 4
A theorem from elementary geometry states: If the diagonals of a quadrilateral have equal length and bisect each other, then the quadrilateral is a rectangle. Verify the points A(-1, 4), B(5, 1), C(3, -3), and D(-3, 0) are the vertices of a rectangle.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
5
Line segments ( 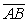 ) and (
) and ( 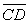 ) have the endpoints indicated. Use the slope formula to determine if the segments are parallel, perpendicular or simply intersect. A(-1, 4) B(1, -6)
) have the endpoints indicated. Use the slope formula to determine if the segments are parallel, perpendicular or simply intersect. A(-1, 4) B(1, -6)
C(-5, 0) D(5, 2)
A) parallel
B) perpendicular
C) intersect
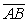 ) and (
) and ( 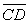 ) have the endpoints indicated. Use the slope formula to determine if the segments are parallel, perpendicular or simply intersect. A(-1, 4) B(1, -6)
) have the endpoints indicated. Use the slope formula to determine if the segments are parallel, perpendicular or simply intersect. A(-1, 4) B(1, -6)C(-5, 0) D(5, 2)
A) parallel
B) perpendicular
C) intersect

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
6
Complete the square in both x and y to write the equation in standard form. 4x2 + 16y2 + 16x - 64y + 16 = 0
A)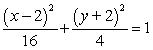
B)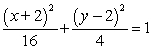
C)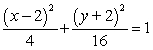
D)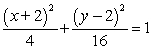
A)
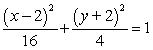
B)
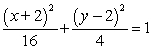
C)
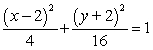
D)
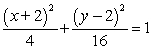

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
7
Write the equation in standard form and identify the center and the values of a and b.
x2 + 9y2 = 36
x2 + 9y2 = 36

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
8
Identify the equation as that of an ellipse or a circle. 5(x - 5)2 + 5(y + 7)2 = 80.
A) ellipse
B) circle
A) ellipse
B) circle

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
9
Write the equation in standard form and sketch the graph.
x2 + 9y2 = 36
x2 + 9y2 = 36

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
10
Graph the hyperbola. Label the vertices. 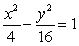
A)
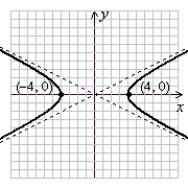
(Gridlines are spaced one unit apart.)
B)
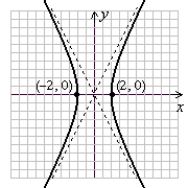
(Gridlines are spaced one unit apart.)
C)
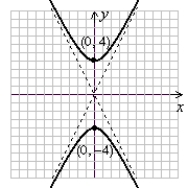
(Gridlines are spaced one unit apart.)
D)
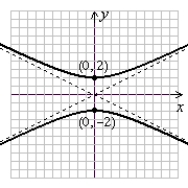
(Gridlines are spaced one unit apart.)
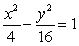
A)

(Gridlines are spaced one unit apart.)
B)

(Gridlines are spaced one unit apart.)
C)

(Gridlines are spaced one unit apart.)
D)

(Gridlines are spaced one unit apart.)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
11
Complete the square in both x and y to write the equation in standard form. Then draw a complete graph of the relation and identify all important features.
9x2 + 4y2 - 18x + 16y - 11 = 0
9x2 + 4y2 - 18x + 16y - 11 = 0

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
12
Show the figure drawn by connecting points A(-3, 1), B(4, -5), C(5, -1), and D(-2, 5) is a parallelogram (opposite sides parallel and equal in length).

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
13
Of the following four points, three are an equal distance from the point P(3, 4) and one is not. Identify which three.
Q(6, 8) R(-1, 1) S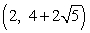
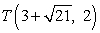
A) Q, R, S
B) Q, R, T
C) Q, S, T
D) R, S, T
Q(6, 8) R(-1, 1) S
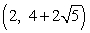
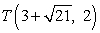
A) Q, R, S
B) Q, R, T
C) Q, S, T
D) R, S, T

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
14
Find two additional points that are the same (non-vertical, non-horizontal) distance from the point P(-5, 2) as S 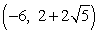 .
.
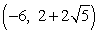 .
.
Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
15
Sketch the graph of the ellipse. 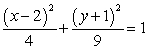
A)
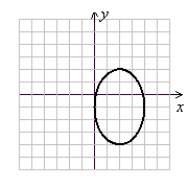
(Gridlines are spaced one unit apart.)
B)
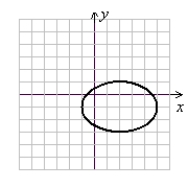
(Gridlines are spaced one unit apart.)
C)
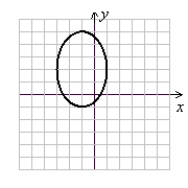
(Gridlines are spaced one unit apart.)
D)
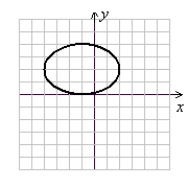
(Gridlines are spaced one unit apart.)
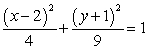
A)

(Gridlines are spaced one unit apart.)
B)

(Gridlines are spaced one unit apart.)
C)

(Gridlines are spaced one unit apart.)
D)

(Gridlines are spaced one unit apart.)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
16
Identify the equation as that of an ellipse or a circle. 9(x - 7)2 + 4(y + 6)2 = 36.
A) ellipse
B) circle
A) ellipse
B) circle

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
17
Line segments ( 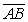 ) and (
) and (  ) have the endpoints indicated. Use the slope formula to determine if the segments are parallel, perpendicular or simply intersect. A(-4, 2) B(3, -4)
) have the endpoints indicated. Use the slope formula to determine if the segments are parallel, perpendicular or simply intersect. A(-4, 2) B(3, -4)
C(-2, 5) D(5, -1)
A) parallel
B) perpendicular
C) intersect
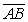 ) and (
) and (  ) have the endpoints indicated. Use the slope formula to determine if the segments are parallel, perpendicular or simply intersect. A(-4, 2) B(3, -4)
) have the endpoints indicated. Use the slope formula to determine if the segments are parallel, perpendicular or simply intersect. A(-4, 2) B(3, -4)C(-2, 5) D(5, -1)
A) parallel
B) perpendicular
C) intersect

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
18
Sketch the graph of the ellipse. 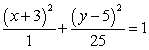
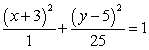

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
19
Three non-colinear points are given and can be connected with line segments to form a triangle. Find the perimeter of the triangle (rounded to the nearest tenth as needed) and determine if the triangle is a right triangle. P1 = (-8, 2)
P2 = (-8, -6)
P3 = (7, 2)
A) perimeter: 33.0; right triangle
B) perimeter: 40.0; not a right triangle
C) perimeter: 40.0; right triangle
D) perimeter: 33.0; not a right triangle
P2 = (-8, -6)
P3 = (7, 2)
A) perimeter: 33.0; right triangle
B) perimeter: 40.0; not a right triangle
C) perimeter: 40.0; right triangle
D) perimeter: 33.0; not a right triangle

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
20
Graph the hyperbola. Label the vertices. 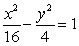
A)
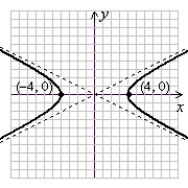
(Gridlines are spaced one unit apart.)
B)
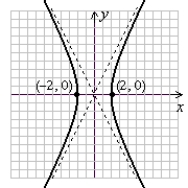
(Gridlines are spaced one unit apart.)
C)
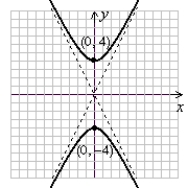
(Gridlines are spaced one unit apart.)
D)
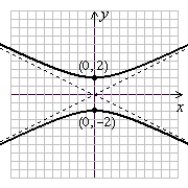
(Gridlines are spaced one unit apart.)
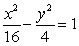
A)

(Gridlines are spaced one unit apart.)
B)

(Gridlines are spaced one unit apart.)
C)

(Gridlines are spaced one unit apart.)
D)

(Gridlines are spaced one unit apart.)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
21
Use the following to answer questions :
y = 2x2 - x - 3
Find the x- and y-intercepts (if they exist).
A) x-intercepts: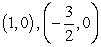 ; y-intercept: (0, 3)
; y-intercept: (0, 3)
B) x-intercepts: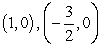 ; y-intercept: (0, -3)
; y-intercept: (0, -3)
C) x-intercepts: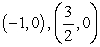 ; y-intercept: (0, -3)
; y-intercept: (0, -3)
D) x-intercepts: none; y-intercept: (0, -3)
y = 2x2 - x - 3
Find the x- and y-intercepts (if they exist).
A) x-intercepts:
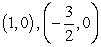 ; y-intercept: (0, 3)
; y-intercept: (0, 3)B) x-intercepts:
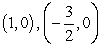 ; y-intercept: (0, -3)
; y-intercept: (0, -3)C) x-intercepts:
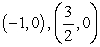 ; y-intercept: (0, -3)
; y-intercept: (0, -3)D) x-intercepts: none; y-intercept: (0, -3)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
22
Classify the equation as that of a circle, ellipse, hyperbola, or none of the above. 4x2 + 9y2 - 40x - 18y = -73
A) Circle
B) Ellipse
C) Hyperbola
D) None of these
A) Circle
B) Ellipse
C) Hyperbola
D) None of these

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
23
Sketch a complete graph of the equation, including asymptotes. Be sure to identify the center and vertices. 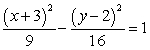
A)
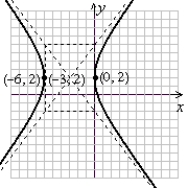
B)
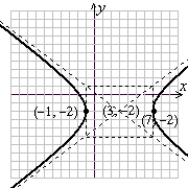
C)
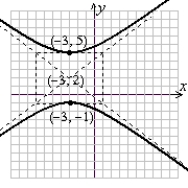
D)
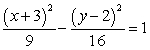
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
24
Sketch a complete graph of the equation, including asymptotes. Be sure to identify the center and vertices.
(x - 1)2 - 9(y - 2)2 = 9
(x - 1)2 - 9(y - 2)2 = 9

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
25
Use the following to answer questions :
y = x2 - 4x + 3
Find the vertex.
y = x2 - 4x + 3
Find the vertex.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
26
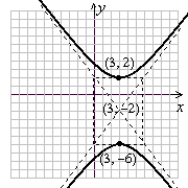
Graph the hyperbola. Label the vertices. 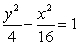
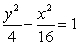

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
27
Sketch a complete graph of the equation, including asymptotes. Be sure to identify the center and vertices. 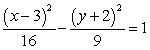
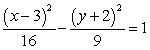

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
28
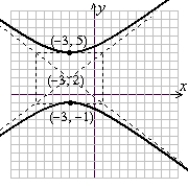
For the graph given, state the location of the vertices, the equation of the transverse axis, the location of the center, and the equation of the conjugate axis. 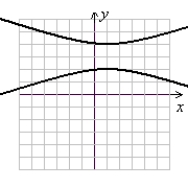 (Gridlines are spaced one unit apart.)
(Gridlines are spaced one unit apart.)
A) vertices: (1, 2), (1, 4); transverse axis: x = 3; center (1, 3); conjugate axis: y = 1
B) vertices: (1, 2), (1, 4); transverse axis: y = 3; center (1, 3); conjugate axis: x = 1
C) vertices: (1, 2), (1, 4); transverse axis: x = 1; center (1, 3); conjugate axis: y = 3
D) vertices: (1, 2), (1, 4); transverse axis: y = 1; center (1, 3); conjugate axis: x = 3
 (Gridlines are spaced one unit apart.)
(Gridlines are spaced one unit apart.)A) vertices: (1, 2), (1, 4); transverse axis: x = 3; center (1, 3); conjugate axis: y = 1
B) vertices: (1, 2), (1, 4); transverse axis: y = 3; center (1, 3); conjugate axis: x = 1
C) vertices: (1, 2), (1, 4); transverse axis: x = 1; center (1, 3); conjugate axis: y = 3
D) vertices: (1, 2), (1, 4); transverse axis: y = 1; center (1, 3); conjugate axis: x = 3

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
29
Classify the equation as that of a circle, ellipse, hyperbola, or none of the above. 9x2 + 9y2 - 18x + 72y + 72 = 0
A) Circle
B) Ellipse
C) Hyperbola
D) None of these
A) Circle
B) Ellipse
C) Hyperbola
D) None of these

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
30
Classify the equation as that of a circle, ellipse, hyperbola, or none of the above. 4x2 - 7y2 = 28
A) Circle
B) Ellipse
C) Hyperbola
D) None of these
A) Circle
B) Ellipse
C) Hyperbola
D) None of these

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
31
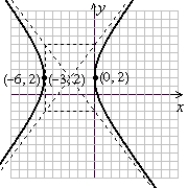
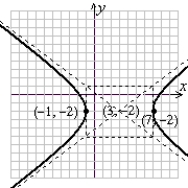
Sketch a complete graph of the equation, including asymptotes. Be sure to identify the center and vertices. 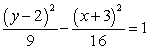
A)
B)
C)
D)
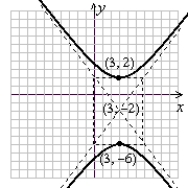
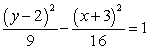
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
32
For the graph given, state
(a) the location of the vertices
(b) the equation of the transverse axis
(c) the location of the center
(d) the equation of the conjugate axis
Assume all coordinates are lattice points.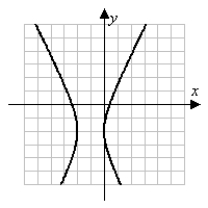 (Gridlines are spaced one unit apart.)
(Gridlines are spaced one unit apart.)
(a) the location of the vertices
(b) the equation of the transverse axis
(c) the location of the center
(d) the equation of the conjugate axis
Assume all coordinates are lattice points.
 (Gridlines are spaced one unit apart.)
(Gridlines are spaced one unit apart.)
Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
33
Sketch a complete graph of the equation, including asymptotes. Be sure to identify the center and vertices.
x2 - 9y2 - 6x - 36y - 36 = 0
x2 - 9y2 - 6x - 36y - 36 = 0

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
34
Sketch a complete graph of the equation, including asymptotes. Be sure to identify the center and vertices. 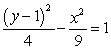
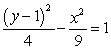

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
35
Graph the hyperbola. Label the vertices. 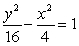
A)
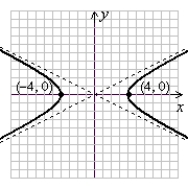
(Gridlines are spaced one unit apart.)
B)
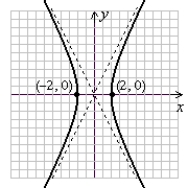
(Gridlines are spaced one unit apart.)
C)
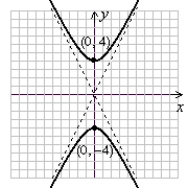
(Gridlines are spaced one unit apart.)
D)
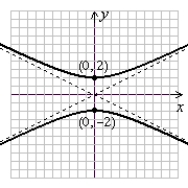
(Gridlines are spaced one unit apart.)
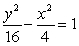
A)

(Gridlines are spaced one unit apart.)
B)

(Gridlines are spaced one unit apart.)
C)

(Gridlines are spaced one unit apart.)
D)

(Gridlines are spaced one unit apart.)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
36
Classify the equation as that of a circle, ellipse, hyperbola, or none of the above. 9x2 = -49y2 + 441
A) Circle
B) Ellipse
C) Hyperbola
D) None of these
A) Circle
B) Ellipse
C) Hyperbola
D) None of these

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
37
Sketch a complete graph of the equation, including asymptotes. Be sure to identify the center and vertices.
25y2 - 4x2 = 100
25y2 - 4x2 = 100

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
38
Classify the equation as that of a circle, ellipse, hyperbola, or none of the above. 8y2 - 4 = 5x2 + 36
A) Circle
B) Ellipse
C) Hyperbola
D) None of these
A) Circle
B) Ellipse
C) Hyperbola
D) None of these

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
39
Classify the equation as that of a circle, ellipse, hyperbola, or none of the above. -2x2 + -2y2= -20
A) Circle
B) Ellipse
C) Hyperbola
D) None of these
A) Circle
B) Ellipse
C) Hyperbola
D) None of these

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
40
Use the following to answer questions :
y = x2 - 4x + 3
Find the x- and y-intercepts (if they exist).
y = x2 - 4x + 3
Find the x- and y-intercepts (if they exist).

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
41
Use the following to answer questions :
x = -y2 + 6y - 8
Sketch the graph using symmetry and a few additional points.
A)
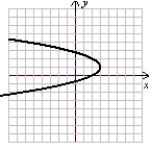
(Gridlines are spaced one unit apart.)
B)
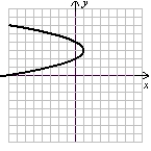
(Gridlines are spaced one unit apart.)
C)
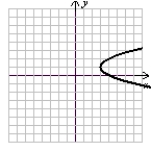
(Gridlines are spaced one unit apart.)
D)
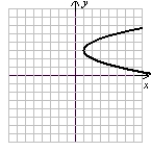
(Gridlines are spaced one unit apart.)
x = -y2 + 6y - 8
Sketch the graph using symmetry and a few additional points.
A)

(Gridlines are spaced one unit apart.)
B)

(Gridlines are spaced one unit apart.)
C)

(Gridlines are spaced one unit apart.)
D)

(Gridlines are spaced one unit apart.)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
42
Use the following to answer questions :
y = 2x2 - x - 3
Sketch the graph using symmetry and a few additional points or completing the square and shifting a parent function.
A)
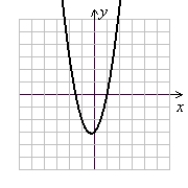
(Gridlines are spaced one unit apart.)
B)
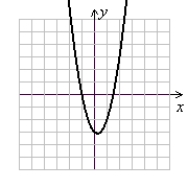
(Gridlines are spaced one unit apart.)
C)
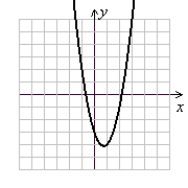
(Gridlines are spaced one unit apart.)
D)
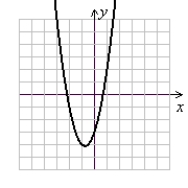
(Gridlines are spaced one unit apart.)
y = 2x2 - x - 3
Sketch the graph using symmetry and a few additional points or completing the square and shifting a parent function.
A)

(Gridlines are spaced one unit apart.)
B)

(Gridlines are spaced one unit apart.)
C)

(Gridlines are spaced one unit apart.)
D)

(Gridlines are spaced one unit apart.)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
43
Use the following to answer questions :
x = -y2 + 6y - 8
Find the x- and y-intercepts, if they exist.
A) x-intercepts: (2, 0), (4, 0); y-intercept: (0, -8)
B) x-intercept: (2, 0); y-intercepts: (0, -8), (0, 4)
C) x-intercept: (-8, 0); y-intercepts: (0, 2), (0, 4)
D) x-intercepts: none; y-intercept (0, -8)
x = -y2 + 6y - 8
Find the x- and y-intercepts, if they exist.
A) x-intercepts: (2, 0), (4, 0); y-intercept: (0, -8)
B) x-intercept: (2, 0); y-intercepts: (0, -8), (0, 4)
C) x-intercept: (-8, 0); y-intercepts: (0, 2), (0, 4)
D) x-intercepts: none; y-intercept (0, -8)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
44
(a) Sketch x = y2 + 4y + 3 using symmetry and shifts of a basic function.
(b) Find the x- and y-intercepts (if they exist).
(c) Find the vertex.
(d) State the domain and range of the relation.
(b) Find the x- and y-intercepts (if they exist).
(c) Find the vertex.
(d) State the domain and range of the relation.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
45
(a) Sketch x = y2 - 4y using symmetry and shifts of a basic function.
(b) Find the x- and y-intercepts (if they exist).
(c) Find the vertex.
(d) State the domain and range of the relation.
(b) Find the x- and y-intercepts (if they exist).
(c) Find the vertex.
(d) State the domain and range of the relation.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
46
Use the following to answer questions :
x2 = 28y
Find the directrix.
x2 = 28y
Find the directrix.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
47
Use the following to answer questions :
y2 = 36x
Find the directrix.
A) y = -8
B) y = 8
C) x = -8
D) x = 8
y2 = 36x
Find the directrix.
A) y = -8
B) y = 8
C) x = -8
D) x = 8

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
48
Use the following to answer questions :
x = y2 - 2y - 3
Find the vertex.
x = y2 - 2y - 3
Find the vertex.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
49
Use the following to answer questions :
x = y2 - 2y - 3
Find the x- and y-intercepts, if they exist.
x = y2 - 2y - 3
Find the x- and y-intercepts, if they exist.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
50
Sketch x = (y - 1)2 - 4 using symmetry and shifts of a basic function.
A)
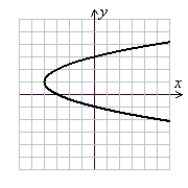
(Gridlines are spaced one unit apart.)
B)
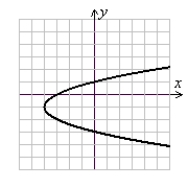
(Gridlines are spaced one unit apart.)
C)
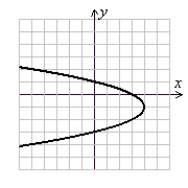
(Gridlines are spaced one unit apart.)
D)
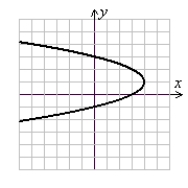
(Gridlines are spaced one unit apart.)
A)

(Gridlines are spaced one unit apart.)
B)

(Gridlines are spaced one unit apart.)
C)

(Gridlines are spaced one unit apart.)
D)

(Gridlines are spaced one unit apart.)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
51
Use the following to answer questions :
x2 = 28y
Find the vertex.
x2 = 28y
Find the vertex.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
52
Use the following to answer questions :
x = -y2 + 6y - 8
-State the domain and range.
A) x (- , 1]; y (- , )
B) x (- , ); y (- , 3]
C) x [3, ); y (- , )
D) x (- , ); y (- , )
x = -y2 + 6y - 8
-State the domain and range.
A) x (- , 1]; y (- , )
B) x (- , ); y (- , 3]
C) x [3, ); y (- , )
D) x (- , ); y (- , )

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
53
Find the vertex, focus, and directrix for the parabola given, then use this information to sketch a complete graph (illustrate these features).
y2 = -8x
y2 = -8x

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
54
Use the following to answer questions :
y = 2x2 - x - 3
Find the vertex.
A)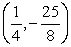
B)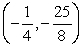
C)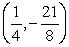
D)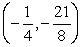
y = 2x2 - x - 3
Find the vertex.
A)
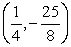
B)
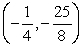
C)
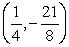
D)
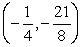

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
55
Use the following to answer questions :
x2 = 28y
Find the focus.
x2 = 28y
Find the focus.

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
56
Use the following to answer questions :
y2 = 36x
Find the focus.
A) (0, -6)
B) (0, -24)
C) (-6, 0)
D) (-24, 0)
y2 = 36x
Find the focus.
A) (0, -6)
B) (0, -24)
C) (-6, 0)
D) (-24, 0)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
57
Use the following to answer questions :
y = 2x2 - x - 3
-State the domain and range.
A) x (- , ); y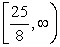
B) x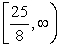 ; y (- , )
; y (- , )
C) x (- , ); y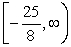
D) x (- , ); y (- , )
y = 2x2 - x - 3
-State the domain and range.
A) x (- , ); y
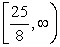
B) x
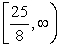 ; y (- , )
; y (- , )C) x (- , ); y
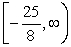
D) x (- , ); y (- , )

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
58
Use the following to answer questions :
x = -y2 + 6y - 8
Find the vertex.
A) (-80, -6)
B) (-8, 6)
C) (-35, -3)
D) (1, 3)
x = -y2 + 6y - 8
Find the vertex.
A) (-80, -6)
B) (-8, 6)
C) (-35, -3)
D) (1, 3)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
59
Use the following to answer questions :
y2 = 36x
Find the vertex.
A) (0, 0)
B) (0, -5)
C) (0, -20)
D) (-20, 0)
y2 = 36x
Find the vertex.
A) (0, 0)
B) (0, -5)
C) (0, -20)
D) (-20, 0)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
60
Identify each equation in the system as that of a line, parabola, circle, ellipse, or hyperbola, and solve the system by graphing. 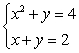
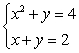

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
61
Solve using elimination. 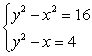
A) (4, 0), (5, -3), (-5, -3)
B) (-4, 0), (5, -3), (5, -3)
C) (-4, 0), (5, -3), (5, 3)
D) no solutions
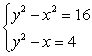
A) (4, 0), (5, -3), (-5, -3)
B) (-4, 0), (5, -3), (5, -3)
C) (-4, 0), (5, -3), (5, 3)
D) no solutions

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
62
List three alternate ways the point 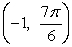 can be expressed in polar coordinates using r > 0, r < 0, and [-2 , 2 ).
can be expressed in polar coordinates using r > 0, r < 0, and [-2 , 2 ).
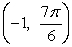 can be expressed in polar coordinates using r > 0, r < 0, and [-2 , 2 ).
can be expressed in polar coordinates using r > 0, r < 0, and [-2 , 2 ). 
Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
63
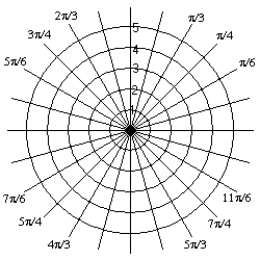
Plot the point 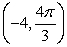 .
. 
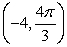 .
. 

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
64
Solve using the method of your choice. 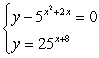
A) (4, 524)
B) (-4, 58)
C) (4, 524), (-4, 58)
D) (4, 524), (-4, -58)
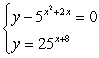
A) (4, 524)
B) (-4, 58)
C) (4, 524), (-4, 58)
D) (4, 524), (-4, -58)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
65
Solve the system of inequalities. 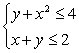
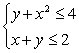

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
66
Convert from rectangular coordinates to polar coordinates. A diagram may help.
(8, -8)
(8, -8)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
67
Plot the point 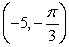 .
.
A)
B)
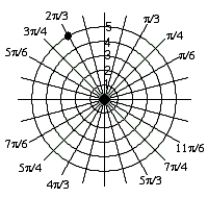
C)
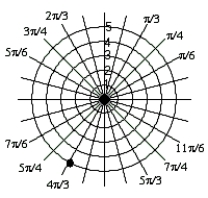
D)
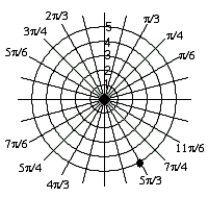
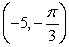 .
.A)

B)

C)

D)


Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
68
Identify each equation in the system as that of a line, parabola, circle, ellipse, or hyperbola, and solve the system by graphing. 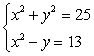
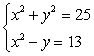

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
69
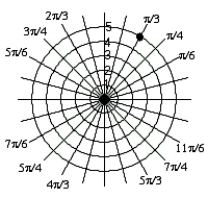
Express the point shown using polar coordinates with in radians, 0 < 2? and r > 0. 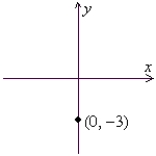


Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
70
Solve using elimination. 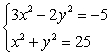
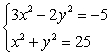

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
71
Solve using substitution. [Hint: Substitute for y2 (not x).] ![Solve using substitution. [Hint: Substitute for y<sup>2</sup> (not x).]](https://storage.examlex.com/TB3307/11ea7f29_501b_b102_9ecd_8389f20b8171_TB3307_00.jpg)
![Solve using substitution. [Hint: Substitute for y<sup>2</sup> (not x).]](https://storage.examlex.com/TB3307/11ea7f29_501b_b102_9ecd_8389f20b8171_TB3307_00.jpg)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
72
Convert from rectangular coordinates to polar coordinates. A diagram may help. 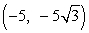
A)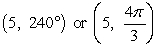
B)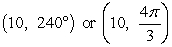
C)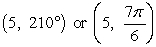
D)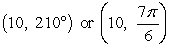
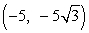
A)
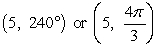
B)
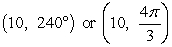
C)
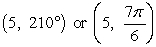
D)
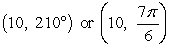

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
73
Plot the point 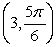 .
. 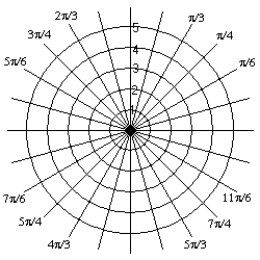
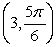 .
. 

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
74
Solve using substitution. 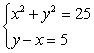
A) (0, 5), (5, 0)
B) (0, 5), (-5, 0)
C) (0, -5), (5, 0)
D) (0, -5), (-5, 0)
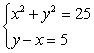
A) (0, 5), (5, 0)
B) (0, 5), (-5, 0)
C) (0, -5), (5, 0)
D) (0, -5), (-5, 0)

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
75
Solve the system of inequalities. 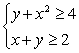
A)
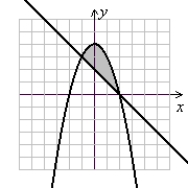
(Gridlines are spaced one unit apart.)
B)
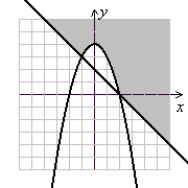
(Gridlines are spaced one unit apart.)
C)
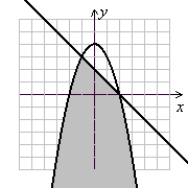
(Gridlines are spaced one unit apart.)
D) Ø
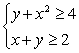
A)

(Gridlines are spaced one unit apart.)
B)

(Gridlines are spaced one unit apart.)
C)

(Gridlines are spaced one unit apart.)
D) Ø

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
76
Solve the system of inequalities. 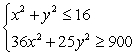
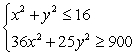

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
77
Solve the system of inequalities. 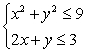
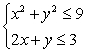

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
78
Solve using the method of your choice. 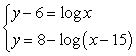
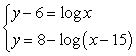

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
79
Solve the system of inequalities. 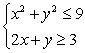
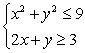

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck
80
Solve the system of inequalities. 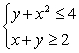
A)
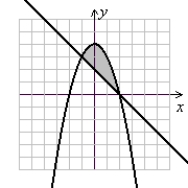
(Gridlines are spaced one unit apart.)
B)
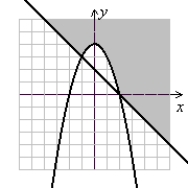
(Gridlines are spaced one unit apart.)
C)
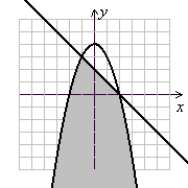
(Gridlines are spaced one unit apart.)
D) Ø
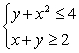
A)

(Gridlines are spaced one unit apart.)
B)

(Gridlines are spaced one unit apart.)
C)

(Gridlines are spaced one unit apart.)
D) Ø

Unlock Deck
Unlock for access to all 122 flashcards in this deck.
Unlock Deck
k this deck


