Deck 10: Additional Topics in Algebra
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/121
Play
Full screen (f)
Deck 10: Additional Topics in Algebra
1
Write out the first four terms in the sequence. 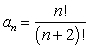
A)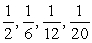
B)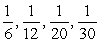
C)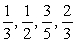
D)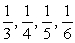
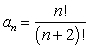
A)
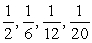
B)
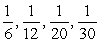
C)
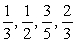
D)
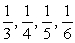
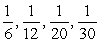
2
Expand and evaluate the series. 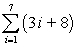
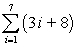
140
3
Use the following to answer questions :
14, 20, 26, 32, 38, . . .
Predict the next term for the sequence.
A) 55
B) 56
C) 57
D) 58
14, 20, 26, 32, 38, . . .
Predict the next term for the sequence.
A) 55
B) 56
C) 57
D) 58
57
4
Find the indicated term for the sequence. an = 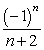 ; a19.
; a19.
A)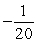
B)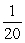
C)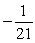
D)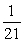
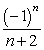 ; a19.
; a19.A)
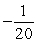
B)
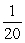
C)
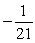
D)
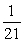

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
5
Write out the first four terms in the sequence. 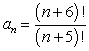
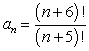

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
6
Simplify the factorial expression. 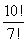
A)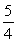
B) 5
C) 720
D) 5760
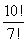
A)
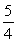
B) 5
C) 720
D) 5760

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
7
Use the following to answer questions :
10, 100, 1000, 10,000, 100,000, . . .
Find the general term for the sequence.
A) an = 10n
B) an = 10n
C) an = n10
D) an = 10n - 1
10, 100, 1000, 10,000, 100,000, . . .
Find the general term for the sequence.
A) an = 10n
B) an = 10n
C) an = n10
D) an = 10n - 1

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
8
Use the following to answer questions :
an = (-1)n (n + 1)
Find the 20th term.
A) 21
B) -21
C) 20
D) -20
an = (-1)n (n + 1)
Find the 20th term.
A) 21
B) -21
C) 20
D) -20

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
9
Find the first five terms of the recursive sequence. 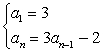
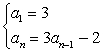

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
10
Simplify the factorial expression. 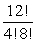
A) 495
B) 55
C)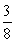
D)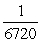
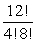
A) 495
B) 55
C)
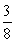
D)
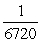

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
11
Find the indicated term for the sequence.
an =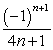 ; a10.
; a10.
an =
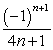 ; a10.
; a10.
Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
12
Expand and evaluate the series. 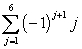
A) -3
B) -4
C) -5
D) -6
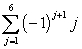
A) -3
B) -4
C) -5
D) -6

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
13
Use the following to answer questions :
14, 20, 26, 32, 38, . . .
Find the general term for the sequence.
A) an = n + 11
B) an = 5n + 7
C) an = -4n + 16
D) an = 4n + 8
14, 20, 26, 32, 38, . . .
Find the general term for the sequence.
A) an = n + 11
B) an = 5n + 7
C) an = -4n + 16
D) an = 4n + 8

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
14
Simplify the factorial expression. 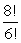
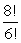

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
15
Find the partial sum S4 for the sequence. an = -4n + 5
A) -21
B) -20
C) -19
D) -18
A) -21
B) -20
C) -19
D) -18

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
16
(a) Find the first four terms for the nth term given.
(b) Find the 9th term.
an = 9n + 4
(b) Find the 9th term.
an = 9n + 4

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
17
Write the sum using sigma notation. Answers are not necessarily unique.
10 + 20 + 30 + 40 + 50 + 60
10 + 20 + 30 + 40 + 50 + 60

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
18
Simplify the factorial expression. 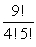
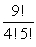

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
19
Use the following to answer questions :
an = (-1)n (n + 1)
Find the first four terms and write them as a list.
A) 1, -2, 3, -4
B) -1, 2, -3, 4
C) 2, -3, 4, -5
D) -2, 3, -4, 5
an = (-1)n (n + 1)
Find the first four terms and write them as a list.
A) 1, -2, 3, -4
B) -1, 2, -3, 4
C) 2, -3, 4, -5
D) -2, 3, -4, 5

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
20
Use the following to answer questions :
10, 100, 1000, 10,000, 100,000, . . .
Predict the next term for the sequence.
10, 100, 1000, 10,000, 100,000, . . .
Predict the next term for the sequence.

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
21
Find the number of terms in the series and then find the sum using the alternate formula. 11 + 19 + 27 + 35 + 43 + . . . + 163
A) n = 19; S20 = 1583
B) n = 19; S20 = 1591
C) n = 20; S20 = 1740
D) n = 21; S20 = 1911
A) n = 19; S20 = 1583
B) n = 19; S20 = 1591
C) n = 20; S20 = 1740
D) n = 21; S20 = 1911

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
22
Use the following to answer questions :
Kelly earns $8.80 per hour. Each year she receives a $0.80 hourly raise.
How much will Angie make the fifth year if she works 8 hr per day for 250 working days?
A) $19,400.00
B) $20,800.00
C) $22,200.00
D) $23,600.00
Kelly earns $8.80 per hour. Each year she receives a $0.80 hourly raise.
How much will Angie make the fifth year if she works 8 hr per day for 250 working days?
A) $19,400.00
B) $20,800.00
C) $22,200.00
D) $23,600.00

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
23
(a) Identify the first term a1 of the arithmetic sequence.
(b) Identify the common difference d.
(c) Write an expression for the general term an.
(d) Use the general term to find the 12th term of the sequence.
11, 14, 17, 20, 23, . . .
(b) Identify the common difference d.
(c) Write an expression for the general term an.
(d) Use the general term to find the 12th term of the sequence.
11, 14, 17, 20, 23, . . .

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
24
Evaluate the sum. Use the summation properties from Section 8.1. 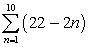
A) 112
B) 110
C) 108
D) 106
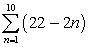
A) 112
B) 110
C) 108
D) 106

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
25
Find the number of terms n in an arithmetic sequence if a1 = 13, an = -95, and d = -6
A) 17
B) 18
C) 19
D) 20
A) 17
B) 18
C) 19
D) 20

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
26
Determine if the sequence given is arithmetic. If yes, name the common difference. -3, -6, -12, -18, -24, . . .
A) arithmetic; d = 2
B) arithmetic; d = 3
C) arithmetic; d = -3
D) not arithmetic
A) arithmetic; d = 2
B) arithmetic; d = 3
C) arithmetic; d = -3
D) not arithmetic

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
27
Use the following to answer questions :
Kelly earns $8.80 per hour. Each year she receives a $0.80 hourly raise.
List Felicia's hourly wage for the first 5 years.
Kelly earns $8.80 per hour. Each year she receives a $0.80 hourly raise.
List Felicia's hourly wage for the first 5 years.

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
28
Write the sum using sigma notation. Answers are not necessarily unique. 1 - 4 + 9 - 16 + 25
A)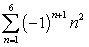
B)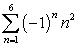
C)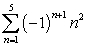
D)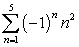
A)
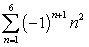
B)
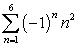
C)
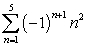
D)
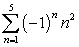

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
29
Write the first four terms of the arithmetic sequence with the given first term and common difference. a1 = 10, d = -2
A) -2, -12, -22, -32
B) -2, 8, 18, 28
C) 10, 12, 14, 16
D) 10, 8, 6, 4
A) -2, -12, -22, -32
B) -2, 8, 18, 28
C) 10, 12, 14, 16
D) 10, 8, 6, 4

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
30
Write the series in sigma notation. Simplify the series (if possible) before you begin. 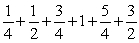
A)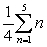
B)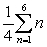
C)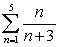
D)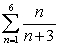
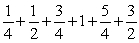
A)
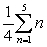
B)
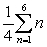
C)
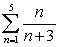
D)
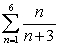

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
31
Write the series in sigma notation. Simplify the series (if possible) before you begin. 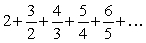
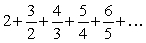

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
32
Find the common difference d and the value of a1 given a5 = -24, and a16 = -123.

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
33
Use the alternative formula for the nth partial sum to compute S15 for the sequence.
-18 + (-15.5) + (-13) + (-10.5) + (-8) + . . .
-18 + (-15.5) + (-13) + (-10.5) + (-8) + . . .

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
34
Find the sum of the first 20 multiples of 6.

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
35
Find a12 for an arithmetic sequence with a1 = 14 and d = -2.
A) -6
B) -8
C) -10
D) -12
A) -6
B) -8
C) -10
D) -12

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
36
Determine if the sequence given is arithmetic. If yes, name the common difference. 4, 6, 8, 10, 12, . . .
A) arithmetic; d = 2
B) arithmetic; d = -2
C) arithmetic; d = 4
D) not arithmetic
A) arithmetic; d = 2
B) arithmetic; d = -2
C) arithmetic; d = 4
D) not arithmetic

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
37
Write the first four terms of the arithmetic sequence with the given first term and common difference.
a1 = 3, d = 3
a1 = 3, d = 3

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
38
For the given general term an, write the sum S7 using sigma notation.
an = n + 9
an = n + 9

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
39
Jim deposits $15,000 in an account on January 1. Starting on January 2, he withdraws $100 each morning. Find the amount in his account on the evening of January 27. (Hint: For a1 = 15,000, the amount remaining 26 days later will be what term of the sequence?)
A) $12,700
B) $12,600
C) $12500
D) $12,400
A) $12,700
B) $12,600
C) $12500
D) $12,400

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
40
Evaluate the sum. 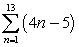
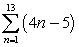

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
41
Use the following to answer questions :
an = 7n + 5
Find a4.
A) 22
B) 29
C) 36
D) 43
an = 7n + 5
Find a4.
A) 22
B) 29
C) 36
D) 43

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
42
Find the indicated sum. Use the summation properties from Section 8.1. Round your answer to 2 decimal places. 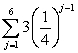
A) 3.96
B) 3.98
C) 4.00
D) 4.02
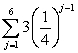
A) 3.96
B) 3.98
C) 4.00
D) 4.02

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
43
Determine if the sequence given is geometric. If yes, name the common ratio. 9, 4, -1, -6, -11, . . .
A) geometric; r = -5
B) geometric; r = 5
C) geometric; r = 9
D) not geometric
A) geometric; r = -5
B) geometric; r = 5
C) geometric; r = 9
D) not geometric

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
44
Use the following to answer questions :
A biologist finds that the population of a certain type of bacteria doubles each half-hour. An initial culture has 90 bacteria.
How long will it take for the number of bacteria to reach 245,760?
A) 5.5 hours
B) 6 hours
C) 6.5 hours
D) 7 hours
A biologist finds that the population of a certain type of bacteria doubles each half-hour. An initial culture has 90 bacteria.
How long will it take for the number of bacteria to reach 245,760?
A) 5.5 hours
B) 6 hours
C) 6.5 hours
D) 7 hours

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
45
Determine if the sequence given is geometric. If yes, name the common ratio. 4, -12, 36, -108, 324, . . .
A) geometric; r = 3
B) geometric; r = 4
C) geometric; r = -3
D) not geometric
A) geometric; r = 3
B) geometric; r = 4
C) geometric; r = -3
D) not geometric

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
46
Use the following to answer questions :
A biologist finds that the population of a certain type of bacteria doubles each half-hour. An initial culture has 90 bacteria.
What is the population after 5 hours?
A) 100
B) 200
C) 640
D) 20,480
A biologist finds that the population of a certain type of bacteria doubles each half-hour. An initial culture has 90 bacteria.
What is the population after 5 hours?
A) 100
B) 200
C) 640
D) 20,480

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
47
Find the number of terms n in the sequence. 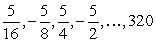
A) 9
B) 10
C) 11
D) 12
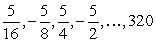
A) 9
B) 10
C) 11
D) 12

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
48
Find a6 for a geometric sequence with a1 = 3 and r = 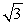 .
.
A)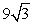
B) 27
C)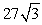
D) 81
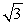 .
.A)
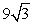
B) 27
C)
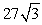
D) 81

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
49
Find the number of terms n in the sequence.
a1 = 3, an = 192, and r = 2.
a1 = 3, an = 192, and r = 2.

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
50
Use the following to answer questions :
an = 7n + 5
Find a5.
A) 7
B) 11
C) 15
D) 19
an = 7n + 5
Find a5.
A) 7
B) 11
C) 15
D) 19

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
51
Determine whether the infinite geometric series has a finite sum. If so, find the limiting value. 112 + 56 + 28 + . . .
A) S∞ = 224
B) S∞ = -224
C) S∞ = 56
D) no finite sum
A) S∞ = 224
B) S∞ = -224
C) S∞ = 56
D) no finite sum

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
52
Use the following to answer questions :
A geometric sequence has terms a3 = 576 and a6 = 243.
Find the common ratio r.
A)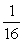
B)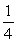
C)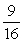
D)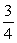
A geometric sequence has terms a3 = 576 and a6 = 243.
Find the common ratio r.
A)
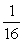
B)
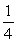
C)
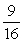
D)
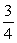

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
53
Write the first four terms of the geometric sequence given a1 = 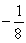 and r =
and r = 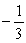 .
.
A)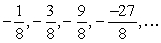
B)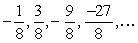
C)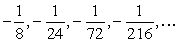
D)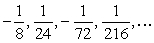
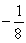 and r =
and r = 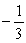 .
.A)
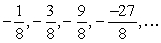
B)
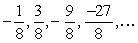
C)
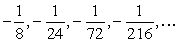
D)
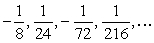

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
54
Use the following to answer questions :
A geometric sequence has terms a3 = 576 and a6 = 243.
Find the value of a1.
A) 256
B) 1024
C) 3072
D) 4096
A geometric sequence has terms a3 = 576 and a6 = 243.
Find the value of a1.
A) 256
B) 1024
C) 3072
D) 4096

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
55
Write the first four terms of the geometric sequence given a1 = 2 and r = -4.

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
56
Determine whether the infinite geometric series has a finite sum. If so, find the limiting value. 9 + 27 + 81 + 243 + 729 + . . .
A) S∞ =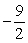
B) S∞ =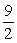
C) S∞ =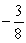
D) no finite sum
A) S∞ =
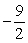
B) S∞ =
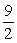
C) S∞ =
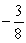
D) no finite sum

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
57
(a) Identify the first term a1 of the geometric sequence.
(b) Identify the common ratio r.
(c) Write an expression for the nth term an = a1rn-1.
(d) Use the expression for the nth term to find the 10th term.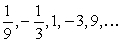
(b) Identify the common ratio r.
(c) Write an expression for the nth term an = a1rn-1.
(d) Use the expression for the nth term to find the 10th term.
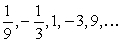

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
58
Find the sum S11 for a geometric sequence with a1 = 9 and r = -2.

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
59
Use the following to answer questions :
an = 7n + 5
Find ak.
A) ak = 7k + 3
B) ak = 7n + 3
C) ak = (7n + 3)k
D) ak = (7n + 3) + k
an = 7n + 5
Find ak.
A) ak = 7k + 3
B) ak = 7n + 3
C) ak = (7n + 3)k
D) ak = (7n + 3) + k

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
60
Determine whether the infinite geometric series has a finite sum. If so, find the limiting value. 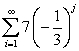
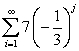

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
61
Use the following to answer questions :
an = 7n + 5
Find ak + 1.
A) ak + 1 = 7k - 1
B) ak + 1 = 7k + 3
C) ak + 1 = 7k + 4
D) ak + 1 = 7k + 5
an = 7n + 5
Find ak + 1.
A) ak + 1 = 7k - 1
B) ak + 1 = 7k + 3
C) ak + 1 = 7k + 4
D) ak + 1 = 7k + 5

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
62
Use mathematical induction to prove the indicated sum formula is true for all natural numbers n.
7 + 14 + 21 + 28 + . . . + 7n =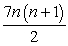 ;
;
an = 7n, Sn =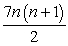
7 + 14 + 21 + 28 + . . . + 7n =
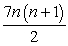 ;
;an = 7n, Sn =
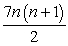

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
63
Find the value of 7P1 either by computing r factors of n! or by using the formula 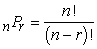 .
.
A) 0
B) 1
C) 7
D) 5040
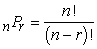 .
.A) 0
B) 1
C) 7
D) 5040

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
64
Use the following to answer questions :
A teacher is going to assign each student a 3-digit code using the digits 0 through 3.
How many codes are possible if repetitions are allowed?
A) 18
B) 120
C) 216
D) 125
A teacher is going to assign each student a 3-digit code using the digits 0 through 3.
How many codes are possible if repetitions are allowed?
A) 18
B) 120
C) 216
D) 125

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
65
For Sn = n(5n - 3), find S4, S5, Sk, and Sk + 1.

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
66
Use mathematical induction to prove that n2 - 13n is divisible by 2.

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
67
A Scrabble player has the six letters (A, A, E, E, N, N) in her rack. How many distinguishable, six-letter permutations can be formed?
A) 90
B) 240
C) 360
D) 720
A) 90
B) 240
C) 360
D) 720

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
68
Alex has 6 shirts, 6 pairs of pants, and 5 pairs of shoes. How many outfits can he wear?

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
69
How many different ways can 6 people stand in line at a cash register?

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
70
How many distinguishable permutations can be formed from the letters of the word assassin?

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
71
A coin is flipped three times. Draw a tree diagram illustrating all possible outcomes. How many elements are in the sample space?

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
72
Assuming the triplets are identical and cannot be told apart, how many distinguishable photographs can be taken of a family of 5, if they stand in a single row and there is one set of triplets?
A) 60
B) 40
C) 20
D) 120
A) 60
B) 40
C) 20
D) 120

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
73
Use mathematical induction to prove the indicated sum formula is true for all natural numbers n.
(-3) + (-1) + 1 + 3 + . . . + (2n - 5);
an = 2n - 5, Sn = n(n - 4)
(-3) + (-1) + 1 + 3 + . . . + (2n - 5);
an = 2n - 5, Sn = n(n - 4)

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
74
Find the value of 5P3 either by computing r factors of n! or by using the formula 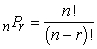 .
.
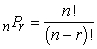 .
.
Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
75
Use the following to answer questions :
A teacher is going to assign each student a 3-digit code using the digits 0 through 3.
How many codes are possible if no repetitions are allowed?
A) 24
B) 125
C) 60
D) 64
A teacher is going to assign each student a 3-digit code using the digits 0 through 3.
How many codes are possible if no repetitions are allowed?
A) 24
B) 125
C) 60
D) 64

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
76
Use the following to answer questions :
A teacher is going to assign each student a 3-digit code using the digits 0 through 3.
How many codes are possible if repetitions are not allowed and the code must be less than 200 and divisible by 10?
A) 2
B) 24
C) 12
D) 3
A teacher is going to assign each student a 3-digit code using the digits 0 through 3.
How many codes are possible if repetitions are not allowed and the code must be less than 200 and divisible by 10?
A) 2
B) 24
C) 12
D) 3

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
77
A lock uses the numbers 0 through 12 for a four-number combination. How many different combinations are possible?
A) 48
B) 20,736
C) 28,561
D) 248,832
A) 48
B) 20,736
C) 28,561
D) 248,832

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
78
A club must elect a president, vice-president, and treasurer. In how many ways can the positions be filled if the club has 12 members?
A) 36
B) 220
C) 1320
D) 1728
A) 36
B) 220
C) 1320
D) 1728

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
79
Assuming the twins are identical and cannot be told apart, how many distinguishable photographs can be taken of a family of 4, if they stand in a single row and there is one set of twins?

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck
80
Use mathematical induction to prove the statement is true for all natural numbers n.
3n ≥ n + 2.
3n ≥ n + 2.

Unlock Deck
Unlock for access to all 121 flashcards in this deck.
Unlock Deck
k this deck


