Deck 13: Analysis of Variance and Experimental Design
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/113
Play
Full screen (f)
Deck 13: Analysis of Variance and Experimental Design
1
In order to determine whether or not the means of two populations are equal,
A)a t test must be performed
B)an analysis of variance must be performed
C)either a t test or an analysis of variance can be performed
D)a chi-square test must be performed
A)a t test must be performed
B)an analysis of variance must be performed
C)either a t test or an analysis of variance can be performed
D)a chi-square test must be performed
C
2
In ANOVA,which of the following is not affected by whether or not the population means are equal?
A)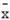
B)between-samples estimate of 2
C)within-samples estimate of 2
D)None of these alternatives is correct.
A)
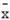
B)between-samples estimate of 2
C)within-samples estimate of 2
D)None of these alternatives is correct.
within-samples estimate of 2
3
In factorial designs,the response produced when the treatments of one factor interact with the treatments of another in influencing the response variable is known as
A)main effect
B)replication
C)interaction
D)None of these alternatives is correct.
A)main effect
B)replication
C)interaction
D)None of these alternatives is correct.
C
4
The required condition for using an ANOVA procedure on data from several populations is that the
A)the selected samples are dependent on each other
B)sampled populations are all uniform
C)sampled populations have equal variances
D)sampled populations have equal means
A)the selected samples are dependent on each other
B)sampled populations are all uniform
C)sampled populations have equal variances
D)sampled populations have equal means

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
5
The critical F value with 6 numerator and 60 denominator degrees of freedom at = .05 is
A)3.74
B)2.25
C)2.37
D)1.96
A)3.74
B)2.25
C)2.37
D)1.96

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
6
An ANOVA procedure is used for data that was obtained from four sample groups each comprised of five observations.The degrees of freedom for the critical value of F are
A)3 and 20
B)3 and 16
C)4 and 17
D)3 and 19
A)3 and 20
B)3 and 16
C)4 and 17
D)3 and 19

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
7
When an analysis of variance is performed on samples drawn from K populations,the mean square between treatments (MSTR)is
A)SSTR/nT
B)SSTR/(nT - 1)
C)SSTR/K
D)SSTR/(K - 1)
A)SSTR/nT
B)SSTR/(nT - 1)
C)SSTR/K
D)SSTR/(K - 1)

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
8
In an analysis of variance where the total sample size for the experiment is nT and the number of populations is K,the mean square within treatments is
A)SSE/(nT - K)
B)SSTR/(nT - K)
C)SSE/(K - 1)
D)SSE/K
A)SSE/(nT - K)
B)SSTR/(nT - K)
C)SSE/(K - 1)
D)SSE/K

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
9
An experimental design where the experimental units are randomly assigned to the treatments is known as
A)factor block design
B)random factor design
C)completely randomized design
D)None of these alternatives is correct.
A)factor block design
B)random factor design
C)completely randomized design
D)None of these alternatives is correct.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
10
A term that means the same as the term "variable" in an ANOVA procedure is
A)factor
B)treatment
C)replication
D)variance within
A)factor
B)treatment
C)replication
D)variance within

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
11
The variable of interest in an ANOVA procedure is called
A)a partition
B)a treatment
C)either a partition or a treatment
D)a factor
A)a partition
B)a treatment
C)either a partition or a treatment
D)a factor

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
12
In an analysis of variance problem involving 3 treatments and 10 observations per treatment,SSE = 399.6.The MSE for this situation is
A)133.2
B)13.32
C)14.8
D)30.0
A)133.2
B)13.32
C)14.8
D)30.0

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
13
The F ratio in a completely randomized ANOVA is the ratio of
A)MSTR/MSE
B)MST/MSE
C)MSE/MSTR
D)MSE/MST
A)MSTR/MSE
B)MST/MSE
C)MSE/MSTR
D)MSE/MST

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
14
The mean square is the sum of squares divided by
A)the total number of observations
B)its corresponding degrees of freedom
C)its corresponding degrees of freedom minus one
D)None of these alternatives is correct.
A)the total number of observations
B)its corresponding degrees of freedom
C)its corresponding degrees of freedom minus one
D)None of these alternatives is correct.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
15
In the analysis of variance procedure (ANOVA),"factor" refers to
A)the dependent variable
B)the independent variable
C)different levels of a treatment
D)the critical value of F
A)the dependent variable
B)the independent variable
C)different levels of a treatment
D)the critical value of F

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
16
In the ANOVA,treatment refers to
A)experimental units
B)different levels of a factor
C)the dependent variable
D)applying antibiotic to a wound
A)experimental units
B)different levels of a factor
C)the dependent variable
D)applying antibiotic to a wound

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
17
The number of times each experimental condition is observed in a factorial design is known as
A)partition
B)replication
C)experimental condition
D)factor
A)partition
B)replication
C)experimental condition
D)factor

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
18
The ANOVA procedure is a statistical approach for determining whether or not
A)the means of two samples are equal
B)the means of two or more samples are equal
C)the means of more than two samples are equal
D)the means of two or more populations are equal
A)the means of two samples are equal
B)the means of two or more samples are equal
C)the means of more than two samples are equal
D)the means of two or more populations are equal

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
19
An ANOVA procedure is applied to data obtained from 6 samples where each sample contains 20 observations.The degrees of freedom for the critical value of F are
A)6 numerator and 20 denominator degrees of freedom
B)5 numerator and 20 denominator degrees of freedom
C)5 numerator and 114 denominator degrees of freedom
D)6 numerator and 20 denominator degrees of freedom
A)6 numerator and 20 denominator degrees of freedom
B)5 numerator and 20 denominator degrees of freedom
C)5 numerator and 114 denominator degrees of freedom
D)6 numerator and 20 denominator degrees of freedom

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
20
In an analysis of variance problem if SST = 120 and SSTR = 80,then SSE is
A)200
B)40
C)80
D)120
A)200
B)40
C)80
D)120

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
21
Exhibit 13-2
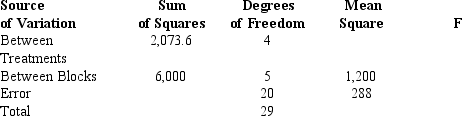
Refer to Exhibit 13-2.The mean square between treatments equals
A)288
B)518.4
C)1,200
D)8,294.4

Refer to Exhibit 13-2.The mean square between treatments equals
A)288
B)518.4
C)1,200
D)8,294.4

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
22
An ANOVA procedure is used for data obtained from five populations.five samples,each comprised of 20 observations,were taken from the five populations.The numerator and denominator (respectively)degrees of freedom for the critical value of F are
A)5 and 20
B)4 and 20
C)4 and 99
D)4 and 95
A)5 and 20
B)4 and 20
C)4 and 99
D)4 and 95

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
23
In a completely randomized design involving three treatments,the following information is provided:
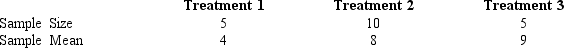
The overall mean for all the treatments is
A)7.00
B)6.67
C)7.25
D)4.89
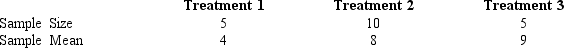
The overall mean for all the treatments is
A)7.00
B)6.67
C)7.25
D)4.89

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
24
The critical F value with 8 numerator and 29 denominator degrees of freedom at = 0.01 is
A)2.28
B)3.20
C)3.33
D)3.64
A)2.28
B)3.20
C)3.33
D)3.64

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
25
In an analysis of variance,one estimate of 2 is based upon the differences between the treatment means and the
A)means of each sample
B)overall sample mean
C)sum of observations
D)populations have equal means
A)means of each sample
B)overall sample mean
C)sum of observations
D)populations have equal means

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
26
Exhibit 13-2

Refer to Exhibit 13-2.The null hypothesis is to be tested at the 5% level of significance.The p-value is
A)greater than 0.10
B)between 0.10 to 0.05
C)between 0.05 to 0.025
D)between 0.025 to 0.01

Refer to Exhibit 13-2.The null hypothesis is to be tested at the 5% level of significance.The p-value is
A)greater than 0.10
B)between 0.10 to 0.05
C)between 0.05 to 0.025
D)between 0.025 to 0.01

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
27
Exhibit 13-2

Refer to Exhibit 13-2.The sum of squares due to error equals
A)14.4
B)2,073.6
C)5,760
D)6,000

Refer to Exhibit 13-2.The sum of squares due to error equals
A)14.4
B)2,073.6
C)5,760
D)6,000

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
28
Exhibit 13-1
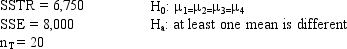
Refer to Exhibit 13-1.The mean square between treatments (MSTR)equals
A)400
B)500
C)1,687.5
D)2,250
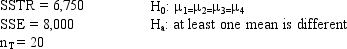
Refer to Exhibit 13-1.The mean square between treatments (MSTR)equals
A)400
B)500
C)1,687.5
D)2,250

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
29
In a completely randomized design involving four treatments,the following information is provided.
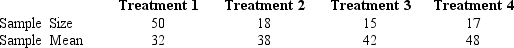
The overall mean (the grand mean)for all treatments is
A)40.0
B)37.3
C)48.0
D)37.0
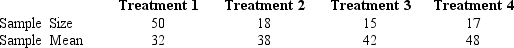
The overall mean (the grand mean)for all treatments is
A)40.0
B)37.3
C)48.0
D)37.0

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
30
Exhibit 13-2

Refer to Exhibit 13-2.The null hypothesis
A)should be rejected
B)should not be rejected
C)should be revised
D)None of these alternatives is correct.

Refer to Exhibit 13-2.The null hypothesis
A)should be rejected
B)should not be rejected
C)should be revised
D)None of these alternatives is correct.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
31
Which of the following is not a required assumption for the analysis of variance?
A)The random variable of interest for each population has a normal probability distribution.
B)The variance associated with the random variable must be the same for each population.
C)At least 2 populations are under consideration.
D)Populations have equal means.
A)The random variable of interest for each population has a normal probability distribution.
B)The variance associated with the random variable must be the same for each population.
C)At least 2 populations are under consideration.
D)Populations have equal means.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
32
An experimental design that permits statistical conclusions about two or more factors is a
A)randomized block design
B)factorial design
C)completely randomized design
D)randomized design
A)randomized block design
B)factorial design
C)completely randomized design
D)randomized design

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
33
The process of allocating the total sum of squares and degrees of freedom is called
A)factoring
B)blocking
C)replicating
D)partitioning
A)factoring
B)blocking
C)replicating
D)partitioning

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
34
An ANOVA procedure is used for data obtained from four populations.Four samples,each comprised of 30 observations,were taken from the four populations.The numerator and denominator (respectively)degrees of freedom for the critical value of F are
A)3 and 30
B)4 and 30
C)3 and 119
D)3 and 116
A)3 and 30
B)4 and 30
C)3 and 119
D)3 and 116

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
35
Exhibit 13-1
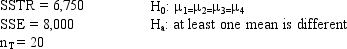
Refer to Exhibit 13-1.The null hypothesis is to be tested at the 5% level of significance.The p-value is
A)less than .01
B)between .01 and .025
C)between .025 and .05
D)between .05 and .10
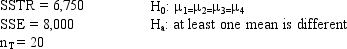
Refer to Exhibit 13-1.The null hypothesis is to be tested at the 5% level of significance.The p-value is
A)less than .01
B)between .01 and .025
C)between .025 and .05
D)between .05 and .10

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
36
Exhibit 13-2

-Refer to Exhibit 13-2.The null hypothesis for this ANOVA problem is
A) 1= 2= 3= 4
B) 1= 2= 3= 4= 5
C) 1= 2= 3= 4= 5= 6
D) 1= 2= ...= 20

-Refer to Exhibit 13-2.The null hypothesis for this ANOVA problem is
A) 1= 2= 3= 4
B) 1= 2= 3= 4= 5
C) 1= 2= 3= 4= 5= 6
D) 1= 2= ...= 20

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
37
Exhibit 13-1
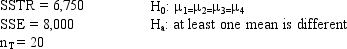
Refer to Exhibit 13-1.The test statistic to test the null hypothesis equals
A)0.22
B)0.84
C)4.22
D)4.5
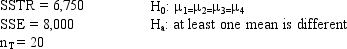
Refer to Exhibit 13-1.The test statistic to test the null hypothesis equals
A)0.22
B)0.84
C)4.22
D)4.5

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
38
Exhibit 13-2

Refer to Exhibit 13-2.The test statistic to test the null hypothesis equals
A)0.432
B)1.8
C)4.17
D)28.8

Refer to Exhibit 13-2.The test statistic to test the null hypothesis equals
A)0.432
B)1.8
C)4.17
D)28.8

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
39
Exhibit 13-1
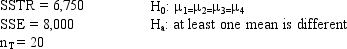
Refer to Exhibit 13-1.The null hypothesis
A)should be rejected
B)should not be rejected
C)was designed incorrectly
D)None of these alternatives is correct.
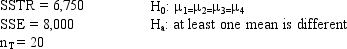
Refer to Exhibit 13-1.The null hypothesis
A)should be rejected
B)should not be rejected
C)was designed incorrectly
D)None of these alternatives is correct.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
40
Exhibit 13-1
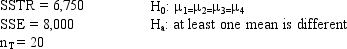
Refer to Exhibit 13-1.The mean square within treatments (MSE)equals
A)400
B)500
C)1,687.5
D)2,250
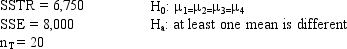
Refer to Exhibit 13-1.The mean square within treatments (MSE)equals
A)400
B)500
C)1,687.5
D)2,250

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
41
Exhibit 13-6
Part of an ANOVA table is shown below.

Refer to Exhibit 13-6.The number of degrees of freedom corresponding to between treatments is
A)18
B)2
C)4
D)3
Part of an ANOVA table is shown below.

Refer to Exhibit 13-6.The number of degrees of freedom corresponding to between treatments is
A)18
B)2
C)4
D)3

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
42
Exhibit 13-3
To test whether or not there is a difference between treatments A,B,and C,a sample of 12 observations has been randomly assigned to the 3 treatments.You are given the results below.
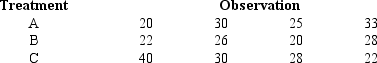
Refer to Exhibit 13-3.The mean square between treatments (MSTR)equals
A)1.872
B)5.86
C)34
D)36
To test whether or not there is a difference between treatments A,B,and C,a sample of 12 observations has been randomly assigned to the 3 treatments.You are given the results below.
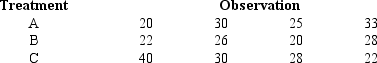
Refer to Exhibit 13-3.The mean square between treatments (MSTR)equals
A)1.872
B)5.86
C)34
D)36

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
43
Exhibit 13-3
To test whether or not there is a difference between treatments A,B,and C,a sample of 12 observations has been randomly assigned to the 3 treatments.You are given the results below.
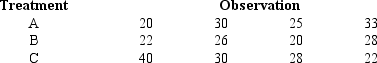
Refer to Exhibit 13-3.The test statistic to test the null hypothesis equals
A)0.944
B)1.059
C)3.13
D)19.231
To test whether or not there is a difference between treatments A,B,and C,a sample of 12 observations has been randomly assigned to the 3 treatments.You are given the results below.
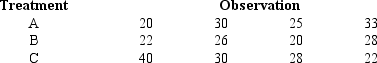
Refer to Exhibit 13-3.The test statistic to test the null hypothesis equals
A)0.944
B)1.059
C)3.13
D)19.231

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
44
Exhibit 13-5
Part of an ANOVA table is shown below.
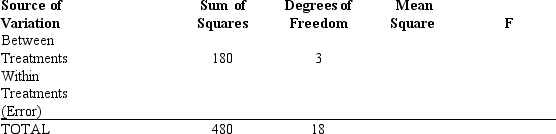
Refer to Exhibit 13-5.The mean square between treatments (MSTR)is
A)20
B)60
C)300
D)15
Part of an ANOVA table is shown below.

Refer to Exhibit 13-5.The mean square between treatments (MSTR)is
A)20
B)60
C)300
D)15

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
45
Exhibit 13-4
In a completely randomized experimental design involving five treatments,13 observations were recorded for each of the five treatments (a total of 65 observations).The following information is provided.
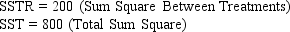
Refer to Exhibit 13-4.The sum of squares within treatments (SSE)is
A)1,000
B)600
C)200
D)1,600
In a completely randomized experimental design involving five treatments,13 observations were recorded for each of the five treatments (a total of 65 observations).The following information is provided.
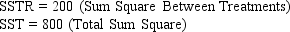
Refer to Exhibit 13-4.The sum of squares within treatments (SSE)is
A)1,000
B)600
C)200
D)1,600

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
46
Exhibit 13-3
To test whether or not there is a difference between treatments A,B,and C,a sample of 12 observations has been randomly assigned to the 3 treatments.You are given the results below.
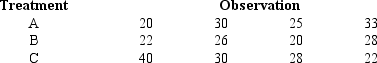
Refer to Exhibit 13-3.The null hypothesis is to be tested at the 1% level of significance.The p-value is
A)greater than 0.1
B)between 0.1 to 0.05
C)between 0.05 to 0.025
D)between 0.025 to 0.01
To test whether or not there is a difference between treatments A,B,and C,a sample of 12 observations has been randomly assigned to the 3 treatments.You are given the results below.
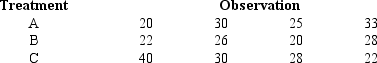
Refer to Exhibit 13-3.The null hypothesis is to be tested at the 1% level of significance.The p-value is
A)greater than 0.1
B)between 0.1 to 0.05
C)between 0.05 to 0.025
D)between 0.025 to 0.01

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
47
Exhibit 13-4
In a completely randomized experimental design involving five treatments,13 observations were recorded for each of the five treatments (a total of 65 observations).The following information is provided.
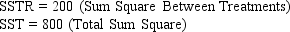
Refer to Exhibit 13-4.If at 95% confidence we want to determine whether or not the means of the five populations are equal,the p-value is
A)between 0.05 to 0.10
B)between 0.025 to 0.05
C)between 0.01 to 0.025
D)less than 0.01
In a completely randomized experimental design involving five treatments,13 observations were recorded for each of the five treatments (a total of 65 observations).The following information is provided.
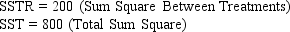
Refer to Exhibit 13-4.If at 95% confidence we want to determine whether or not the means of the five populations are equal,the p-value is
A)between 0.05 to 0.10
B)between 0.025 to 0.05
C)between 0.01 to 0.025
D)less than 0.01

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
48
Exhibit 13-4
In a completely randomized experimental design involving five treatments,13 observations were recorded for each of the five treatments (a total of 65 observations).The following information is provided.
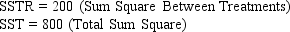
Refer to Exhibit 13-4.The number of degrees of freedom corresponding to within treatments is
A)60
B)59
C)5
D)4
In a completely randomized experimental design involving five treatments,13 observations were recorded for each of the five treatments (a total of 65 observations).The following information is provided.
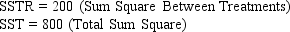
Refer to Exhibit 13-4.The number of degrees of freedom corresponding to within treatments is
A)60
B)59
C)5
D)4

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
49
Exhibit 13-5
Part of an ANOVA table is shown below.

Refer to Exhibit 13-5.The mean square within treatments (MSE)is
A)60
B)15
C)300
D)20
Part of an ANOVA table is shown below.

Refer to Exhibit 13-5.The mean square within treatments (MSE)is
A)60
B)15
C)300
D)20

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
50
Exhibit 13-6
Part of an ANOVA table is shown below.

Refer to Exhibit 13-6.The number of degrees of freedom corresponding to within treatments is
A)22
B)4
C)5
D)18
Part of an ANOVA table is shown below.

Refer to Exhibit 13-6.The number of degrees of freedom corresponding to within treatments is
A)22
B)4
C)5
D)18

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
51
Exhibit 13-5
Part of an ANOVA table is shown below.

Refer to Exhibit 13-5.If at 95% confidence,we want to determine whether or not the means of the populations are equal,the p-value is
A)between 0.01 to 0.025
B)between 0.025 to 0.05
C)between 0.05 to 0.1
D)greater than 0.1
Part of an ANOVA table is shown below.

Refer to Exhibit 13-5.If at 95% confidence,we want to determine whether or not the means of the populations are equal,the p-value is
A)between 0.01 to 0.025
B)between 0.025 to 0.05
C)between 0.05 to 0.1
D)greater than 0.1

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
52
Exhibit 13-4
In a completely randomized experimental design involving five treatments,13 observations were recorded for each of the five treatments (a total of 65 observations).The following information is provided.
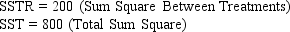
Refer to Exhibit 13-4.The mean square between treatments (MSTR)is
A)3.34
B)10.00
C)50.00
D)12.00
In a completely randomized experimental design involving five treatments,13 observations were recorded for each of the five treatments (a total of 65 observations).The following information is provided.
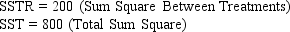
Refer to Exhibit 13-4.The mean square between treatments (MSTR)is
A)3.34
B)10.00
C)50.00
D)12.00

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
53
Exhibit 13-3
To test whether or not there is a difference between treatments A,B,and C,a sample of 12 observations has been randomly assigned to the 3 treatments.You are given the results below.
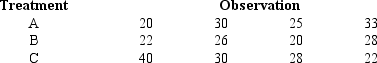
Refer to Exhibit 13-3.The null hypothesis
A)should be rejected
B)should not be rejected
C)should be revised
D)None of these alternatives is correct.
To test whether or not there is a difference between treatments A,B,and C,a sample of 12 observations has been randomly assigned to the 3 treatments.You are given the results below.
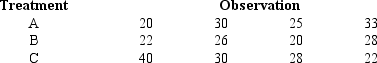
Refer to Exhibit 13-3.The null hypothesis
A)should be rejected
B)should not be rejected
C)should be revised
D)None of these alternatives is correct.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
54
Exhibit 13-5
Part of an ANOVA table is shown below.

Refer to Exhibit 13-5.The test statistic is
A)2.25
B)6
C)2.67
D)3
Part of an ANOVA table is shown below.

Refer to Exhibit 13-5.The test statistic is
A)2.25
B)6
C)2.67
D)3

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
55
Exhibit 13-4
In a completely randomized experimental design involving five treatments,13 observations were recorded for each of the five treatments (a total of 65 observations).The following information is provided.
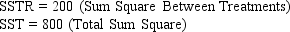
Refer to Exhibit 13-4.The test statistic is
A)0.2
B)5.0
C)3.75
D)15
In a completely randomized experimental design involving five treatments,13 observations were recorded for each of the five treatments (a total of 65 observations).The following information is provided.
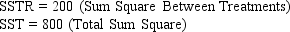
Refer to Exhibit 13-4.The test statistic is
A)0.2
B)5.0
C)3.75
D)15

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
56
Exhibit 13-3
To test whether or not there is a difference between treatments A,B,and C,a sample of 12 observations has been randomly assigned to the 3 treatments.You are given the results below.
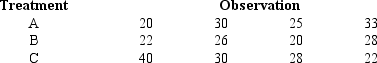
-Refer to Exhibit 13-3.The null hypothesis for this ANOVA problem is
A) 1= 2
B) 1= 2= 3
C) 1= 2= 3= 4
D) 1= 2= ...= 12
To test whether or not there is a difference between treatments A,B,and C,a sample of 12 observations has been randomly assigned to the 3 treatments.You are given the results below.
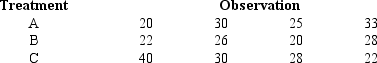
-Refer to Exhibit 13-3.The null hypothesis for this ANOVA problem is
A) 1= 2
B) 1= 2= 3
C) 1= 2= 3= 4
D) 1= 2= ...= 12

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
57
Exhibit 13-4
In a completely randomized experimental design involving five treatments,13 observations were recorded for each of the five treatments (a total of 65 observations).The following information is provided.
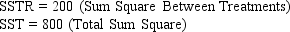
Refer to Exhibit 13-4.The number of degrees of freedom corresponding to between treatments is
A)60
B)59
C)5
D)4
In a completely randomized experimental design involving five treatments,13 observations were recorded for each of the five treatments (a total of 65 observations).The following information is provided.
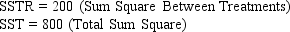
Refer to Exhibit 13-4.The number of degrees of freedom corresponding to between treatments is
A)60
B)59
C)5
D)4

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
58
Exhibit 13-6
Part of an ANOVA table is shown below.

Refer to Exhibit 13-6.The mean square between treatments (MSTR)is
A)36
B)16
C)64
D)15
Part of an ANOVA table is shown below.

Refer to Exhibit 13-6.The mean square between treatments (MSTR)is
A)36
B)16
C)64
D)15

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
59
Exhibit 13-4
In a completely randomized experimental design involving five treatments,13 observations were recorded for each of the five treatments (a total of 65 observations).The following information is provided.
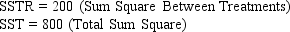
Refer to Exhibit 13-4.The mean square within treatments (MSE)is
A)50
B)10
C)200
D)600
In a completely randomized experimental design involving five treatments,13 observations were recorded for each of the five treatments (a total of 65 observations).The following information is provided.
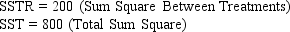
Refer to Exhibit 13-4.The mean square within treatments (MSE)is
A)50
B)10
C)200
D)600

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
60
Exhibit 13-3
To test whether or not there is a difference between treatments A,B,and C,a sample of 12 observations has been randomly assigned to the 3 treatments.You are given the results below.
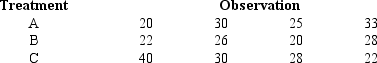
Refer to Exhibit 13-3.The mean square within treatments (MSE)equals
A)1.872
B)5.86
C)34
D)36
To test whether or not there is a difference between treatments A,B,and C,a sample of 12 observations has been randomly assigned to the 3 treatments.You are given the results below.
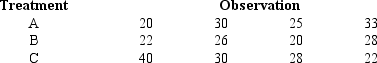
Refer to Exhibit 13-3.The mean square within treatments (MSE)equals
A)1.872
B)5.86
C)34
D)36

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
61
Random samples were selected from three populations.The data obtained are shown below.Please note that the sample sizes are not equal.

a.Compute the overall mean.
b.At 95% confidence,test to see if there is a significant difference among the means.

a.Compute the overall mean.
b.At 95% confidence,test to see if there is a significant difference among the means.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
62
Information regarding the starting salaries (in $1,000)of samples of students in four different majors is given below.
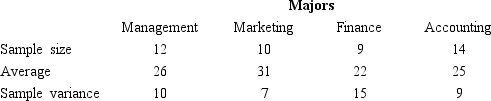
a.Compute the overall sample mean.
b.Set up the ANOVA table for this problem including the test statistic.
c.At 95% confidence,determine the critical value of F.
d.Using the critical value approach,test to determine whether there is a significant difference in the means of the three populations.
e.Determine the p-value and use it for the test.
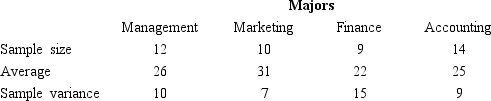
a.Compute the overall sample mean.
b.Set up the ANOVA table for this problem including the test statistic.
c.At 95% confidence,determine the critical value of F.
d.Using the critical value approach,test to determine whether there is a significant difference in the means of the three populations.
e.Determine the p-value and use it for the test.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
63
Exhibit 13-7
The following is part of an ANOVA table that was obtained from data regarding three treatments and a total of 15 observations.

Refer to Exhibit 13-7.The conclusion of the test is that the means
A)are equal
B)may be equal
C)are not equal
D)None of these alternatives is correct.
The following is part of an ANOVA table that was obtained from data regarding three treatments and a total of 15 observations.

Refer to Exhibit 13-7.The conclusion of the test is that the means
A)are equal
B)may be equal
C)are not equal
D)None of these alternatives is correct.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
64
In order to compare the life expectancies of three different brands of printers,eight printers of each brand were randomly selected.Information regarding the three brands is shown below.
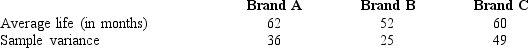
a.Compute the overall mean.
b.State the null and alternative hypotheses to be tested.
c.Show the complete ANOVA table for this test including the test statistic.
d.The null hypothesis is to be tested at 95% confidence.Determine the critical value for this test.What do you conclude?
e.Determine the p-value and use it for the test.
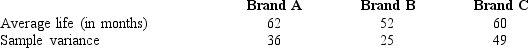
a.Compute the overall mean.
b.State the null and alternative hypotheses to be tested.
c.Show the complete ANOVA table for this test including the test statistic.
d.The null hypothesis is to be tested at 95% confidence.Determine the critical value for this test.What do you conclude?
e.Determine the p-value and use it for the test.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
65
Exhibit 13-6
Part of an ANOVA table is shown below.

Refer to Exhibit 13-6.The conclusion of the test is that the means
A)are equal
B)may be equal
C)are not equal
D)None of these alternatives is correct.
Part of an ANOVA table is shown below.

Refer to Exhibit 13-6.The conclusion of the test is that the means
A)are equal
B)may be equal
C)are not equal
D)None of these alternatives is correct.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
66
Three universities administer the same comprehensive examination to the recipients of MS degrees in psychology.From each institution,a random sample of MS recipients was selected,and these recipients were then given the exam.The following table shows the scores of the students from each university.Note that the sample sizes are not equal.
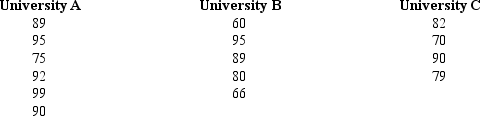
a.Compute the overall mean.
b.At = 0.01,test to see if there is any significant difference in the average scores of the students from the three universities.Use both the critical value and p-value approaches.

a.Compute the overall mean.
b.At = 0.01,test to see if there is any significant difference in the average scores of the students from the three universities.Use both the critical value and p-value approaches.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
67
Random samples were selected from three populations.The data obtained are shown below.Please note that the sample sizes are not equal.

a.Compute the overall mean.
b.At 95% confidence using the critical value and p-value approach,test to see if there is a significant difference among the means.

a.Compute the overall mean.
b.At 95% confidence using the critical value and p-value approach,test to see if there is a significant difference among the means.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
68
Exhibit 13-7
The following is part of an ANOVA table that was obtained from data regarding three treatments and a total of 15 observations.

Refer to Exhibit 13-7.The number of degrees of freedom corresponding to within treatments is
A)12
B)2
C)3
D)15
The following is part of an ANOVA table that was obtained from data regarding three treatments and a total of 15 observations.

Refer to Exhibit 13-7.The number of degrees of freedom corresponding to within treatments is
A)12
B)2
C)3
D)15

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
69
Exhibit 13-7
The following is part of an ANOVA table that was obtained from data regarding three treatments and a total of 15 observations.

Refer to Exhibit 13-7.The computed test statistics is
A)32
B)8
C)0.667
D)4
The following is part of an ANOVA table that was obtained from data regarding three treatments and a total of 15 observations.

Refer to Exhibit 13-7.The computed test statistics is
A)32
B)8
C)0.667
D)4

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
70
The test scores for selected samples of sociology students who took the course from three different instructors are shown below.
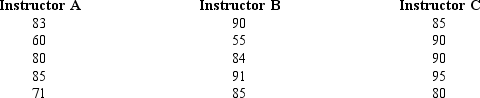
At = 0.05,test to see if there is a significant difference among the averages of the three groups.Use both the critical value and p-value approaches.

At = 0.05,test to see if there is a significant difference among the averages of the three groups.Use both the critical value and p-value approaches.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
71
Guitars R.US has three stores located in three different areas.Random samples of the sales of the three stores (in $1000)are shown below.

a.Compute the overall mean.
b.State the null and alternative hypotheses to be tested.
c.Show the complete ANOVA table for this test including the test statistic.
d.The null hypothesis is to be tested at 95% confidence.Determine the critical value for this test.What do you conclude?
e.Determine the p-value and use it for the test.

a.Compute the overall mean.
b.State the null and alternative hypotheses to be tested.
c.Show the complete ANOVA table for this test including the test statistic.
d.The null hypothesis is to be tested at 95% confidence.Determine the critical value for this test.What do you conclude?
e.Determine the p-value and use it for the test.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
72
Exhibit 13-7
The following is part of an ANOVA table that was obtained from data regarding three treatments and a total of 15 observations.

Refer to Exhibit 13-7.If at 95% confidence,we want to determine whether or not the means of the populations are equal,the p-value is
A)between 0.01 to 0.025
B)between 0.025 to 0.05
C)between 0.05 to 0.1
D)greater than 0.1
The following is part of an ANOVA table that was obtained from data regarding three treatments and a total of 15 observations.

Refer to Exhibit 13-7.If at 95% confidence,we want to determine whether or not the means of the populations are equal,the p-value is
A)between 0.01 to 0.025
B)between 0.025 to 0.05
C)between 0.05 to 0.1
D)greater than 0.1

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
73
Information regarding the ACT scores of samples of students in three different majors is given below.
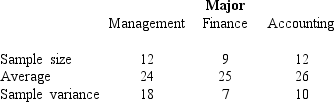
a.Compute the overall sample mean.
b.Set up the ANOVA table for this problem including the test statistic.
c.At 95% confidence,determine the critical value of F.
d.Using the critical value approach,test to determine whether there is a significant difference in the means of the three populations.
e.Determine the p-value and use it for the test.
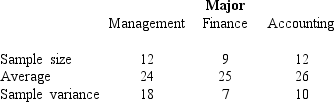
a.Compute the overall sample mean.
b.Set up the ANOVA table for this problem including the test statistic.
c.At 95% confidence,determine the critical value of F.
d.Using the critical value approach,test to determine whether there is a significant difference in the means of the three populations.
e.Determine the p-value and use it for the test.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
74
Exhibit 13-7
The following is part of an ANOVA table that was obtained from data regarding three treatments and a total of 15 observations.

Refer to Exhibit 13-7.The mean square between treatments (MSTR)is
A)36
B)16
C)8
D)32
The following is part of an ANOVA table that was obtained from data regarding three treatments and a total of 15 observations.

Refer to Exhibit 13-7.The mean square between treatments (MSTR)is
A)36
B)16
C)8
D)32

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
75
The heating bills for a selected sample of houses using various forms of heating are given below.(Values are in dollars. )

a.At = 0.05,test to see if there is a significant difference among the average heating bills of the homes.Use the p-value approach.
b.Test the above hypotheses using the critical value approach.Let = .05.

a.At = 0.05,test to see if there is a significant difference among the average heating bills of the homes.Use the p-value approach.
b.Test the above hypotheses using the critical value approach.Let = .05.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
76
In a completely randomized experimental design,7 experimental units were used for the first treatment,9 experimental units for the second treatment,and 14 experimental units for the third treatment.Part of the ANOVA table for this experiment is shown below.

a.Fill in all the blanks in the above ANOVA table.
b.At 95% confidence using both the critical value and p-value approaches,test to see if there is a significant difference among the means.

a.Fill in all the blanks in the above ANOVA table.
b.At 95% confidence using both the critical value and p-value approaches,test to see if there is a significant difference among the means.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
77
Exhibit 13-6
Part of an ANOVA table is shown below.

Refer to Exhibit 13-6.If at 95% confidence we want to determine whether or not the means of the populations are equal,the p-value is
A)greater than 0.1
B)between 0.05 to 0.1
C)between 0.025 to 0.05
D)less than 0.01
Part of an ANOVA table is shown below.

Refer to Exhibit 13-6.If at 95% confidence we want to determine whether or not the means of the populations are equal,the p-value is
A)greater than 0.1
B)between 0.05 to 0.1
C)between 0.025 to 0.05
D)less than 0.01

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
78
Exhibit 13-7
The following is part of an ANOVA table that was obtained from data regarding three treatments and a total of 15 observations.

Refer to Exhibit 13-7.The number of degrees of freedom corresponding to between treatments is
A)12
B)2
C)3
D)4
The following is part of an ANOVA table that was obtained from data regarding three treatments and a total of 15 observations.

Refer to Exhibit 13-7.The number of degrees of freedom corresponding to between treatments is
A)12
B)2
C)3
D)4

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
79
In a completely randomized experimental design,18 experimental units were used for the first treatment,10 experimental units for the second treatment,and 15 experimental units for the third treatment.Part of the ANOVA table for this experiment is shown below.

a.Fill in all the blanks in the above ANOVA table.
b.At 95% confidence,test to see if there is a significant difference among the means.

a.Fill in all the blanks in the above ANOVA table.
b.At 95% confidence,test to see if there is a significant difference among the means.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck
80
Six observations were selected from each of three populations.The data obtained is shown below.

Test at the = 0.05 level to determine if there is a significant difference in the means of the three populations.Use both the critical value and the p-value approaches.

Test at the = 0.05 level to determine if there is a significant difference in the means of the three populations.Use both the critical value and the p-value approaches.

Unlock Deck
Unlock for access to all 113 flashcards in this deck.
Unlock Deck
k this deck


