Deck 4: Introduction to Probability

Question 1

Events are exhaustive if they do not share common outcomes of a sample space.

Answer 1

False

Question 2

Two events A and B are independent if the probability of one does not influence the probability of the other.

Answer 2

True

Question 3

Combinations are used when the order in which different objects are arranged matters.

Answer 3

False

Question 4

Bayes' theorem is used to update prior probabilities based on the arrival of new relevant information.

Question 5

Bayes' theorem uses the total probability rule to update the prior probability of an event that has not been affected by any new evidence.

Question 6

Two events A and B can be both mutually exclusive and independent at the same time.

Question 7

The intersection of two events A and B, denoted by A ∩ B, is the event consisting of all outcomes that are in A and B.

Question 8

Mutually exclusive events may share common outcomes of a sample space.

Question 9

Consider these events.
A = The survey respondent is less than 40 years old.
B = The survey respondent is 40 years or older.
Events A and B are mutually exclusive and exhaustive.

Question 10

Subjective probability is assigned to an event by drawing on logical analysis.

Question 11

The total probability rule is useful only when the unconditional probability is expressed in terms of probabilities conditional on two mutually exclusive and exhaustive events.

Question 12

The probability of a union of events can be greater than 1.

Question 13

The union of two events A and B, denoted by A ∪ B, does not have outcomes from both A and B.

Question 14

Two events can be both mutually exclusive and independent at the same time.

Question 15

The addition rule is used to determine the probability of the union of two events occurring and is defined as a sum of the probabilities of both events.

Question 16

The complement of an event A, denoted by A^c, within the sample space S, is the event consisting of all outcomes of A that are not in S.

Question 17

Permutations are used when the order in which different objects are arranged matters.

Question 18

For an experiment in which a single die is rolled, the sample space may be {1, 1, 2, 3, 4, 5}.

Question 19

Mutually exclusive and collectively exhaustive events contain all outcomes of a sample space, and they do not share any common outcomes.

Question 20

For two independent events A and B, the probability of their intersection is zero.

Question 21

A(n) ________ ________ of an experiment records all possible outcomes of the experiment.

Question 22

The total probability rule is defined as P(A) = P(A ∩B) P(A ∩ B^c)

Question 23

Probabilities can be expressed as fractions, percentages, and ________.

Question 24

Which of the following is not an event when considering the sample space of tossing two coins?

A) {HH, HT}
B) {HH, TT, HT}
C) {HH, TT, HTH}
D) {HH, HT, TH, TT}

Question 25

A sample space contains ________.

A) outcomes of the relevant events.
B) several outcomes of an experiment.
C) all possible outcomes of an experiment.
D) one of several outcomes of an experiment.

Question 26

An intuitive way to express the total probability rule is with the help of a ________.

Question 27

For an experiment in which a single die is rolled, the sample space is ________.

A) {1, 1, 3, 4, 5, 6}.
B) {2, 1, 3, 6, 5, 4}.
C) {1, 2, 3, 4, 4, 5}.
D) All of the above

Question 28

If A and B are ________ ________ events, then the addition rule is defined as
P(A ∪B) = P(A) + P(B).

Question 29

What is probability?

A) Any value between 0 and 1 is always treated as a probability of an event.
B) A numerical value assigned to an event that measures the number of its occurrences.
C) A value between 0 and 1 assigned to an event that measures the likelihood of its occurrence.
D) A value between 0 and 1 assigned to an event that measures the unlikelihood of its occurrence.

Question 30

Events are considered ________ if the occurrence of one is related to the probability of the occurrence of the other.

Question 31

Events are collectively exhaustive if ________.

A) they include all events
B) they are included in all events
C) they contain all outcomes of an experiment
D) they do not share any common outcomes of an experiment

Question 32

The intersection of two events is the event consisting of all outcomes in A ________ B.

Question 33

Bayes' theorem is a rule that uses the total probability rule and the addition rule to update the probability of the event.

Question 34

Which of the following are mutually exclusive events of an experiment in which two coins are tossed?

A) {TT, HH} and {TT}
B) {HT, TH} and {TH}
C) {TT, HT} and (HT}
D) (TT, HH} and {TH}

Question 35

Joint probability of two independent events A and B equals the sum of the individual probabilities of A and B.

Question 36

0! = 0.

Question 37

A(n) ________ probability is calculated as the relative frequency with which an event occurs.

Question 38

In an experiment in which a coin is tossed twice, which of the following represents mutually exclusive and collectively exhaustive events?

A) {TT, HH} and {TT, HT}
B) {HT, TH} and {HH, TH}
C) {TT, HH} and {TH, HT}
D) {TT, HT} and {HT, TH}

Question 39

What is a simple event?

A) An event that contains all outcomes of a sample space
B) An event that contains several outcomes of a sample space
C) An event that contains only one outcome of a sample space
D) All of the above

Question 40

Mutually exclusive events ________.

A) contain all possible outcomes
B) may share common outcomes
C) do not share common outcomes
D) do not contain all possible outcomes

Question 41

Which of the following sets of outcomes described below in I and II represent mutually exclusive events? I. "Your final course grade is an A"; "Your final course grade is a B."
II) "Your final course grade is an A"; "Your final course grade is a Pass."

A) Neither I nor II represent mutually exclusive events.
B) Both I and II represent mutually exclusive events.
C) Only I represents mutually exclusive events.
D) Only II represents mutually exclusive events.

Question 42

The intersection of events A = {apple pie, peach pie, pumpkin pie} and B = {cherry pie, blueberry pie, pumpkin pie} is ________.

A) {pumpkin pie}
B) {apple pie, peach pie, cherry pie, blueberry pie}
C) {apple pie, peach pie, pumpkin pie, cherry pie, blueberry pie}
D) {apple pie, peach pie, pumpkin pie, cherry pie, blueberry pie, pumpkin pie}

Question 43

The intersection of events A and B, denoted by A ∩ B, ________.

A) contains outcomes that are either in A or B
B) contains outcomes that are both in A and B
C) does not contain outcomes that are either in A or B
D) does not contain outcomes that are both in A and B

Question 44

An experiment consists of tossing three fair coins. What is the probability of tossing two tails?

A) 1/8
B) 1/4
C) 3/8
D) 1/2

Question 45

Which of the following sets of outcomes described below in I and II represent mutually exclusive events? I. "You are a freshman"; "You are a senior."
II) "You are a freshman"; "You are an underclassman."

A) Neither I nor II represent mutually exclusive events.
B) Both I and II represent mutually exclusive events.
C) Only I represents mutually exclusive events.
D) Only II represents mutually exclusive events.

Question 46

Mutually exclusive and collectively exhaustive events ________.

A) contain all outcomes in a sample space and may share common outcomes
B) contain all outcomes in a sample space and do not share common outcomes
C) do not have to contain all outcomes in a sample space but do not share common outcomes
D) do not have to contain all outcomes in a sample space and may share common outcomes

Question 47

The odds for encountering rain on a 500-mile car trip are three to one. What is the probability of rain on this trip?

A) 0.25
B) 0.33
C) 0.50
D) 0.75

Question 48

An analyst has a limit order outstanding on a stock. He argues that the probability that the order will execute before the close of trading is 0.20. Thus, the odds for the order executing before the close of trading are

A) one in four.
B) one in five.
C) four to one.
D) five to one.

Question 49

The complement of an event A, within the sample space S, is the event consisting of ________.

A) all outcomes in A that are in S
B) all outcomes in S that are in A
C) all outcomes in S that are not in A
D) all outcomes in A that are not in S

Question 50

An analyst believes the probability that U.S. stock returns exceed long-term corporate bond returns over a five-year period is based on personal assessment. This type of probability is best characterized as a(n) ________.

A) a classical probability
B) empirical probability
C) objective probability
D) subjective probability

Question 51

A probability based on logical analysis rather than on observation or personal judgment is best referred to as a(n) ________.

A) classical probability
B) empirical probability
C) subjective probability
D) None of the above

Question 52

The union of events A and B, denoted by A ∪ B, ________.

A) contains all outcomes that are in A or B
B) contains all outcomes of an experiment
C) contains no outcomes that are in A and B
D) consists only of outcomes that are in A and B

Question 53

After extensive research, an analyst asserts that there is an 80% chance that ABC Corporation will beat its EPS forecast. Analogously, the odds for the company beating its EPS forecast are ________.

A) one in four
B) 1 in 1.25
C) four to one
D) 1.25 to 1

Question 54

For the sample space S = {apple pie, cherry pie, peach pie, pumpkin pie}, what is the complement of A = {pumpkin pie, cherry pie}?

A) {apple pie}
B) {peach pie}
C) {apple pie, peach pie}
D) {pumpkin pie, cherry pie}

Question 55

Let P(A) = 0.6, P(B) = 0.3, and P(A ∪ B^C) = 0.1. Calculate P(A ∩B).

A) 0
B) 0.3
C) 0.9
D) Not enough information to calculate.

Question 56

The odds against winning $1.00 in the lottery are 19 to 1. What is the probability of winning $1.00 in the lottery?

A) 0.05
B) 0.0526
C) 0.90
D) 0.95

Question 57

Which of the following represents a subjective probability?

A) The probability of rolling a 2 on a single die is one in six.
B) Based on a conducted experiment, the probability of tossing a head on an unfair coin is 0.6.
C) A skier believes she has a 10% chance of winning a gold medal.
D) Based on past observation, a manager believes there is a three-in-five chance of retaining an employee for at least one year.

Question 58

The union of events A = {apple pie, peach pie, pumpkin pie} and B = {cherry pie, blueberry pie, pumpkin pie} is ________.

A) {pumpkin pie}
B) {apple pie, peach pie, cherry pie, blueberry pie}
C) {apple pie, peach pie, pumpkin pie, cherry pie, blueberry pie}
D) {apple pie, peach pie, pumpkin pie, cherry pie, blueberry pie, pumpkin pie}

Question 59

Assume the sample space S = {win, loss}. Select the choice that fulfills the requirements of the definition of probability.

A) P({win}) = 0.7, P({loss}) = 0.2
B) P({win}) = 0.7, P({loss}) = −0.3
C) P({win}) = 1.0, P({loss}) = 0.1
D) P({win}) = 0.5, P({loss}) = −0.5

Question 60

Which of the following represents an empirical probability?

A) The probability of tossing a head on a coin is 0.5.
B) The probability of rolling a 2 on a single die is one in six.
C) A skier believes she has a 0.10 chance of winning a gold medal.
D) Based on past observation, a manager believes there is a three-in-five chance of retaining an employee for at least one year.

Question 61

Let A and B be two independent events with P(A) = 0.40 and P(B) = 0.20. Which of the following is correct?

A) P(B|A) = 0.40
B) P(A|B) = 0.08
C) P(A ∩ B) = 0
D) P(A ∪ B) = 0.52

Question 62

Let P(A) = 0.6, P(B) = 0.5, and P((A ∪ B)^c) = 0.1. Calculate P(A | B).

A) 0.20
B) 0.33
C) 0.40
D) Not enough information to calculate.

Question 63

Alison has all her money invested in two mutual funds, A and B. She knows that there is a 40% chance that fund A will rise in price, and a 60% chance that fund B will rise in price given that fund A rises in price. What is the probability that both fund A and fund B will rise in price?

A) 0.24
B) 0.40
C) 0.76
D) 1.00

Question 64

Given an experiment in which a fair coin is tossed three times, the sample space is S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}. Event A is defined as tossing one head (H). What is the event A^c and what is the probability of this event?

A) A^c = {TTT, HHH, HTH}; P(A^c) = 0.375
B) A^c = {TTT, THH, HHH, HHT}; P(A^c) = 0.500
C) A^c = {TTT, HHH, HHT, HTH, HTT}; P(A^c) = 0.625
D) A^c = {TTT, HHT, HTH, THH, HHH}; P(A^c) = 0.625

Question 65

A recent survey shows that the probability of a college student drinking alcohol is 0.6. Further, given that the student is over 21 years old, the probability of drinking alcohol is 0.8. It is also known that 30% of the college students are over 21 years old. The probability of drinking or being over 21 years old is ________.

A) 0.24.
B) 0.42.
C) 0.66.
D) 0.90.

Question 66

Find the missing values marked xx and yy in the following contingency table.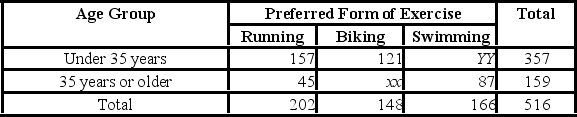

A) xx = 72, yy = 79
B) xx = 27, yy = 77
C) xx = 27, yy = 79
D) xx = 72, yy = 77

Question 67

Two hundred people were asked if they had read a book in the last month. The accompanying contingency table, cross-classified by age, is produced. Given that a respondent read a book in the last month, the probability that he or she is at least 30 years old is the closest to ________.

A) 0.33
B) 0.46
C) 0.65
D) 0.88

Question 68

The following probability table shows probabilities concerning Favorite Subject and Gender. What is the probability of selecting an individual preferring science if she is female?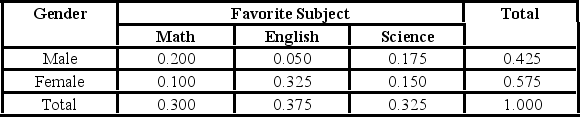

A) 0.2609
B) 0.4615
C) 0.5385
D) 0.7391

Question 69

Alison has all her money invested in two mutual funds, A and B. She knows that there is a 40% chance that fund A will rise in price, and a 60% chance that fund B will rise in price given that fund A rises in price. There is also a 20% chance that fund B will rise in price. What is the probability that at least one of the funds will rise in price?

A) 0.24
B) 0.36
C) 0.60
D) 0.76

Question 70

Two hundred people were asked if they had read a book in the last month. The accompanying contingency table, cross-classified by age, is produced. The probability that a respondent is at least 30 years old is the closest to ________.

A) 0.33
B) 0.46
C) 0.50
D) 0.65

Question 71

The following probability table shows probabilities concerning Favorite Subject and Gender. What is the probability of selecting an individual who is a female or prefers science?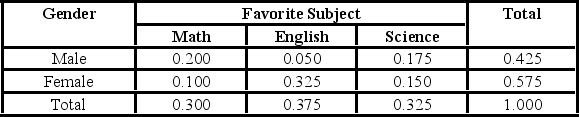

A) 0.250
B) 0.375
C) 0.625
D) 0.750

Question 72

Let P(B|A) = P(B). Suppose A and B are independent. What is the value of P(B|A)?

A) 0.12
B) 0.3
C) 0.4
D) 0.7

Question 73

Peter applied to an accounting firm and a consulting firm. He knows that 30% of similarly qualified applicants receive job offers from the accounting firm, while only 20% of similarly qualified applicants receive job offers from the consulting firm. Assume that receiving an offer from one firm is independent of receiving an offer from the other. What is the probability that both firms offer Peter a job?

A) 0.05
B) 0.06
C) 0.44
D) 0.50

Question 74

The likelihood of Company A's stock price rising is 20%, and the likelihood of Company B's stock price rising is 30%. Assume that the returns of Company A and Company B stock are independent of each other. The probability that the stock price of at least one of the companies will rise is ________.

A) 6%.
B) 10%.
C) 44%.
D) 50%.

Question 75

The contingency table below provides frequencies for the preferred type of exercise for people under the age of 35 and those 35 years of age or older. Find the probability that an individual prefers running.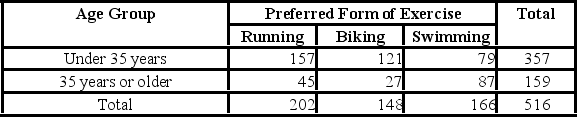

A) 0.3159
B) 0.3915
C) 0.6085
D) 0.6805

Question 76

Two hundred people were asked if they had read a book in the last month. The accompanying contingency table, cross-classified by age, is produced. The probability that a respondent read a book in the last month and is at least 30 years old is the closest to ________.

A) 0.12.
B) 0.33.
C) 0.46.
D) 0.88.

Question 77

The contingency table below provides frequencies for the preferred type of exercise for people under the age of 35 and those 35 years of age or older. Find the probability that an individual prefers running and is under 35 years of age.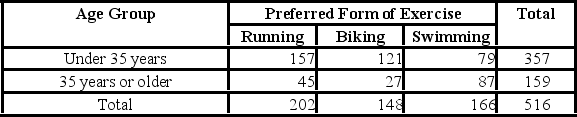

A) 0.3042
B) 0.3915
C) 0.4398
D) 0.6918

Question 78

The contingency table below provides frequencies for the preferred type of exercise for people under the age of 35, and those 35 years of age or older. Find the probability that an individual prefers biking given that he or she is 35 years old or older.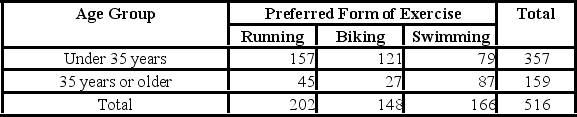

A) 0.1698
B) 0.1824
C) 0.8175
D) 0.8302

Question 79

Alison has all her money invested in two mutual funds, A and B. She knows that there is a 40% chance that fund A will rise in price, and a 60% chance that fund B will rise in price given that fund A rises in price. There is also a 20% chance that fund B will rise in price. What is the probability that neither fund will rise in price?

A) 0.24
B) 0.36
C) 0.40
D) 0.64

Question 80

If A and B are independent events, which of the following is correct?

A) P(A ∪ B) = 0
B) P(A ∩ B) = 0
C) P(A|B) = P(A)
D) P(A ∪ B) = P(A) + P(B)