Deck 13: Analysis of Variance
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/120
Play
Full screen (f)
Deck 13: Analysis of Variance
1
The between-treatments variance is based on a weighted sum of squared differences between the ________.
A) population variances and the overall mean of the data set
B) sample means and the overall mean of the data set
C) sample variances and the overall mean of the data set
D) population means and the overall mean of the data set
A) population variances and the overall mean of the data set
B) sample means and the overall mean of the data set
C) sample variances and the overall mean of the data set
D) population means and the overall mean of the data set
sample means and the overall mean of the data set
2
Which of the following is the correct interpretation of Fisher's 100(1 − α)% confidence interval for μi - μj?
A) If the interval includes zero, the null hypothesis H0: μi - μj = 0, is rejected at a significance level α.
B) If the interval does not include zero, the null hypothesis H0: μi - μj = 0, is rejected at a significance level 100(1− α)%.
C) If the interval does not include zero, the null hypothesis H0: μi - μj = 0, is rejected at a significance level α.
D) If the interval includes zero, the null hypothesis H0: μi - μj = 0, is rejected at a significance level 100(1− α)%.
A) If the interval includes zero, the null hypothesis H0: μi - μj = 0, is rejected at a significance level α.
B) If the interval does not include zero, the null hypothesis H0: μi - μj = 0, is rejected at a significance level 100(1− α)%.
C) If the interval does not include zero, the null hypothesis H0: μi - μj = 0, is rejected at a significance level α.
D) If the interval includes zero, the null hypothesis H0: μi - μj = 0, is rejected at a significance level 100(1− α)%.
If the interval does not include zero, the null hypothesis H0: μi - μj = 0, is rejected at a significance level α.
3
When using Fisher's Least Significant Difference (LSD) where each interval has an error of α, the probability of committing a Type I error for at least one of the individual confidence intervals increases as the number of pairwise comparisons increases.
True
4
Fisher's LSD method is applied when ________.
A) the ANOVA null hypothesis is rejected
B) the ANOVA null hypothesis is not rejected
C) either A or B occur
D) neither A or B occur
A) the ANOVA null hypothesis is rejected
B) the ANOVA null hypothesis is not rejected
C) either A or B occur
D) neither A or B occur

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
5
Which of the following is the Fisher's 100(1− α)% confidence interval for the difference between two population means μi - μj?
A) ( i -
i -  j) ±
j) ± 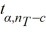
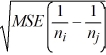
B) ( i -
i -  j) ±
j) ± 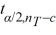
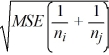
C) ( i -
i -  j) ±
j) ± 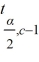
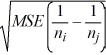
D) ( i -
i -  j) ± tα,c-1
j) ± tα,c-1
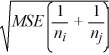
A) (
 i -
i -  j) ±
j) ± 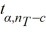
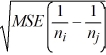
B) (
 i -
i -  j) ±
j) ± 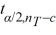
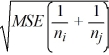
C) (
 i -
i -  j) ±
j) ± 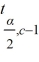
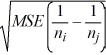
D) (
 i -
i -  j) ± tα,c-1
j) ± tα,c-1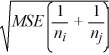

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
6
We use ANOVA to test for differences between population means by examining the amount of variability between the samples relative to the amount of variability within the samples.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
7
When the null hypothesis is rejected in an ANOVA test, Fisher's least significant difference method is superior to Tukey's honestly significant differences method to determine which population means differ.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
8
When two factors interact, the effect of one factor on the mean depends upon the specific value or level for the other factor.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
9
Which of the following is the assumption that is not applicable for a one-way ANOVA test?
A) The populations are normally distributed.
B) The population standard deviations are not all equal.
C) The samples are selected independently.
D) The sample is drawn at random from each population.
A) The populations are normally distributed.
B) The population standard deviations are not all equal.
C) The samples are selected independently.
D) The sample is drawn at random from each population.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
10
One-way ANOVA is used to determine if differences exist between the means of three or more populations under dependent sampling.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
11
The between-treatments variance is the estimate of σ2 based on the variability due to chance.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
12
One-way ANOVA assumes the population standard deviations are unknown and assumed unequal.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
13
If there are five treatments under study, the number of pairwise comparisons is ________.
A) 15
B) 5
C) 20
D) 10
A) 15
B) 5
C) 20
D) 10

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
14
The variability due to chance, also known as the within-treatments variance, is the estimate of σ2 which is not based on the variability ________.
A) between the sample means
B) due to random chance
C) within each sample
D) due to the common population variance
A) between the sample means
B) due to random chance
C) within each sample
D) due to the common population variance

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
15
In general, a blocking variable is used to eliminate the variability in the response due to the levels of the blocking variable.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
16
If the units within each block are randomly assigned to each of the treatments, then the design of the experiment is referred to as a randomized block design.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
17
When using Fisher's LSD method with a given significance level for each interval, the probability of committing a Type I error for at least one comparison increases as the number of ________.
A) pairwise comparisons decreases
B) pairwise comparisons increases
C) sample size increases
D) treatments decreases
A) pairwise comparisons decreases
B) pairwise comparisons increases
C) sample size increases
D) treatments decreases

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
18
Using R, which of the below functions is used to generate an ANOVA table?
A) aov
B) anova
C) Tukey's HSD
D) None of the above
A) aov
B) anova
C) Tukey's HSD
D) None of the above

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
19
The one-way ANOVA null hypothesis is rejected when the ________.
A) two estimates of the variance are relatively close together
B) variability in the sample means can be explained by chance
C) ratio of the within-treatments variance and the between-treatments variance is 1
D) ratio of the within-treatments variance and the between-treatments variance is significantly greater than 1
A) two estimates of the variance are relatively close together
B) variability in the sample means can be explained by chance
C) ratio of the within-treatments variance and the between-treatments variance is 1
D) ratio of the within-treatments variance and the between-treatments variance is significantly greater than 1

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
20
The interaction test is performed before making any conclusions based on the tests for the main effects.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
21
One of the disadvantages of Fisher's LSD method is that the probability of committing at least one ________.
A) Type II error increases as the number of pairwise comparisons increases
B) Type I error increases as the number of pairwise comparisons decreases
C) Type II error increases as the number of pairwise comparisons decreases
D) Type I error increases as the number of pairwise comparisons increases
A) Type II error increases as the number of pairwise comparisons increases
B) Type I error increases as the number of pairwise comparisons decreases
C) Type II error increases as the number of pairwise comparisons decreases
D) Type I error increases as the number of pairwise comparisons increases

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
22
Tukey's Honestly Significant Differences (HSD) method ensures that the probability of at least one Type I error remains fixed irrespective of the number of ________.
A) pairwise comparisons
B) treatments
C) replications within each treatment
D) replications for each combination of factor A and factor B
A) pairwise comparisons
B) treatments
C) replications within each treatment
D) replications for each combination of factor A and factor B

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
23
The following is an incomplete ANOVA table.  The p-value of the test is ________.
The p-value of the test is ________.
A) less than 0.01
B) between 0.01 and 0.025
C) between 0.025 and 0.05
D) greater than 0.05
 The p-value of the test is ________.
The p-value of the test is ________.A) less than 0.01
B) between 0.01 and 0.025
C) between 0.025 and 0.05
D) greater than 0.05

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
24
If the interaction between two factors is not significant, the next tests to be done are ________.
A) none, the analysis is complete
B) none, gather more data
C) tests about the population means of factor A or factor B using two-way ANOVA without interaction
D) Tukey's confidence intervals
A) none, the analysis is complete
B) none, gather more data
C) tests about the population means of factor A or factor B using two-way ANOVA without interaction
D) Tukey's confidence intervals

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
25
The following is an incomplete ANOVA table.  The sum of squares due to treatments is ________.
The sum of squares due to treatments is ________.
A) 10
B) 25
C) 75
D) 100
 The sum of squares due to treatments is ________.
The sum of squares due to treatments is ________.A) 10
B) 25
C) 75
D) 100

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
26
In a two-way ANOVA test, how many null hypotheses are tested?
A) 1
B) 1 or 2
C) 2 or 3
D) More than 3
A) 1
B) 1 or 2
C) 2 or 3
D) More than 3

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
27
The following is an incomplete ANOVA table.  The mean square error is ________.
The mean square error is ________.
A) 1.333
B) 9.375
C) 25
D) 75
 The mean square error is ________.
The mean square error is ________.A) 1.333
B) 9.375
C) 25
D) 75

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
28
A researcher with the Ministry of Transportation is commissioned to study the drive times to work (one-way) for U.S. cities. The underlying hypothesis is that average commute times are different across cities. To test the hypothesis, the researcher randomly selects six people from each of the four cities and records their one-way commute times to work. Refer to the below data on one-way commute times (in minutes) to work. Note that the grand mean is 36.625. 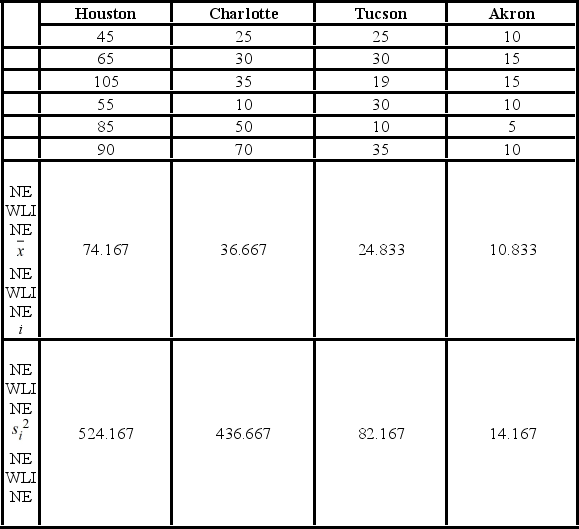 Which of the following is the sum of squares due to treatments?
Which of the following is the sum of squares due to treatments?
A) 5,285.83
B) 13,281.79
C) 18,567.63
D) 4,427.26
 Which of the following is the sum of squares due to treatments?
Which of the following is the sum of squares due to treatments?A) 5,285.83
B) 13,281.79
C) 18,567.63
D) 4,427.26

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
29
The following is an incomplete ANOVA table.  For the within groups category, the degrees of freedom are ________.
For the within groups category, the degrees of freedom are ________.
A) 6
B) 7
C) 8
D) 9
 For the within groups category, the degrees of freedom are ________.
For the within groups category, the degrees of freedom are ________.A) 6
B) 7
C) 8
D) 9

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
30
Tukey's 100(1 − α)% confidence interval for the difference between two population means μi - μj for balanced data is given by ________.
A) ( i -
i -  j) ±
j) ± 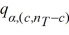
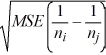
B) ( i -
i -  j) ±
j) ± 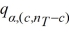
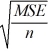
C) ( i -
i -  j) ±
j) ± 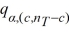
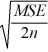
D) ( i -
i -  j) ±
j) ± 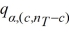
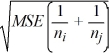
A) (
 i -
i -  j) ±
j) ± 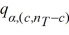
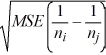
B) (
 i -
i -  j) ±
j) ± 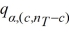
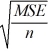
C) (
 i -
i -  j) ±
j) ± 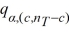
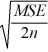
D) (
 i -
i -  j) ±
j) ± 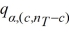
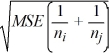

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
31
A researcher with the Ministry of Transportation is commissioned to study the drive times to work (one-way) for U.S. cities. The underlying hypothesis is that average commute times are different across cities. To test the hypothesis, the researcher randomly selects six people from each of the four cities and records their one-way commute times to work. Refer to the below data on one-way commute times (in minutes) to work. Note that the grand mean is 36.625. 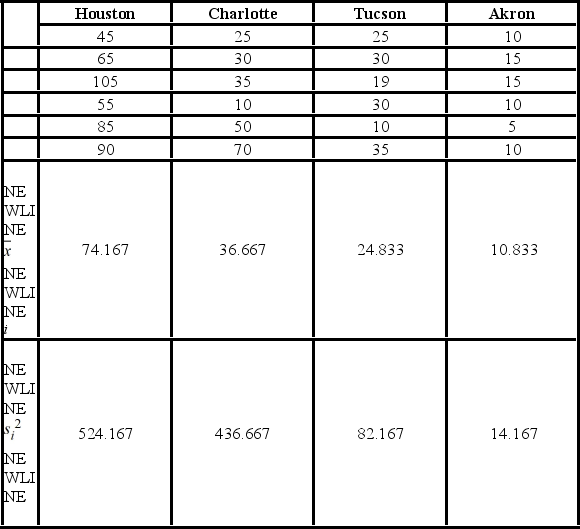
The competing hypotheses about the mean commute times are ________.
A) H0: ?1 = ?2 = ?3, HA: Not all population means are equal
B) H0: Not all population means are equal, HA: ?1 = ?2 = ?3
C) H0: ?1 = ?2 = ?3 = ?4, HA: Not all population means are equal
D) H0: Not all population means are equal, HA: ?1 = ?2 = ?3 = ?4

The competing hypotheses about the mean commute times are ________.
A) H0: ?1 = ?2 = ?3, HA: Not all population means are equal
B) H0: Not all population means are equal, HA: ?1 = ?2 = ?3
C) H0: ?1 = ?2 = ?3 = ?4, HA: Not all population means are equal
D) H0: Not all population means are equal, HA: ?1 = ?2 = ?3 = ?4

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
32
Which of the below is not true about Tukey's 100(1−α)% confidence interval for the difference between two population means?
A) Tukey's intervals are narrower than those based on Fisher's method.
B) Tukey's intervals are narrower than those based on the two-sample T method.
C) Tukey's intervals use a reduced significance level in comparison to Fisher's method
D) Tukey's intervals use an increased significance level in comparison to Fisher's method
A) Tukey's intervals are narrower than those based on Fisher's method.
B) Tukey's intervals are narrower than those based on the two-sample T method.
C) Tukey's intervals use a reduced significance level in comparison to Fisher's method
D) Tukey's intervals use an increased significance level in comparison to Fisher's method

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
33
A researcher with the Ministry of Transportation is commissioned to study the drive times to work (one-way) for U.S. cities. The underlying hypothesis is that average commute times are different across cities. To test the hypothesis, the researcher randomly selects six people from each of the four cities and records their one-way commute times to work. Refer to the below data on one-way commute times (in minutes) to work. Note that the grand mean is 36.625. 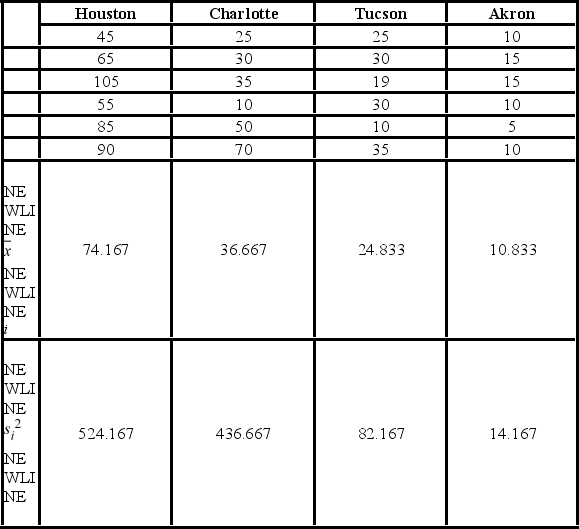 Which of the following is the sum of squared errors?
Which of the following is the sum of squared errors?
A) 264.29
B) 5,285.83
C) 18,567.63
D) 13,281.79
 Which of the following is the sum of squared errors?
Which of the following is the sum of squared errors?A) 264.29
B) 5,285.83
C) 18,567.63
D) 13,281.79

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
34
The following is an incomplete ANOVA table.  The value of the test statistic is ________.
The value of the test statistic is ________.
A) 1.333
B) 9.375
C) 12.5
D) 100
 The value of the test statistic is ________.
The value of the test statistic is ________.A) 1.333
B) 9.375
C) 12.5
D) 100

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
35
Tukey's HSD method uses ________ instead of ________ when compared to Fisher's LSD method for pairwise comparisons.
A) t values; studentized range values
B) studentized range values; F values
C) F values; t values
D) studentized range values; t values
A) t values; studentized range values
B) studentized range values; F values
C) F values; t values
D) studentized range values; t values

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
36
A researcher with the Ministry of Transportation is commissioned to study the drive times to work (one-way) for U.S. cities. The underlying hypothesis is that average commute times are different across cities. To test the hypothesis, the researcher randomly selects six people from each of the four cities and records their one-way commute times to work. Refer to the below data on one-way commute times (in minutes) to work. Note that the grand mean is 36.625. 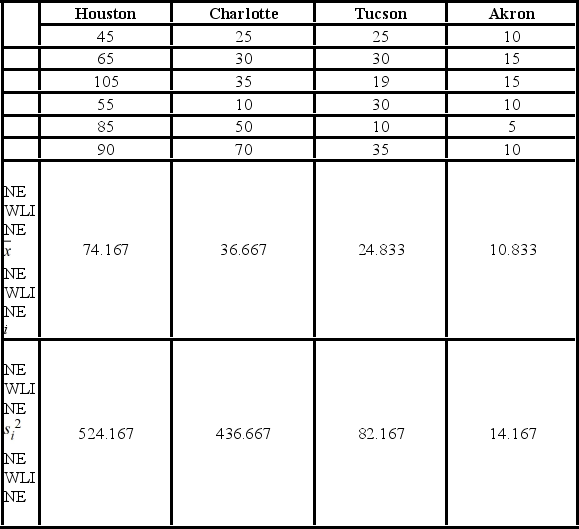 The value of the test statistic is ________.
The value of the test statistic is ________.
A) 0.06
B) 0.40
C) 2.51
D) 16.75
 The value of the test statistic is ________.
The value of the test statistic is ________.A) 0.06
B) 0.40
C) 2.51
D) 16.75

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
37
The following is an incomplete ANOVA table.  At the 5% significance level, the critical value is ________.
At the 5% significance level, the critical value is ________.
A) 3.11
B) 4.46
C) 6.06
D) 8.65
 At the 5% significance level, the critical value is ________.
At the 5% significance level, the critical value is ________.A) 3.11
B) 4.46
C) 6.06
D) 8.65

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
38
A researcher with the Ministry of Transportation is commissioned to study the drive times to work (one-way) for U.S. cities. The underlying hypothesis is that average commute times are different across cities. To test the hypothesis, the researcher randomly selects six people from each of the four cities and records their one-way commute times to work. Refer to the below data on one-way commute times (in minutes) to work. Note that the grand mean is 36.625. 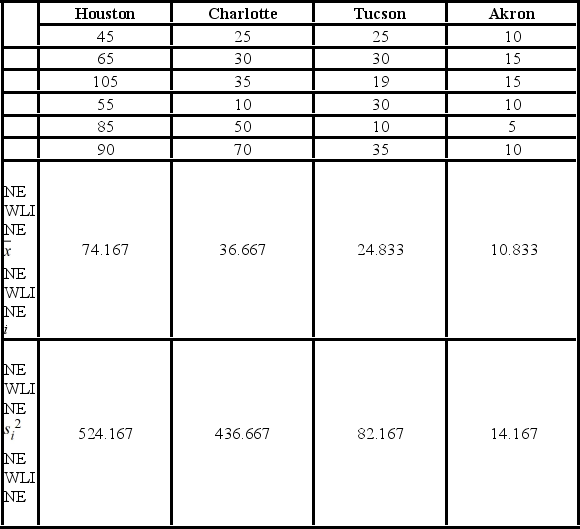 Which of the following is the mean square for treatments?
Which of the following is the mean square for treatments?
A) 18,567.63
B) 13,281.79
C) 5,285.83
D) 4,427.26
 Which of the following is the mean square for treatments?
Which of the following is the mean square for treatments?A) 18,567.63
B) 13,281.79
C) 5,285.83
D) 4,427.26

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
39
A researcher with the Ministry of Transportation is commissioned to study the drive times to work (one-way) for U.S. cities. The underlying hypothesis is that average commute times are different across cities. To test the hypothesis, the researcher randomly selects six people from each of the four cities and records their one-way commute times to work. Refer to the below data on one-way commute times (in minutes) to work. Note that the grand mean is 36.625. 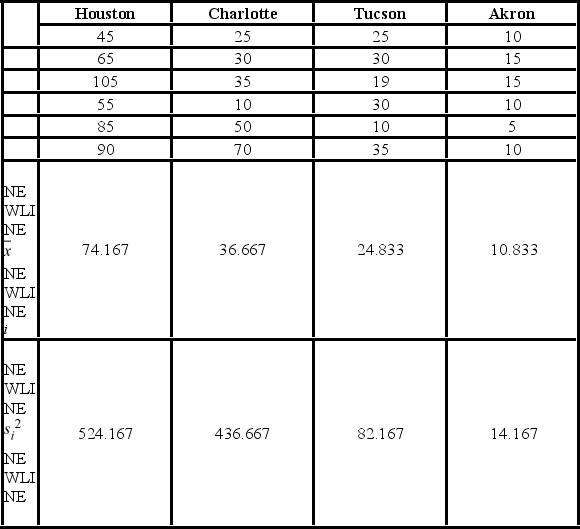 At the 5% significance level, the critical value is ________.
At the 5% significance level, the critical value is ________.
A) 2.38
B) 3.10
C) 3.86
D) 4.94
 At the 5% significance level, the critical value is ________.
At the 5% significance level, the critical value is ________.A) 2.38
B) 3.10
C) 3.86
D) 4.94

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
40
Which of these null hypotheses is applicable for a two-way ANOVA test with interaction?
A) There is interaction between factors A and B.
B) Factor A and factor B means differ.
C) There is no interaction between factors A and B.
D) Factor A and factor B means do not differ.
A) There is interaction between factors A and B.
B) Factor A and factor B means differ.
C) There is no interaction between factors A and B.
D) Factor A and factor B means do not differ.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
41
A researcher with the Ministry of Transportation is commissioned to study the drive times to work (one-way) for U.S. cities. The underlying hypothesis is that average commute times are different across cities. To test the hypothesis, the researcher randomly selects six people from each of the four cities and records their one-way commute times to work. Refer to the below data on one-way commute times (in minutes) to work. Note that the grand mean is 36.625. 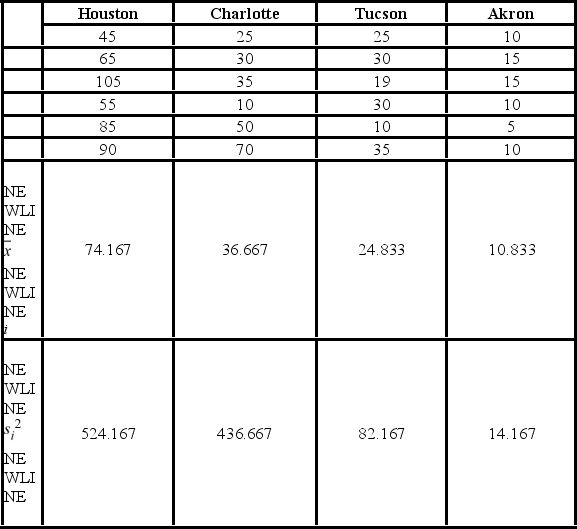 Based on the sample standard deviation, the one-way ANOVA assumption that is likely not met is ________.
Based on the sample standard deviation, the one-way ANOVA assumption that is likely not met is ________.
A) the populations are normally distributed.
B) the population standard deviations are assumed to be equal.
C) the samples are independent.
D) None of these choices is correct.
 Based on the sample standard deviation, the one-way ANOVA assumption that is likely not met is ________.
Based on the sample standard deviation, the one-way ANOVA assumption that is likely not met is ________.A) the populations are normally distributed.
B) the population standard deviations are assumed to be equal.
C) the samples are independent.
D) None of these choices is correct.

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
42
A police chief wants to determine if crime rates are different for four different areas of the city (East(1), West(2), North(3), and South(4) sides), and obtains data on the number of crimes per day in each area. The one-way ANOVA table is shown below.  The p-value for the test is ________.
The p-value for the test is ________.
A) less than 0.01
B) between 0.01 and 0.025
C) between 0.025 and 0.05
D) greater than 0.05
 The p-value for the test is ________.
The p-value for the test is ________.A) less than 0.01
B) between 0.01 and 0.025
C) between 0.025 and 0.05
D) greater than 0.05

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
43
A police chief wants to determine if crime rates are different for four different areas of the city (East(1), West(2), North(3), and South(4) sides), and obtains data on the number of crimes per day in each area. The Tukey's confidence intervals are shown below. 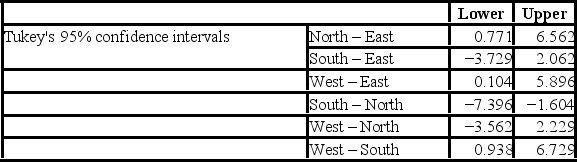 At the 1% significance level, the conclusion from Tukey's confidence intervals is we ________.
At the 1% significance level, the conclusion from Tukey's confidence intervals is we ________.
A) cannot conclude the mean number of crimes differs for West and East
B) cannot conclude the mean number of crimes differs for West and South
C) cannot conclude the mean number of crimes differs for South and North
D) cannot conclude the mean number of crimes differs for West and North
 At the 1% significance level, the conclusion from Tukey's confidence intervals is we ________.
At the 1% significance level, the conclusion from Tukey's confidence intervals is we ________.A) cannot conclude the mean number of crimes differs for West and East
B) cannot conclude the mean number of crimes differs for West and South
C) cannot conclude the mean number of crimes differs for South and North
D) cannot conclude the mean number of crimes differs for West and North

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
44
A police chief wants to determine if crime rates are different for four different areas of the city (East(1), West(2), North(3), and South(4) sides), and obtains data on the number of crimes per day in each area. The one-way ANOVA table is shown below.  At the 1% significance level, the conclusion for the hypothesis test is ________.
At the 1% significance level, the conclusion for the hypothesis test is ________.
A) reject the null hypothesis; we can conclude that not all mean number of crimes are equal
B) do not reject the null hypothesis; we can conclude not all mean number of crimes are equal
C) reject the null hypothesis; we cannot conclude that not all mean number of crimes are equal
D) do not reject the null hypothesis; we cannot conclude that not all mean number of crimes are equal
 At the 1% significance level, the conclusion for the hypothesis test is ________.
At the 1% significance level, the conclusion for the hypothesis test is ________.A) reject the null hypothesis; we can conclude that not all mean number of crimes are equal
B) do not reject the null hypothesis; we can conclude not all mean number of crimes are equal
C) reject the null hypothesis; we cannot conclude that not all mean number of crimes are equal
D) do not reject the null hypothesis; we cannot conclude that not all mean number of crimes are equal

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
45
A researcher wants to understand how an annual mortgage payment (in dollars) depends on income level and zonal location using a two-way ANOVA without interaction. The data and an incomplete ANOVA table are shown below. 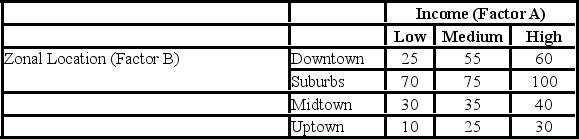
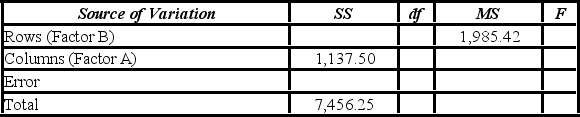 Which of the following is the value of the test statistic for factor A?
Which of the following is the value of the test statistic for factor A?
A) 4.76
B) 5.14
C) 9.41
D) 32.86

 Which of the following is the value of the test statistic for factor A?
Which of the following is the value of the test statistic for factor A?A) 4.76
B) 5.14
C) 9.41
D) 32.86

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
46
The ANOVA test performed for determined that not all mean commute times across the four cities are equal. However, it did not indicate which means differed. To find out which population means differ requires further analysis of the direction and the statistical significance of the difference between paired population means. Tukey 95% confidence intervals are shown below. 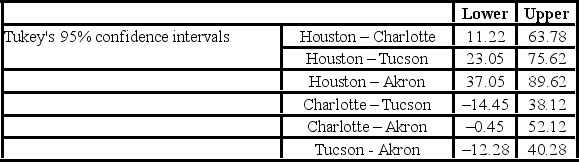 Which of these pairs of cities show a significant difference between the average commute times to work?
Which of these pairs of cities show a significant difference between the average commute times to work?
A) Charlotte - Tucson
B) Charlotte - Akron
C) Houston - Charlotte
D) Tucson- Akron
 Which of these pairs of cities show a significant difference between the average commute times to work?
Which of these pairs of cities show a significant difference between the average commute times to work?A) Charlotte - Tucson
B) Charlotte - Akron
C) Houston - Charlotte
D) Tucson- Akron

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
47
The ANOVA test performed for determined that not all mean commute times across the four cities are equal. However, it did not indicate which means differed. To find out which population means differ requires further analysis of the direction and the statistical significance of the difference between paired population means. Fisher's 95% confidence intervals are shown below. 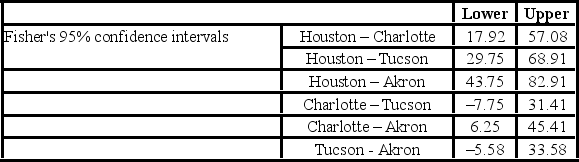 Which of these pair of cities show no significant difference between the average commute times to work?
Which of these pair of cities show no significant difference between the average commute times to work?
A) Houston, Akron
B) Charlotte, Akron
C) Charlotte, Tucson
D) Houston, Tucson
 Which of these pair of cities show no significant difference between the average commute times to work?
Which of these pair of cities show no significant difference between the average commute times to work?A) Houston, Akron
B) Charlotte, Akron
C) Charlotte, Tucson
D) Houston, Tucson

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
48
The ANOVA test performed for determined that not all mean commute times across the four cities are equal. However, it did not indicate which means differed. To find out which population means differ requires further analysis of the direction and the statistical significance of the difference between paired population means. Tukey 95% confidence intervals are shown below. 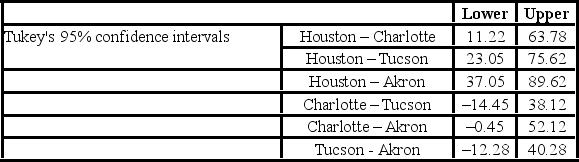 Which of the following is the studentized range value with α = 0.05 for Tukey's HSD method?
Which of the following is the studentized range value with α = 0.05 for Tukey's HSD method?
A) 5.02
B) 3.58
C) 3.96
D) 4.64
 Which of the following is the studentized range value with α = 0.05 for Tukey's HSD method?
Which of the following is the studentized range value with α = 0.05 for Tukey's HSD method?A) 5.02
B) 3.58
C) 3.96
D) 4.64

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
49
A police chief wants to determine if crime rates are different for four different areas of the city (East(1), West(2), North(3), and South(4) sides), and obtains data on the number of crimes per day in each area. The one-way ANOVA table is shown below.  The competing hypotheses about the mean crime rates are ________.
The competing hypotheses about the mean crime rates are ________.
A) H0: μ1 = μ2 = μ3, HA: Not all population means are equal
B) H0: Not all population means are equal, HA: μ1 = μ2 = μ3
C) H0: μ1 = μ2 = μ3 = μ4, HA: Not all population means are equal
D) H0: Not all population means are equal, HA: μ1 = μ2 = μ3 = μ4
 The competing hypotheses about the mean crime rates are ________.
The competing hypotheses about the mean crime rates are ________.A) H0: μ1 = μ2 = μ3, HA: Not all population means are equal
B) H0: Not all population means are equal, HA: μ1 = μ2 = μ3
C) H0: μ1 = μ2 = μ3 = μ4, HA: Not all population means are equal
D) H0: Not all population means are equal, HA: μ1 = μ2 = μ3 = μ4

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
50
A researcher with the Ministry of Transportation is commissioned to study the drive times to work (one-way) for U.S. cities. The underlying hypothesis is that average commute times are different across cities. To test the hypothesis, the researcher randomly selects six people from each of the four cities and records their one-way commute times to work. Refer to the below data on one-way commute times (in minutes) to work. Note that the grand mean is 36.625. 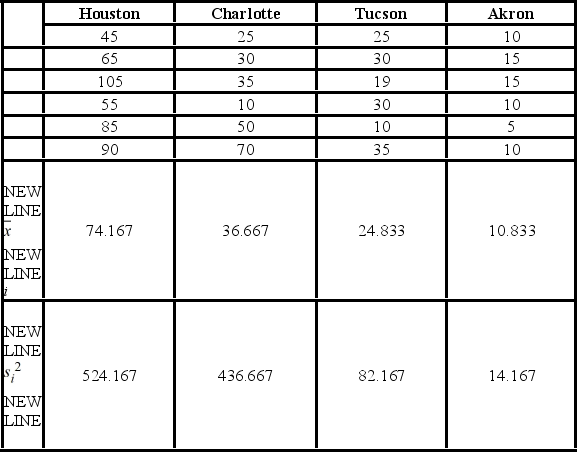 The p-value for the test is ________.
The p-value for the test is ________.
A) less than 0.01
B) between 0.01 and 0.025
C) between 0.025 and 0.05
D) greater than 0.05
 The p-value for the test is ________.
The p-value for the test is ________.A) less than 0.01
B) between 0.01 and 0.025
C) between 0.025 and 0.05
D) greater than 0.05

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
51
The ANOVA test performed for determined that not all mean commute times across the four cities are equal. However, it did not indicate which means differed. To find out which population means differ requires further analysis of the direction and the statistical significance of the difference between paired population means. Fisher 95% confidence intervals are shown below. 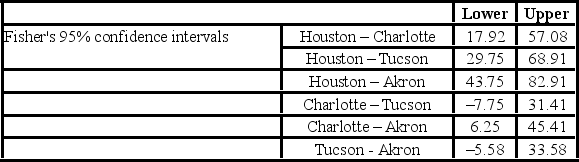 Which of the following is the
Which of the following is the 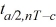 value used to calculate the Fisher's 95% confidence intervals?
value used to calculate the Fisher's 95% confidence intervals?
A) 1.725
B) 2.086
C) 2.080
D) 2.090
 Which of the following is the
Which of the following is the 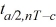 value used to calculate the Fisher's 95% confidence intervals?
value used to calculate the Fisher's 95% confidence intervals?A) 1.725
B) 2.086
C) 2.080
D) 2.090

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
52
A researcher wants to understand how an annual mortgage payment (in dollars) depends on income level and zonal location using a two-way ANOVA without interaction. The data and an incomplete ANOVA table are shown below. 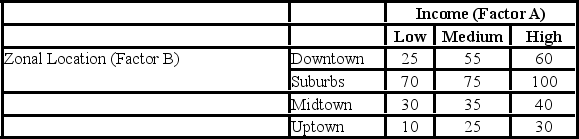
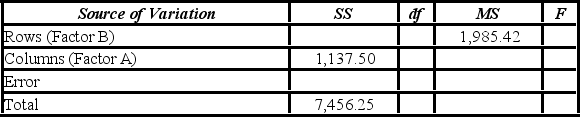 How many degrees of freedom are there for factors A and B?
How many degrees of freedom are there for factors A and B?
A) 2, 3
B) 3, 4
C) 3, 6
D) 2, 4

 How many degrees of freedom are there for factors A and B?
How many degrees of freedom are there for factors A and B?A) 2, 3
B) 3, 4
C) 3, 6
D) 2, 4

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
53
The ANOVA test performed for determined that not all mean commute times across the four cities are equal. However, it did not indicate which means differed. To find out which population means differ requires further analysis of the direction and the statistical significance of the difference between paired population means. Tukey's 95% confidence intervals are shown below. 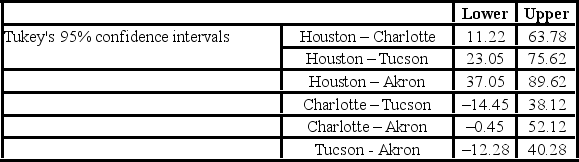 How many pairs of cities show a significant difference between the average commute times to work?
How many pairs of cities show a significant difference between the average commute times to work?
A) 2
B) 3
C) 4
D) 6
 How many pairs of cities show a significant difference between the average commute times to work?
How many pairs of cities show a significant difference between the average commute times to work?A) 2
B) 3
C) 4
D) 6

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
54
A researcher wants to understand how an annual mortgage payment (in dollars) depends on income level and zonal location using a two-way ANOVA without interaction. The data and an incomplete ANOVA table are shown below. 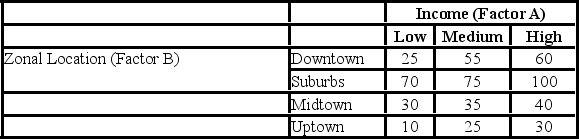
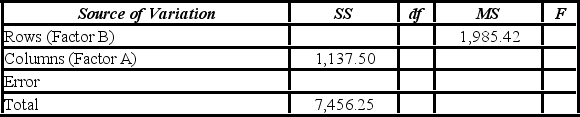 Which of the following is the value of the test statistic for factor B?
Which of the following is the value of the test statistic for factor B?
A) 4.76
B) 5.14
C) 9.41
D) 32.86

 Which of the following is the value of the test statistic for factor B?
Which of the following is the value of the test statistic for factor B?A) 4.76
B) 5.14
C) 9.41
D) 32.86

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
55
A police chief wants to determine if crime rates are different for four different areas of the city (East(1), West(2), North(3), and South(4) sides), and obtains data on the number of crimes per day in each area. The one-way ANOVA table is shown below.  At the 1% significance level, the critical value is ________.
At the 1% significance level, the critical value is ________.
A) 2.38
B) 3.10
C) 3.86
D) 4.94
 At the 1% significance level, the critical value is ________.
At the 1% significance level, the critical value is ________.A) 2.38
B) 3.10
C) 3.86
D) 4.94

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
56
The ANOVA test performed for determined that not all mean commute times across the four cities are equal. However, it did not indicate which means differed. To find out which population means differ requires further analysis of the direction and the statistical significance of the difference between paired population means. Fisher 95% confidence intervals are shown below. 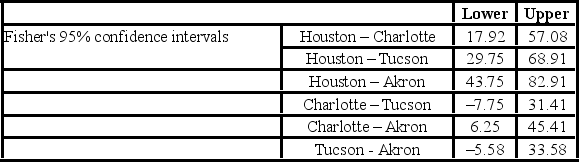 How many pairs of cities show a significant difference in average commute times to work?
How many pairs of cities show a significant difference in average commute times to work?
A) 2
B) 3
C) 4
D) 6
 How many pairs of cities show a significant difference in average commute times to work?
How many pairs of cities show a significant difference in average commute times to work?A) 2
B) 3
C) 4
D) 6

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
57
A researcher with the Ministry of Transportation is commissioned to study the drive times to work (one-way) for U.S. cities. The underlying hypothesis is that average commute times are different across cities. To test the hypothesis, the researcher randomly selects six people from each of the four cities and records their one-way commute times to work. Refer to the below data on one-way commute times (in minutes) to work. Note that the grand mean is 36.625. 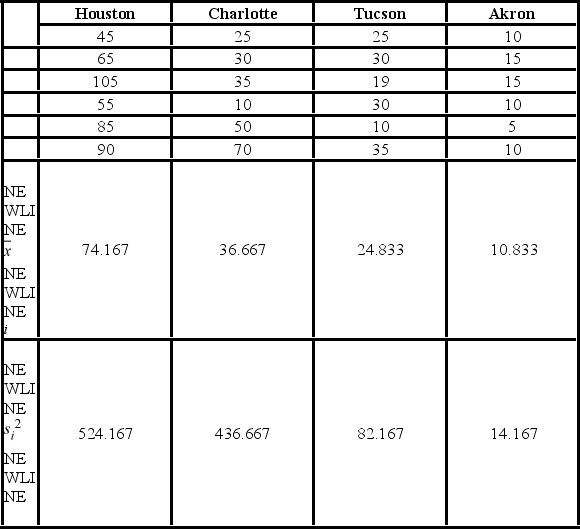 The conclusion for the hypothesis test is ________.
The conclusion for the hypothesis test is ________.
A) to reject the null hypothesis; we cannot conclude that not all mean commute times are equal
B) do not reject the null hypothesis; we cannot conclude that not all mean commute times are equal
C) reject the null hypothesis; we can conclude that not all mean commute times are equal
D) do not reject the null hypothesis; we can conclude that not all mean commute times are equal
 The conclusion for the hypothesis test is ________.
The conclusion for the hypothesis test is ________.A) to reject the null hypothesis; we cannot conclude that not all mean commute times are equal
B) do not reject the null hypothesis; we cannot conclude that not all mean commute times are equal
C) reject the null hypothesis; we can conclude that not all mean commute times are equal
D) do not reject the null hypothesis; we can conclude that not all mean commute times are equal

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
58
A police chief wants to determine if crime rates are different for four different areas of the city (East(1), West(2), North(3), and South sides), and obtains data on the number of crimes per day in each area. The one-way ANOVA table is shown below.  The degrees of freedom for the hypothesis test are ________.
The degrees of freedom for the hypothesis test are ________.
A) 4, 20
B) 3, 23
C) 3, 20
D) 4, 23
 The degrees of freedom for the hypothesis test are ________.
The degrees of freedom for the hypothesis test are ________.A) 4, 20
B) 3, 23
C) 3, 20
D) 4, 23

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
59
The ANOVA test performed for determined that not all mean commute times across the four cities are equal. However, it did not indicate which means differed. To find out which population means differ requires further analysis of the direction and the statistical significance of the difference between paired population means. Tukey's 95% confidence intervals are shown below. 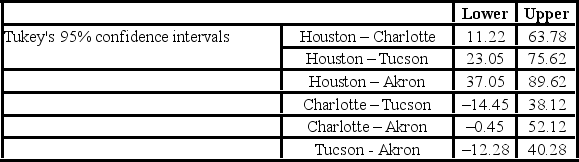 The conclusion of the Tukey confidence intervals is ________.
The conclusion of the Tukey confidence intervals is ________.
A) the mean commute time in Houston is different from the mean commute time in Charlotte, Tucson, and Akron
B) the mean commute time in Charlotte is different from the mean commute time in Houston, Tucson, and Akron
C) the mean commute time in Tucson is different from the mean commute time in Houston, Charlotte, and Akron
D) the mean commute time in Akron is different from the mean time in Houston, Charlotte, and Tucson
 The conclusion of the Tukey confidence intervals is ________.
The conclusion of the Tukey confidence intervals is ________.A) the mean commute time in Houston is different from the mean commute time in Charlotte, Tucson, and Akron
B) the mean commute time in Charlotte is different from the mean commute time in Houston, Tucson, and Akron
C) the mean commute time in Tucson is different from the mean commute time in Houston, Charlotte, and Akron
D) the mean commute time in Akron is different from the mean time in Houston, Charlotte, and Tucson

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
60
A researcher wants to understand how an annual mortgage payment (in dollars) depends on income level and zonal location using a two-way ANOVA without interaction. The data and an incomplete ANOVA table are shown below. 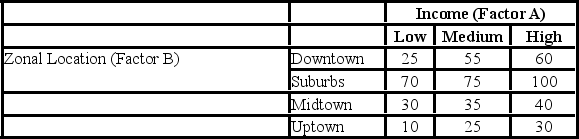
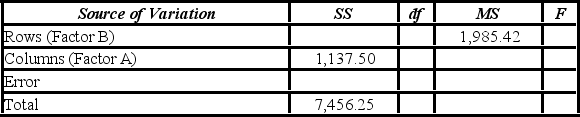 Which of the following are the total degrees of freedom?
Which of the following are the total degrees of freedom?
A) 10
B) 11
C) 12
D) 6

 Which of the following are the total degrees of freedom?
Which of the following are the total degrees of freedom?A) 10
B) 11
C) 12
D) 6

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
61
A market researcher is studying the spending habits of people across age groups. The amount of money spent by each individual is classified by spending category (Dining out, Shopping, or Electronics) - Factor A, and generation (Gen-X, Gen-Y, Gen-Z, or Baby Boomers) - Factor B. An incomplete ANOVA table is shown below 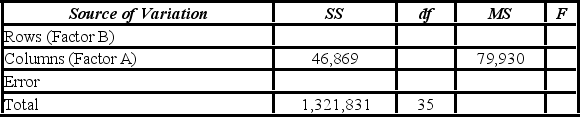 The p-value for the hypothesis test about factor B is ________.
The p-value for the hypothesis test about factor B is ________.
A) less than 0.01
B) between 0.01 and 0.025
C) between 0.025 and 0.05
D) greater than 0.05
 The p-value for the hypothesis test about factor B is ________.
The p-value for the hypothesis test about factor B is ________.A) less than 0.01
B) between 0.01 and 0.025
C) between 0.025 and 0.05
D) greater than 0.05

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
62
A researcher wants to understand how an annual mortgage payment (in dollars) depends on income level and zonal location using a two-way ANOVA without interaction. The data and an incomplete ANOVA table are shown below. 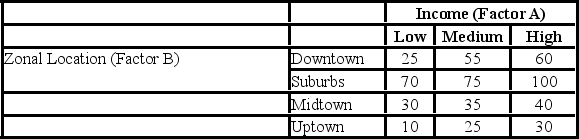
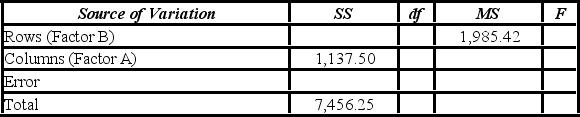 At the 1% significance level, the critical value for the hypothesis test about factor B is ________.
At the 1% significance level, the critical value for the hypothesis test about factor B is ________.
A) 3.29
B) 4.76
C) 6.60
D) 9.78

 At the 1% significance level, the critical value for the hypothesis test about factor B is ________.
At the 1% significance level, the critical value for the hypothesis test about factor B is ________.A) 3.29
B) 4.76
C) 6.60
D) 9.78

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
63
A researcher wants to understand how an annual mortgage payment (in dollars) depends on income level and zonal location using a two-way ANOVA without interaction. The data and an incomplete ANOVA table are shown below. 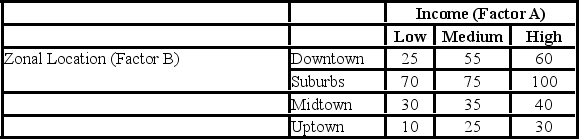
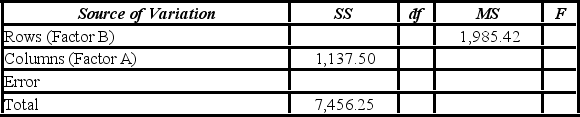 The p-value for the hypothesis test about factor B is ________.
The p-value for the hypothesis test about factor B is ________.
A) less than 0.01
B) between 0.01 and 0.025
C) between 0.025 and 0.05
D) greater than 0.05

 The p-value for the hypothesis test about factor B is ________.
The p-value for the hypothesis test about factor B is ________.A) less than 0.01
B) between 0.01 and 0.025
C) between 0.025 and 0.05
D) greater than 0.05

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
64
A market researcher is studying the spending habits of people across age groups. The amount of money spent by each individual is classified by spending category (Dining out, Shopping, or Electronics) - Factor A, and generation (Gen-X, Gen-Y, Gen-Z, or Baby Boomers) - Factor B. An incomplete ANOVA table is shown below.  Which of the following is the value of MSB?
Which of the following is the value of MSB?
A) 15,623
B) 79,930
C) 37,170
D) 1,321,831
 Which of the following is the value of MSB?
Which of the following is the value of MSB?A) 15,623
B) 79,930
C) 37,170
D) 1,321,831

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
65
A market researcher is studying the spending habits of people across age groups. The amount of money spent by each individual is classified by spending category (Dining out, Shopping, or Electronics) - Factor A, and generation (Gen-X, Gen-Y, Gen-Z, or Baby Boomers) - Factor B. An incomplete ANOVA table is shown below.  For factor A, the value of the test statistic is ________.
For factor A, the value of the test statistic is ________.
A) 3.21
B) 2.15
C) 16.43
D) 3
 For factor A, the value of the test statistic is ________.
For factor A, the value of the test statistic is ________.A) 3.21
B) 2.15
C) 16.43
D) 3

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
66
A researcher wants to understand how an annual mortgage payment (in dollars) depends on income level and zonal location using a two-way ANOVA without interaction. The data and an incomplete ANOVA table are shown below. 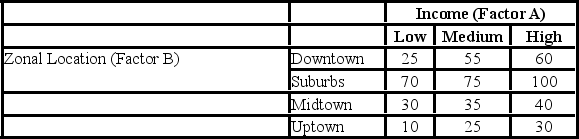
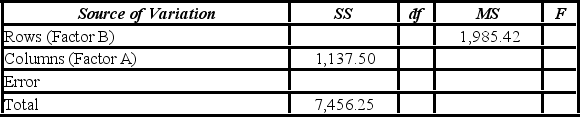 The p-value for the hypothesis test about factor A is ________.
The p-value for the hypothesis test about factor A is ________.
A) less than 0.01
B) between 0.01 and 0.025
C) between 0.025 and 0.05
D) greater than 0.05

 The p-value for the hypothesis test about factor A is ________.
The p-value for the hypothesis test about factor A is ________.A) less than 0.01
B) between 0.01 and 0.025
C) between 0.025 and 0.05
D) greater than 0.05

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
67
A market researcher is studying the spending habits of people across age groups. The amount of money spent by each individual is classified by spending category (Dining out, Shopping, or Electronics) and generation (Gen-X, Gen-Y, Gen-Z, or Baby Boomers). The data and an incomplete ANOVA table are shown below. 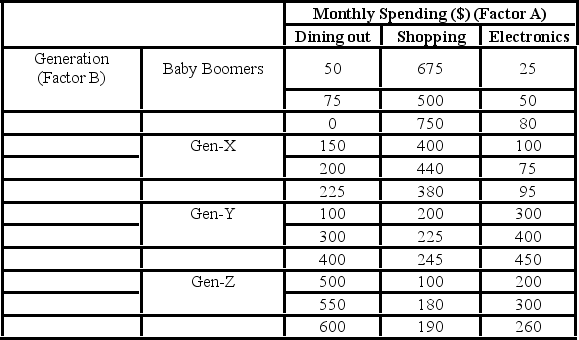
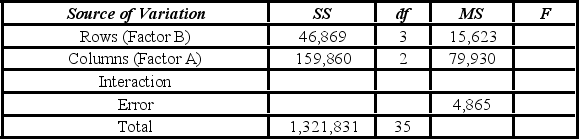 For the analysis with an interaction between spending category and generation, the first hypothesis test to conduct should be about ________.
For the analysis with an interaction between spending category and generation, the first hypothesis test to conduct should be about ________.
A) the average spending across spending
B) the interaction between spending and generation
C) the average spending across generation
D) both the average spending across spending and generation

 For the analysis with an interaction between spending category and generation, the first hypothesis test to conduct should be about ________.
For the analysis with an interaction between spending category and generation, the first hypothesis test to conduct should be about ________.A) the average spending across spending
B) the interaction between spending and generation
C) the average spending across generation
D) both the average spending across spending and generation

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
68
A market researcher is studying the spending habits of people across age groups. The amount of money spent by each individual is classified by spending category (Dining out, Shopping, or Electronics) - Factor A, and generation (Gen-X, Gen-Y, Gen-Z, or Baby Boomers) - Factor B. An incomplete ANOVA table is shown below.  Which of the following is the value of SSA?
Which of the following is the value of SSA?
A) 46,869
B) 159,860
C) 1,115,101
D) 1,321,831
 Which of the following is the value of SSA?
Which of the following is the value of SSA?A) 46,869
B) 159,860
C) 1,115,101
D) 1,321,831

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
69
A market researcher is studying the spending habits of people across age groups. The amount of money spent by each individual is classified by spending category (Dining out, Shopping, or Electronics) - Factor A, and generation (Gen-X, Gen-Y, Gen-Z, or Baby Boomers) - Factor B. An incomplete ANOVA table is shown below.  The p-value for the hypothesis test about factor A is ________.
The p-value for the hypothesis test about factor A is ________.
A) less than 0.01
B) between 0.01 and 0.025
C) between 0.025 and 0.05
D) greater than 0.05
 The p-value for the hypothesis test about factor A is ________.
The p-value for the hypothesis test about factor A is ________.A) less than 0.01
B) between 0.01 and 0.025
C) between 0.025 and 0.05
D) greater than 0.05

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
70
A researcher wants to understand how an annual mortgage payment (in dollars) depends on income level and zonal location using a two-way ANOVA without interaction. The data and an incomplete ANOVA table are shown below. 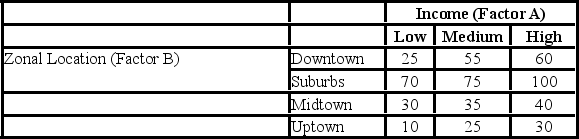
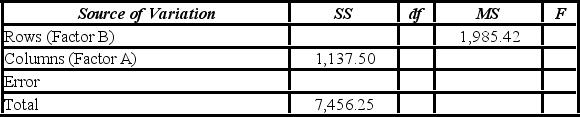 At the 5% significance level, the conclusion for the hypothesis test about factor A is ________.
At the 5% significance level, the conclusion for the hypothesis test about factor A is ________.
A) do not reject the null hypothesis; we can conclude the average mortgage payments differ by income level
B) do not reject the null hypothesis; we cannot conclude the average mortgage payments differ by income level
C) reject the null hypothesis; we can conclude the average mortgage payments differ by income level
D) reject the null hypothesis; we cannot conclude the average mortgage payments differ by income level

 At the 5% significance level, the conclusion for the hypothesis test about factor A is ________.
At the 5% significance level, the conclusion for the hypothesis test about factor A is ________.A) do not reject the null hypothesis; we can conclude the average mortgage payments differ by income level
B) do not reject the null hypothesis; we cannot conclude the average mortgage payments differ by income level
C) reject the null hypothesis; we can conclude the average mortgage payments differ by income level
D) reject the null hypothesis; we cannot conclude the average mortgage payments differ by income level

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
71
A market researcher is studying the spending habits of people across age groups. The amount of money spent by each individual is classified by spending category (Dining out, Shopping, or Electronics) - Factor A, and generation (Gen-X, Gen-Y, Gen-Z, or Baby Boomers) - Factor B. An incomplete ANOVA table is shown below.  At the 5% significance level, the critical value for the hypothesis test about factor A is ________.
At the 5% significance level, the critical value for the hypothesis test about factor A is ________.
A) 2.49
B) 3.32
C) 4.18
D) 5.39
 At the 5% significance level, the critical value for the hypothesis test about factor A is ________.
At the 5% significance level, the critical value for the hypothesis test about factor A is ________.A) 2.49
B) 3.32
C) 4.18
D) 5.39

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
72
A researcher wants to understand how an annual mortgage payment (in dollars) depends on income level and zonal location using a two-way ANOVA without interaction. The data and an incomplete ANOVA table are shown below. 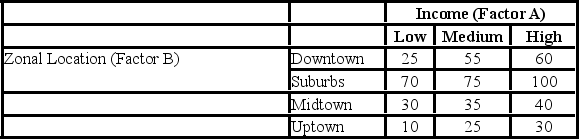
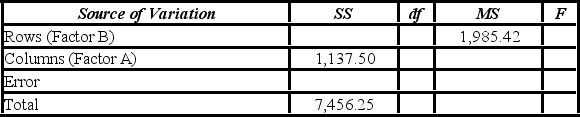 At the 1% significance level, the conclusion for the hypothesis test about factor B is ________.
At the 1% significance level, the conclusion for the hypothesis test about factor B is ________.
A) do not reject the null hypothesis; we can conclude the average mortgage payments differ by zonal location
B) do not reject the null hypothesis; we cannot conclude the average mortgage payments differ by zonal location
C) reject the null hypothesis; we can conclude the average mortgage payments differ by zonal location
D) reject the null hypothesis; we cannot conclude the average mortgage payments differ by zonal location

 At the 1% significance level, the conclusion for the hypothesis test about factor B is ________.
At the 1% significance level, the conclusion for the hypothesis test about factor B is ________.A) do not reject the null hypothesis; we can conclude the average mortgage payments differ by zonal location
B) do not reject the null hypothesis; we cannot conclude the average mortgage payments differ by zonal location
C) reject the null hypothesis; we can conclude the average mortgage payments differ by zonal location
D) reject the null hypothesis; we cannot conclude the average mortgage payments differ by zonal location

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
73
A market researcher is studying the spending habits of people across age groups. The amount of money spent by each individual is classified by spending category (Dining out, Shopping, or Electronics) - Factor A, and generation (Gen-X, Gen-Y, Gen-Z, or Baby Boomers) - Factor B. An incomplete ANOVA table is shown below. 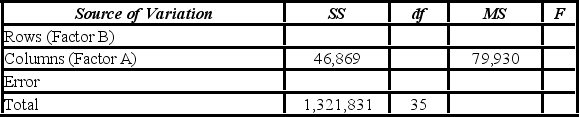 How many degrees of freedom are there for factors A and B?
How many degrees of freedom are there for factors A and B?
A) 2, 3
B) 3, 4
C) 3, 6
D) 2, 4
 How many degrees of freedom are there for factors A and B?
How many degrees of freedom are there for factors A and B?A) 2, 3
B) 3, 4
C) 3, 6
D) 2, 4

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
74
A market researcher is studying the spending habits of people across age groups. The amount of money spent by each individual is classified by spending category (Dining out, Shopping, or Electronics) and generation (Gen-X, Gen-Y, Gen-Z, or Baby Boomers). The data and an incomplete ANOVA table are shown below. 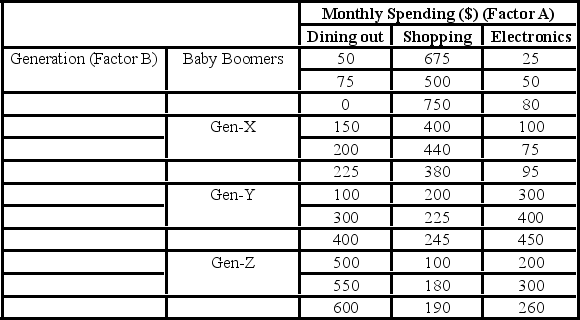
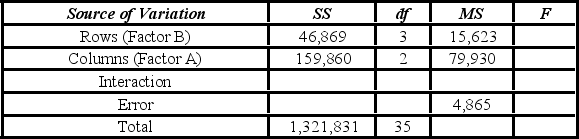 The value of SSE is ________.
The value of SSE is ________.
A) 46,869
B) 159,860
C) 116,767
D) 1,321,831

 The value of SSE is ________.
The value of SSE is ________.A) 46,869
B) 159,860
C) 116,767
D) 1,321,831

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
75
A market researcher is studying the spending habits of people across age groups. The amount of money spent by each individual is classified by spending category (Dining out, Shopping, or Electronics) and generation (Gen-X, Gen-Y, Gen-Z, or Baby Boomers). The data and an incomplete ANOVA table are shown below. 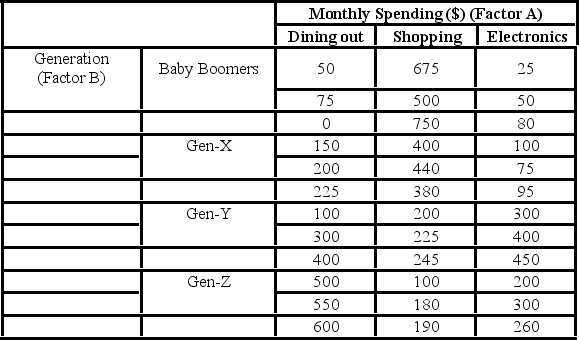
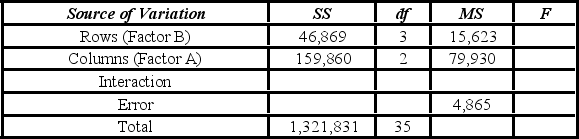 The degrees of freedom for the interaction and the error are ________.
The degrees of freedom for the interaction and the error are ________.
A) 6, 24
B) 6, 30
C) 24, 6
D) 30, 6

 The degrees of freedom for the interaction and the error are ________.
The degrees of freedom for the interaction and the error are ________.A) 6, 24
B) 6, 30
C) 24, 6
D) 30, 6

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
76
A market researcher is studying the spending habits of people across age groups. The amount of money spent by each individual is classified by spending category (Dining out, Shopping, or Electronics) - Factor A, and generation (Gen-X, Gen-Y, Gen-Z, or Baby Boomers) - Factor B. An incomplete ANOVA table is shown below.  Which of the following is the value of MSE?
Which of the following is the value of MSE?
A) 15,623
B) 79,930
C) 37,170
D) 1,321,831
 Which of the following is the value of MSE?
Which of the following is the value of MSE?A) 15,623
B) 79,930
C) 37,170
D) 1,321,831

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
77
A market researcher is studying the spending habits of people across age groups. The amount of money spent by each individual is classified by spending category (Dining out, Shopping, or Electronics) - Factor A, and generation (Gen-X, Gen-Y, Gen-Z, or Baby Boomers) - Factor B. An incomplete ANOVA table is shown below. 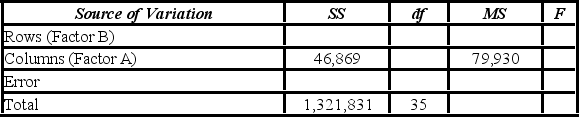 At the 5% significance level, the conclusion of the hypothesis test for factor A is ________.
At the 5% significance level, the conclusion of the hypothesis test for factor A is ________.
A) do not reject the null hypothesis; we cannot conclude the average amount spent differs by spending category
B) do not reject the null hypothesis; we can conclude the average amount spent differs by spending category
C) reject the null hypothesis; we cannot conclude the average amount spent differs by spending category
D) reject the null hypothesis; we can conclude the average amount spent differs by spending category
 At the 5% significance level, the conclusion of the hypothesis test for factor A is ________.
At the 5% significance level, the conclusion of the hypothesis test for factor A is ________.A) do not reject the null hypothesis; we cannot conclude the average amount spent differs by spending category
B) do not reject the null hypothesis; we can conclude the average amount spent differs by spending category
C) reject the null hypothesis; we cannot conclude the average amount spent differs by spending category
D) reject the null hypothesis; we can conclude the average amount spent differs by spending category

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
78
A market researcher is studying the spending habits of people across age groups. The amount of money spent by each individual is classified by spending category (Dining out, Shopping, or Electronics) - Factor A, and generation (Gen-X, Gen-Y, Gen-Z, or Baby Boomers) - Factor B. An incomplete ANOVA table is shown below. 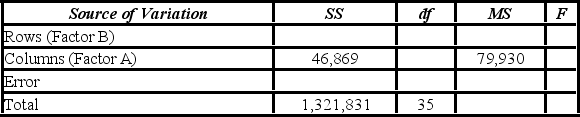 At the 5% significance level, the critical value for the hypothesis test about factor B is ________.
At the 5% significance level, the critical value for the hypothesis test about factor B is ________.
A) 2.28
B) 2.92
C) 3.59
D) 4.51
 At the 5% significance level, the critical value for the hypothesis test about factor B is ________.
At the 5% significance level, the critical value for the hypothesis test about factor B is ________.A) 2.28
B) 2.92
C) 3.59
D) 4.51

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
79
A market researcher is studying the spending habits of people across age groups. The amount of money spent by each individual is classified by spending category (Dining out, Shopping, or Electronics) - Factor A, and generation (Gen-X, Gen-Y, Gen-Z, or Baby Boomers) - Factor B. An incomplete ANOVA table is shown below. 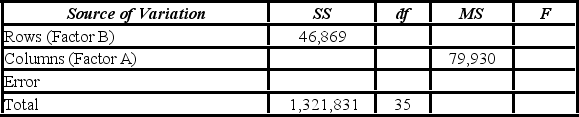 At the 5% significance level, the conclusion of the hypothesis test for Factor B is ________.
At the 5% significance level, the conclusion of the hypothesis test for Factor B is ________.
A) do not reject the null hypothesis; we cannot conclude the average amount spent differs by generation
B) do not reject the null hypothesis; we can conclude the average amount spent differs by generation
C) reject the null hypothesis; we cannot conclude the average amount spent differs by generation
D) reject the null hypothesis; we can conclude the average amount spent differs by generation
 At the 5% significance level, the conclusion of the hypothesis test for Factor B is ________.
At the 5% significance level, the conclusion of the hypothesis test for Factor B is ________.A) do not reject the null hypothesis; we cannot conclude the average amount spent differs by generation
B) do not reject the null hypothesis; we can conclude the average amount spent differs by generation
C) reject the null hypothesis; we cannot conclude the average amount spent differs by generation
D) reject the null hypothesis; we can conclude the average amount spent differs by generation

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck
80
A researcher wants to understand how an annual mortgage payment (in dollars) depends on income level and zonal location using a two-way ANOVA without interaction. The data and an incomplete ANOVA table are shown below. 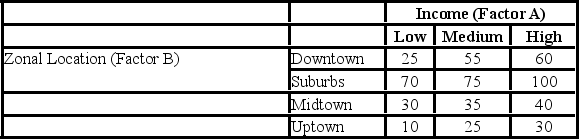
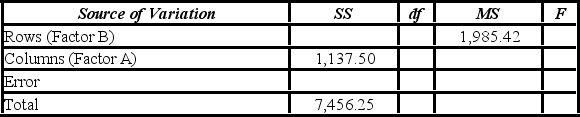 At the 5% significance level, the critical value for the hypothesis test about factor A is ________.
At the 5% significance level, the critical value for the hypothesis test about factor A is ________.
A) 3.46
B) 5.14
C) 7.26
D) 10.92

 At the 5% significance level, the critical value for the hypothesis test about factor A is ________.
At the 5% significance level, the critical value for the hypothesis test about factor A is ________.A) 3.46
B) 5.14
C) 7.26
D) 10.92

Unlock Deck
Unlock for access to all 120 flashcards in this deck.
Unlock Deck
k this deck


