Deck 15: Inference With Regression Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/125
Play
Full screen (f)
Deck 15: Inference With Regression Models
1
The restricted model is a reduced model where the coefficients that are restricted under the null hypothesis are estimated.
False
2
One of the required assumptions of regression analysis states that the error term has a(an) ________ value of zero.
expected
3
The test statistic for a test of individual significance is assumed to have a t distribution with n - k - 2 degrees of freedom, where n is the sample size and k is the number of explanatory variables.
False
4
It is common to refer to the interval estimate for an individual value of y as the ________ interval.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
5
Consider the following simple linear regression model: y = β0 + β1x + ε. When determining whether there is a one-to-one relationship between x and y, the null hypothesis takes the form ________.
A) H0: β1 = 0
B) H0: β1 = 1
C) H0: b1 = 0
D) H0: b1 = 1
A) H0: β1 = 0
B) H0: β1 = 1
C) H0: b1 = 0
D) H0: b1 = 1

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
6
Consider the following simple linear regression model: y = β0 + β1x + ε. When determining whether there is a positive linear relationship between x and y, the alternative hypothesis takes the form ________.
A) HA: β1 = 0
B) HA: β1 > 0
C) HA: β1 < 0
D) HA: b1 > 1
A) HA: β1 = 0
B) HA: β1 > 0
C) HA: β1 < 0
D) HA: b1 > 1

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
7
If the residuals are correlated, then the residuals should show no pattern around the horizontal axis.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
8
The term BLUE stands for Best Linear Unbiased Estimator.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
9
A crucial assumption in a regression model is that the error term is not correlated with any of the explanatory variables.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
10
With the partial F test, we basically analyze the ratio of (SSER - SSEU) to ________.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
11
If in the multiple linear model the slope coefficient βi is negative, it suggests an inverse (negative) relationship between the explanatory variable xi and the response variable y holding the other explanatory variables constant.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
12
Consider the following simple linear regression model: y = β0 + β1x + ε. When determining whether x significantly influences y, the null hypothesis takes the form ________.
A) H0: β1 = 0
B) H0: β1 = 1
C) H0: b1 = 0
D) H0: b1 = 1
A) H0: β1 = 0
B) H0: β1 = 1
C) H0: b1 = 0
D) H0: b1 = 1

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
13
The term multicollinearity refers to the condition when the variance of the error term, conditional on x1, x2, …, xn, is the same for all observations.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
14
The ________ model is a complete model that imposes no restrictions on the coefficients.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
15
If the confidence interval does not contain the value zero, then the ________ variable associated with the regression coefficient is significant.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
16
The F test can be applied for any number of linear restrictions; the resulting test is often referred to as the ________ F test.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
17
When some explanatory variables of a regression model are strongly correlated, this phenomenon is called serial correlation.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
18
________ plots can be used to detect common violations, and they can be used to detect outliers.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
19
Conditional on x1, x2, ..., xk, the error term ε is ________ distributed.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
20
The alternative hypothesis for the test of joint significance is specified as: HA: At least two βj ≠ 0.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
21
Refer to below regression results.  When testing the overall significance of the regression model at the 5%, the decision is to ________.
When testing the overall significance of the regression model at the 5%, the decision is to ________.
A) reject H0; we can conclude that the explanatory variables are jointly significant.
B) not reject H0; we can conclude that the explanatory variables are jointly significant.
C) reject H0; we cannot conclude that the explanatory variables are jointly significant.
D) not reject H0; we cannot conclude the explanatory variables are jointly significant.
 When testing the overall significance of the regression model at the 5%, the decision is to ________.
When testing the overall significance of the regression model at the 5%, the decision is to ________.A) reject H0; we can conclude that the explanatory variables are jointly significant.
B) not reject H0; we can conclude that the explanatory variables are jointly significant.
C) reject H0; we cannot conclude that the explanatory variables are jointly significant.
D) not reject H0; we cannot conclude the explanatory variables are jointly significant.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
22
The accompanying table shows the regression results when estimating y = β0 + β1x + ε  Which of the following is the value of the test statistic when testing whether x significantly influences y?
Which of the following is the value of the test statistic when testing whether x significantly influences y?
A) 0.66
B) 1.42
C) 1.96
D) 2.25
 Which of the following is the value of the test statistic when testing whether x significantly influences y?
Which of the following is the value of the test statistic when testing whether x significantly influences y?A) 0.66
B) 1.42
C) 1.96
D) 2.25

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
23
Refer to the portion of regression results in the accompanying table.  When testing the overall significance of the regression model at the 5% level given a critical value of F0.05,(2,20) = 3.49, the decision is to ________.
When testing the overall significance of the regression model at the 5% level given a critical value of F0.05,(2,20) = 3.49, the decision is to ________.
A) reject H0; we can conclude that the explanatory variables are jointly significant.
B) not reject H0; we can conclude that the explanatory variables are jointly significant.
C) reject H0; we cannot conclude that the explanatory variables are jointly significant.
D) not reject H0; we cannot conclude the explanatory variables are jointly significant.
 When testing the overall significance of the regression model at the 5% level given a critical value of F0.05,(2,20) = 3.49, the decision is to ________.
When testing the overall significance of the regression model at the 5% level given a critical value of F0.05,(2,20) = 3.49, the decision is to ________.A) reject H0; we can conclude that the explanatory variables are jointly significant.
B) not reject H0; we can conclude that the explanatory variables are jointly significant.
C) reject H0; we cannot conclude that the explanatory variables are jointly significant.
D) not reject H0; we cannot conclude the explanatory variables are jointly significant.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
24
When testing r linear restrictions imposed on the model y = β0 + β1x1 + ... + βk xk + ε, the test statistic is assumed to follow the 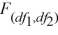 distribution with ________.
distribution with ________.
A) df1 = k and df2 = n - k - 1
B) df1 = k - 1 and df2 = n - k - 1
C) df1 = r and df2 = n - k
D) df1 = r and df2 = n - k - 1
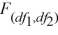 distribution with ________.
distribution with ________.A) df1 = k and df2 = n - k - 1
B) df1 = k - 1 and df2 = n - k - 1
C) df1 = r and df2 = n - k
D) df1 = r and df2 = n - k - 1

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
25
In regression, the two types of interval estimates concerning y are called ________.
A) significance interval and prediction interval
B) confidence interval and significance interval
C) confidence interval and prediction interval
D) significance interval and frequency interval
A) significance interval and prediction interval
B) confidence interval and significance interval
C) confidence interval and prediction interval
D) significance interval and frequency interval

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
26
Given the following portion of regression results, which of the following is the value of the F2,20 test statistic? 
A) 1.96
B) 3.49
C) 8.04
D) 10

A) 1.96
B) 3.49
C) 8.04
D) 10

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
27
The accompanying table shows the regression results when estimating y = β0 + β1x + ε.  When testing whether the slope coefficient differs from 1, the value of the test statistic is ________.
When testing whether the slope coefficient differs from 1, the value of the test statistic is ________.
A) 0.66
B) 1.42
C) 1.96
D) 2.25
 When testing whether the slope coefficient differs from 1, the value of the test statistic is ________.
When testing whether the slope coefficient differs from 1, the value of the test statistic is ________.A) 0.66
B) 1.42
C) 1.96
D) 2.25

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
28
Given the following portion of regression results, which of the following is the value of the F(2,20) test statistic? 
A) 1.96
B) 2.59
C) 3.49
D) 10

A) 1.96
B) 2.59
C) 3.49
D) 10

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
29
When estimating y = β0 + β1x1 + β2x2 + β3x3 + ε, you wish to test H0: β1 = β2 = 0 versus 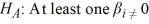 . The value of the test statistic is F(2,20) = 2.50 and its associated p-value is 0.1073. At the 5% significance level, the conclusion is to ________.
. The value of the test statistic is F(2,20) = 2.50 and its associated p-value is 0.1073. At the 5% significance level, the conclusion is to ________.
A) reject the null hypothesis; we can conclude that x1 and x2 are jointly significant
B) reject the null hypothesis; we cannot conclude that x1 and x2 are jointly significant
C) not reject the null hypothesis; we can conclude that x1 and x2 are jointly significant
D) not reject the null hypothesis; we cannot conclude that x1 and x2 are jointly significant
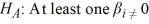 . The value of the test statistic is F(2,20) = 2.50 and its associated p-value is 0.1073. At the 5% significance level, the conclusion is to ________.
. The value of the test statistic is F(2,20) = 2.50 and its associated p-value is 0.1073. At the 5% significance level, the conclusion is to ________.A) reject the null hypothesis; we can conclude that x1 and x2 are jointly significant
B) reject the null hypothesis; we cannot conclude that x1 and x2 are jointly significant
C) not reject the null hypothesis; we can conclude that x1 and x2 are jointly significant
D) not reject the null hypothesis; we cannot conclude that x1 and x2 are jointly significant

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
30
A sample of 200 monthly observations is used to run a simple linear regression: Returns = β0 + β1 Leverage + ε. A 5% level of significance is used to study if leverage has a significant influence on returns. The value of the test statistic for the regression coefficient of Leverage is calculated as t198 = -1.09, with an associated p-value of 0.2770. The correct decision is to ________.
A) reject the null hypothesis; we can conclude that leverage significantly explains returns
B) reject the null hypothesis; we cannot conclude that leverage significantly explains returns
C) not reject the null hypothesis; we cannot conclude that leverage significantly explains returns
D) not reject the null hypothesis; we can conclude that leverage significantly explains returns
A) reject the null hypothesis; we can conclude that leverage significantly explains returns
B) reject the null hypothesis; we cannot conclude that leverage significantly explains returns
C) not reject the null hypothesis; we cannot conclude that leverage significantly explains returns
D) not reject the null hypothesis; we can conclude that leverage significantly explains returns

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
31
Excel and virtually all other statistical packages report the p-value ________.
A) for a two-tailed test that assesses whether the regression coefficient differs from one
B) for a right-tailed test that assesses whether the regression coefficient is greater than zero
C) for a two-tailed test that assesses whether the regression coefficient differs from zero
D) for a left-tailed test that assesses whether the regression coefficient is less than zero
A) for a two-tailed test that assesses whether the regression coefficient differs from one
B) for a right-tailed test that assesses whether the regression coefficient is greater than zero
C) for a two-tailed test that assesses whether the regression coefficient differs from zero
D) for a left-tailed test that assesses whether the regression coefficient is less than zero

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
32
The accompanying table shows the regression results when estimating y = β0 + β1x + ε.  Is x significantly related to y at the 5% significance level?
Is x significantly related to y at the 5% significance level?
A) Yes, because the p-value of 0.0745 is greater than 0.05.
B) No, because the p-value of 0.0745 is greater than 0.05.
C) Yes, because the slope coefficient of 1.417 is less than the test statistic of 2.25.
D) No, because the slope coefficient of 1.417 is less than the test statistic of 2.25.
 Is x significantly related to y at the 5% significance level?
Is x significantly related to y at the 5% significance level?A) Yes, because the p-value of 0.0745 is greater than 0.05.
B) No, because the p-value of 0.0745 is greater than 0.05.
C) Yes, because the slope coefficient of 1.417 is less than the test statistic of 2.25.
D) No, because the slope coefficient of 1.417 is less than the test statistic of 2.25.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
33
The accompanying table shows the regression results when estimating y = β0 + β1x1 + β2x2 + β3x3 + ε. 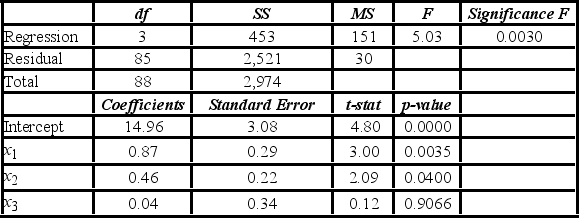 At the 5% significance level, which of the following explanatory variable(s) is(are) individually significant?
At the 5% significance level, which of the following explanatory variable(s) is(are) individually significant?
A) Only x1
B) Only x3
C) x1 and x2
D) x2 and x3
 At the 5% significance level, which of the following explanatory variable(s) is(are) individually significant?
At the 5% significance level, which of the following explanatory variable(s) is(are) individually significant?A) Only x1
B) Only x3
C) x1 and x2
D) x2 and x3

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
34
Given the following portion of regression results, which of the following conclusions is true with regard to the F test at the 5% significance level? 
A) Neither of the explanatory variables is related to the response variable.
B) Both of the explanatory variables are related to the response variable.
C) Exactly one of the explanatory variables is related to the response variable.
D) At least one of the explanatory variables is significantly related to the response variable.

A) Neither of the explanatory variables is related to the response variable.
B) Both of the explanatory variables are related to the response variable.
C) Exactly one of the explanatory variables is related to the response variable.
D) At least one of the explanatory variables is significantly related to the response variable.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
35
Which of the following is the 95% confidence interval for the regression coefficient β1, if df = 30, b1 = −2 and s ![<strong>Which of the following is the 95% confidence interval for the regression coefficient β<sub>1</sub>, if df = 30, b<sub>1</sub> = −2 and s = 3?</strong> A) [−5.00, −1.00] B) [−7.88, 3.88] C) [−7.09, 3.09] D) [−8.13, 4.13]](https://storage.examlex.com/TB6618/11ea8309_a964_c80a_b223_b3f7cf1407ec_TB6618_11.jpg) = 3?
= 3?
A) [−5.00, −1.00]
B) [−7.88, 3.88]
C) [−7.09, 3.09]
D) [−8.13, 4.13]
![<strong>Which of the following is the 95% confidence interval for the regression coefficient β<sub>1</sub>, if df = 30, b<sub>1</sub> = −2 and s = 3?</strong> A) [−5.00, −1.00] B) [−7.88, 3.88] C) [−7.09, 3.09] D) [−8.13, 4.13]](https://storage.examlex.com/TB6618/11ea8309_a964_c80a_b223_b3f7cf1407ec_TB6618_11.jpg) = 3?
= 3?A) [−5.00, −1.00]
B) [−7.88, 3.88]
C) [−7.09, 3.09]
D) [−8.13, 4.13]

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
36
Refer to below regression results.  When testing the overall significance of the regression model at the 5% level given a critical value of F0.05,(2.20) = 3.49, the decision is to ________.
When testing the overall significance of the regression model at the 5% level given a critical value of F0.05,(2.20) = 3.49, the decision is to ________.
A) reject H0; we can conclude that the explanatory variables are jointly significant.
B) not reject H0; we can conclude that the explanatory variables are jointly significant.
C) reject H0; we cannot conclude that the explanatory variables are jointly significant.
D) not reject H0; we cannot conclude the explanatory variables are jointly significant.
 When testing the overall significance of the regression model at the 5% level given a critical value of F0.05,(2.20) = 3.49, the decision is to ________.
When testing the overall significance of the regression model at the 5% level given a critical value of F0.05,(2.20) = 3.49, the decision is to ________.A) reject H0; we can conclude that the explanatory variables are jointly significant.
B) not reject H0; we can conclude that the explanatory variables are jointly significant.
C) reject H0; we cannot conclude that the explanatory variables are jointly significant.
D) not reject H0; we cannot conclude the explanatory variables are jointly significant.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
37
When estimating y = β0 + β1x1 + β2x2 + β3x3 + ε, you wish to test H0: β1 = β2 versus HA: β1 ≠ β2. The value of the test statistic is F(1,30) = 7.75 and its associated p-value is 0.0092. At the 1% significance level, the conclusion is to ________.
A) reject the null hypothesis; we cannot conclude that the influence of x1 on y is different from the influence of x2 on y.
B) reject the null hypothesis; we can conclude that the influence of x1 on y is different from the influence of x2 on y.
C) not reject the null hypothesis; we can conclude that the influence of x1 on y is different from the influence of x2 on y.
D) not reject the null hypothesis; we cannot conclude that the influence of x1 on y is different from the influence of x2 on y.
A) reject the null hypothesis; we cannot conclude that the influence of x1 on y is different from the influence of x2 on y.
B) reject the null hypothesis; we can conclude that the influence of x1 on y is different from the influence of x2 on y.
C) not reject the null hypothesis; we can conclude that the influence of x1 on y is different from the influence of x2 on y.
D) not reject the null hypothesis; we cannot conclude that the influence of x1 on y is different from the influence of x2 on y.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
38
For a given confidence level, the prediction interval is always wider than the confidence interval because ________.
A) the confidence interval is for a particular value of y rather than for the expected value E(y)
B) the prediction interval is for a particular value of y rather than for the expected value E(y)
C) the confidence interval is for a particular value of x rather than for the expected value E(x)
D) the prediction interval is for a particular value of x rather than for the expected value E(x)
A) the confidence interval is for a particular value of y rather than for the expected value E(y)
B) the prediction interval is for a particular value of y rather than for the expected value E(y)
C) the confidence interval is for a particular value of x rather than for the expected value E(x)
D) the prediction interval is for a particular value of x rather than for the expected value E(x)

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
39
Consider the following simple linear regression model: y = β0 + β1x + ε. When determining whether there is a negative linear relationship between x and y, the alternative hypothesis takes the form ________.
A) HA: β1 = 0
B) HA: β1 > 0
C) HA: β1 < 0
D) HA: b1 > 0
A) HA: β1 = 0
B) HA: β1 > 0
C) HA: β1 < 0
D) HA: b1 > 0

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
40
In regression, the predicted values concerning y are subject to ________.
A) kurtosis
B) skewness
C) mean deviation
D) sampling variation
A) kurtosis
B) skewness
C) mean deviation
D) sampling variation

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
41
A researcher analyzes the factors that may influence amusement park attendance. She estimates the following model: Attendance = β0 + β1Price + β2Temperature + β3Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), Temperature is the average daily temperature (in °F), and Rides is the number of rides at the amusement park. A portion of the regression results is shown in the accompanying table. 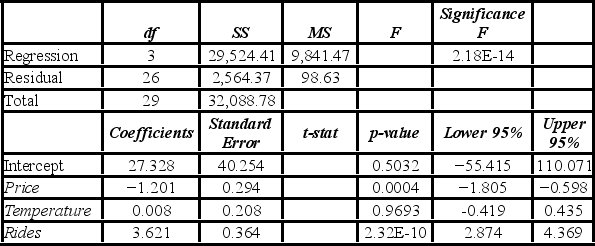 When testing whether Temperature is significant at the 5% significance level, she ________.
When testing whether Temperature is significant at the 5% significance level, she ________.
A) rejects H0: β2 = 0, and concludes that Temperature is significant
B) does not reject H0: β2 = 0, and concludes that Temperature is significant
C) rejects H0: β2 = 0, and cannot conclude that Temperature is significant
D) does not reject H0: β2 = 0, and cannot conclude that Temperature is significant
 When testing whether Temperature is significant at the 5% significance level, she ________.
When testing whether Temperature is significant at the 5% significance level, she ________.A) rejects H0: β2 = 0, and concludes that Temperature is significant
B) does not reject H0: β2 = 0, and concludes that Temperature is significant
C) rejects H0: β2 = 0, and cannot conclude that Temperature is significant
D) does not reject H0: β2 = 0, and cannot conclude that Temperature is significant

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
42
Which of the following violates the assumptions of regression analysis?
A) The error term is normally distributed.
B) The error term has a zero mean.
C) The error term is correlated with an explanatory variable.
D) The error term has a constant variance.
A) The error term is normally distributed.
B) The error term has a zero mean.
C) The error term is correlated with an explanatory variable.
D) The error term has a constant variance.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
43
A marketing analyst wants to examine the relationship between sales (in $1,000s) and advertising (in $100s) for firms in the food and beverage industry and so collects monthly data for 25 firms. He estimates the model: Sales = β0 + β1 Advertising + ε. The following table shows a portion of the regression results.  Which of the following are the competing hypotheses used to test whether Advertising is significant in predicting Sales?
Which of the following are the competing hypotheses used to test whether Advertising is significant in predicting Sales?
A) H0: b1 = 0; HA: b1 ≠ 0.
B) H0: b1 = 2.88; HA: b1 ≠ 2.88.
C) H0: β1 = 0; HA: β1 ≠ 0.
D) H0: β1 ≠ 0; HA: β1 = 0.
 Which of the following are the competing hypotheses used to test whether Advertising is significant in predicting Sales?
Which of the following are the competing hypotheses used to test whether Advertising is significant in predicting Sales?A) H0: b1 = 0; HA: b1 ≠ 0.
B) H0: b1 = 2.88; HA: b1 ≠ 2.88.
C) H0: β1 = 0; HA: β1 ≠ 0.
D) H0: β1 ≠ 0; HA: β1 = 0.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
44
A marketing analyst wants to examine the relationship between sales (in $1,000s) and advertising (in $100s) for firms in the food and beverage industry and so collects monthly data for 25 firms. He estimates the model: Sales = β0 + β1 Advertising + ε. The following table shows a portion of the regression results.  When testing whether the slope coefficient differs from 3, the value of the test statistic is ________.
When testing whether the slope coefficient differs from 3, the value of the test statistic is ________.
A) t23 = -1.895
B) t23 = -0.079
C) t23 = 0.079
D) t23 = 1.895
 When testing whether the slope coefficient differs from 3, the value of the test statistic is ________.
When testing whether the slope coefficient differs from 3, the value of the test statistic is ________.A) t23 = -1.895
B) t23 = -0.079
C) t23 = 0.079
D) t23 = 1.895

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
45
A sports analyst wants to exam the factors that may influence a tennis player's chances of winning. Over four tournaments, he collects data on 30 tennis players and estimates the following model: Win = β0 + β1Double Faults + β2Aces + ε, where Win is the proportion of winning, Double Faults is the percentage of double faults made, and Aces is the number of aces. A portion of the regression results are shown in the accompanying table. 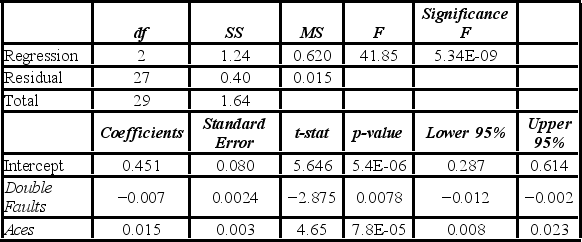 When testing whether the explanatory variables are jointly significant at the 5% significance level, he ________.
When testing whether the explanatory variables are jointly significant at the 5% significance level, he ________.
A) rejects H0, and concludes that the explanatory variables are jointly significant
B) does not reject H0, and concludes that the explanatory variables are jointly significant
C) rejects H0, and cannot concludes that the explanatory variables are jointly significant
D) does not reject H0, and cannot conclude that the explanatory variables are jointly significant
 When testing whether the explanatory variables are jointly significant at the 5% significance level, he ________.
When testing whether the explanatory variables are jointly significant at the 5% significance level, he ________.A) rejects H0, and concludes that the explanatory variables are jointly significant
B) does not reject H0, and concludes that the explanatory variables are jointly significant
C) rejects H0, and cannot concludes that the explanatory variables are jointly significant
D) does not reject H0, and cannot conclude that the explanatory variables are jointly significant

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
46
When confronted with multicollinearity, a good remedy is to ________ if we can justify its redundancy.
A) add one more collinear variable
B) drop one of the collinear variables
C) remove both the collinear variables
D) add as many collinear variables as possible
A) add one more collinear variable
B) drop one of the collinear variables
C) remove both the collinear variables
D) add as many collinear variables as possible

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
47
Serial correlation is typically observed in ________.
A) outliers
B) sparse data
C) time series data
D) get estimators that are biased and cannot conduct tests of significance
A) outliers
B) sparse data
C) time series data
D) get estimators that are biased and cannot conduct tests of significance

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
48
In regression, multicollinearity is considered problematic when two or more explanatory variables are ________.
A) not correlated
B) rarely correlated
C) highly correlated
D) moderately correlated
A) not correlated
B) rarely correlated
C) highly correlated
D) moderately correlated

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
49
A sports analyst wants to exam the factors that may influence a tennis player's chances of winning. Over four tournaments, he collects data on 30 tennis players and estimates the following model: Win = β0 + β1 Double Faults + β2Aces + ε, where Win is the proportion of winning, Double Faults is the percentage of double faults made, and Aces is the number of aces. A portion of the regression results are shown in the accompanying table. ![<strong>A sports analyst wants to exam the factors that may influence a tennis player's chances of winning. Over four tournaments, he collects data on 30 tennis players and estimates the following model: Win = β<sub>0</sub> + β<sub>1</sub> Double Faults + β<sub>2</sub>Aces + ε, where Win is the proportion of winning, Double Faults is the percentage of double faults made, and Aces is the number of aces. A portion of the regression results are shown in the accompanying table. Excel shows that the 95% confidence interval for β<sub>1</sub> is [−0.12, −0.002]. When determining whether or not Double Faults is significant at the 5% significance level, he ________.</strong> A) rejects H<sub>0</sub>: β<sub>1</sub> = 0, and concludes that DoubleFaults is significant B) does not reject H<sub>0</sub>: β<sub>1</sub> = 0, and concludes that DoubleFaults is significant C) rejects H<sub>0</sub>: β<sub>1</sub> = 0, and cannot conclude that DoubleFaults is significant D) does not reject H<sub>0</sub>: β<sub>1</sub> = 0, and cannot concludes DoubleFaults is significant](https://storage.examlex.com/TB6618/11ea8309_a96a_1f4e_b223_e98725363ad6_TB6618_00.jpg) Excel shows that the 95% confidence interval for β1 is [−0.12, −0.002]. When determining whether or not Double Faults is significant at the 5% significance level, he ________.
Excel shows that the 95% confidence interval for β1 is [−0.12, −0.002]. When determining whether or not Double Faults is significant at the 5% significance level, he ________.
A) rejects H0: β1 = 0, and concludes that DoubleFaults is significant
B) does not reject H0: β1 = 0, and concludes that DoubleFaults is significant
C) rejects H0: β1 = 0, and cannot conclude that DoubleFaults is significant
D) does not reject H0: β1 = 0, and cannot concludes DoubleFaults is significant
![<strong>A sports analyst wants to exam the factors that may influence a tennis player's chances of winning. Over four tournaments, he collects data on 30 tennis players and estimates the following model: Win = β<sub>0</sub> + β<sub>1</sub> Double Faults + β<sub>2</sub>Aces + ε, where Win is the proportion of winning, Double Faults is the percentage of double faults made, and Aces is the number of aces. A portion of the regression results are shown in the accompanying table. Excel shows that the 95% confidence interval for β<sub>1</sub> is [−0.12, −0.002]. When determining whether or not Double Faults is significant at the 5% significance level, he ________.</strong> A) rejects H<sub>0</sub>: β<sub>1</sub> = 0, and concludes that DoubleFaults is significant B) does not reject H<sub>0</sub>: β<sub>1</sub> = 0, and concludes that DoubleFaults is significant C) rejects H<sub>0</sub>: β<sub>1</sub> = 0, and cannot conclude that DoubleFaults is significant D) does not reject H<sub>0</sub>: β<sub>1</sub> = 0, and cannot concludes DoubleFaults is significant](https://storage.examlex.com/TB6618/11ea8309_a96a_1f4e_b223_e98725363ad6_TB6618_00.jpg) Excel shows that the 95% confidence interval for β1 is [−0.12, −0.002]. When determining whether or not Double Faults is significant at the 5% significance level, he ________.
Excel shows that the 95% confidence interval for β1 is [−0.12, −0.002]. When determining whether or not Double Faults is significant at the 5% significance level, he ________.A) rejects H0: β1 = 0, and concludes that DoubleFaults is significant
B) does not reject H0: β1 = 0, and concludes that DoubleFaults is significant
C) rejects H0: β1 = 0, and cannot conclude that DoubleFaults is significant
D) does not reject H0: β1 = 0, and cannot concludes DoubleFaults is significant

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
50
A researcher gathers data on 25 households and estimates the following model: Expenditure = β0 + β1 Income + ε. A residual plot of the estimated model is shown in the accompanying graph. 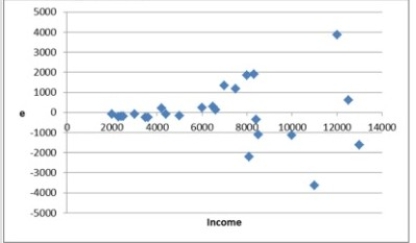 Which of the following can be inferred from the residual plot?
Which of the following can be inferred from the residual plot?
A) The residuals have little variation.
B) The residuals do not exhibit any pattern.
C) The residuals seem to fan out across the horizontal axis.
D) The residuals are evenly distributed across the horizontal axis.
 Which of the following can be inferred from the residual plot?
Which of the following can be inferred from the residual plot?A) The residuals have little variation.
B) The residuals do not exhibit any pattern.
C) The residuals seem to fan out across the horizontal axis.
D) The residuals are evenly distributed across the horizontal axis.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
51
A marketing analyst wants to examine the relationship between sales (in $1,000s) and advertising (in $100s) for firms in the food and beverage industry and so collects monthly data for 25 firms. He estimates the model: Sales = β0 + β1 Advertising + ε. The following table shows a portion of the regression results.  When testing whether Advertising is significant at the 10% significance level, the conclusion is to ________.
When testing whether Advertising is significant at the 10% significance level, the conclusion is to ________.
A) reject H0; we can conclude advertising is significant
B) not reject H0; we cannot conclude advertising is significant
C) reject H0; we cannot conclude advertising is significant
D) not reject H0; we can conclude advertising is significant
 When testing whether Advertising is significant at the 10% significance level, the conclusion is to ________.
When testing whether Advertising is significant at the 10% significance level, the conclusion is to ________.A) reject H0; we can conclude advertising is significant
B) not reject H0; we cannot conclude advertising is significant
C) reject H0; we cannot conclude advertising is significant
D) not reject H0; we can conclude advertising is significant

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
52
Serial correlation occurs when the error term is ________.
A) dispersed evenly
B) randomly distributed
C) correlated across observations
D) uncorrelated across observations
A) dispersed evenly
B) randomly distributed
C) correlated across observations
D) uncorrelated across observations

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
53
One of the assumptions of regression analysis is ________.
A) there is perfect multicollinearity among some explanatory variables
B) there is no perfect multicollinearity among any explanatory variables
C) there is some degree of multicollinearity among some explanatory variables
D) None of these choices is correct.
A) there is perfect multicollinearity among some explanatory variables
B) there is no perfect multicollinearity among any explanatory variables
C) there is some degree of multicollinearity among some explanatory variables
D) None of these choices is correct.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
54
A marketing analyst wants to examine the relationship between sales (in $1,000s) and advertising (in $100s) for firms in the food and beverage industry and so collects monthly data for 25 firms. He estimates the model: Sales = β0 + β1 Advertising + ε. The following table shows a portion of the regression results.  When testing whether the slope coefficient differs from 3, the critical values at the 5% significance level are −2.069 and 2.069. The conclusion to the test is to ________.
When testing whether the slope coefficient differs from 3, the critical values at the 5% significance level are −2.069 and 2.069. The conclusion to the test is to ________.
A) reject H0; we can conclude the slope coefficient differs from 3
B) not reject H0; we can conclude the slope coefficient differs from 3
C) reject H0; we cannot conclude the slope coefficient differs from 3
D) not reject H0; we cannot conclude the slope coefficient differs from 3
 When testing whether the slope coefficient differs from 3, the critical values at the 5% significance level are −2.069 and 2.069. The conclusion to the test is to ________.
When testing whether the slope coefficient differs from 3, the critical values at the 5% significance level are −2.069 and 2.069. The conclusion to the test is to ________.A) reject H0; we can conclude the slope coefficient differs from 3
B) not reject H0; we can conclude the slope coefficient differs from 3
C) reject H0; we cannot conclude the slope coefficient differs from 3
D) not reject H0; we cannot conclude the slope coefficient differs from 3

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
55
A sports analyst wants to exam the factors that may influence a tennis player's chances of winning. Over four tournaments, he collects data on 30 tennis players and estimates the following model: Win = β0 + β1Double Faults + β2Aces + ε, where Win is the proportion of winning, Double Faults is the percentage of double faults made, and Aces is the number of aces. A portion of the regression results are shown in the accompanying table. 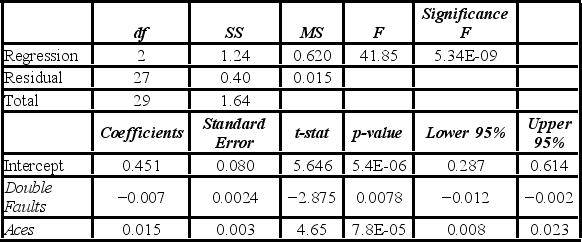 When testing whether the explanatory variables jointly influence the response variable, the null hypothesis is ________.
When testing whether the explanatory variables jointly influence the response variable, the null hypothesis is ________.
A) H0: β1 = β2 = 0
B) H0: β1 + β2 = 0
C) H0: β0 = β1 = β2 = 0
D) H0: β0 + β1 + β2 + 0
 When testing whether the explanatory variables jointly influence the response variable, the null hypothesis is ________.
When testing whether the explanatory variables jointly influence the response variable, the null hypothesis is ________.A) H0: β1 = β2 = 0
B) H0: β1 + β2 = 0
C) H0: β0 = β1 = β2 = 0
D) H0: β0 + β1 + β2 + 0

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
56
A marketing analyst wants to examine the relationship between sales (in $1,000s) and advertising (in $100s) for firms in the food and beverage industry and collects monthly data for 25 firms. He estimates the model: Sales = β0 + β1 Advertising + ε. The following table shows a portion of the regression results.  Which of the following are the competing hypotheses used to test whether the slope coefficient differs from 3?
Which of the following are the competing hypotheses used to test whether the slope coefficient differs from 3?
A) H0: b1 = 3; HA: b1 ≠ 3
B) H0: b1 = 2.88; HA: b1 ≠ 2.88
C) H0: β1 = 3; HA: β1 ≠ 3
D) H0: β1 = 2.88; HA: β1 ≠ 2.88
 Which of the following are the competing hypotheses used to test whether the slope coefficient differs from 3?
Which of the following are the competing hypotheses used to test whether the slope coefficient differs from 3?A) H0: b1 = 3; HA: b1 ≠ 3
B) H0: b1 = 2.88; HA: b1 ≠ 2.88
C) H0: β1 = 3; HA: β1 ≠ 3
D) H0: β1 = 2.88; HA: β1 ≠ 2.88

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
57
A sports analyst wants to exam the factors that may influence a tennis player's chances of winning. Over four tournaments, he collects data on 30 tennis players and estimates the following model: Win = β0 + β1 Double Faults + β2Aces + ε, where Win is the proportion of winning, Double Faults is the percentage of double faults made, and Aces is the number of aces. A portion of the regression results are shown in the accompanying table. 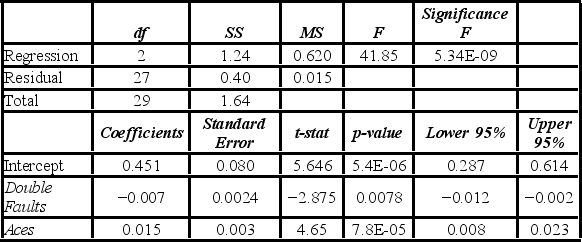 Is the relationship between Win and Aces significant at the 5% significance level?
Is the relationship between Win and Aces significant at the 5% significance level?
A) No, because the relevant p-value is less than 0.05.
B) Yes, because the relevant p-value is less than 0.05.
C) No, because the relevant p-value is greater than 0.05.
D) Yes, because the relevant p-value is greater than 0.05.
 Is the relationship between Win and Aces significant at the 5% significance level?
Is the relationship between Win and Aces significant at the 5% significance level?A) No, because the relevant p-value is less than 0.05.
B) Yes, because the relevant p-value is less than 0.05.
C) No, because the relevant p-value is greater than 0.05.
D) Yes, because the relevant p-value is greater than 0.05.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
58
Multicollinearity is suspected when ________.
A) there is a low R2 coupled with significant explanatory variables
B) there is a high R2 coupled with significant explanatory variables
C) there is a low R2 coupled with insignificant explanatory variables
D) there is a high R2 coupled with insignificant explanatory variables
A) there is a low R2 coupled with significant explanatory variables
B) there is a high R2 coupled with significant explanatory variables
C) there is a low R2 coupled with insignificant explanatory variables
D) there is a high R2 coupled with insignificant explanatory variables

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
59
A researcher analyzes the factors that may influence amusement park attendance. She estimates the following model: Attendance = β0 + β1 Price + β2 Temperature + β3 Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), Temperature is the average daily temperature (in oF), and Rides is the number of rides at the amusement park. A portion of the regression results is shown in the accompanying table. 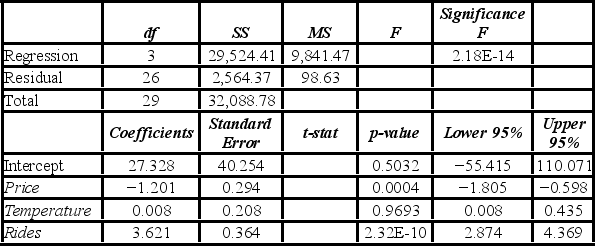 When testing whether Price is significant in explaining Attendance, the value of the test statistic is ________.
When testing whether Price is significant in explaining Attendance, the value of the test statistic is ________.
A) −4.085.
B) −1.201.
C) 1.201.
D) 4.085.
 When testing whether Price is significant in explaining Attendance, the value of the test statistic is ________.
When testing whether Price is significant in explaining Attendance, the value of the test statistic is ________.A) −4.085.
B) −1.201.
C) 1.201.
D) 4.085.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
60
If the variance of the error term is not the same for all observations, we ________.
A) get estimators that are biased
B) can perform tests of significance
C) cannot conduct tests of significance
D) Both get estimators that are biased and cannot conduct tests of significance are correct.
A) get estimators that are biased
B) can perform tests of significance
C) cannot conduct tests of significance
D) Both get estimators that are biased and cannot conduct tests of significance are correct.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
61
Tiffany & Co. has been the world's premier jeweler since 1837. The performance of Tiffany's stock is likely to be strongly influenced by the economy. Monthly data for Tiffany's risk-adjusted return and the risk-adjusted market return are collected for a five-year period (n = 60). The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.  You would like to determine whether an investment in Tiffany's is riskier than the market. When conducting this test, you set up the following competing hypotheses: ________.
You would like to determine whether an investment in Tiffany's is riskier than the market. When conducting this test, you set up the following competing hypotheses: ________.
A) H0: α = 0; HA: α ≠ 0.
B) H0: β = 0; HA: β ≠ 0
C) H0: α ≤ 1; HA: α > 1
D) H0: β ≤ 1; HA: β > 1
 You would like to determine whether an investment in Tiffany's is riskier than the market. When conducting this test, you set up the following competing hypotheses: ________.
You would like to determine whether an investment in Tiffany's is riskier than the market. When conducting this test, you set up the following competing hypotheses: ________.A) H0: α = 0; HA: α ≠ 0.
B) H0: β = 0; HA: β ≠ 0
C) H0: α ≤ 1; HA: α > 1
D) H0: β ≤ 1; HA: β > 1

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
62
The accompanying table shows the regression results when estimating y = β0 + β1x1 + β2x2 + β3x3 + ε. 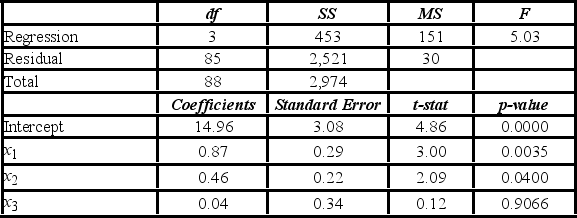 When testing whether or not x1 and x2 are jointly significant, the null hypothesis is ________.
When testing whether or not x1 and x2 are jointly significant, the null hypothesis is ________.
A) H0: β1 = β2
B) H0: β1 ≠ β2
C) H0: β1 + β2 = 0
D) H0: β1 = β2 = 0
 When testing whether or not x1 and x2 are jointly significant, the null hypothesis is ________.
When testing whether or not x1 and x2 are jointly significant, the null hypothesis is ________.A) H0: β1 = β2
B) H0: β1 ≠ β2
C) H0: β1 + β2 = 0
D) H0: β1 = β2 = 0

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
63
The accompanying table shows the regression results when estimating y = β0 + β1x1 + β2x2 + β3x3 + ε. 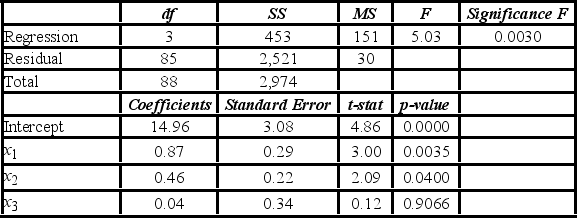 At the 5% significance level, which of the following explanatory variable(s) is(are) individually significant?
At the 5% significance level, which of the following explanatory variable(s) is(are) individually significant?
A) Only x1
B) Only x3
C) x1 and x2
D) x2 and x3
 At the 5% significance level, which of the following explanatory variable(s) is(are) individually significant?
At the 5% significance level, which of the following explanatory variable(s) is(are) individually significant?A) Only x1
B) Only x3
C) x1 and x2
D) x2 and x3

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
64
A researcher analyzes the factors that may influence amusement park attendance. She estimates the following model: Attendance = β0 + β1Price + β2Temperature + β3Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), Temperature is the average daily temperature (in °F), and Rides is the number of rides at the amusement park. A portion of the regression results is shown in the accompanying table. 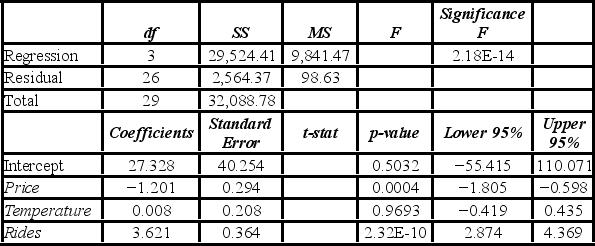 When testing whether the explanatory variables Temperature and Rides are jointly significant, the p-value associated with the test is 0.0000. At the 1% significance level, the researcher ________.
When testing whether the explanatory variables Temperature and Rides are jointly significant, the p-value associated with the test is 0.0000. At the 1% significance level, the researcher ________.
A) rejects H0, and concludes that at least one of the explanatory variables, Temperature and Rides, is significant in explaining Attendance
B) does not reject H0, and concludes that at least one of the explanatory variables, Temperature and Rides, is significant in explaining Attendance
C) rejects H0, and cannot conclude that at least one of the explanatory variables, Temperature and Rides, is significant in explaining Attendance
D) does not reject H0, and cannot conclude at least one of the explanatory variables, Temperature and Rides, is significant in explaining Attendance
 When testing whether the explanatory variables Temperature and Rides are jointly significant, the p-value associated with the test is 0.0000. At the 1% significance level, the researcher ________.
When testing whether the explanatory variables Temperature and Rides are jointly significant, the p-value associated with the test is 0.0000. At the 1% significance level, the researcher ________.A) rejects H0, and concludes that at least one of the explanatory variables, Temperature and Rides, is significant in explaining Attendance
B) does not reject H0, and concludes that at least one of the explanatory variables, Temperature and Rides, is significant in explaining Attendance
C) rejects H0, and cannot conclude that at least one of the explanatory variables, Temperature and Rides, is significant in explaining Attendance
D) does not reject H0, and cannot conclude at least one of the explanatory variables, Temperature and Rides, is significant in explaining Attendance

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
65
Tiffany & Co. has been the world's premier jeweler since 1837. The performance of Tiffany's stock is likely to be strongly influenced by the economy. Monthly data for Tiffany's risk-adjusted return and the risk-adjusted market return are collected for a five-year period (n = 60). The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.  When testing whether the beta coefficient is significantly greater than one, the value of the test statistic is ________.
When testing whether the beta coefficient is significantly greater than one, the value of the test statistic is ________.
A) −1.98
B) 1.98
C) 4.33
D) 9.58
 When testing whether the beta coefficient is significantly greater than one, the value of the test statistic is ________.
When testing whether the beta coefficient is significantly greater than one, the value of the test statistic is ________.A) −1.98
B) 1.98
C) 4.33
D) 9.58

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
66
A researcher analyzes the factors that may influence amusement park attendance. She estimates the following model: Attendance = β0 + β1Price + β2Temperature + β3Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), Temperature is the average daily temperature (in °F), and Rides is the number of rides at the amusement park. A portion of the regression results is shown in the accompanying table. 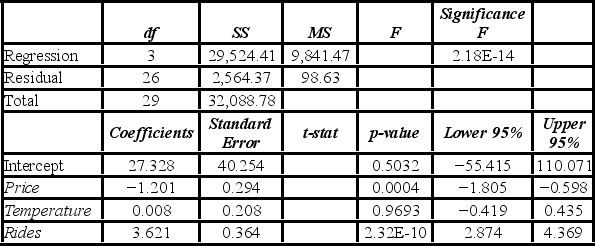 Which of the following are the hypotheses to test if the explanatory variables Temperature and Rides are jointly significant in explaining Attendance?
Which of the following are the hypotheses to test if the explanatory variables Temperature and Rides are jointly significant in explaining Attendance?
A) H0: β2 = β3 = 0; HA: At least one of the coefficients is nonzero.
B) H0: β2 = β3 = 0; HA: At least one of the coefficients is zero.
C) H0: β0 = β1 = 0; HA: At least one of the coefficients is nonzero.
D) H0: β0 = β1 = 0; HA: At least one of the coefficients is zero.
 Which of the following are the hypotheses to test if the explanatory variables Temperature and Rides are jointly significant in explaining Attendance?
Which of the following are the hypotheses to test if the explanatory variables Temperature and Rides are jointly significant in explaining Attendance?A) H0: β2 = β3 = 0; HA: At least one of the coefficients is nonzero.
B) H0: β2 = β3 = 0; HA: At least one of the coefficients is zero.
C) H0: β0 = β1 = 0; HA: At least one of the coefficients is nonzero.
D) H0: β0 = β1 = 0; HA: At least one of the coefficients is zero.

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
67
Tiffany & Co. has been the world's premier jeweler since 1837. The performance of Tiffany's stock is likely to be strongly influenced by the economy. Monthly data for Tiffany's risk-adjusted return and the risk-adjusted market return are collected for a five-year period  . The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.
. The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.  When testing whether the beta coefficient is significantly greater than one, the relevant critical value at the 5% significance level is t0.05,58 = 1.672. The conclusion to the test is to ________.
When testing whether the beta coefficient is significantly greater than one, the relevant critical value at the 5% significance level is t0.05,58 = 1.672. The conclusion to the test is to ________.
A) reject H0; we can conclude that the return on Tiffany stock is riskier than the return on the market
B) not reject H0; we can conclude that the return on Tiffany stock is riskier than the return on the market
C) reject H0; we cannot conclude that the return on Tiffany stock is riskier than the return on the market
D) not reject H0; we cannot conclude that the return on Tiffany stock is riskier than the return on the market
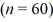 . The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.
. The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.  When testing whether the beta coefficient is significantly greater than one, the relevant critical value at the 5% significance level is t0.05,58 = 1.672. The conclusion to the test is to ________.
When testing whether the beta coefficient is significantly greater than one, the relevant critical value at the 5% significance level is t0.05,58 = 1.672. The conclusion to the test is to ________.A) reject H0; we can conclude that the return on Tiffany stock is riskier than the return on the market
B) not reject H0; we can conclude that the return on Tiffany stock is riskier than the return on the market
C) reject H0; we cannot conclude that the return on Tiffany stock is riskier than the return on the market
D) not reject H0; we cannot conclude that the return on Tiffany stock is riskier than the return on the market

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
68
A manager at a local bank analyzed the relationship between monthly salary (y, in $) and length of service (x, measured in months) for 30 employees. She estimates the following model: Salary = β0 + β1Service + ε. The following table summarizes a portion of the regression results.  Which of the following hypotheses will determine whether the intercept differs from zero?
Which of the following hypotheses will determine whether the intercept differs from zero?
A) H0: β0 = 0; HA: β0 ≠ 0
B) H0: β1 = 0; HA: β1 ≠ 0
C) H0: b0 = 0; HA: b0 ≠ 0
D) H0: b1 = 0; HA: b1 ≠ 0
 Which of the following hypotheses will determine whether the intercept differs from zero?
Which of the following hypotheses will determine whether the intercept differs from zero?A) H0: β0 = 0; HA: β0 ≠ 0
B) H0: β1 = 0; HA: β1 ≠ 0
C) H0: b0 = 0; HA: b0 ≠ 0
D) H0: b1 = 0; HA: b1 ≠ 0

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
69
A researcher analyzes the factors that may influence amusement park attendance and estimates the following model: Attendance = β0 + β1Price + β2Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), and Rides is the number of rides at the amusement park. The researcher would like to construct interval estimates for Attendance when Price and Rides equal $85 and 30, respectively. The researcher estimates a modified model where Attendance is the response variable and the explanatory variables are now defined as Price* = Price - 85 and Rides* = Rides - 30. A portion of the regression results is shown in the accompanying table.  According to the modified model, which of the following is the predicted value for Attendance when Price and Rides equal $85 and 30, respectively?
According to the modified model, which of the following is the predicted value for Attendance when Price and Rides equal $85 and 30, respectively?
A) 25,670
B) 34,410
C) 40,910
D) 55,600
 According to the modified model, which of the following is the predicted value for Attendance when Price and Rides equal $85 and 30, respectively?
According to the modified model, which of the following is the predicted value for Attendance when Price and Rides equal $85 and 30, respectively?A) 25,670
B) 34,410
C) 40,910
D) 55,600

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
70
A researcher analyzes the factors that may influence amusement park attendance. She estimates the following model: Attendance = β0 + β1Price + β2Temperature + β3Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), Temperature is the average daily temperature (in °F), and Rides is the number of rides at the amusement park. A portion of the regression results is shown in the accompanying table. 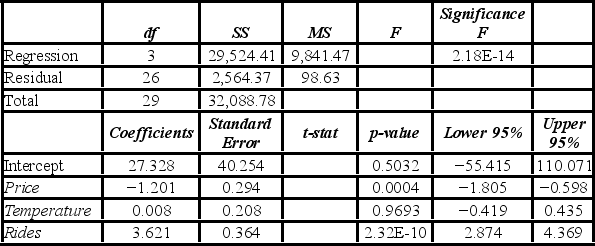 Which of the following is the value of the test statistic for testing the joint significance of the linear regression model?
Which of the following is the value of the test statistic for testing the joint significance of the linear regression model?
A) −4.09
B) 0.04
C) 9.95
D) 99.78
 Which of the following is the value of the test statistic for testing the joint significance of the linear regression model?
Which of the following is the value of the test statistic for testing the joint significance of the linear regression model?A) −4.09
B) 0.04
C) 9.95
D) 99.78

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
71
A researcher analyzes the factors that may influence amusement park attendance and estimates the following model: Attendance = β0 + β1Price + β2Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), and Rides is the number of rides at the amusement park. The researcher would like to construct interval estimates for Attendance when Price and Rides equal $85 and 30, respectively. The researcher estimates a modified model where Attendance is the response variable and the explanatory variables are now defined as
Price* = Price - 85 and Rides* = Rides - 30. A portion of the regression results is shown in the accompanying table.![<strong>A researcher analyzes the factors that may influence amusement park attendance and estimates the following model: Attendance = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), and Rides is the number of rides at the amusement park. The researcher would like to construct interval estimates for Attendance when Price and Rides equal $85 and 30, respectively. The researcher estimates a modified model where Attendance is the response variable and the explanatory variables are now defined as Price* = Price - 85 and Rides* = Rides - 30. A portion of the regression results is shown in the accompanying table. According to the modified model, which of the following is a 95% confidence interval for expected Attendance when Price and Rides equal $85 and 30, respectively? (Note that t<sub>0,025,27</sub> = 2.052.)</strong> A) [12,740, 56,780] B) [16,330, 53,450] C) [26,080, 42,740] D) [28,900, 41,500]](https://storage.examlex.com/TB6618/11ea8309_a96c_b76a_b223_c9975616fe66_TB6618_00.jpg) According to the modified model, which of the following is a 95% confidence interval for expected Attendance when Price and Rides equal $85 and 30, respectively? (Note that t0,025,27 = 2.052.)
According to the modified model, which of the following is a 95% confidence interval for expected Attendance when Price and Rides equal $85 and 30, respectively? (Note that t0,025,27 = 2.052.)
A) [12,740, 56,780]
B) [16,330, 53,450]
C) [26,080, 42,740]
D) [28,900, 41,500]
Price* = Price - 85 and Rides* = Rides - 30. A portion of the regression results is shown in the accompanying table.
![<strong>A researcher analyzes the factors that may influence amusement park attendance and estimates the following model: Attendance = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), and Rides is the number of rides at the amusement park. The researcher would like to construct interval estimates for Attendance when Price and Rides equal $85 and 30, respectively. The researcher estimates a modified model where Attendance is the response variable and the explanatory variables are now defined as Price* = Price - 85 and Rides* = Rides - 30. A portion of the regression results is shown in the accompanying table. According to the modified model, which of the following is a 95% confidence interval for expected Attendance when Price and Rides equal $85 and 30, respectively? (Note that t<sub>0,025,27</sub> = 2.052.)</strong> A) [12,740, 56,780] B) [16,330, 53,450] C) [26,080, 42,740] D) [28,900, 41,500]](https://storage.examlex.com/TB6618/11ea8309_a96c_b76a_b223_c9975616fe66_TB6618_00.jpg) According to the modified model, which of the following is a 95% confidence interval for expected Attendance when Price and Rides equal $85 and 30, respectively? (Note that t0,025,27 = 2.052.)
According to the modified model, which of the following is a 95% confidence interval for expected Attendance when Price and Rides equal $85 and 30, respectively? (Note that t0,025,27 = 2.052.)A) [12,740, 56,780]
B) [16,330, 53,450]
C) [26,080, 42,740]
D) [28,900, 41,500]

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
72
Tiffany & Co. has been the world's premier jeweler since 1837. The performance of Tiffany's stock is likely to be strongly influenced by the economy. Monthly data for Tiffany's risk-adjusted return and the risk-adjusted market return are collected for a five-year period 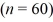 . The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.
. The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.  When testing whether there are abnormal returns, or whether the alpha coefficient is significantly different from zero, the value of the test statistic is ________.
When testing whether there are abnormal returns, or whether the alpha coefficient is significantly different from zero, the value of the test statistic is ________.
A) −1.98
B) 1.98
C) 4.33
D) 9.58
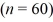 . The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.
. The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.  When testing whether there are abnormal returns, or whether the alpha coefficient is significantly different from zero, the value of the test statistic is ________.
When testing whether there are abnormal returns, or whether the alpha coefficient is significantly different from zero, the value of the test statistic is ________.A) −1.98
B) 1.98
C) 4.33
D) 9.58

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
73
Tiffany & Co. has been the world's premier jeweler since 1837. The performance of Tiffany's stock is likely to be strongly influenced by the economy. Monthly data for Tiffany's risk-adjusted return and the risk-adjusted market return are collected for a five-year period  . The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.
. The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.  When testing whether there are abnormal returns, or whether the alpha coefficient is significantly different from zero, the value of the test statistic is ________.
When testing whether there are abnormal returns, or whether the alpha coefficient is significantly different from zero, the value of the test statistic is ________.
A) H0: α = 0; HA: α ≠ 0
B) H0: β = 0; HA: β ≠ 0
C) H0: α ≤ 1; HA: α > 1
D) H0: β ≤ 1; HA: β > 1
 . The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.
. The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.  When testing whether there are abnormal returns, or whether the alpha coefficient is significantly different from zero, the value of the test statistic is ________.
When testing whether there are abnormal returns, or whether the alpha coefficient is significantly different from zero, the value of the test statistic is ________.A) H0: α = 0; HA: α ≠ 0
B) H0: β = 0; HA: β ≠ 0
C) H0: α ≤ 1; HA: α > 1
D) H0: β ≤ 1; HA: β > 1

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
74
A researcher analyzes the factors that may influence amusement park attendance. She estimates the following model: Attendance = β0 + β1Price + β2Temperature + β3Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), Temperature is the average daily temperature (in °F), and Rides is the number of rides at the amusement park. A portion of the regression results is shown in the accompanying table. 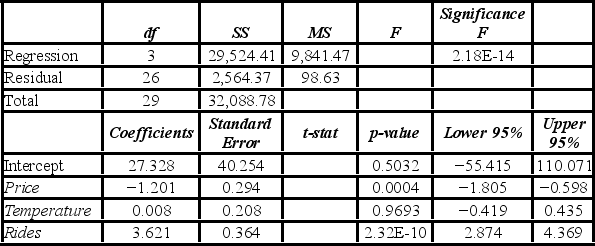 When testing whether the explanatory variables are jointly significant at the 5% significance level, the researcher ________.
When testing whether the explanatory variables are jointly significant at the 5% significance level, the researcher ________.
A) rejects H0, and concludes that the explanatory variables are jointly significant
B) does not reject H0, and concludes that the explanatory variables are jointly significant
C) rejects H0, and cannot conclude that the explanatory variables are jointly significant
D) does not reject H0, and cannot conclude that the explanatory variables are jointly significant
 When testing whether the explanatory variables are jointly significant at the 5% significance level, the researcher ________.
When testing whether the explanatory variables are jointly significant at the 5% significance level, the researcher ________.A) rejects H0, and concludes that the explanatory variables are jointly significant
B) does not reject H0, and concludes that the explanatory variables are jointly significant
C) rejects H0, and cannot conclude that the explanatory variables are jointly significant
D) does not reject H0, and cannot conclude that the explanatory variables are jointly significant

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
75
A researcher analyzes the factors that may influence amusement park attendance. She estimates the following model: Attendance = β0 + β1Price + β2Temperature + β3Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), Temperature is the average daily temperature (in °F), and Rides is the number of rides at the amusement park. A portion of the regression results is shown in the accompanying table. 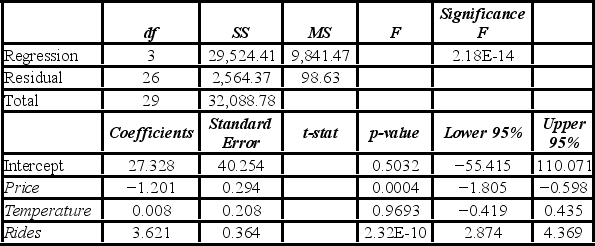 When testing whether the explanatory variables Temperature and Rides are jointly significant, the error sum of squares for the restricted model is SSER = 12,343.78. Which of the following is the value of the test statistic when conducting this test?
When testing whether the explanatory variables Temperature and Rides are jointly significant, the error sum of squares for the restricted model is SSER = 12,343.78. Which of the following is the value of the test statistic when conducting this test?
A) −4.09
B) 25.33
C) 49.58
D) 99.78
 When testing whether the explanatory variables Temperature and Rides are jointly significant, the error sum of squares for the restricted model is SSER = 12,343.78. Which of the following is the value of the test statistic when conducting this test?
When testing whether the explanatory variables Temperature and Rides are jointly significant, the error sum of squares for the restricted model is SSER = 12,343.78. Which of the following is the value of the test statistic when conducting this test?A) −4.09
B) 25.33
C) 49.58
D) 99.78

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
76
The accompanying table shows the regression results when estimating y = β0 + β1x1 + β2x2 + β3x3 + ε. 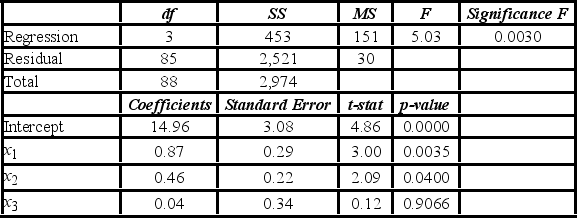 When testing whether the explanatory variables are jointly significant at the 5% significance level, the conclusion is to ________.
When testing whether the explanatory variables are jointly significant at the 5% significance level, the conclusion is to ________.
A) reject H0, and conclude that the explanatory variables are jointly significant
B) not reject H0, and conclude that the explanatory variables are jointly significant
C) reject H0, and cannot conclude that the explanatory variables are jointly significant
D) not reject H0, and cannot conclude that the explanatory variables are jointly significant
 When testing whether the explanatory variables are jointly significant at the 5% significance level, the conclusion is to ________.
When testing whether the explanatory variables are jointly significant at the 5% significance level, the conclusion is to ________.A) reject H0, and conclude that the explanatory variables are jointly significant
B) not reject H0, and conclude that the explanatory variables are jointly significant
C) reject H0, and cannot conclude that the explanatory variables are jointly significant
D) not reject H0, and cannot conclude that the explanatory variables are jointly significant

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
77
The accompanying table shows the regression results when estimating y = β0 + β1x1 + β2x2 + β3x3 + ε. 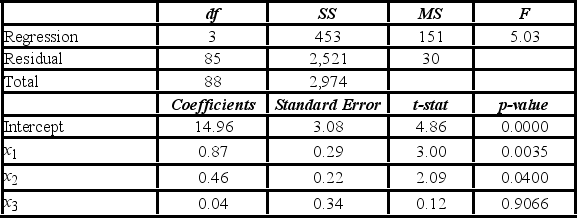 When testing whether or not x1 and x2 have the same influence on y, the null hypothesis is ________.
When testing whether or not x1 and x2 have the same influence on y, the null hypothesis is ________.
A) H0: β1 = β2
B) H0: β1 ≠ β2
C) H0: β1 + β2 = β3
D) H0: β1 + β2 = 0
 When testing whether or not x1 and x2 have the same influence on y, the null hypothesis is ________.
When testing whether or not x1 and x2 have the same influence on y, the null hypothesis is ________.A) H0: β1 = β2
B) H0: β1 ≠ β2
C) H0: β1 + β2 = β3
D) H0: β1 + β2 = 0

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
78
A researcher analyzes the factors that may influence amusement park attendance. She estimates the following model: Attendance = β0 + β1Price + β2Temperature + β3Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), Temperature is the average daily temperature (in °F), and Rides is the number of rides at the amusement park. A portion of the regression results is shown in the accompanying table. 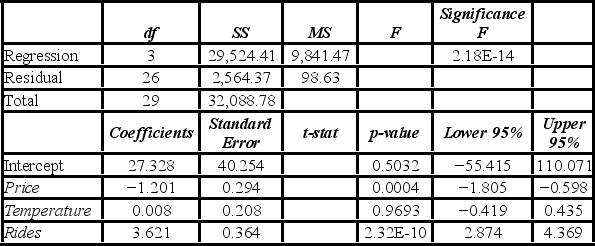 When testing whether Rides is significant at the 1% significance level, she ________.
When testing whether Rides is significant at the 1% significance level, she ________.
A) rejects H0: β3 = 0, and concludes that Rides is significant
B) does not reject H0: β3 = 0, and concludes that Rides is significant
C) rejects H0: β3 = 0, and cannot conclude that Rides is significant
D) does not reject H0: β3 = 0, and cannot conclude that Rides is significant
 When testing whether Rides is significant at the 1% significance level, she ________.
When testing whether Rides is significant at the 1% significance level, she ________.A) rejects H0: β3 = 0, and concludes that Rides is significant
B) does not reject H0: β3 = 0, and concludes that Rides is significant
C) rejects H0: β3 = 0, and cannot conclude that Rides is significant
D) does not reject H0: β3 = 0, and cannot conclude that Rides is significant

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
79
A researcher analyzes the factors that may influence amusement park attendance and estimates the following model: Attendance = β0 + β1Price + β2Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), and Rides is the number of rides at the amusement park. The researcher would like to construct interval estimates for Attendance when Price and Rides equal $85 and 30, respectively. The researcher estimates a modified model where Attendance is the response variable and the explanatory variables are now defined as Price* = Price - 85 and Rides* = Rides - 30. A portion of the regression results is shown in the accompanying table. ![<strong>A researcher analyzes the factors that may influence amusement park attendance and estimates the following model: Attendance = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), and Rides is the number of rides at the amusement park. The researcher would like to construct interval estimates for Attendance when Price and Rides equal $85 and 30, respectively. The researcher estimates a modified model where Attendance is the response variable and the explanatory variables are now defined as Price* = Price - 85 and Rides* = Rides - 30. A portion of the regression results is shown in the accompanying table. According to the modified model, which of the following is a 95% prediction interval for Attendance when Price and Rides equal $85 and 30, respectively? (Note that t<sub>0.025,27</sub> = 2.052.)</strong> A) [12,740, 56,080] B) [16,330, 53,450] C) [26,080, 42,740] D) [28,900, 41,500]](https://storage.examlex.com/TB6618/11ea8309_a96d_058b_b223_93d8e0650350_TB6618_00.jpg)
![<strong>A researcher analyzes the factors that may influence amusement park attendance and estimates the following model: Attendance = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), and Rides is the number of rides at the amusement park. The researcher would like to construct interval estimates for Attendance when Price and Rides equal $85 and 30, respectively. The researcher estimates a modified model where Attendance is the response variable and the explanatory variables are now defined as Price* = Price - 85 and Rides* = Rides - 30. A portion of the regression results is shown in the accompanying table. According to the modified model, which of the following is a 95% prediction interval for Attendance when Price and Rides equal $85 and 30, respectively? (Note that t<sub>0.025,27</sub> = 2.052.)</strong> A) [12,740, 56,080] B) [16,330, 53,450] C) [26,080, 42,740] D) [28,900, 41,500]](https://storage.examlex.com/TB6618/11ea8309_a96d_2c9c_b223_e943fadf84c1_TB6618_00.jpg) According to the modified model, which of the following is a 95% prediction interval for Attendance when Price and Rides equal $85 and 30, respectively? (Note that t0.025,27 = 2.052.)
According to the modified model, which of the following is a 95% prediction interval for Attendance when Price and Rides equal $85 and 30, respectively? (Note that t0.025,27 = 2.052.)
A) [12,740, 56,080]
B) [16,330, 53,450]
C) [26,080, 42,740]
D) [28,900, 41,500]
![<strong>A researcher analyzes the factors that may influence amusement park attendance and estimates the following model: Attendance = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), and Rides is the number of rides at the amusement park. The researcher would like to construct interval estimates for Attendance when Price and Rides equal $85 and 30, respectively. The researcher estimates a modified model where Attendance is the response variable and the explanatory variables are now defined as Price* = Price - 85 and Rides* = Rides - 30. A portion of the regression results is shown in the accompanying table. According to the modified model, which of the following is a 95% prediction interval for Attendance when Price and Rides equal $85 and 30, respectively? (Note that t<sub>0.025,27</sub> = 2.052.)</strong> A) [12,740, 56,080] B) [16,330, 53,450] C) [26,080, 42,740] D) [28,900, 41,500]](https://storage.examlex.com/TB6618/11ea8309_a96d_058b_b223_93d8e0650350_TB6618_00.jpg)
![<strong>A researcher analyzes the factors that may influence amusement park attendance and estimates the following model: Attendance = β<sub>0</sub> + β<sub>1</sub>Price + β<sub>2</sub>Rides + ε, where Attendance is the daily attendance (in 1,000s), Price is the gate price (in $), and Rides is the number of rides at the amusement park. The researcher would like to construct interval estimates for Attendance when Price and Rides equal $85 and 30, respectively. The researcher estimates a modified model where Attendance is the response variable and the explanatory variables are now defined as Price* = Price - 85 and Rides* = Rides - 30. A portion of the regression results is shown in the accompanying table. According to the modified model, which of the following is a 95% prediction interval for Attendance when Price and Rides equal $85 and 30, respectively? (Note that t<sub>0.025,27</sub> = 2.052.)</strong> A) [12,740, 56,080] B) [16,330, 53,450] C) [26,080, 42,740] D) [28,900, 41,500]](https://storage.examlex.com/TB6618/11ea8309_a96d_2c9c_b223_e943fadf84c1_TB6618_00.jpg) According to the modified model, which of the following is a 95% prediction interval for Attendance when Price and Rides equal $85 and 30, respectively? (Note that t0.025,27 = 2.052.)
According to the modified model, which of the following is a 95% prediction interval for Attendance when Price and Rides equal $85 and 30, respectively? (Note that t0.025,27 = 2.052.)A) [12,740, 56,080]
B) [16,330, 53,450]
C) [26,080, 42,740]
D) [28,900, 41,500]

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck
80
Tiffany & Co. has been the world's premier jeweler since 1837. The performance of Tiffany's stock is likely to be strongly influenced by the economy. Monthly data for Tiffany's risk-adjusted return and the risk-adjusted market return are collected for a five-year period  . The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.
. The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.  When testing whether there are abnormal returns, the conclusion to the test is at the 5% significance level is to ________.
When testing whether there are abnormal returns, the conclusion to the test is at the 5% significance level is to ________.
A) reject H0; we can conclude there are abnormal returns
B) not reject H0; we can conclude there are abnormal returns
C) reject H0; we cannot conclude there are abnormal returns
D) not reject H0, we cannot conclude there are abnormal returns
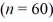 . The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.
. The accompanying table shows the regression results when estimating the Capital Asset Pricing Model (CAPM) model for Tiffany's return.  When testing whether there are abnormal returns, the conclusion to the test is at the 5% significance level is to ________.
When testing whether there are abnormal returns, the conclusion to the test is at the 5% significance level is to ________.A) reject H0; we can conclude there are abnormal returns
B) not reject H0; we can conclude there are abnormal returns
C) reject H0; we cannot conclude there are abnormal returns
D) not reject H0, we cannot conclude there are abnormal returns

Unlock Deck
Unlock for access to all 125 flashcards in this deck.
Unlock Deck
k this deck


