Deck 5: Utility and Game Theory
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/49
Play
Full screen (f)
Deck 5: Utility and Game Theory
1
A decision maker has chosen .4 as the probability for which he cannot choose between a certain loss of 10,000 and the lottery p(-25000)+ (1-p)(5000).If the utility of -25,000 is 0 and of 5000 is 1,then the utility of -10,000 is
A).5
B).6
C).4
D)4
A).5
B).6
C).4
D)4
B
2
When the decision maker prefers a guaranteed payoff value that is smaller than the expected value of the lottery,the decision maker is
A)a risk avoider.
B)a risk taker.
C)an optimist.
D)an optimizer.
A)a risk avoider.
B)a risk taker.
C)an optimist.
D)an optimizer.
A
3
The expected utility approach
A)does not require probabilities.
B)leads to the same decision as the expected value approach.
C)is most useful when excessively large or small payoffs are possible.
D)requires a decision tree.
A)does not require probabilities.
B)leads to the same decision as the expected value approach.
C)is most useful when excessively large or small payoffs are possible.
D)requires a decision tree.
C
4
The probability for which a decision maker cannot choose between a certain amount and a lottery based on that probability is
A)the indifference probability.
B)the lottery probability.
C)the uncertain probability.
D)the utility probability.
A)the indifference probability.
B)the lottery probability.
C)the uncertain probability.
D)the utility probability.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
5
For a game with an optimal pure strategy,which of the following statements is false?
A)The maximin equals the minimax.
B)The value of the game cannot be improved by either player changing strategies.
C)A saddle point exists.
D)Dominated strategies cannot exist.
A)The maximin equals the minimax.
B)The value of the game cannot be improved by either player changing strategies.
C)A saddle point exists.
D)Dominated strategies cannot exist.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
6
The decision alternative with the best expected monetary value will always be the most desirable decision.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
7
If the maximin and minimax values are not equal in a two-person zero-sum game,
A)a mixed strategy is optimal.
B)a pure strategy is optimal.
C)a dominated strategy is optimal.
D)one player should use a pure strategy and the other should use a mixed strategy.
A)a mixed strategy is optimal.
B)a pure strategy is optimal.
C)a dominated strategy is optimal.
D)one player should use a pure strategy and the other should use a mixed strategy.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
8
If the payoff from outcome A is twice the payoff from outcome B,then the ratio of these utilities will be
A)2 to 1.
B)less than 2 to 1.
C)more than 2 to 1.
D)unknown without further information.
A)2 to 1.
B)less than 2 to 1.
C)more than 2 to 1.
D)unknown without further information.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
9
When consequences are measured on a scale that reflects a decision maker's attitude toward profit,loss,and risk,payoffs are replaced by
A)utility values.
B)multicriteria measures.
C)sample information.
D)opportunity loss.
A)utility values.
B)multicriteria measures.
C)sample information.
D)opportunity loss.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
10
Values of utility
A)must be between 0 and 1.
B)must be between 0 and 10.
C)must be nonnegative.
D)must increase as the payoff improves.
A)must be between 0 and 1.
B)must be between 0 and 10.
C)must be nonnegative.
D)must increase as the payoff improves.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
11
Expected utility is a particularly useful tool when payoffs stay in a range considered reasonable by the decision maker.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
12
Which of the following statements about a dominated strategy is false?
A)A dominated strategy will never be selected by a player.
B)A dominated strategy exists if another strategy is at least as good regardless of what the opponent does.
C)A dominated strategy is superior to a mixed strategy.
D)A dominated strategy can be eliminated from the game.
A)A dominated strategy will never be selected by a player.
B)A dominated strategy exists if another strategy is at least as good regardless of what the opponent does.
C)A dominated strategy is superior to a mixed strategy.
D)A dominated strategy can be eliminated from the game.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
13
A 3 x 3 two-person zero-sum game that has no optimal pure strategy and no dominated strategies
A)can be solved using a linear programming model.
B)can be solved algebraically.
C)can be solved by identifying the minimax and maximin values.
D)cannot be solved.
A)can be solved using a linear programming model.
B)can be solved algebraically.
C)can be solved by identifying the minimax and maximin values.
D)cannot be solved.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
14
A decision maker whose utility function graphs as a straight line is
A)conservative.
B)risk neutral.
C)a risk taker.
D)a risk avoider.
A)conservative.
B)risk neutral.
C)a risk taker.
D)a risk avoider.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
15
The outcome with the highest payoff will also have the highest utility.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
16
Utility reflects the decision maker's attitude toward
A)probability and profit
B)profit,loss,and risk
C)risk and regret
D)probability and regret
A)probability and profit
B)profit,loss,and risk
C)risk and regret
D)probability and regret

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
17
For a two-person zero-sum game,which one of the following is false?
A)The gain for one player is equal to the loss for the other player.
B)A payoff of 2 for one player has a corresponding payoff of -2 for the other player.
C)The sum of the payoffs in the payoff table is zero.
D)What one player wins,the other player loses.
A)The gain for one player is equal to the loss for the other player.
B)A payoff of 2 for one player has a corresponding payoff of -2 for the other player.
C)The sum of the payoffs in the payoff table is zero.
D)What one player wins,the other player loses.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
18
To assign utilities,consider the best and worst payoffs in the entire decision situation.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
19
The purchase of insurance and lottery tickets shows that people make decisions based on
A)expected value.
B)sample information.
C)utility.
D)maximum likelihood.
A)expected value.
B)sample information.
C)utility.
D)maximum likelihood.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
20
When monetary value is not the sole measure of the true worth of the outcome to the decision maker,monetary value should be replaced by utility.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
21
For the payoff table below,the decision maker will use P(s1)= .15,P(s2)= .5,and P(s3)= .35.
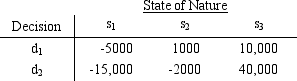
a.What alternative would be chosen according to expected value?
b.For a lottery having a payoff of 40,000 with probability p and -15,000 with probability (1-p),the decision maker expressed the following indifference probabilities.

Let U(40,000)= 10 and U(-15,000)= 0 and find the utility value for each payoff.
c.What alternative would be chosen according to expected utility?
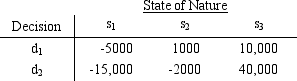
a.What alternative would be chosen according to expected value?
b.For a lottery having a payoff of 40,000 with probability p and -15,000 with probability (1-p),the decision maker expressed the following indifference probabilities.

Let U(40,000)= 10 and U(-15,000)= 0 and find the utility value for each payoff.
c.What alternative would be chosen according to expected utility?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
22
A risk neutral decision maker will have a linear utility function.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
23
The expected utility is the utility of the expected monetary value.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
24
Three decision makers have assessed utilities for the problem whose payoff table appears below.
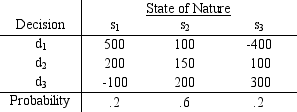
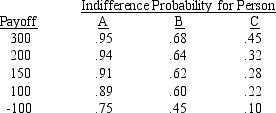
a.Plot the utility function for each decision maker.
b.Characterize each decision maker's attitude toward risk.
c.Which decision will each person prefer?


a.Plot the utility function for each decision maker.
b.Characterize each decision maker's attitude toward risk.
c.Which decision will each person prefer?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
25
Determine decision strategies based on expected value and on expected utility for this decision tree.Use the utility function
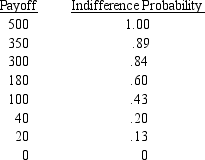
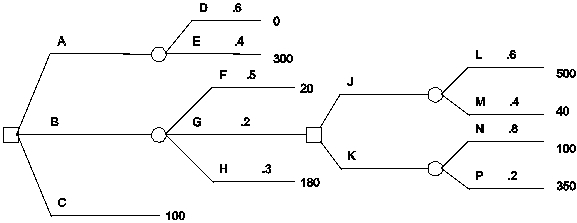 seq Figure \* Arabic1
seq Figure \* Arabic1

 seq Figure \* Arabic1
seq Figure \* Arabic1
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
26
Burger Prince Restaurant is considering the purchase of a $100,000 fire insurance policy.The fire statistics indicate that in a given year the probability of property damage in a fire is as follows:
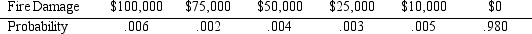
a.If Burger Prince was risk neutral,how much would they be willing to pay for fire insurance?
b.If Burger Prince has the utility values given below,approximately how much would they be willing to pay for fire insurance?
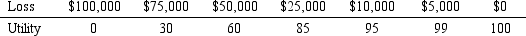
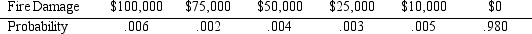
a.If Burger Prince was risk neutral,how much would they be willing to pay for fire insurance?
b.If Burger Prince has the utility values given below,approximately how much would they be willing to pay for fire insurance?
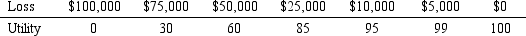

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
27
The risk premium is never negative for a conservative decision maker.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
28
The utility function for a risk avoider typically shows a diminishing marginal return for money.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
29
A decision maker has the following utility function
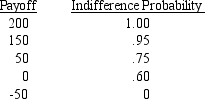 What is the risk premium for the payoff of 50?
What is the risk premium for the payoff of 50?
 What is the risk premium for the payoff of 50?
What is the risk premium for the payoff of 50?
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
30
A game has a saddle point when pure strategies are optimal for both players.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
31
The logic of game theory assumes that each player has different information.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
32
The risk neutral decision maker will have the same indications from the expected value and expected utility approaches.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
33
With a mixed strategy,the optimal solution for each player is to randomly select among two or more of the alternative strategies.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
34
A game has a pure strategy solution when both players' single-best strategies are the same.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
35
Given two decision makers,one risk neutral and the other a risk avoider,the risk avoider will always give a lower utility value for a given outcome.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
36
A game has a saddle point when the maximin payoff value equals the minimax payoff value.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
37
A risk avoider will have a concave utility function.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
38
The expected monetary value approach and the expected utility approach to decision making usually result in the same decision choice unless extreme payoffs are involved.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
39
A decision maker who is considered to be a risk taker is faced with this set of probabilities and payoffs
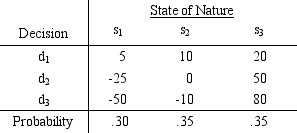 For the lottery p(80)+ (1 - p)(-50),this decision maker has assessed the following indifference probabilities
For the lottery p(80)+ (1 - p)(-50),this decision maker has assessed the following indifference probabilities
Payoff Probability
50 .60
20 .35
10 .25
5 .22
0 .20
-10 .18
-25 .10
Rank the decision alternatives on the basis of expected value and on the basis of expected utility.
 For the lottery p(80)+ (1 - p)(-50),this decision maker has assessed the following indifference probabilities
For the lottery p(80)+ (1 - p)(-50),this decision maker has assessed the following indifference probabilitiesPayoff Probability
50 .60
20 .35
10 .25
5 .22
0 .20
-10 .18
-25 .10
Rank the decision alternatives on the basis of expected value and on the basis of expected utility.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
40
Super Cola is considering the introduction of a new 8 oz.root beer.The probability that the root beer will be a success is believed to equal .6.The payoff table is as follows:
Success (s1)Failure (s2)
Produce $250,000 -$300,000
Do Not Produce -$50,000 -$20,000
Company management has determined the following utility values:
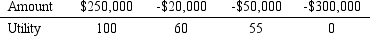
a.Is the company a risk taker,risk averse,or risk neutral?
b.What is Super Cola's optimal decision?
Success (s1)Failure (s2)
Produce $250,000 -$300,000
Do Not Produce -$50,000 -$20,000
Company management has determined the following utility values:
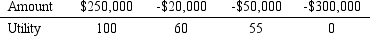
a.Is the company a risk taker,risk averse,or risk neutral?
b.What is Super Cola's optimal decision?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
41
Suppose that there are only two vehicle dealerships (A and B)in a small city.Each dealership is considering three strategies that are designed to take sales of new vehicles from the other dealership over a period of four months.The strategies,assumed to be the same for both dealerships,are:
Strategy 1: Offer a cash rebate on a new vehicle.
Strategy 2: Offer free optional equipment on a new vehicle.
Strategy 3: Offer a 0% loan on a new vehicle.
The payoff table (in number of new vehicle sales gained per week by Dealership A (or lost by Dealership B)is shown below.
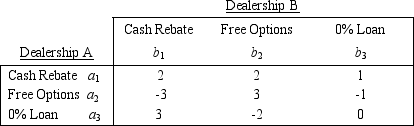 Identify the pure strategy for this two-person zero-sum game.What is the value of the game?
Identify the pure strategy for this two-person zero-sum game.What is the value of the game?
Strategy 1: Offer a cash rebate on a new vehicle.
Strategy 2: Offer free optional equipment on a new vehicle.
Strategy 3: Offer a 0% loan on a new vehicle.
The payoff table (in number of new vehicle sales gained per week by Dealership A (or lost by Dealership B)is shown below.
 Identify the pure strategy for this two-person zero-sum game.What is the value of the game?
Identify the pure strategy for this two-person zero-sum game.What is the value of the game?
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
42
Consider the following two-person zero-sum game.Assume the two players have the same three strategy options.The payoff table below shows the gains for Player A.
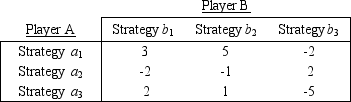 Is there an optimal pure strategy for this game? If so,what is it? If not,can the mixed-strategy probabilities be found algebraically? What is the value of the game?
Is there an optimal pure strategy for this game? If so,what is it? If not,can the mixed-strategy probabilities be found algebraically? What is the value of the game?
 Is there an optimal pure strategy for this game? If so,what is it? If not,can the mixed-strategy probabilities be found algebraically? What is the value of the game?
Is there an optimal pure strategy for this game? If so,what is it? If not,can the mixed-strategy probabilities be found algebraically? What is the value of the game?
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
43
Consider the following two-person zero-sum game.Assume the two players have the same two strategy options.The payoff table shows the gains for Player A.
 Determine the optimal strategy for each player.What is the value of the game?
Determine the optimal strategy for each player.What is the value of the game?
 Determine the optimal strategy for each player.What is the value of the game?
Determine the optimal strategy for each player.What is the value of the game?
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
44
Two banks (Franklin and Lincoln)compete for customers in the growing city of Logantown.Both banks are considering opening a branch office in one of three new neighborhoods: Hillsboro,Fremont,or Oakdale.The strategies,assumed to be the same for both banks,are:
Strategy 1: Open a branch office in the Hillsboro neighborhood.
Strategy 2: Open a branch office in the Fremont neighborhood.
Strategy 3: Open a branch office in the Oakdale neighborhood.
Values in the payoff table below indicate the gain (or loss)of customers (in thousands)for Franklin Bank based on the strategies selected by the two banks.
 Identify the neighborhood in which each bank should locate a new branch office.What is the value of the game?
Identify the neighborhood in which each bank should locate a new branch office.What is the value of the game?
Strategy 1: Open a branch office in the Hillsboro neighborhood.
Strategy 2: Open a branch office in the Fremont neighborhood.
Strategy 3: Open a branch office in the Oakdale neighborhood.
Values in the payoff table below indicate the gain (or loss)of customers (in thousands)for Franklin Bank based on the strategies selected by the two banks.
 Identify the neighborhood in which each bank should locate a new branch office.What is the value of the game?
Identify the neighborhood in which each bank should locate a new branch office.What is the value of the game?
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
45
The Dollar Department Store chain has the opportunity of acquiring either 3,5,or 10 leases from the bankrupt Granite Variety Store chain.Dollar estimates the profit potential of the leases depends on the state of the economy over the next five years.There are four possible states of the economy as modeled by Dollar Department Stores and its president estimates P(s1)= .4,P(s2)= .3,P(s3)= .1,and P(s4)= .2.The utility has also been estimated.Given the payoffs (in $1,000,000's)and utility values below,which decision should Dollar make?
Payoff Table State Of The Economy
Over The Next 5 Years
Decision s1 s2 s3 s4
 d1 -- buy 10 leases 10 5 0 -20
d1 -- buy 10 leases 10 5 0 -20
d2 -- buy 5 leases 5 0 -1 -10
d3 -- buy 3 leases 2 1 0 - 1
d4 -- do not buy 0 0 0 0
Utility Table
Payoff (in $1,000,000's)+10 +5 +2 0 -1 -10 -20
Utility +10 +5 +2 0 -1 -20 -50
Payoff Table State Of The Economy
Over The Next 5 Years
Decision s1 s2 s3 s4
 d1 -- buy 10 leases 10 5 0 -20
d1 -- buy 10 leases 10 5 0 -20d2 -- buy 5 leases 5 0 -1 -10
d3 -- buy 3 leases 2 1 0 - 1
d4 -- do not buy 0 0 0 0
Utility Table
Payoff (in $1,000,000's)+10 +5 +2 0 -1 -10 -20
Utility +10 +5 +2 0 -1 -20 -50

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
46
Consider the following two-person zero-sum game.Assume the two players have the same two strategy options.The payoff table shows the gains for Player A.
 Determine the optimal strategy for each player.What is the value of the game?
Determine the optimal strategy for each player.What is the value of the game?
 Determine the optimal strategy for each player.What is the value of the game?
Determine the optimal strategy for each player.What is the value of the game?
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
47
Chez Paul is contemplating either opening another restaurant or expanding its existing location.The payoff table for these two decisions is:
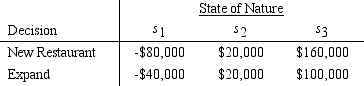 Paul has calculated the indifference probability for the lottery having a payoff of $160,000 with probability p and -$80,000 with probability (1-p)as follows:
Paul has calculated the indifference probability for the lottery having a payoff of $160,000 with probability p and -$80,000 with probability (1-p)as follows:
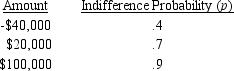
a.Is Paul a risk avoider,a risk taker,or risk neutral?
b.Suppose Paul has defined the utility of -$80,000 to be 0 and the utility of $160,000 to be 80.What would be the utility values for -$40,000,$20,000,and $100,000 based on the indifference probabilities?
c.Suppose P(s1)= .4,P(s2)= .3,and P(s3)= .3.Which decision should Paul make? Compare with the decision using the expected value approach.
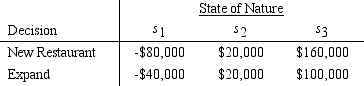 Paul has calculated the indifference probability for the lottery having a payoff of $160,000 with probability p and -$80,000 with probability (1-p)as follows:
Paul has calculated the indifference probability for the lottery having a payoff of $160,000 with probability p and -$80,000 with probability (1-p)as follows: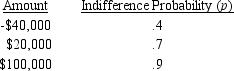
a.Is Paul a risk avoider,a risk taker,or risk neutral?
b.Suppose Paul has defined the utility of -$80,000 to be 0 and the utility of $160,000 to be 80.What would be the utility values for -$40,000,$20,000,and $100,000 based on the indifference probabilities?
c.Suppose P(s1)= .4,P(s2)= .3,and P(s3)= .3.Which decision should Paul make? Compare with the decision using the expected value approach.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
48
Consider the following two-person zero-sum game.Assume the two players have the same three strategy options.The payoff table shows the gains for Player A.
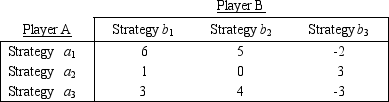 Is there an optimal pure strategy for this game? If so,what is it? If not,can the mixed-strategy probabilities be found algebraically?
Is there an optimal pure strategy for this game? If so,what is it? If not,can the mixed-strategy probabilities be found algebraically?
 Is there an optimal pure strategy for this game? If so,what is it? If not,can the mixed-strategy probabilities be found algebraically?
Is there an optimal pure strategy for this game? If so,what is it? If not,can the mixed-strategy probabilities be found algebraically?
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
49
Consider the following two-person zero-sum game.Assume the two players have the same three strategy options.The payoff table below shows the gains for Player A.
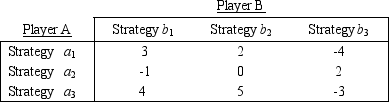 Is there an optimal pure strategy for this game? If so,what is it? If not,can the mixed-strategy probabilities be found algebraically? What is the value of the game?
Is there an optimal pure strategy for this game? If so,what is it? If not,can the mixed-strategy probabilities be found algebraically? What is the value of the game?
 Is there an optimal pure strategy for this game? If so,what is it? If not,can the mixed-strategy probabilities be found algebraically? What is the value of the game?
Is there an optimal pure strategy for this game? If so,what is it? If not,can the mixed-strategy probabilities be found algebraically? What is the value of the game?
Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck


