Deck 11: Limits and Continuity
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/241
Play
Full screen (f)
Deck 11: Limits and Continuity
1
Find: 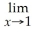
f(x)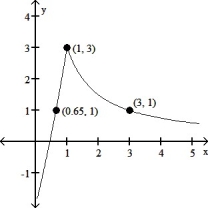
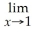
f(x)

3
2
Find: 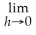
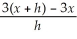
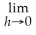
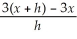
3
3
Find: lim 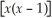
x→3
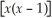
x→3
6
4
Find:

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
5
Find: 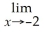
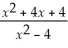
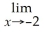
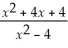

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
6
Find: 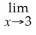
f(x)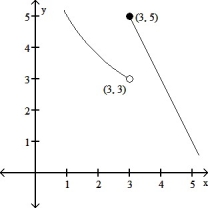
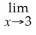
f(x)


Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
7
Find: 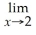
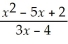
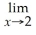
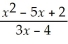

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
8
Find: lim 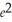
p→e
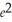
p→e

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
9
Find: lim 15
x→8
x→8

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
10
Find: 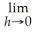
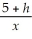
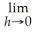
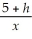

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
11
Find: 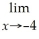
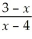
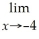
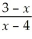

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
12
Find: 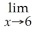
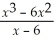
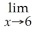
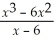

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
13
Find: 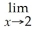
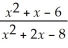
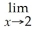
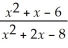

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
14
Find: 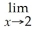
f(x)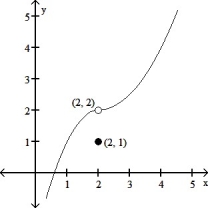
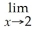
f(x)


Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
15
Find: 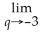
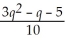
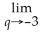
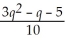

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
16
Find: 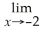
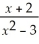
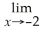
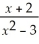

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
17
Find: 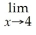
f(x)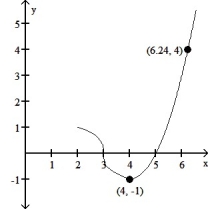
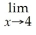
f(x)


Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
18
Find: lim ( 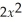
- 4x + 3)
x→3
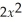
- 4x + 3)
x→3

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
19
Find: 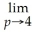
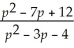
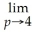
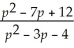

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
20
Find: 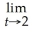
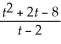
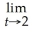
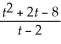

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
21
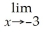
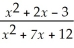
=
A) 0
B) 2
C) -4
D) 4
E) -∞

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
22
Find: 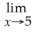
81
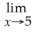
81

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
23
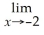 (2 +
(2 + 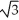
)=
A) 0
B)
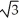
C) -2 +
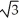
D) 2 +
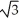
E) does not exist

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
24
If f(x)= 2x + 7,find 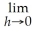
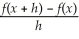
by treating x as a constant.
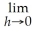
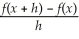
by treating x as a constant.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
25
Find: 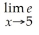
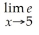

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
26
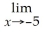
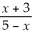
=
A) 0
B) -

C)

D) -∞
E) ∞

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
27
If f(x)= 3x - 4,find 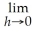
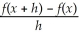
by treating x as a constant.
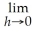
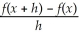
by treating x as a constant.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
28
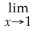
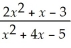
=
A) 0
B)

C)

D)
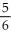
E)


Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
29
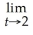
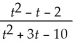
=
A)

B)

C) -1
D) -∞
E) ∞

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
30
Find 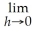
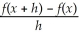
where f(x)=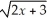
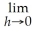
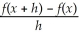
where f(x)=
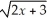

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
31
Find 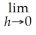
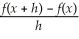
where f(x)=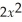
+ 3x + 5
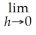
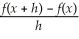
where f(x)=
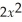
+ 3x + 5

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
32
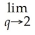
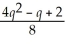
=
A)

B) 2
C) 3
D) 4
E) 5

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
33
Find: Find 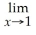
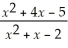
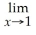
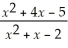

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
34
Find 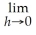
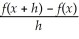
where f(x)=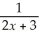
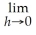
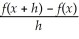
where f(x)=
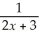

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
35
If f(x)= 6,find 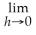
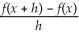
by treating x as a constant.
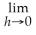
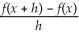
by treating x as a constant.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
36
Find: Find 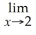
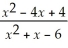
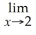
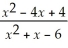

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
37
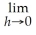
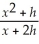
=
A) 0
B) x
C) -∞
D) ∞
E) does not exist

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
38
If f(x)= 3x - 7,then 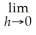
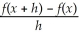
=
A) 0.
B) 3.
C) 3x.
D) -7.
E) does not exist
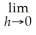
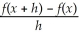
=
A) 0.
B) 3.
C) 3x.
D) -7.
E) does not exist

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
39
Find: Find 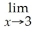
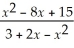
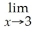
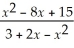

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
40
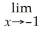
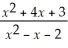
=
A) 0
B) 1
C) -4
D) -

E) ∞

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
41
The revenue function for a certain product is given by R(x)= 500x - 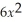
.Find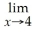
R(x).
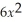
.Find
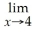
R(x).

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
42
The volume of helium in a spherical balloon (in cubic centimeters)as a function of the radius,r,in centimeters,is given by V(r)= 
π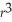
.Graph V(r)in the standard viewing rectangle,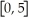
×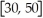
and use TRACE to estimate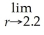
V(r).

π
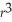
.Graph V(r)in the standard viewing rectangle,
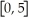
×
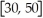
and use TRACE to estimate
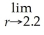
V(r).

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
43
The revenue function for a certain product is given by R(x)= 500x - 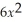
.Graph this function in the window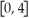
×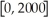
.Use TRACE to estimate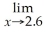
R(x).
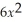
.Graph this function in the window
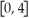
×
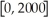
.Use TRACE to estimate
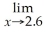
R(x).

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
44
If the profit function for a certain business is given by: P(x)= 225x - 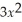
- 800,use the rule about the limit of a polynomial function to determine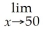
P(x).
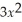
- 800,use the rule about the limit of a polynomial function to determine
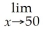
P(x).

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
45
The revenue function for a certain product is given by R(x)= 500x - 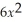
.Find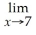
R(x).
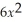
.Find
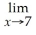
R(x).

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
46
If the profit function for a certain business is given by: P(x)= 225x - 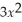
- 800,use the rule about the limit of a polynomial function to determine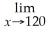
P(x).
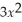
- 800,use the rule about the limit of a polynomial function to determine
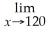
P(x).

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
47
The revenue function for a certain product is given by R(x)= 500x - 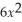
.Find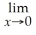
R(x).
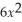
.Find
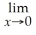
R(x).

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
48
The greatest integer function in mathematics (denoted f(x)= 
)is used every day by cashiers making change for customers.This function tells the amount of paper money for each amount of change owed.(For example,if the customer is owed $1.25 in change,he would get $1 in paper money,thus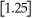
= 1).By considering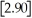
,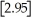
,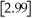
,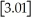
,and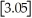
,determine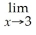

.

)is used every day by cashiers making change for customers.This function tells the amount of paper money for each amount of change owed.(For example,if the customer is owed $1.25 in change,he would get $1 in paper money,thus
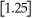
= 1).By considering
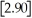
,
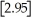
,
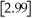
,
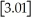
,and
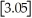
,determine
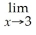

.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
49
The greatest integer function in mathematics (denoted f(x)= 
)is used every day by cashiers making change for customers.This function tells the amount of paper money for each amount of change owed.(For example,if the customer is owed $1.25 in change,he would get $1 in paper money,thus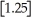
= 1).By considering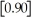
,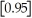
,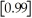
,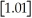
,and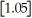
,determine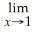

.

)is used every day by cashiers making change for customers.This function tells the amount of paper money for each amount of change owed.(For example,if the customer is owed $1.25 in change,he would get $1 in paper money,thus
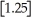
= 1).By considering
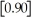
,
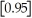
,
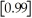
,
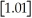
,and
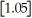
,determine
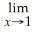

.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
50
If the profit function for a certain business is given by: P(x)= 225x - 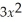
- 800,use the rule about the limit of a polynomial function to determine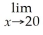
P(x).
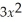
- 800,use the rule about the limit of a polynomial function to determine
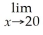
P(x).

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
51
The revenue function for a certain product is given by R(x)= 500x - 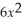
.Graph this function in the window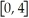
×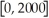
.Use TRACE to estimate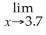
R(x).
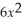
.Graph this function in the window
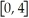
×
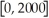
.Use TRACE to estimate
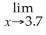
R(x).

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
52
If the profit function for a certain business is given by: P(x)= 225x - 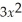
- 800,use the rule about the limit of a polynomial function to determine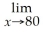
P(x).
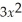
- 800,use the rule about the limit of a polynomial function to determine
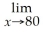
P(x).

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
53
The volume of helium in a spherical balloon (in cubic centimeters)as a function of the radius,r,in centimeters,is given by V(r)= 
π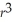
.Find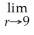
V(r).

π
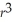
.Find
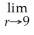
V(r).

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
54
Find: Find 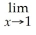
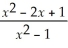
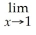
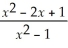

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
55
Find: Find 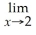
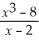
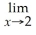
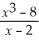

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
56
The volume of helium in a spherical balloon (in cubic centimeters)as a function of the radius,r,in centimeters,is given by V(r)= 
π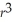
.Graph V(r)in the standard viewing rectangle,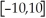
×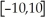
and use TRACE to estimate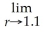
V(r).

π
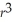
.Graph V(r)in the standard viewing rectangle,
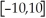
×
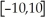
and use TRACE to estimate
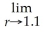
V(r).

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
57
The greatest integer function in mathematics (denoted f(x)= 
)is used every day by cashiers making change for customers.This function tells the amount of paper money for each amount of change owed.(For example,if the customer is owed $1.25 in change,he would get $1 in paper money,thus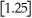
= 1).By considering
,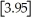
,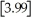
,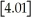
,and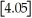
,determine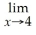

.

)is used every day by cashiers making change for customers.This function tells the amount of paper money for each amount of change owed.(For example,if the customer is owed $1.25 in change,he would get $1 in paper money,thus
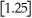
= 1).By considering

,
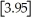
,
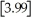
,
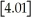
,and
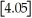
,determine
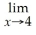

.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
58
The greatest integer function in mathematics (denoted f(x)= 
)is used every day by cashiers making change for customers.This function tells the amount of paper money for each amount of change owed.(For example,if the customer is owed $1.25 in change,he would get $1 in paper money,thus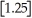
= 1).By considering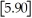
,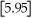
,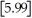
,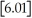
,and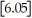
,determine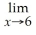

.

)is used every day by cashiers making change for customers.This function tells the amount of paper money for each amount of change owed.(For example,if the customer is owed $1.25 in change,he would get $1 in paper money,thus
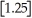
= 1).By considering
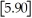
,
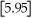
,
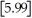
,
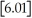
,and
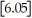
,determine
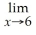

.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
59
The volume of helium in a spherical balloon (in cubic centimeters)as a function of the radius,r,in centimeters,is given by V(r)= 
π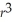
.Find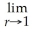
V(r).

π
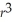
.Find
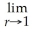
V(r).

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
60
The volume of helium in a spherical balloon (in cubic centimeters)as a function of the radius,r,in centimeters,is given by V(r)= 
π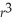
.Find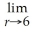
V(r).

π
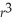
.Find
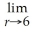
V(r).

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
61
Find: 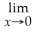

.If the limit does not exist,so state or use the symbol ∞ or -∞ if appropriate.
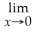

.If the limit does not exist,so state or use the symbol ∞ or -∞ if appropriate.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
62
Find: 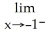
g(x)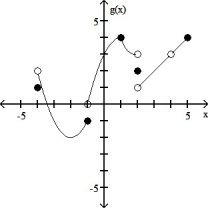
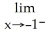
g(x)


Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
63
Find: 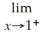
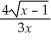
.If the limit does not exist,so state or use the symbol ∞ or -∞ if appropriate.
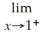
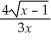
.If the limit does not exist,so state or use the symbol ∞ or -∞ if appropriate.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
64
Find: 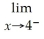
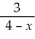
.If the limit does not exist,so state or use the symbol ∞ or -∞ if appropriate.
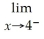
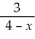
.If the limit does not exist,so state or use the symbol ∞ or -∞ if appropriate.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
65
Find: 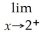
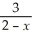
.If the limit does not exist,so state or use the symbol ∞ or -∞ if appropriate.
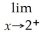
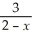
.If the limit does not exist,so state or use the symbol ∞ or -∞ if appropriate.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
66
The length of a material increases as it is heated up according to the equation 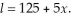
The rate at which the length is increasing is given by: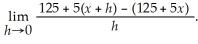
Calculate this limit.
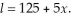
The rate at which the length is increasing is given by:
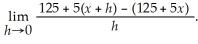
Calculate this limit.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
67
Find: 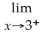
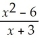
.If the limit does not exist,so state or use the symbol ∞ or -∞ if appropriate.
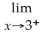
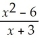
.If the limit does not exist,so state or use the symbol ∞ or -∞ if appropriate.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
68
The profit function for a certain business is given by: P(x)= 225x - 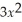
- 800.Graph this function on your graphing calculator and use the evaluation function to determine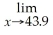
P(x)using the rule about the limit of a polynomial function.
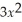
- 800.Graph this function on your graphing calculator and use the evaluation function to determine
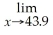
P(x)using the rule about the limit of a polynomial function.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
69
Use your calculator to complete the table,and use your results to estimate the given limit. 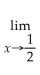
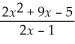
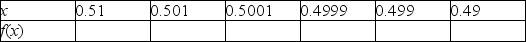
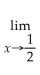
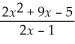
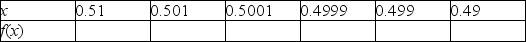

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
70
The rate of change of productivity p (in number of units produced per hour)increases with time on the job by the function p = 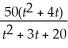
.Find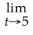
p.
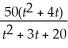
.Find
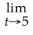
p.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
71
Find: 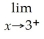
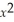
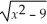
.If the limit does not exist,so state or use the symbol ∞ or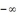
if appropriate.
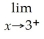
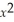
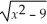
.If the limit does not exist,so state or use the symbol ∞ or
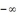
if appropriate.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
72
Find: 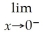

.If the limit does not exist,so state or use the symbol ∞ or -∞ if appropriate.
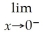

.If the limit does not exist,so state or use the symbol ∞ or -∞ if appropriate.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
73
Find: 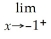
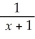
.If the limit does not exist,so state or use the symbol ∞ or -∞ if appropriate.
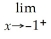
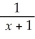
.If the limit does not exist,so state or use the symbol ∞ or -∞ if appropriate.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
74
The rate of change of productivity p (in number of units produced per hour)increases with time on the job by the function p = 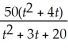
.Find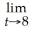
p.
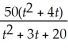
.Find
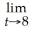
p.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
75
The rate of change of productivity p (in number of units produced per hour)increases with time on the job by the function p = 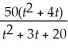
.Find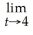
p.
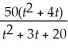
.Find
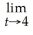
p.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
76
Find: 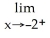
f(x)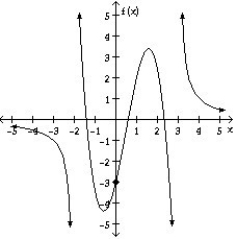
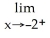
f(x)


Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
77
The length of a material increases as it is heated up according to the equation 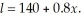
The rate at which the length is increasing is given by: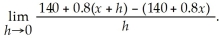
Calculate this limit.
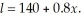
The rate at which the length is increasing is given by:
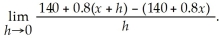
Calculate this limit.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
78
Use your calculator to complete the table,and use your results to estimate the given limit. 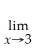
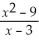

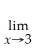
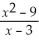


Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
79
Find: 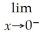
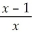
.If the limit does not exist,so state or use the symbol ∞ or -∞ if appropriate.
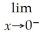
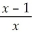
.If the limit does not exist,so state or use the symbol ∞ or -∞ if appropriate.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck
80
The length of a material increases as it is heated up according to the equation 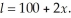
The rate at which the length is increasing is given by: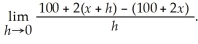
Calculate this limit.
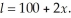
The rate at which the length is increasing is given by:
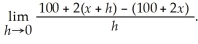
Calculate this limit.

Unlock Deck
Unlock for access to all 241 flashcards in this deck.
Unlock Deck
k this deck


