Deck 11: Extension G: Partial Derivatives
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/14
Play
Full screen (f)
Deck 11: Extension G: Partial Derivatives
1
Find and classify the relative extrema and saddle points of the function 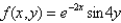 for
for 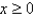 and
and 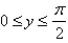
A) Relative maximum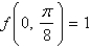
B) Saddle point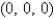
C) Relative minimum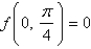
D) None
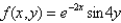 for
for 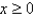 and
and 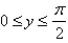
A) Relative maximum
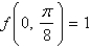
B) Saddle point
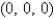
C) Relative minimum
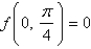
D) None
None
2
Suppose (1,1)is a critical point of a function f with continuous second derivatives. In the case of 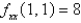 ,
, 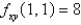 ,
, 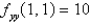 what can you say about f ?
what can you say about f ?
A) f has a saddle point at (1,1)
B) f has a local minimum at (1,1)
C) f has a local maximum at (1,1)
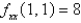 ,
, 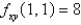 ,
, 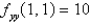 what can you say about f ?
what can you say about f ?A) f has a saddle point at (1,1)
B) f has a local minimum at (1,1)
C) f has a local maximum at (1,1)
f has a local minimum at (1,1)
3
Find the critical points of the function. 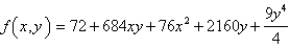
A)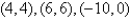
B)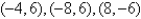
C)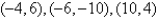
D)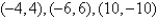
E)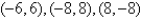
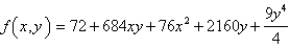
A)
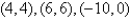
B)
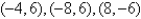
C)
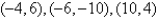
D)
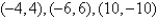
E)
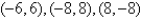
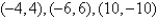
4
Find the points on the surface 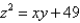 that are closest to the origin.
that are closest to the origin.
A)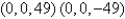
B)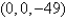
C)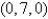
D)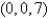
E)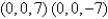
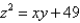 that are closest to the origin.
that are closest to the origin.A)
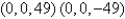
B)
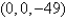
C)
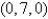
D)
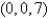
E)
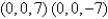

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
5
Find the absolute extrema of the function 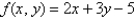 on the closed triangular region with vertices
on the closed triangular region with vertices 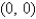 ,
, 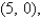 and
and 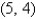
A) Absolute minimum 5, Absolute maximum 17
B) Absolute minimum 0, Absolute maximum 5
C) Absolute minimum -5, Absolute maximum 5
D) Absolute minimum -5, Absolute maximum 17
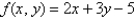 on the closed triangular region with vertices
on the closed triangular region with vertices 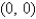 ,
, 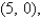 and
and 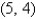
A) Absolute minimum 5, Absolute maximum 17
B) Absolute minimum 0, Absolute maximum 5
C) Absolute minimum -5, Absolute maximum 5
D) Absolute minimum -5, Absolute maximum 17

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
6
Find the dimensions of a rectangular box of maximum volume such that the sum of the lengths of its 12 edges is 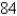
A)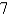 ,
, 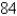 ,
, 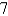
B) 4, 8, 16
C) 32,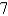 , 16
, 16
D)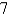 ,
, 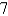 ,
, 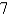
E) 32, 32, 32
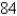
A)
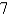 ,
, 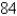 ,
, 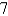
B) 4, 8, 16
C) 32,
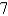 , 16
, 16D)
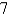 ,
, 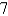 ,
, 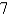
E) 32, 32, 32

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
7
Find the local maximum,and minimum value and saddle points of the function. 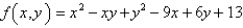
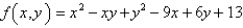

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
8
Find the absolute minimum value of the function 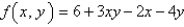 on the set D.D is the region bounded by the parabola
on the set D.D is the region bounded by the parabola 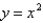 and the line
and the line 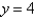
A) 0
B)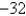
C)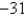
D)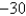
E) 30
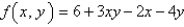 on the set D.D is the region bounded by the parabola
on the set D.D is the region bounded by the parabola 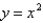 and the line
and the line 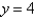
A) 0
B)
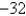
C)
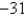
D)
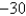
E) 30

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
9
A cardboard box without a lid is to have a volume of 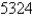 cm
cm 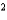 Find the dimensions that minimize the amount of cardboard used.
Find the dimensions that minimize the amount of cardboard used.
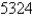 cm
cm 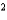 Find the dimensions that minimize the amount of cardboard used.
Find the dimensions that minimize the amount of cardboard used.
Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
10
Find three positive numbers whose sum is 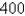 and whose product is a maximum.
and whose product is a maximum.
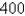 and whose product is a maximum.
and whose product is a maximum.
Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
11
Find three positive numbers whose sum is 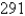 and whose product is a maximum.
and whose product is a maximum.
A)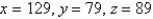
B)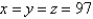
C)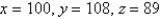
D)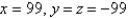
E)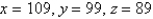
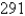 and whose product is a maximum.
and whose product is a maximum.A)
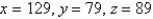
B)
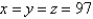
C)
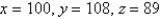
D)
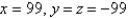
E)
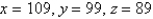

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
12
Find the shortest distance from the point 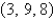 to the plane
to the plane 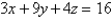
A)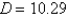
B)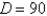
C)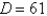
D)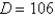
E)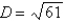
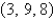 to the plane
to the plane 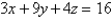
A)
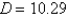
B)
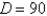
C)
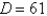
D)
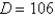
E)

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
13
Find the dimensions of the rectangular box with largest volume if the total surface area is given as 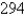
A) 21 cm, 14 cm, 1.75 cm
B) 14cm, 1.75 cm, 1.75 cm
C) 7 cm, 7 cm, 7cm
D) 294 cm, 7 cm, 7cm
E) 14 cm, 14 cm, 3.5 cm
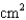
A) 21 cm, 14 cm, 1.75 cm
B) 14cm, 1.75 cm, 1.75 cm
C) 7 cm, 7 cm, 7cm
D) 294 cm, 7 cm, 7cm
E) 14 cm, 14 cm, 3.5 cm

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck
14
Find and classify the relative extrema and saddle points of the function 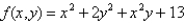
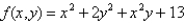

Unlock Deck
Unlock for access to all 14 flashcards in this deck.
Unlock Deck
k this deck


