Deck 13: Extension D: Vector Calculus
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/6
Play
Full screen (f)
Deck 13: Extension D: Vector Calculus
1
Use Green's Theorem to evaluate the line integral along the positively oriented closed curve C. 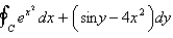 , where C is the boundary of the region bounded by the parabolas
, where C is the boundary of the region bounded by the parabolas 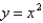 and
and 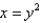
A)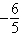 + e
+ e
B)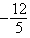 + e
+ e
C)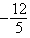
D)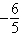
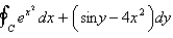 , where C is the boundary of the region bounded by the parabolas
, where C is the boundary of the region bounded by the parabolas 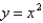 and
and 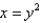
A)
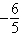 + e
+ eB)
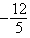 + e
+ eC)
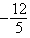
D)
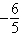
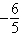
2
A particle starts at the point 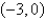 ,moves along the x-axis to (3,0)and then along the semicircle
,moves along the x-axis to (3,0)and then along the semicircle 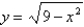 to the starting point.Use Green's Theorem to find the work done on this particle by the force field
to the starting point.Use Green's Theorem to find the work done on this particle by the force field 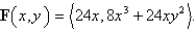
A) 0
B)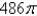
C)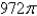
D)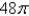
E)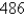
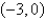 ,moves along the x-axis to (3,0)and then along the semicircle
,moves along the x-axis to (3,0)and then along the semicircle 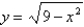 to the starting point.Use Green's Theorem to find the work done on this particle by the force field
to the starting point.Use Green's Theorem to find the work done on this particle by the force field 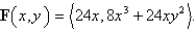
A) 0
B)
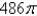
C)
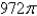
D)
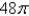
E)
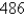
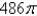
3
Use Green's Theorem to evaluate the line integral along the positively oriented closed curve C. 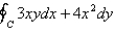 ,where C is the triangle with vertices
,where C is the triangle with vertices 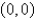 ,
, 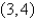 ,and
,and 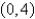
A)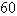
B)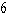
C)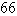
D)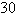
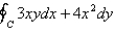 ,where C is the triangle with vertices
,where C is the triangle with vertices 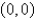 ,
, 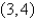 ,and
,and 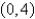
A)
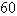
B)
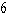
C)
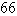
D)
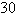
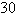
4
Let D be a region bounded by a simple closed path C in the xy.Then the coordinates of the centroid 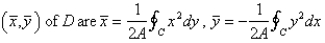 where A is the area of D. Find the centroid of the triangle with vertices (0,0),(
where A is the area of D. Find the centroid of the triangle with vertices (0,0),( 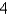 ,0)and (0,
,0)and (0, 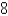 ).
).
A)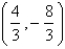
B)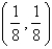
C)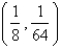
D)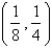
E)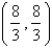
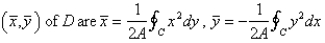 where A is the area of D. Find the centroid of the triangle with vertices (0,0),(
where A is the area of D. Find the centroid of the triangle with vertices (0,0),( 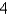 ,0)and (0,
,0)and (0, 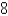 ).
).A)
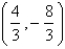
B)
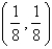
C)
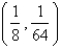
D)
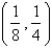
E)
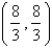

Unlock Deck
Unlock for access to all 6 flashcards in this deck.
Unlock Deck
k this deck
5
Use Green's Theorem to find the work done by the force 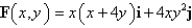 in moving a particle from the origin along the x-axis to (1,0)then along the line segment to (0,1)and then back to the origin along the y-axis.
in moving a particle from the origin along the x-axis to (1,0)then along the line segment to (0,1)and then back to the origin along the y-axis.
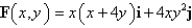 in moving a particle from the origin along the x-axis to (1,0)then along the line segment to (0,1)and then back to the origin along the y-axis.
in moving a particle from the origin along the x-axis to (1,0)then along the line segment to (0,1)and then back to the origin along the y-axis.
Unlock Deck
Unlock for access to all 6 flashcards in this deck.
Unlock Deck
k this deck
6
A plane lamina with constant density 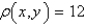 occupies a region in the xy-plane bounded by a simple closed path C.Its moments of inertia about the axes are
occupies a region in the xy-plane bounded by a simple closed path C.Its moments of inertia about the axes are 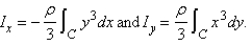 Find the moments of inertia about the axes,if C is a rectangle with vertices (0,0),(4,0), (4,5)and
Find the moments of inertia about the axes,if C is a rectangle with vertices (0,0),(4,0), (4,5)and 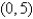
A)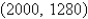
B)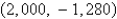
C)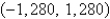
D)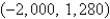
E)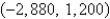
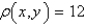 occupies a region in the xy-plane bounded by a simple closed path C.Its moments of inertia about the axes are
occupies a region in the xy-plane bounded by a simple closed path C.Its moments of inertia about the axes are 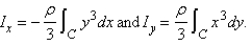 Find the moments of inertia about the axes,if C is a rectangle with vertices (0,0),(4,0), (4,5)and
Find the moments of inertia about the axes,if C is a rectangle with vertices (0,0),(4,0), (4,5)and 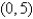
A)
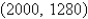
B)
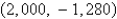
C)
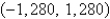
D)
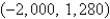
E)
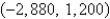

Unlock Deck
Unlock for access to all 6 flashcards in this deck.
Unlock Deck
k this deck


