Deck 13: Normal Distributions

Question 1

The weight losses for participants in a large exercise and diet study vary according to a Normal distribution with mean 14.5 pounds and standard deviation 3 pounds.
Approximately what range covers the middle 95 percent of the weight losses?

A) 11.5 to 17.5 pounds
B) 8.5 to 20.5 pounds
C) 5.5 to 21.5 pounds
D) 0 to 9 pounds

Answer 1

8.5 to 20.5 pounds

Question 2

The standard deviation of a Normal density curve is the

A) distance between the mean and the point where the curvature of the curve changes.
B) point at which the curve reaches its highest value.
C) point at which the curve would balance if made of solid material.
D) point with half the area under the curve to its left and half to its right.

Answer 2

distance between the mean and the point where the curvature of the curve changes.

Question 3

A number with 60% of the data above it is

A) the 60th percentile.
B) the 40th percentile.
C) always bigger than the mean.
D) always smaller than the mean.

Answer 3

the 40th percentile.

Question 4

The third quartile is also called the

A) 3rd percentile.
B) 25th percentile.
C) 50th percentile.
D) 75th percentile.

Question 5

The distribution of the number of dill pickle spears in a gallon container is approximately Normal with mean 110 and standard deviation 10.
Approximately what percent of the containers had between 90 and 130 spears?

A) 27 percent
B) 58 percent
C) 68 percent
D) 73 percent
E) 95 percent

Question 6

Suppose that the Blood Alcohol Content (BAC) of students who drink five beers varies from student to student according to a Normal distribution with mean 0.07 and standard deviation 0.01.
What percent of students who drink five beers have a BAC above 0.10 (the legal limit for driving in some other states)?

A) 0.15 percent
B) 0.3 percent
C) 2.5 percent
D) 16 percent
E) 32 percent

Question 7

Two measures of center are marked on the density curve below.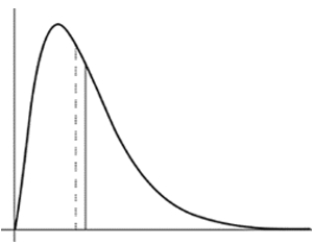

A) The median is at the solid line and the mean is at the dashed line.
B) The median is at the dashed line and the mean is at the solid line.
C) The mode is at the dashed line and the median is at the solid line.
D) The mode is at the solid line and the median is at the dashed line.

Question 8

The distribution of the number of dill pickle spears in a gallon container is approximately Normal with mean 110 and standard deviation 10.
Approximately what percent of the containers had fewer than 105 spears?

A) -50 percent
B) 50 percent
C) 30.85 percent
D) 69.15 percent
E) -30.85 percent

Question 9

A study of grades at a large university finds that the mean GPA for all undergraduates is 2.77. The distribution of grades is roughly normal. To make this description useful we must also know

A) the correlation.
B) the median.
C) the slope.
D) the standard deviation.

Question 10

The distribution of the number of dill pickle spears in a gallon container is approximately Normal with mean 110 and standard deviation 10.
If a container had to have at least 90 spears to pass quality control, approximately what percent of the containers failed? (That is, had fewer than 90 spears)?

A) 2.5 percent
B) 5 percent
C) 16 percent
D) 68 percent
E) 95 percent

Question 11

Suppose that the Blood Alcohol Content (BAC) of students who drink five beers varies from student to student according to a Normal distribution with mean 0.07 and standard deviation 0.01.
Julie is administered a BAC test and told she scored 0.085. Her standard score is:

A)100.
B)150.
C)15.
D) 1.5.
E) 0.15.

Question 12

The distribution of the number of dill pickle spears in a gallon container is approximately Normal with mean 110 and standard deviation 10.
How many dill pickle spears does a container hold if its standardized score is 0.4?

A) 4 spears
B) 14 spears
C) 104 spears
D) 114 spears
E) We don't have enough information to determine the answer to this question.

Question 13

The weight losses for participants in a large exercise and diet study vary according to a Normal distribution with mean 14.5 pounds and standard deviation 3 pounds.
Approximately what percent of the participants lose more than 20.5 pounds?

A) 2.5 percent
B) 16 percent
C) 34 percent
D) 50 percent
E) 84 percent

Question 14

The weight losses for participants in a large exercise and diet study vary according to a Normal distribution with mean 14.5 pounds and standard deviation 3 pounds.
Approximately one-half of the participants in the study lose more than:

A) 2 pounds.
B) 16.5 pounds.
C) 12.5 pounds.
D) 14.5 pounds.

Question 15

A Normal distribution always

A) is skewed to the right.
B) is skewed to the left.
C) is symmetric.
D) has a mean of 0.
E) has more than one peak.

Question 16

A student is told that her score on an exam is at the 50th percentile of the distribution of scores. This means that:

A) her score was equal to or lower than approximately 50 percent of the people who took this exam.
B) her score was equal to or higher than approximately 50 percent of the people who took this exam.
C) her score was the median score for people who took the exam.
D) if the distribution of scores was symmetric, her score would be close to the mean score for everyone who took the exam.
E) All answer choices are correct.

Question 17

The weight losses for participants in a large exercise and diet study vary according to a Normal distribution with mean 14.5 pounds and standard deviation 3 pounds.
Approximately what percent of the participants lose less than 14.5 pounds?

A) 16 percent
B) 34 percent
C) 50 percent
D) 84 percent
E) 95 percent

Question 18

Suppose that the Blood Alcohol Content (BAC) of students who drink five beers varies from student to student according to a Normal distribution with mean 0.07 and standard deviation 0.01.
What percent of students who drink five beers have a BAC above 0.08 (the legal limit for driving in most states)?

A) 0.15 percent
B) 0.3 percent
C) 2.5 percent
D) 16 percent
E) 32 percent

Question 19

The weight losses for participants in a large exercise and diet study vary according to a Normal distribution with mean 14.5 pounds and standard deviation 3 pounds.
The median amount of weight lost for the participants in this study is:

A) 11.5 pounds.
B) 14.5 pounds.
C) 17.5 pounds.
D) between 11.5 and 17.5 pounds, but can't be more specific.
E) greater than 14.5 pounds, but can't be more specific.

Question 20

Suppose that the Blood Alcohol Content (BAC) of students who drink five beers varies from student to student according to a Normal distribution with mean 0.07 and standard deviation 0.01.
The middle 95% of students who drink five beers have a BAC between

A) 0.06 and 0.08.
B) 0.05 and 0.09.
C) 0.04 and 0.10.
D) 0.03 and 0.11.

Question 21

The distribution of the number of dill pickle spears in a gallon container is approximately Normal with mean 110 and standard deviation 10.
A container with a standardized score of 0.4 is at the 65.54th percentile. What percent of the containers held more pickle spears than this container?

A) 65.54 percent
B) 40 percent
C) 34.46 percent
D) 0.4 percent
E) We can't tell from the given information.

Question 22

Scores on the American College Testing (ACT) college entrance exam follow the Normal distribution with mean 18 and standard deviation 6. Wayne's standard score on the ACT was -1.1.
Wayne's buddy Garth took the SAT. His standard score on the SAT was 0.6. This means that Garth's actual score was

A) more than 1 standard deviation below the mean SAT score.
B) less than 1 standard deviation below the mean SAT score.
C) less than 1 standard deviation above the mean SAT score.
D) more than 1 standard deviation above the mean SAT score.
E) Can't tell without knowing the standard deviation.

Question 23

Your score on the statistics final exam is at the 70th percentile of the scores for the class. Your score lies

A) below the first quartile.
B) between the first quartile and the median.
C) between the median and the third quartile.
D) above the third quartile.
E) Can't tell which quarter your score lies in.

Question 24

About what percent of the cockroaches have weights between 76 grams and 84 grams?
The weights of cockroaches follow a Normal distribution with mean 80 grams and standard deviation 2 grams. The figure below is the Normal curve for this distribution of weights.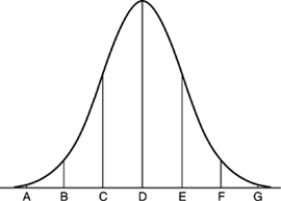

A) 99.7 percent
B) 95 percent
C) 68 percent
D) 47.5 percent
E) 34 percent

Question 25

Record the death rate from heart disease per 100,000 people in a group of developed countries. The distribution is roughly described by this Normal curve: 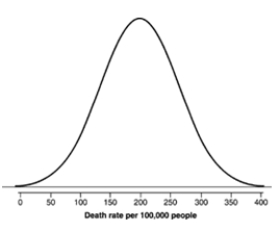From this Normal curve, we see that the mean heart disease death rate per 100,000 people is about

A) 60.
B) 120.
C) 190.
D) 250.
E) 400.

Question 26

Scores of adults aged 60 to 64 on a common IQ test are approximately Normally distributed with mean 90 and standard deviation 15.
The third quartile of the distribution of IQ scores of adults aged 60 to 64 is between

A) 90 and 105.
B) 105 and 120.
C) 90 and 75.
D) 60 and 75.

Question 27

The distribution of the number of dill pickle spears in a gallon container is approximately Normal with mean 110 and standard deviation 10.
The median number of pickle spears for this sort of container:

A) is less than 110 spears.
B) is equal to 110 spears.
C) is greater than 110 spears.
D) could be anywhere between 100 points and 120 spears.
E) is unknown-it could be either less than 110 points or greater than 110 points.

Question 28

The weights of cockroaches follow a Normal distribution with mean 80 grams and standard deviation 2 grams. The figure below is the Normal curve for this distribution of weights. 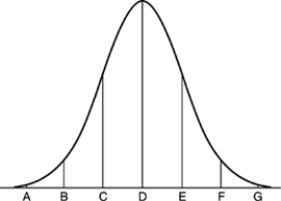At which point on the Normal curve is the median of the distribution of cockroach weights located?

A) C
B) D
C) E
D) Either point C or point E is correct, but can't tell which.
E) Can't tell from the information given.

Question 29

The weights of cockroaches follow a Normal distribution with mean 80 grams and standard deviation 2 grams. The figure below is the Normal curve for this distribution of weights. 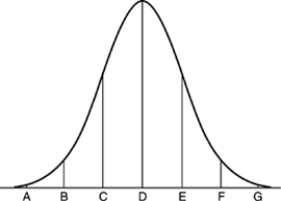Point A on this Normal curve corresponds to

A) 68 grams.
B) 68 (grams)².
C) 72 grams.
D) 74 grams.
E) 76 grams.

Question 30

Scores of adults aged 60 to 64 on a common IQ test are approximately Normally distributed with mean 90 and standard deviation 15.
What range of IQ scores contains the central 95% of the population of adults aged 60 to 64?

A) 75 to 105
B) 60 to 120
C) 30 to 150
D) 45 to 135

Question 31

Scores on the American College Testing (ACT) college entrance exam follow the Normal distribution with mean 18 and standard deviation 6. Wayne's standard score on the ACT was -1.1.
Wayne scored better than approximately

A) 1.1% of the people who took the exam.
B) 13.57% of the people who took the exam.
C) 11.40% of the people who took the exam.
D) 86.43% of the people who took the exam.

Question 32

Record the death rate from heart disease per 100,000 people in a group of developed countries. The distribution is roughly described by this Normal curve: 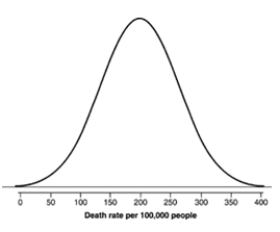From the Normal curve, we see that the standard deviation of the heart disease rate per 100,000 people is about

A) 25.
B) 65.
C) 100.
D) 200.
E) 265.

Question 33

The 34th percentile of a distribution is

A) the number with 34% of the data below it.
B) the number with 34% of the data above it.
C) the number that is 34% of the average.
D) 34% of the sample size.

Question 34

The weights of cockroaches follow a Normal distribution with mean 80 grams and standard deviation 2 grams. The figure below is the Normal curve for this distribution of weights. 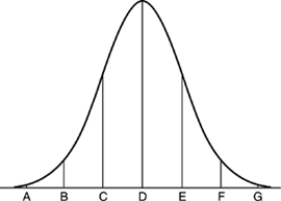About what percent of the cockroaches have weights less than 78 grams?

A) 47.5 percent
B) 34 percent
C) 32 percent
D) 16 percent
E) 2.5 percent

Question 35

If the heights of 99.7% of American men are between 5'0" and 7'0", what is your estimate of the standard deviation of the height of American men? Assume the heights of American men are approximately Normally distributed.

A) 1 inch
B) 3 inches
C) 4 inches
D) 6 inches
E) 12 inches

Question 36

Scores of adults on the Wechsler Adult Intelligence Scale (a common IQ test) follow a Normal distribution. The middle 95% of scores on this test range from 70 to 130. What is the standard deviation of the test scores?

A) 100 points
B) 20 points
C) 15 points
D) 7.5 points
E) 5 points

Question 37

The 50th percentile of a distribution is

A) the number with 50% of the data below it.
B) the number with 50% of the data above it.
C) the number with 50% of the data on either side of it.
D) All of the above

Question 38

The weights of cockroaches follow a Normal distribution with mean 80 grams and standard deviation 2 grams. The figure below is the Normal curve for this distribution of weights. 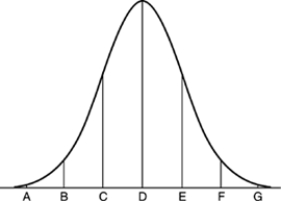Point C on this Normal curve corresponds to

A) 84 grams.
B) 82 grams.
C) 78 grams.
D) 76 grams.
E) 76 (grams)².

Question 39

Scores on the American College Testing (ACT) college entrance exam follow the Normal distribution with mean 18 and standard deviation 6. Wayne's standard score on the ACT was -1.1.
What was Wayne's actual ACT score?

A) 6.6
B) -6.6
C) 11.4
D) 24.6
E) 19.8

Question 40

Scores of adults aged 60 to 64 on a common IQ test are approximately Normally distributed with mean 90 and standard deviation 15.
Since IQ scores of adults aged 60 to 64 are Normally distributed with mean 90 and standard deviation 15, then about 40% of the scores are between

A) 60 and 120.
B) 45 and 135.
C) 85 and 90.
D) the 25th and 75th percentiles.
E) the 30th and 70th percentiles.

Question 41

Baltimore officials discovered 107 million orb-weaving spiders had infested a disused water treatment plant, according to an entomology society website. If the spiders' weights are Normally distributed with mean 11 grams and standard deviation 2 grams, approximately how many spiders in the colony weigh more than 12 grams?

A) 0.309
B) 309,000
C) 74,000,000
D) 33,000,000
E) 610,000

Question 42

What percent of the observations from a Normal distribution lie between a standard score of -1 and a standard score of 2? (Hint: sketch a Normal curve.)

A) 16%
B) 47.5%
C) 50%
D) 61%
E) 81.5%

Question 43

Scores of adults aged 60 to 64 on a common IQ test are approximately Normally distributed with mean 90 and standard deviation 15.
About what percent of the population of adults aged 60 to 64 have an IQ lower than 60?

A) 90 percent
B) 20 percent
C) 16 percent
D) 10 percent
E) 2.5 percent

Question 44

The risk of an investment is measured by the variability of the changes in its value over a fixed period, such as a year. More variation from year to year means more risk. The government's Securities and Exchange Commission wants to require mutual funds to tell investors how risky they are. A news article (New York Times, April 2, 1995) says that some people think that "the proposed risk descriptions, especially one that goes by the daunting name standard deviation" are hard to understand. Explain to a friend what the standard deviation means, using the fact that the changes in a mutual fund's value over many years have a roughly Normal distribution.

A) The standard deviation is the distance between the first and third quartiles, so it spans half the yearly changes in the fund's value.
B) The standard deviation is the largest change we ever expect to see in a year.
C) The yearly change in the fund's value will be greater than the standard deviation half the time and less than the standard deviation half the time.
D) Start with the average (mean) change in the fund's value over many years; the actual change will be within one standard deviation of that average in about 68% of all years.
E) Start with the average (mean) change in the fund's value over many years; the actual change will be within one standard deviation of that average in about 95% of all years.

Question 45

A (statistically savvy) local angler remarks that the weights of the blue gill (fish) caught from Big Bass Lake are Normally distributed. He doesn't remember the mean or the standard deviation, but he does remember that the first quartile is 2 pounds, 2 ounces and the third quartile is 3 pounds, 6 ounces. The standard deviation of blue gill weights is closest to:

A) 20 ounces.
B) 15 ounces.
C) 12 ounces.
D) 10 ounces.
E) 5 ounces.

Question 46

George has an average bowling score of 180 and bowls in a league where the average for all bowlers is 150 and the standard deviation is 20. Bill has an average bowling score of 190 and bowls in a league where the average is 160 and the standard deviation is 15. Who ranks higher in his own league, George or Bill?

A) Bill because his 190 is higher than George's 180.
B) Bill because his standard score is higher than George's.
C) George because his standard score is higher than Bill's.
D) Bill and George have the same rank in their leagues because both are 30 pins above the mean.

Question 47

Suppose that the distribution of heart rates for medium-sized dogs is Normally distributed with mean 115 beats per minute and standard deviation 18 beats per minute.
Stacy takes her medium-sized dog, Scooter, to the veterinarian for a wellness check and learns that Scooter's heart rate is 126 beats per minute. What is the approximate standard score for Scooter's heart rate?

A) -0.6
B) 0.6
C) 7
D) 11
E) 18

Question 48

Scores of adults aged 60 to 64 on a common IQ test are approximately Normally distributed with mean 90 and standard deviation 15.
Suppose we call an IQ of 90 "normal" for adults aged 60 to 64. What percent of the population have "below normal" IQs?

A) About 50%
B) Less than 50%
C) More than 50%
D) Can't tell from the information given.

Question 49

The standard score for any observation is the

A) number of standard deviations the observation is from the mean.
B) range covered by the middle half of the data.
C) distance from the mean to the point where the concavity of the density curve changes.
D) percentage of data values that fall at or below the observation.

Question 50

Suppose that the distribution of heart rates for medium-sized dogs is Normally distributed with mean 115 beats per minute and standard deviation 18 beats per minute.
Stacy takes her medium-sized dog, Scooter, to the veterinarian for a wellness check and learns that Scooter's heart rate is 126 beats per minute. Approximately what percentage of medium-sized dogs have a heart rate that is lower than Scooter's?

A) -60%.
B) 27.42%.
C) 60%.
D) 72.58%.
E) 99.4%.

Question 51

The amount of scholarships received among undergraduates at Mountain Tech are approximately Normally distributed. The mean scholarship grant is $12,000. About 95 percent of undergraduates received scholarship amounts between $7,000 and $17,000. The standard deviation of these scholarship amounts is about:

A) $5,000.
B) $10,000.
C) $12,000.
D) $20,000.
E) $2,500.

Question 52

Suppose that the distribution of heart rates for medium-sized dogs is Normally distributed with mean 115 beats per minute and standard deviation 18 beats per minute.
Stacy learns from the veterinarian that dogs with heart rates in the upper 8% may be in danger of heart failure. For medium-sized dogs, a dangerous heart rate would be one above what value?

A) 79
B) 189.8
C) 140.2
D) 151.2
E) 169

Question 53

Suppose that the distribution of heart rates for medium-sized dogs is Normally distributed with mean 115 beats per minute and standard deviation 18 beats per minute.
Approximately what percentage of medium-sized dogs have a heart rate below 115 beats per minute?

A) 16%
B) 34%
C) 50%
D) 68%
E) 95%

Question 54

In Big Bear Lake, the blue gill (fish) lengths average 8 inches and have a standard deviation of 2 inches. In Moose Jaw Lake, the blue gill lengths average 9.5 inches and have a standard deviation of 1 inch. If people are basing a successful fishing trip on the proportion of fish over 11 inches, they should head for:

A) Big Bear Lake.
B) Moose Jaw Lake.
C) either lake, because the percentages are the same.
D) It is not possible to tell from the information given.