Deck 4: Polynomial and Rational Functions Applications to Optimization
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/25
Play
Full screen (f)
Deck 4: Polynomial and Rational Functions Applications to Optimization
1
Find all fixed points of the function. 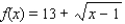
A) x = 17
B) x = 0, x = 170
C) x = 10
D) x = 17, x = 10
E) no fixed points
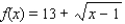
A) x = 17
B) x = 0, x = 170
C) x = 10
D) x = 17, x = 10
E) no fixed points
x = 17
2
Suppose that the revenue generated by selling x units of a certain commodity is given by 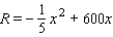 . Assume that R is in dollars. What is the maximum revenue possible in this situation?
. Assume that R is in dollars. What is the maximum revenue possible in this situation?
A) $450,000
B) $440,000
C) $430,000
D) $900,000
E) $480,000
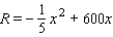 . Assume that R is in dollars. What is the maximum revenue possible in this situation?
. Assume that R is in dollars. What is the maximum revenue possible in this situation?A) $450,000
B) $440,000
C) $430,000
D) $900,000
E) $480,000
$450,000
3
Sketch the graph of the function and specify all x- and y-intercepts. y = - 3x 4 + 5
A)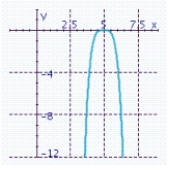 x-intercepts: 5
x-intercepts: 5
Y-intercept: - 50,625
B)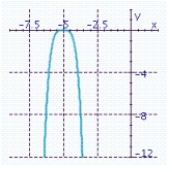 x-intercepts: -5
x-intercepts: -5
Y-intercept: - 50,625
C)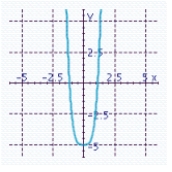 x-intercepts:
x-intercepts: 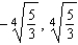
Y-intercept: - 5
D)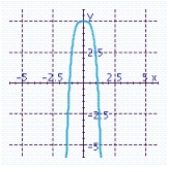 x-intercepts:
x-intercepts: 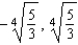
Y-intercept: 5
E)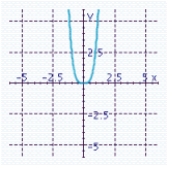 x-intercept: 0
x-intercept: 0
Y-intercept: 0
A)
 x-intercepts: 5
x-intercepts: 5Y-intercept: - 50,625
B)
 x-intercepts: -5
x-intercepts: -5Y-intercept: - 50,625
C)
 x-intercepts:
x-intercepts: 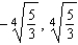
Y-intercept: - 5
D)
 x-intercepts:
x-intercepts: 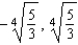
Y-intercept: 5
E)
 x-intercept: 0
x-intercept: 0Y-intercept: 0
 x-intercepts:
x-intercepts: 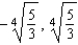
Y-intercept: 5
4
Graph the quadratic function. Specify the vertex, axis of symmetry, maximum or minimum value, and intercepts. 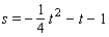
A) vertex: (- 2, 0); axis of symmetry: t = - 2; maximum value: 0; t-intercept: - 2; s-intercept: -1.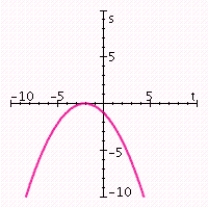
B) vertex: (- 2, 0); axis of symmetry: t = - 2; minimum value: 0; t-intercept: - 2; s-intercept: 1.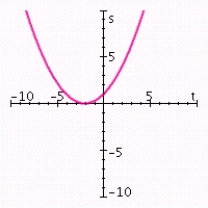
C) vertex: (2, 0); axis of symmetry: t = 2; maximum value: 0; t-intercept: 2; s-intercept: -1.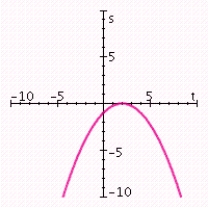
D) vertex: (0,1); axis of symmetry: t = 0; maximum value: 1; t-intercept: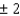 ; s-intercept: 1.
; s-intercept: 1. 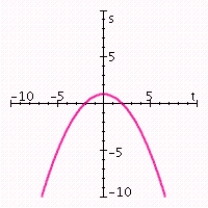
E) vertex: (0, 2);axis of symmetry: t = 0; maximum value: 2; t-intercept: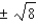 ;s-intercept: 2.
;s-intercept: 2. 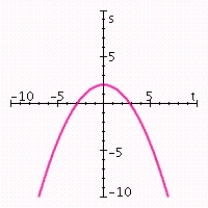
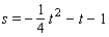
A) vertex: (- 2, 0); axis of symmetry: t = - 2; maximum value: 0; t-intercept: - 2; s-intercept: -1.

B) vertex: (- 2, 0); axis of symmetry: t = - 2; minimum value: 0; t-intercept: - 2; s-intercept: 1.

C) vertex: (2, 0); axis of symmetry: t = 2; maximum value: 0; t-intercept: 2; s-intercept: -1.

D) vertex: (0,1); axis of symmetry: t = 0; maximum value: 1; t-intercept:
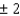 ; s-intercept: 1.
; s-intercept: 1. 
E) vertex: (0, 2);axis of symmetry: t = 0; maximum value: 2; t-intercept:
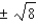 ;s-intercept: 2.
;s-intercept: 2. 

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
5
Sketch the graph of the function and specify all x- and y-intercepts. y =- ( x - 3) 3 - 1
A)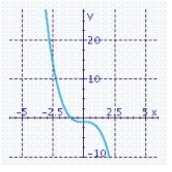 x-intercept: -1
x-intercept: -1
Y-intercept: -1
B)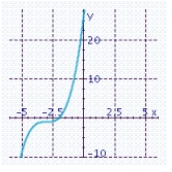 x-intercept: -2
x-intercept: -2
Y-intercept: 26
C)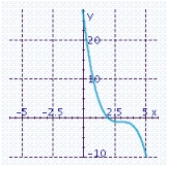 x-intercept: 2
x-intercept: 2
Y-intercept: 26
D)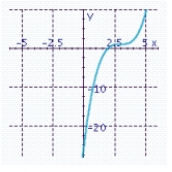 x-intercept: 2
x-intercept: 2
Y-intercept: - 26
E)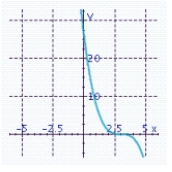 x-intercept: 3
x-intercept: 3
Y-intercept: 27
A)
 x-intercept: -1
x-intercept: -1Y-intercept: -1
B)
 x-intercept: -2
x-intercept: -2Y-intercept: 26
C)
 x-intercept: 2
x-intercept: 2Y-intercept: 26
D)
 x-intercept: 2
x-intercept: 2Y-intercept: - 26
E)
 x-intercept: 3
x-intercept: 3Y-intercept: 27

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
6
A triangle is inscribed in a semicircle of diameter 6R. Show that the smallest possible value for the area of the shaded region is 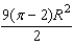 .
. 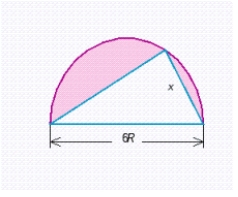 Hint: The area of the shaded region is a minimum when the area of the triangle is a maximum. Find the value of x that maximizes the square of the area of the triangle. This will be the same x that maximizes the area of the triangle.
Hint: The area of the shaded region is a minimum when the area of the triangle is a maximum. Find the value of x that maximizes the square of the area of the triangle. This will be the same x that maximizes the area of the triangle.
A) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The area of the triangle is equal to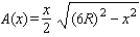 .
.
The square of the area of the triangle is equal to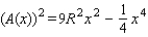 , and the substitution
, and the substitution 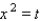 will transform this expression into the quadratic function
will transform this expression into the quadratic function 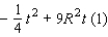
Since we want to find the maximum value of t, we will substitute the value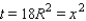 into the equation. Solving for t gives us the following minimum area of the shaded region:
into the equation. Solving for t gives us the following minimum area of the shaded region: 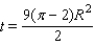 .
.
B) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The area of the triangle is equal to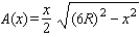 .
.
The square of the area of the triangle is equal to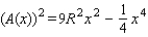 The substitution
The substitution 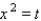 will transform this expression into the quadratic function
will transform this expression into the quadratic function 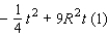
Since the graph of equation (1) will be a parabola opening downward, the input t that yields a maximum value for this function is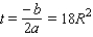
Substituting the value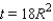 into the equation
into the equation 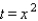 gives us
gives us 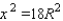 and consequently
and consequently 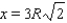 (The negative root can be rejected since the side of a triangle can't be negative). With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to
(The negative root can be rejected since the side of a triangle can't be negative). With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to 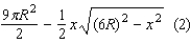
Substituting the value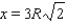 in the equation (2) gives us that the minimum value of the shaded region is equal to
in the equation (2) gives us that the minimum value of the shaded region is equal to 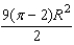 .
.
C) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The square of the area of the triangle is equal to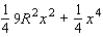 .
.
The substitution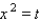 will transform this into the quadratic function
will transform this into the quadratic function 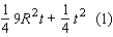
Since the graph of equation (1) will be a parabola opening downward, the input t that yields a maximum value for this function is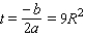
Substituting the value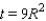 into the equation
into the equation 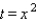 gives us
gives us 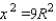 and consequently
and consequently 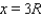 . With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to
. With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to 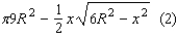
Substituting the value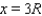 into the equation (2), we find that the minimum value of the shaded region is equal to
into the equation (2), we find that the minimum value of the shaded region is equal to 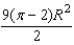 .
.
D) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle.
The square of the area of the triangle is equal to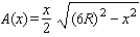 , which is a quadratic function. The graph of this function will be a parabola opening downward, so we can write the maximum value of this function as:
, which is a quadratic function. The graph of this function will be a parabola opening downward, so we can write the maximum value of this function as: 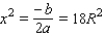
We can then write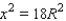 as
as 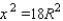 and calculate the minimum area of the shaded region. Substituting this value into the area equation, we find its minimum area:
and calculate the minimum area of the shaded region. Substituting this value into the area equation, we find its minimum area: 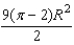 .
.
E) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The square of the area of the triangle is equal to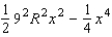 .
.
The substitution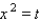 will transform this into the quadratic function
will transform this into the quadratic function 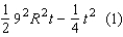
Since the graph of equation (1) will be a parabola opening downward, the input t that yields a maximum value for this function is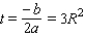
Substituting the value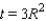 into the equation
into the equation 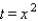 gives us
gives us 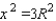 and consequently
and consequently 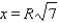 . With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to
. With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to 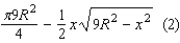
Substituting the value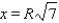 into the equation (2), we find that the minimum value of the shaded region is equal to
into the equation (2), we find that the minimum value of the shaded region is equal to 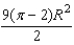 .
.
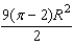 .
.  Hint: The area of the shaded region is a minimum when the area of the triangle is a maximum. Find the value of x that maximizes the square of the area of the triangle. This will be the same x that maximizes the area of the triangle.
Hint: The area of the shaded region is a minimum when the area of the triangle is a maximum. Find the value of x that maximizes the square of the area of the triangle. This will be the same x that maximizes the area of the triangle.A) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The area of the triangle is equal to
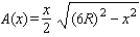 .
.The square of the area of the triangle is equal to
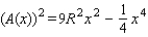 , and the substitution
, and the substitution 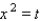 will transform this expression into the quadratic function
will transform this expression into the quadratic function 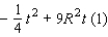
Since we want to find the maximum value of t, we will substitute the value
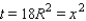 into the equation. Solving for t gives us the following minimum area of the shaded region:
into the equation. Solving for t gives us the following minimum area of the shaded region: 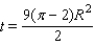 .
.B) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The area of the triangle is equal to
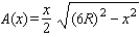 .
.The square of the area of the triangle is equal to
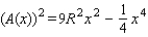 The substitution
The substitution 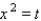 will transform this expression into the quadratic function
will transform this expression into the quadratic function 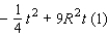
Since the graph of equation (1) will be a parabola opening downward, the input t that yields a maximum value for this function is
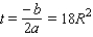
Substituting the value
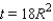 into the equation
into the equation 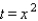 gives us
gives us 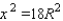 and consequently
and consequently 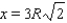 (The negative root can be rejected since the side of a triangle can't be negative). With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to
(The negative root can be rejected since the side of a triangle can't be negative). With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to 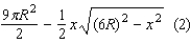
Substituting the value
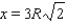 in the equation (2) gives us that the minimum value of the shaded region is equal to
in the equation (2) gives us that the minimum value of the shaded region is equal to 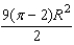 .
.C) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The square of the area of the triangle is equal to
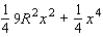 .
.The substitution
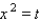 will transform this into the quadratic function
will transform this into the quadratic function 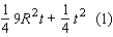
Since the graph of equation (1) will be a parabola opening downward, the input t that yields a maximum value for this function is
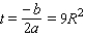
Substituting the value
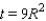 into the equation
into the equation 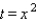 gives us
gives us 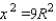 and consequently
and consequently 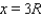 . With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to
. With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to 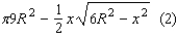
Substituting the value
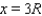 into the equation (2), we find that the minimum value of the shaded region is equal to
into the equation (2), we find that the minimum value of the shaded region is equal to 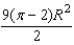 .
.D) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle.
The square of the area of the triangle is equal to
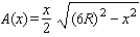 , which is a quadratic function. The graph of this function will be a parabola opening downward, so we can write the maximum value of this function as:
, which is a quadratic function. The graph of this function will be a parabola opening downward, so we can write the maximum value of this function as: 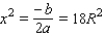
We can then write
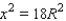 as
as 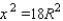 and calculate the minimum area of the shaded region. Substituting this value into the area equation, we find its minimum area:
and calculate the minimum area of the shaded region. Substituting this value into the area equation, we find its minimum area: 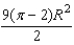 .
.E) The hint tells us that the area of the region is a minimum when the area of the triangle is a maximum. We first find the value of x that maximizes the square of the area of the triangle. The square of the area of the triangle is equal to
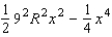 .
.The substitution
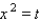 will transform this into the quadratic function
will transform this into the quadratic function 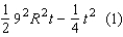
Since the graph of equation (1) will be a parabola opening downward, the input t that yields a maximum value for this function is
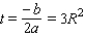
Substituting the value
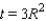 into the equation
into the equation 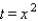 gives us
gives us 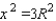 and consequently
and consequently 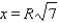 . With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to
. With this value of x, we can calculate the minimum area of the shaded region. The minimum area of the shaded region is equal to 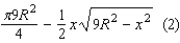
Substituting the value
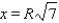 into the equation (2), we find that the minimum value of the shaded region is equal to
into the equation (2), we find that the minimum value of the shaded region is equal to 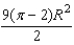 .
.
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
7
Plot the following points: (6, 2), (7, 5), (8, 8), (9, 9). In your scatter diagram, sketch a line that best seems to fit the data. Estimate the slope and the y-intercept of the line.
A) Estimated slope: 2; Estimated y-intercept: -12.5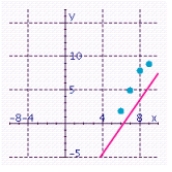
B) Estimated slope: 2.5; Estimated y-intercept: -13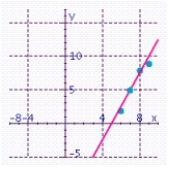
C) Estimated slope: 2.9; Estimated y-intercept: -15.3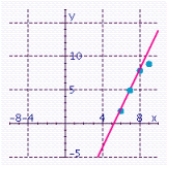
D) Estimated slope: 1.2; Estimated y-intercept: -1.5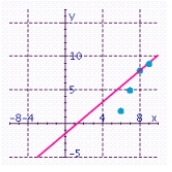
E) Estimated slope: 2.5; Estimated y-intercept: -16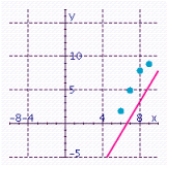
A) Estimated slope: 2; Estimated y-intercept: -12.5

B) Estimated slope: 2.5; Estimated y-intercept: -13

C) Estimated slope: 2.9; Estimated y-intercept: -15.3

D) Estimated slope: 1.2; Estimated y-intercept: -1.5

E) Estimated slope: 2.5; Estimated y-intercept: -16


Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
8
Sketch the graph of the function and specify all x- and y-intercepts. y =(x - 2) 2 + 4
A)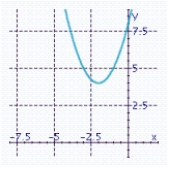 There is no x-intercept. y-intercept: 8
There is no x-intercept. y-intercept: 8
B)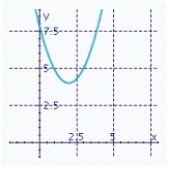 There is no x-intercept. y-intercept: 8
There is no x-intercept. y-intercept: 8
C)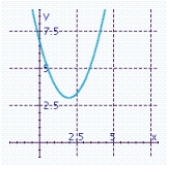 There is no x-intercept. y-intercept: 7
There is no x-intercept. y-intercept: 7
D)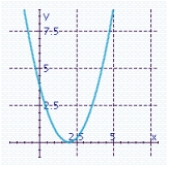 x-intercept: 0 y-intercept: 4
x-intercept: 0 y-intercept: 4
E)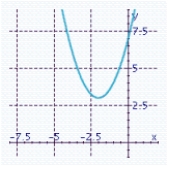 There is no x-intercept. y-intercept: 7
There is no x-intercept. y-intercept: 7
A)
 There is no x-intercept. y-intercept: 8
There is no x-intercept. y-intercept: 8B)
 There is no x-intercept. y-intercept: 8
There is no x-intercept. y-intercept: 8C)
 There is no x-intercept. y-intercept: 7
There is no x-intercept. y-intercept: 7D)
 x-intercept: 0 y-intercept: 4
x-intercept: 0 y-intercept: 4E)
 There is no x-intercept. y-intercept: 7
There is no x-intercept. y-intercept: 7
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
9
What is the largest possible area for a rectangle with a perimeter of 40 cm?
A) 400 cm 2
B) 100 cm 2
C) 90 cm 2
D) 130 cm 2
E) 150 cm 2
A) 400 cm 2
B) 100 cm 2
C) 90 cm 2
D) 130 cm 2
E) 150 cm 2

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
10
Find the linear function satisfying the given conditions. 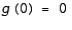 and
and 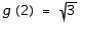
A)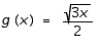
B)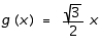
C)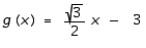
D)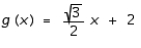
E)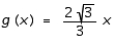
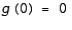 and
and 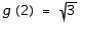
A)
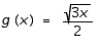
B)
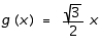
C)
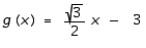
D)
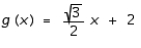
E)
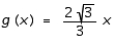

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
11
For the following figure, express the length AB as a function of x. (Hint: Note the similar triangles.) 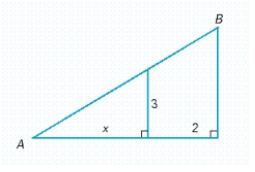
A)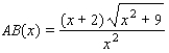
B)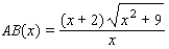
C)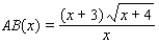
D)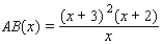
E)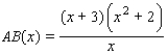

A)
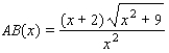
B)
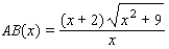
C)
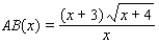
D)
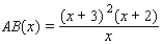
E)
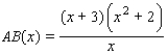

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
12
Find all fixed points of the function. 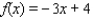
A) x = 1
B) x = - 1
C) x = 4
D) x = 3
E) no fixed points
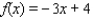
A) x = 1
B) x = - 1
C) x = 4
D) x = 3
E) no fixed points

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
13
A factory owner buys a new machine for $25,000. After eight years, the machine has a salvage value of $1,000. Find a formula for the value of the machine after t years, where 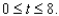
A) V (t) = - 3,000x + 25,000
B) V (t) = - 3,000x + 1,000
C) V (t) = 3,000x + 25,000
D) V (t) = 3,000x - 25,000
E) V (t) = - 3,000x - 25,000
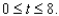
A) V (t) = - 3,000x + 25,000
B) V (t) = - 3,000x + 1,000
C) V (t) = 3,000x + 25,000
D) V (t) = 3,000x - 25,000
E) V (t) = - 3,000x - 25,000

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
14
Sketch the graph of the function and specify all x- and y-intercepts. y = (x - 2)(x - 1)(x + 1)
A)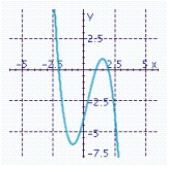 x-intercepts: - 2, 1, 2
x-intercepts: - 2, 1, 2
Y-intercept: -4
B)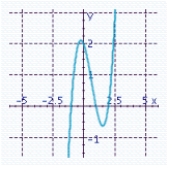 x-intercepts: - 1, 1, 2
x-intercepts: - 1, 1, 2
Y-intercept: 2
C)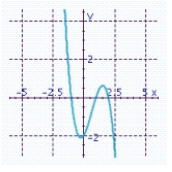 x-intercepts: - 1, 1, 2
x-intercepts: - 1, 1, 2
Y-intercept: -2
D)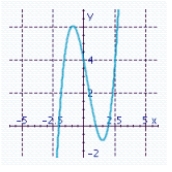 x-intercepts: - 2, 1, 2
x-intercepts: - 2, 1, 2
Y-intercept: 4
E)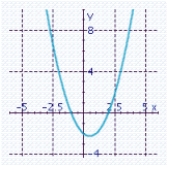 x-intercepts: - 1, 1
x-intercepts: - 1, 1
Y-intercepts: - 2.25
A)
 x-intercepts: - 2, 1, 2
x-intercepts: - 2, 1, 2Y-intercept: -4
B)
 x-intercepts: - 1, 1, 2
x-intercepts: - 1, 1, 2Y-intercept: 2
C)
 x-intercepts: - 1, 1, 2
x-intercepts: - 1, 1, 2Y-intercept: -2
D)
 x-intercepts: - 2, 1, 2
x-intercepts: - 2, 1, 2Y-intercept: 4
E)
 x-intercepts: - 1, 1
x-intercepts: - 1, 1Y-intercepts: - 2.25

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
15
Two points A and B move along the x-axis. After t sec, their positions are given by the equations 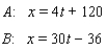 At what time t do A and B have the same x-coordinate?
At what time t do A and B have the same x-coordinate?
A) 7 sec
B) 6 sec
C) 5 sec
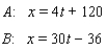 At what time t do A and B have the same x-coordinate?
At what time t do A and B have the same x-coordinate?A) 7 sec
B) 6 sec
C) 5 sec

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
16
Find all fixed points of the function. 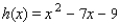
A) x = - 1, x = - 9
B) x = - 1, x = 9
C) x = - 9, x = 1
D) x = 9
E) no fixed points
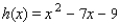
A) x = - 1, x = - 9
B) x = - 1, x = 9
C) x = - 9, x = 1
D) x = 9
E) no fixed points

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
17
Determine the input that produces the largest or smallest output (whichever is appropriate). State whether the output is largest or smallest. s = - 24t 2 + 147t + 15
A)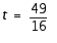 ; largest
; largest
B)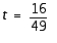 ; largest
; largest
C)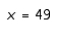 ; smallest
; smallest
D)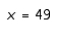 ; largest
; largest
E)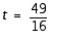 ; smallest
; smallest
A)
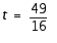 ; largest
; largestB)
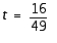 ; largest
; largestC)
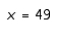 ; smallest
; smallestD)
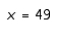 ; largest
; largestE)
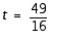 ; smallest
; smallest
Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
18
A piece of wire 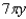 inches long is bent into a circle. Express the area of the circle as a function of y.
inches long is bent into a circle. Express the area of the circle as a function of y.
A)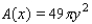
B)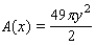
C)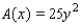
D)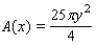
E)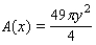
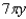 inches long is bent into a circle. Express the area of the circle as a function of y.
inches long is bent into a circle. Express the area of the circle as a function of y.A)
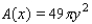
B)
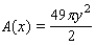
C)
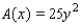
D)
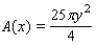
E)
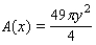

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
19
Suppose that the height of an object shot straight up is given by h =544t - 16t 2 . (Here h is in feet and t is in seconds.) Find the maximum height.
A) 4,724 ft
B) 4,624 ft
C) 1,156 ft
D) 4,290 ft
E) 5,189 ft
A) 4,724 ft
B) 4,624 ft
C) 1,156 ft
D) 4,290 ft
E) 5,189 ft

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
20
Among all rectangles having a perimeter of 24m, find the dimensions of the one with the largest area.
A)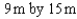
B)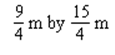
C)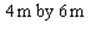
D)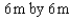
E)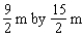
A)
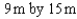
B)
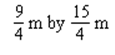
C)
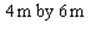
D)
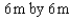
E)
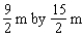

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
21
Sketch the graph of the rational function. Specify the intercepts and the asymptotes. 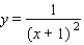
A) no x-intercepts; y-intercept: 1; no vertical asymptotes; horizontal asymptote: y = 0;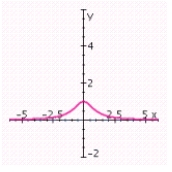
B) no x-intercepts; y-intercept: 1; vertical asymptote: x = 1; horizontal asymptote: y = 0;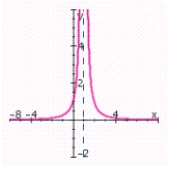
C) no x-intercepts; y-intercept: 1; vertical asymptote: x = - 1; horizontal asymptote: y = 0;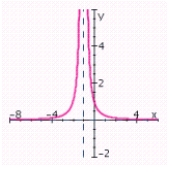
D) no x-intercepts; y-intercept: -1; vertical asymptote: x = 1; horizontal asymptote: y = 0;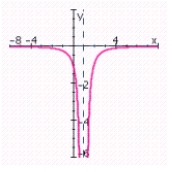
E) no x-intercepts; y-intercept: -1; no vertical asymptotes; horizontal asymptote: y = 0;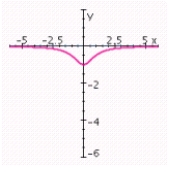
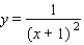
A) no x-intercepts; y-intercept: 1; no vertical asymptotes; horizontal asymptote: y = 0;

B) no x-intercepts; y-intercept: 1; vertical asymptote: x = 1; horizontal asymptote: y = 0;

C) no x-intercepts; y-intercept: 1; vertical asymptote: x = - 1; horizontal asymptote: y = 0;

D) no x-intercepts; y-intercept: -1; vertical asymptote: x = 1; horizontal asymptote: y = 0;

E) no x-intercepts; y-intercept: -1; no vertical asymptotes; horizontal asymptote: y = 0;


Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
22
Sketch the graph of the function and specify all x- and y-intercepts.y = x 3 - 9x
A)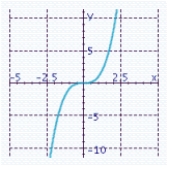 x-intercept: 0
x-intercept: 0
Y-intercept: 0
B)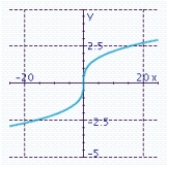 x-intercept: 0
x-intercept: 0
Y-intercept: 0
C)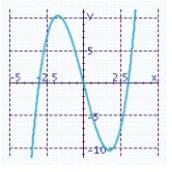 x-intercepts: -3, 0, 3
x-intercepts: -3, 0, 3
Y-intercept: 0
D)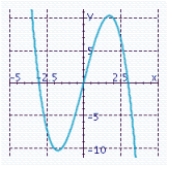 x-intercepts: -3, 0, 3
x-intercepts: -3, 0, 3
Y-intercept: 0
E)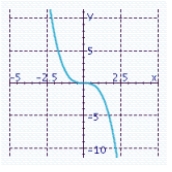 x-intercept: 0
x-intercept: 0
Y-intercept: 0
A)
 x-intercept: 0
x-intercept: 0Y-intercept: 0
B)
 x-intercept: 0
x-intercept: 0Y-intercept: 0
C)
 x-intercepts: -3, 0, 3
x-intercepts: -3, 0, 3Y-intercept: 0
D)
 x-intercepts: -3, 0, 3
x-intercepts: -3, 0, 3Y-intercept: 0
E)
 x-intercept: 0
x-intercept: 0Y-intercept: 0

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
23
Sketch the graph of the rational function. Specify the intercepts and the asymptotes. 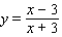
A) x-intercept: 3; y-intercept: - 1; vertical asymptote: x = - 3; horizontal asymptote: y = 1;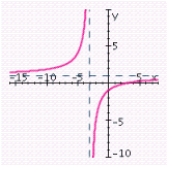
B) x-intercept: 0; y-intercept: - 1; vertical asymptote: x = 3; horizontal asymptote: y = - 1;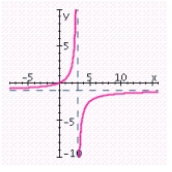
C) x-intercept: 3; y-intercept: 1; vertical asymptote: x = - 3; horizontal asymptote: y = - 1;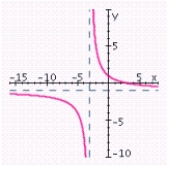
D) x-intercept: 3; y-intercept: - 1; vertical asymptote: x = 3; horizontal asymptote: y = - 1;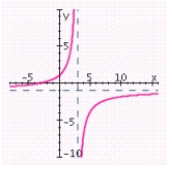
E) x-intercept: - 3; y-intercept: - 1; vertical asymptote: x = 3; horizontal asymptote: y = 1;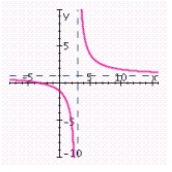
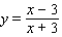
A) x-intercept: 3; y-intercept: - 1; vertical asymptote: x = - 3; horizontal asymptote: y = 1;

B) x-intercept: 0; y-intercept: - 1; vertical asymptote: x = 3; horizontal asymptote: y = - 1;

C) x-intercept: 3; y-intercept: 1; vertical asymptote: x = - 3; horizontal asymptote: y = - 1;

D) x-intercept: 3; y-intercept: - 1; vertical asymptote: x = 3; horizontal asymptote: y = - 1;

E) x-intercept: - 3; y-intercept: - 1; vertical asymptote: x = 3; horizontal asymptote: y = 1;


Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
24
Sketch the graph of the function and specify all x- and y-intercepts. y = x 3 (x + 1)
A)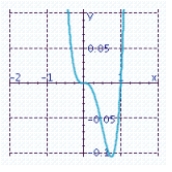 x-intercepts: 0, 1
x-intercepts: 0, 1
Y-intercept: 0
B)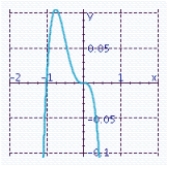 x-intercepts: 0, - 1
x-intercepts: 0, - 1
Y-intercept: 0
C)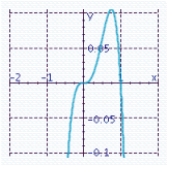 x-intercepts: 0, 1
x-intercepts: 0, 1
Y-intercept: 0
D)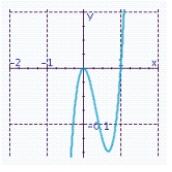 x-intercepts: 0, 1
x-intercepts: 0, 1
Y-intercept: 0
E)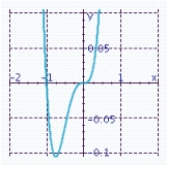 x-intercepts: 0, - 1
x-intercepts: 0, - 1
Y-intercept: 0
A)
 x-intercepts: 0, 1
x-intercepts: 0, 1Y-intercept: 0
B)
 x-intercepts: 0, - 1
x-intercepts: 0, - 1Y-intercept: 0
C)
 x-intercepts: 0, 1
x-intercepts: 0, 1Y-intercept: 0
D)
 x-intercepts: 0, 1
x-intercepts: 0, 1Y-intercept: 0
E)
 x-intercepts: 0, - 1
x-intercepts: 0, - 1Y-intercept: 0

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck
25
Sketch the graph of the rational function. Specify the intercepts and the asymptotes. 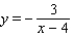
A) no x-intercepts; y-intercept: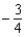 ; vertical asymptote: x = - 4; horizontal asymptote: y = 0;
; vertical asymptote: x = - 4; horizontal asymptote: y = 0; 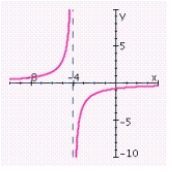
B) no x-intercepts; y-intercept: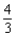 ; vertical asymptote: x = 4; horizontal asymptote: y = 0;
; vertical asymptote: x = 4; horizontal asymptote: y = 0; 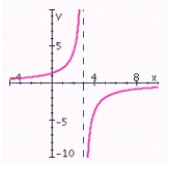
C) no x-intercepts; y-intercept: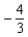 ; vertical asymptote: x = 4; horizontal asymptote: y = 0;
; vertical asymptote: x = 4; horizontal asymptote: y = 0; 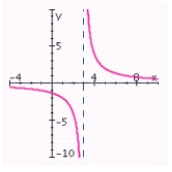
D) no x-intercepts; y-intercept: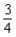 ; vertical asymptote: x = 4; horizontal asymptote: y = 0;
; vertical asymptote: x = 4; horizontal asymptote: y = 0; 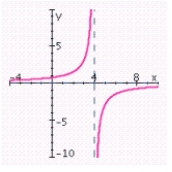
E) no x-intercepts; y-intercept: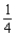 ; vertical asymptote: x = 4; horizontal asymptote: y = 0;
; vertical asymptote: x = 4; horizontal asymptote: y = 0; 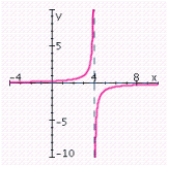
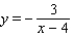
A) no x-intercepts; y-intercept:
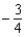 ; vertical asymptote: x = - 4; horizontal asymptote: y = 0;
; vertical asymptote: x = - 4; horizontal asymptote: y = 0; 
B) no x-intercepts; y-intercept:
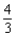 ; vertical asymptote: x = 4; horizontal asymptote: y = 0;
; vertical asymptote: x = 4; horizontal asymptote: y = 0; 
C) no x-intercepts; y-intercept:
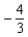 ; vertical asymptote: x = 4; horizontal asymptote: y = 0;
; vertical asymptote: x = 4; horizontal asymptote: y = 0; 
D) no x-intercepts; y-intercept:
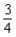 ; vertical asymptote: x = 4; horizontal asymptote: y = 0;
; vertical asymptote: x = 4; horizontal asymptote: y = 0; 
E) no x-intercepts; y-intercept:
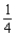 ; vertical asymptote: x = 4; horizontal asymptote: y = 0;
; vertical asymptote: x = 4; horizontal asymptote: y = 0; 

Unlock Deck
Unlock for access to all 25 flashcards in this deck.
Unlock Deck
k this deck


